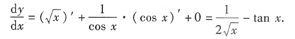一、选择题9. 设函数
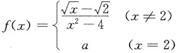
，在x=2处连续，则a=
A．
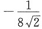
B．
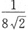
C．
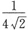
D．
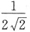
A B C D
B
[解析] 因为
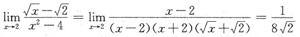
二、填空题1. 若f(x)在x=a处可导，则
=______.
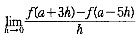
8f'(a)
[解析] ∵f(x)在x=a处可导
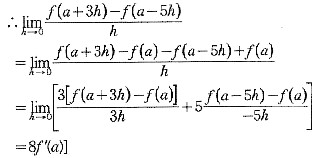
2. 设f(x)=ln(1+x
2)，则f"(-1)=______.
3.
4. 设f(x)二阶可导，y=e
f(x)，则y''=______.
[解析]
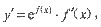
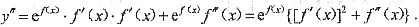
5.
7.
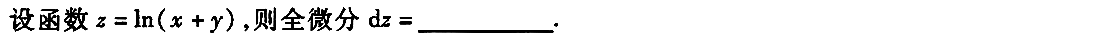
8. 曲线y=ln(x+1)的渐近线为______。
9.
10. 设
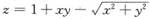
，则
=______．
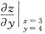
[解析] ∵
，
∴
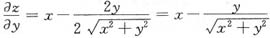
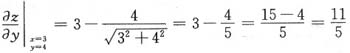
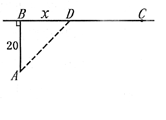
三、解答题1. 如图7-1，工厂A到铁路线的垂直距离为20km，垂足为且铁路线上的C是距B处100km的原材料供应站．现要在BC之间的D处向工厂A修一条公路，使得从材料供应站C经D到工厂A所需要的运费最省，问D应选在何处?
(已知1 km的铁路运费与公路运费之比是3:5．)
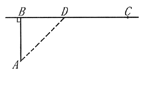
本题考查的知识点是利用导数研究函数特性的方法．
[解析] 本题的关键是正确列出函数的关系式，再求其极小值．
解 如图7-2，设BD=x，铁路的运费为30元/km，总运费为了元．根据题意，有
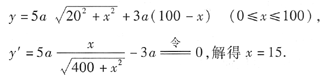
由于只有唯一的驻点，依题意x=15为所求．
答：D点应修建在距B处15km处．
注意 若设铁路的运费为1个单位(元)/km，则在题目中不会出现常数a
2.
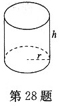
3. 某工厂要制造一个无盖的圆柱形发酵池，其容积是
，池底的材料30元/m
2，池壁的材料20元/m
2，问如何设计，才能使成本最低，最低成本是多少元?
设池底半径为r，池高为h(如图所示)，则
，得
．
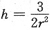
又设制造成本为S，则
S=30·πr
2+20·27πrh
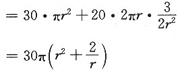
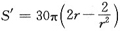
令S'=0，得驻点r=1．
因为
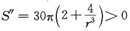
所以r=1为唯一的极小值，即为最小值点．
所以，池底半径为1m，高为
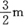
时，可使成本最低，最低成本为90π元．
[解析] 本题考查的知识点是应用导数求实际问题的极值．所谓“成本最低”，即求制造成本函数在已知条件下的最小值．因此，本题的关键是正确写出制造成本函数的表达式，再利用已知条件将其化为一元函数，并求其极值．
4. 设f(x)是(-∞，+∞)内连续的偶函数．
证明：
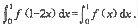
证：设
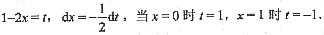
则
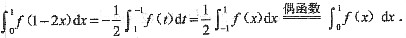
5.
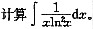
6.
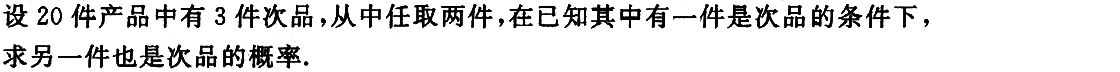
7. 设事件A与B相互独立，且P(A)=0.6，P(B)=0.7，求P(A+B)．
本题考查事件相互独立的概念及加法公式．
[解析] 若事件A与B相互独立，则P(AB)=P(A)P(B)．
8.
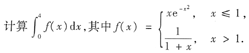
本题考查的知识点是复合函数的求导．
解
即
所以
D．
，则f(x)在点x=0处 
，当x→0时，y'→+∞．
深色：已答题 浅色：未答题