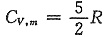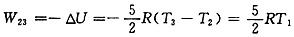一、单项选择题(在每小题列出的四个备选项中只有一个是符合题目要求的。)
1. 有两种气体,它们的分子数密度不同,但它们的分子平均平动动能相同,则两种气体的温度和压强______。
- A.相同 不相同
- B.不相同 不相同
- C.相同 相同
- D.不相同 相同
A B C D
A
[考点] 本题主要考查的知识点为理想气体的温度和压强公式。
根据理想气体的温度公式:

=

,已知两种气体的平均平动动能

相同,可判断两种气体的温度T也相同;而根据理想气体的压强公式

,已知

相同,而分子数密度n不同,所以两者压强不同。
5. 一定量的某种单原子分子理想气体在等压过程中对外做功为200J,若为双原子分子气体,则需吸收的热量为______。
A B C D
A
[考点] 本题相近的考点在2009年10月真题第二大题第24小题考查过,主要考查的知识点为等压过程的特征和简单应用以及比热容比的概念。
在等压过程中,W
p=νR△T=200J吸收的热量Q
p=νC
p,m△T,

,当气体为双原予分子时i=5,
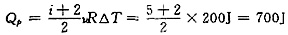
。
10. 若室内生起炉子后温度从15℃上升到27℃,而室内的气压不变,则此时室内的分子数减少了______。
A B C D
B
[考点] 本题主要考查的知识点为理想气体物态方程的应用。
由于

,由题意可知两个温度下pV不变,所以

,即m
1T
1=m
2T
2,将数值代入得


,从而得m
2=0.96m
1,所以分子数减少了4%。
二、填空题(请在每小题的空格中填上正确答案。)
1. 一容器内贮有氢气,其压强p=2.00×10
5Pa,分子密度n=4.83×10
25个/m
3,则气体的温度为______。
300K
[考点] 本题主要考查的知识点为理想气体的压强和温度公式。

,所以

=(3×2×10
5)÷(2×4.83×10
25)=6.21×10
-21J

,所以T=

=(2×6.21×10
-21)÷(3×1.38×10
-23)=300K
2. 理想气体体积为V,压强为p,温度为T,一个分子的质量为m,k为玻尔兹曼常数,R为摩尔气体常量,则该理想气体的分子总数为______。
[考点] 本题相近的考点在2009年10月真题第二大题第23小题考查过,主要考查的知识点为理想气体的物态方程和R,k之间的关系。
理想气体物态方程的一般形式pV=νRT,由波尔兹曼常数的定义

,代入上式得,pV=νN
AkT=NkT,N为气体的分子总数,所以

。
3. 气体经历如图所示的循环过程。在一次循环中,气体对外所做的净功是______。
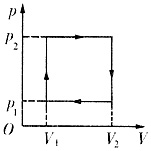
(p2-p1)(V2-V1)
[考点] 本题在2009年4月真题第二大题第24小题考查过,主要考查的知识点为p-V图的应用。
气体对外所做的净功即为以(p2-p1)为宽。(V2-V1)为长的矩形的面积,即气体对外所做功为(p2-p1)(V2-V1)。
4. 温度为T的1mol双原子分子理想气体的热力学能为(摩尔气体常数用R表示)______。
[考点] 本题在2010年4月真题第二大题第23小题考查过,主要考查的知识点是热力学能公式。
由理想气体热力学能公式U=

且v=1,可得

。
5. 氮气液化的过程中,把氮气放在一个绝热的汽缸中。开始时,氮气的压强为50个标准大气压,温度为300K;经急速膨胀后,其压强降至1个标准大气压,从而氮气被液化,此时氮气的温度为______。
98K
[考点] 本题相近的考点在2008年10月真题第二大题第24小题考查过,主要考查的知识点为理想气体绝热过程的计算。
6. 某理想气体分子在温度T
1和T
2时的麦克斯韦速率分布曲线如图所示,两温度下相应的分子平均速率分别为

和

,则T
1______T
2,

______

。(填大于、小于或等于)

小于 小于
[考点] 本题在2009年4月真题第一大题第6小题考查过,主要考查的知识点为麦克斯韦速率分布曲线的物理意义。
由图可知,T
1<T
2,而当温度升高时气体分子热运动加剧,故

,也可直接由图上T
2线明显比T
1线偏右,即分子速率整体上要大于1。
三、计算题(要写出主要的解题过程。)
1. 现有理想气体,压强为1Pa,温度为200K,则:
(1)在1000升中有多少个气体分子?
(2)这些分子的平动动能是多少?
(1)由p=nkT

(2)由

=

×1.38×10
-23×200
=4.14×10
-21J
则在1000升中所有分子的平动动能是
E=

=3.62×10
20×4.14×10
-21=1.499J。
2. 一容积为11.2×10
-3m
3的真空系统已被抽到1.3158×10
-3Pa的真空,为了提高其真空度,将它放在300℃的烘箱内烘烤,使器壁释放出吸附的气体分子,若烘烤后压强增加为1.3158Pa,那么器壁上原来吸附了多少个分子?
由公式p=nkT得:

分子总数N=nV=1.66×10
20×11.2×10
-3 =1.86×10
18个
3. 一定量的氢气在保持压强为4×10
5Pa不变的情况下,温度由0℃升高到50℃,吸收了6×10
4J的热量,求:
(1)氢气的摩尔数是多少?
(2)氢气内能改变了多少?
(3)氢气对外做了多少功?
(4)如果氢气的体积不变而温度发生同样变化,则它该吸收多少热量?
(1)由等压过程Q
p=νC
p,m(T
2-T
1)
可得

(2)△U=νC
V,m(T
2-T
1)=41.3×

×8.31×50
=4.29×10
4J
(3)W
p=Q
p-△U=6×10
4-4.29×10
4 =1.71×10
4J
(4)因为是等体变化,即W=0
所以Q=△U=4.29×10
4J。
4. 已知热机在一次循环中,工作物质向低温热源放热Q
2是热机对外做功W的4倍,则
(1)经一次循环过程,工作物质从高温热源吸热Q
1为W的多少倍?
(2)求热机效率η。
(1)热机吸热Q
1=Q
2+W=5W则

。
(2)热机效率

。
四、分析计算题(要写出解题所依据的定理、定律、公式或相应的分析图。)
1. 1mol双原子(刚性)分子的理想气体,作如图所示的可逆正循环,其中1→2为直线,2→3为绝热线,3→1为等温线,已知T
2=2T
1,V
3=8V
1。试求:2→3过程,气体对外做的功;系统的内能增量和系统传递的热量(计算结果用T
1和已知常数表示)。

因为是刚性双原子分子理想气体
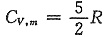
2→3过程中,因为是绝热过程,所以气体对外做功
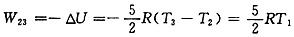
注意T
3=T
1 T
2=2T
1 系统的内能增量

系统传递的热量Q
23=W
23+△U=0。
 =
= ,已知两种气体的平均平动动能
,已知两种气体的平均平动动能 相同,可判断两种气体的温度T也相同;而根据理想气体的压强公式
相同,可判断两种气体的温度T也相同;而根据理想气体的压强公式 ,已知
,已知 相同,而分子数密度n不同,所以两者压强不同。
相同,而分子数密度n不同,所以两者压强不同。 ,当气体为双原予分子时i=5,
,当气体为双原予分子时i=5,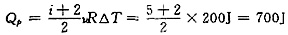 。
。
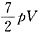
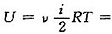
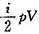 ,得U=3pV。
,得U=3pV。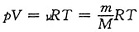
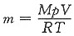
 ,由题意可知两个温度下pV不变,所以
,由题意可知两个温度下pV不变,所以 ,即m1T1=m2T2,将数值代入得
,即m1T1=m2T2,将数值代入得
 ,从而得m2=0.96m1,所以分子数减少了4%。
,从而得m2=0.96m1,所以分子数减少了4%。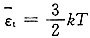 可知,只要温度相同,它们的分子平均平动动能就相同,而两种气体分子的平均能量、平均动能、内能未必相等,故D项正确。
可知,只要温度相同,它们的分子平均平动动能就相同,而两种气体分子的平均能量、平均动能、内能未必相等,故D项正确。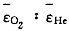 为(已知氧原子量为16,氦原子量为4)______。
为(已知氧原子量为16,氦原子量为4)______。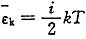 ,氧气i=5氨气i=3,所以
,氧气i=5氨气i=3,所以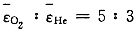 。
。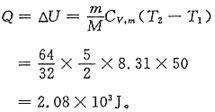
 ,所以
,所以 =(3×2×105)÷(2×4.83×1025)=6.21×10-21J
=(3×2×105)÷(2×4.83×1025)=6.21×10-21J ,所以T=
,所以T= =(2×6.21×10-21)÷(3×1.38×10-23)=300K
=(2×6.21×10-21)÷(3×1.38×10-23)=300K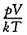
 ,代入上式得,pV=νNAkT=NkT,N为气体的分子总数,所以
,代入上式得,pV=νNAkT=NkT,N为气体的分子总数,所以 。
。
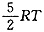
 且v=1,可得
且v=1,可得 。
。 和
和 ,则T1______T2,
,则T1______T2, ______
______ 。(填大于、小于或等于)
。(填大于、小于或等于)
 ,也可直接由图上T2线明显比T1线偏右,即分子速率整体上要大于1。
,也可直接由图上T2线明显比T1线偏右,即分子速率整体上要大于1。

 ×1.38×10-23×200
×1.38×10-23×200 =3.62×1020×4.14×10-21=1.499J。
=3.62×1020×4.14×10-21=1.499J。

 ×8.31×50
×8.31×50 。
。 。
。