一、单项选择题(在每小题列出的四个备选项中只有一个是符合题目要求的。)
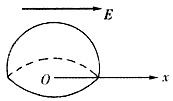
1. 一电场强度为E的均匀电场,E的方向与x轴正向平行,如图所示,则通过图中一半径为R的半球面的电场强度通量为______。
A.πR
2E B.
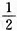
πR
2E
C.2πR
2E D.0
A B C D
D
[考点] 本题主要考查的知识点为对电场强度通量的理解,也可用高斯定理。
因题图所示,穿入和穿出半球面的电场线的条数相等,所以通过半球面的电场强度通量为零。
4. 长宽分别为a和b的矩形线框置于均匀磁场B中,磁场随时间变化的规律为B=B
0sin(ωt),将线圈平面与磁场方向垂直,则此感应电动势的大小为______。
- A.abωB0cos(ωt)
- B.abωB0sin(ωt)
- C.-abωB0sin(ωt)
- D.-abωB0cos(ωt)
A B C D
D
[考点] 本题主要考查的知识点为法拉第电磁感应定律的应用。
由穿过线圈的磁通量为Φ
m=
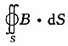
=abB
0sin(ωt),则
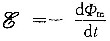
=-abωB
0cos(ωt)。
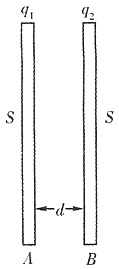
5. 如图所示,真空中两块面积均为S的平板A和B彼此平行放置,板间距离为d,d远小于板的线度。设A,B板都均匀带正电,电量分别为q
1和q
2,则A、B两板间的电势差为______。
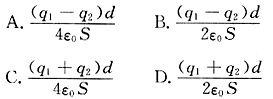
A B C D
B
[考点] 本题主要考查的知识点为对电势差的定义的应用。
设A、B两板的电荷面密度分别为则两极板间的场强
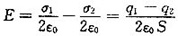
,两极板间的电势差为
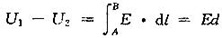
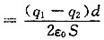
。
7. 边长为0.2m的正方形线圈,共有50匝,线圈上通一电流2A,并把线圈放在磁感应强度为0.05T的均匀磁场中,则线圈所受的最大磁力矩M______。
- A.0.1N·m
- B.0.2N·m
- C.0.4N·m
- D.0.6N·m
A B C D
B
[考点] 本题主要考查的知识点为磁场对平面载流线圈的作用磁力矩的计算。
由M=NBISsinθ,当
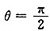
时,
M=M
max=NBIS
=50×0.05×2×(0.2)
2N·m
=0.2N·m。
8. 当自感为2H的线圈通以10A的电流的时候,线圈中储存的磁场能为______。
A B C D
C
[考点] 本题主要考查的知识点为载流线圈的磁场能。线圈中储存的磁场能W
m=
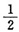
LI
2=
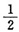
×2×10
2J=100J
15. 无限长直圆柱体,半径为R,沿轴向通有均匀电流,设圆柱体内(r<R)的磁感应强度大小为B
i,圆柱体外(r>R)的磁感应强度大小为B
e,则有______。
- A.Bi、Be均与r成正比
- B.Bi、Be均与r成反比
- C.Bi与,一成反比,Be与r成正比
- D.Bi与r成正比,Be与r成反比
A B C D
D
[考点] 本题主要考查的知识点为磁场的安培环路定理。
对圆柱体外任意一点,r>R,路径L包围了整个电流,根据安培环路定理B·2πr=μ
0I
得
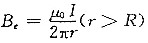
。
对圆柱体内任意一点,r<R,根据安培环路定理
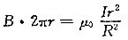
得
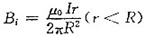
。
18. 在匀强磁场中,放置有面积为S的可绕轴转动的N匝线圈,若线圈以角速度ω作匀速转动,则线圈中的感应电动势为______。
A.NBSωcos(ωt) B.NBSsin(ωt)
C.NBScos(ωt)D.NBSωsin(ωt)
A B C D
D
[考点] 本题主要考查的知识点为法拉第电场感应定律的简单计算。
设t=0时,线圈平面与磁场垂直。经过时间t,线圈平面转过角度θ,
则θ=ωt
Ψ=NΦ
m=NBScos(ωt)

。
二、填空题(请在每小题的空格中填上正确答案。)
1. 如图所示,无限长直导线在P处弯成半径为R的圆,当通以电流I时,则导线在圆心O点产生的磁感应强度大小等于______。
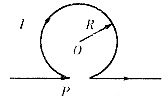
[考点] 本题主要考查的知识点为对磁场的公式的理解及磁场的叠加。
磁场的叠加问题,圆导线在O点产生的磁感应强度为
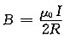
,无限长直导线对O点产生的磁感应强度为
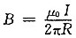
,将两者叠加,但要注意两者方向相反的问题。
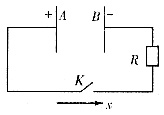
2. 如图所示为一充电后的平行板电容器,A板带正电,B板带负电,当将开关K合上时,A、B板之间的电场方向为______。(设图上所标的方向为x轴正方向)
3. 如图所示,3根长直载流导线1,2,3平行且共面,分别载有稳恒电流I,2I,3I,导线1和3的距离为d,欲使导线2受力为零,则导线2与1的距离应为______。
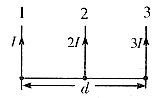
d/4
[考点] 本题主要考查的知识点为磁感应强度的计算。
设导线1和导线2之间的距离为a,由图可知,导线1在导线2上任一点处产生的磁感应强度
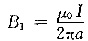
,方向垂直纸面向里;导线3出导线2上任一点处产生的磁感应强度B
2=
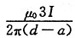
,方向垂直纸面向外。根据题意可知,B
1=B
2,则
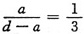
,可得

。
4. 产生感生电动势的非静电力是______;产生动生电动势的非静电力是______。
5. 在一个不带电的金属球壳的球心放一个点电荷q>0,将此点电荷偏离球心,该金属壳的电势将______。
6. 自感为0.25H的线圈中,当电流在(1/16)s内由2A均匀减小到零时,线圈中的自感电动势为______。
8V
[考点] 本题主要考查的知识点为自感的简单计算。
由自感电动势公式可得,

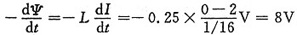
。
三、计算题(要写出主要的解题过程。)
1. 如图所示,一均匀磁场的磁感应强度B=0.01T,一动能为20eV的正电子以与磁场成60°角的方向射入,求该正电子周期T、半径R和运动轨迹螺旋线的螺距h。(已知电子的质量m=9.1×10
-31kg,电子电量q=1.6×10
-19C,1eV=1.602×10
-19J)
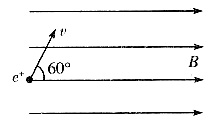
已知正电子动能为20eV=3.2×10
-18J
所以
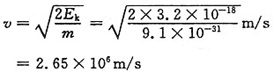
正电子做螺旋运动的周期

螺距h=Tvcosθ
=3.57×10
-9×2.65×10
6×
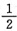
m
=4.73×10
-3m
螺旋线的半径
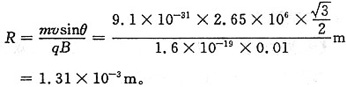
2. 如图所示,长直导线内通有电流I,与其相距r
0处有一直角三角形线圈ABC,已知BC=a,CA=b,设线圈以速度v向右运动,试求线圈内的感应电动势。
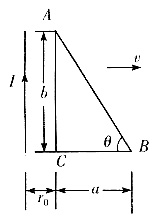
对AC来说,因B、V、I三者相互垂直,AC边上各点的磁感应强度相等,所以AC边的动生电动势为
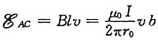
,电动势的方向由C指向A;由于CB边不切割磁感线,所以

;对于BA边来说,导线上各点的磁感应强度不等,且v和I方向不垂直,在BA边上任取dl,其动生电动势为
d
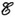
=(v×B)dl=-Bvsinθdl
BA边上的动生电动势
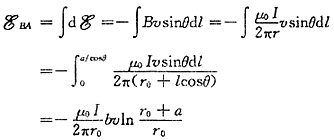
根据右手定则知
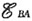
方向由B指向A
三角形线圈的总电动势为
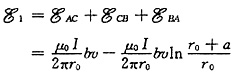
。
3. 如图所示,导体棒AB与金属轨道CA和DB接触,整个线框放在B=0.5T的均匀磁场中,磁场方向与纸面垂直。
(1)若导体棒以4m/s的速度向右运动,求棒内产生的感应电动势;
(2)若导体棒运动到某一位置时,电路的电阻为0.2Ω,求此时棒所受的力。
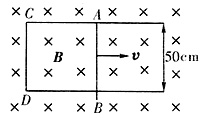
磁感应强度B=0.5T
AB棒的长度l=50cm=0.5m
(1)速度v=4m/s
dΦ
m=B·dS=Bldx
由法拉第电磁感应定律得
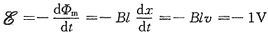
。
(2)R=0.2Ω,电路中的电流强度
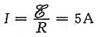
棒所受的力
F=BIl=0.5×5×0.5=1.25N。
四、分析计算题(要写出解题所依据的定理、定律、公式或相应的分析图。)
1. 如图,一半径为R
1的导体球A与内、外半径分别为R
2和R
3的导体球壳B同心放置,A带电量为q,B带电量为q'。求:
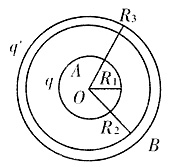
(1)说明球壳B内表面带电量为-q的依据;
(2)导体球壳B外表面的带电量为多少?
(3)求A与B之间的电场强度大小的分布与电势差;
(4)计算A与B形成的球形电容器的电容。
(1)根据静电平衡条件,导体达到静电平衡时导体内部场强为零。在导体球壳B内作高斯面,由高斯定理可得导体球A所带电量与导体球壳B内表面所带电量之和为零。因此在导体球壳B内表面带电量为-q。
(需要强调写出的关键信息:导体达到静电平衡时导体内部场强为零、高斯定理)
(2)由电荷守恒定律,外表面带电q'+q。
(3)由高斯定理
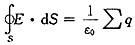
得场强分布
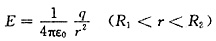
电势差
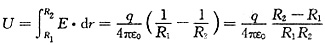
。
(4)电容
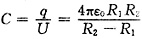
。

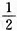 πR2E
πR2E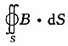 =abB0sin(ωt),则
=abB0sin(ωt),则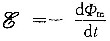 =-abωB0cos(ωt)。
=-abωB0cos(ωt)。
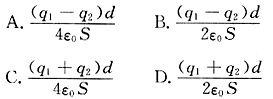
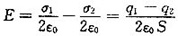 ,两极板间的电势差为
,两极板间的电势差为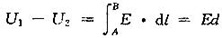
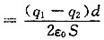 。
。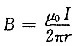 ,从而随着S移近长导线,B增大。
,从而随着S移近长导线,B增大。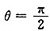 时,
时,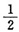 LI2=
LI2=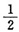 ×2×102J=100J
×2×102J=100J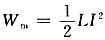 ,则它______。
,则它______。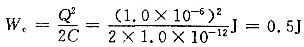
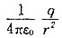 得
得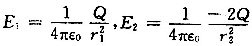 ,要使P点的电场强度为零,即两电荷在P点产生的电场强度矢量和为0,则P点应在z轴上x<0处。
,要使P点的电场强度为零,即两电荷在P点产生的电场强度矢量和为0,则P点应在z轴上x<0处。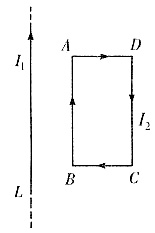
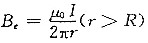 。
。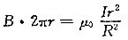
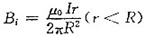 。
。 。
。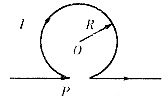

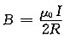 ,无限长直导线对O点产生的磁感应强度为
,无限长直导线对O点产生的磁感应强度为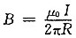 ,将两者叠加,但要注意两者方向相反的问题。
,将两者叠加,但要注意两者方向相反的问题。

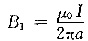 ,方向垂直纸面向里;导线3出导线2上任一点处产生的磁感应强度B2=
,方向垂直纸面向里;导线3出导线2上任一点处产生的磁感应强度B2=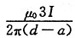 ,方向垂直纸面向外。根据题意可知,B1=B2,则
,方向垂直纸面向外。根据题意可知,B1=B2,则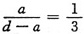 ,可得
,可得 。
。
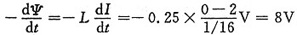 。
。
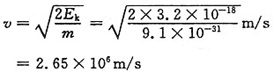

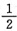 m
m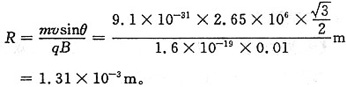

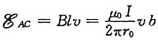 ,电动势的方向由C指向A;由于CB边不切割磁感线,所以
,电动势的方向由C指向A;由于CB边不切割磁感线,所以 ;对于BA边来说,导线上各点的磁感应强度不等,且v和I方向不垂直,在BA边上任取dl,其动生电动势为
;对于BA边来说,导线上各点的磁感应强度不等,且v和I方向不垂直,在BA边上任取dl,其动生电动势为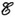 =(v×B)dl=-Bvsinθdl
=(v×B)dl=-Bvsinθdl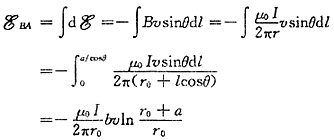
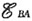 方向由B指向A
方向由B指向A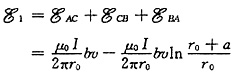 。
。
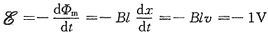 。
。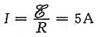 棒所受的力
棒所受的力
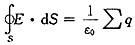
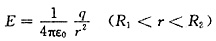
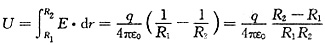 。
。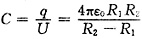 。
。