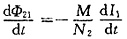一、单项选择题(在每小题列出的四个备选项中只有一个是符合题目要求的。)
1. 一质点的运动方程是r=Rcos(ωt)i+Rsin(ωt)j,其中R,ω为正值常数,从t=π/ω到t=2π/ω的时间内,该质点的位移是______。
A B C D
B
[考点] 本题相近的考点在2008年4月第二大题第22小题考查过,主要考查的知识点为位移的概念。
将t的值代入r=Rcos(ωt)i+Rsin(ωt)j,当t=π/ω时,

=Rcosπi+Rsinπj=-Ri
当t=2π/ω时,

=Rcos(2π)i+Rsin(2π)j=Ri
r=r
2-r
1=2Ri。
3. 质量分别为m和m
0的滑块A和B,叠放在光滑水平桌面上,如图所示。A和B间的静摩擦因数为μ
s,动摩擦因数为μ,系统原处于静止状态。今有一水平力F作用于A上,若要使A相对于B滑动,则应有______。

A.F≥μ
s,mg B.F≥μ
s(m+m
0)g

A B C D
C
[考点] 本题相近考点在2008年10月真题第二大题第22小题考查过,主要考查的知识点为静摩擦力和滑动摩擦力以及牛顿第二定律的应用。
进行受力分析
对A物体:F-f=ma
A 对B物体:f=m
0a
B 因为滑动摩擦力f≤μ
smg
所以对于物体B,

所以对于物体A,


所以若要使B相对于A相对滑动,则F≥F
max=

。
5. 如图所示,有三个质量相同的质点a、b、c,带有等量的正电荷,它们从相同的高度自由下落,在下落过程中带电质点b、c分别进入如图所示的匀强电场与匀强磁场中,设它们落到同一水平面的动能分别为E
a、E
b、E
c,则______。

- A.Ea<Eb=Ec
- B.Ea=Eb=Ec
- C.Eb>Ea=Ec
- D.Eb>Ec>Ea
A B C D
C
[考点] 本题主要考查的知识点为电场和磁场对电荷做功。
设运行的高度为h
E
a=mgh
则E
b=qU
E
c=

mv
2 经分析,知E
b>E
a=E
c。
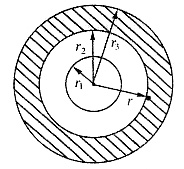
9. 如图所示,一螺线管铅直放置并通有直流电流,螺线管正上方有一导体圆环,沿螺线管轴线铅直下落,假设下落过程中圆环面恒保持水平,则圆环经图A、B、C三点时的加速度大小应满足______。

- A.aA<aB<aC
- B.aA<aC<aB
- C.aC<aA<aB
- D.aB<aA<aC
A B C D
C
[考点] 本题主要考查的知识点为牛顿第二定律和磁力的结合。
分析圆环在A、B、C三点的受力,依题意有
mg-f
A=ma
A,mg=ma
B,mg-f
C=ma
C 圆环速度v
C>v
A,故

。磁力f
C>f
A,因而a
C<a
A<a
B。
10. 已知有同方向的两简谐振动,它们的运动方程分别为x
1=5cos(10t+0.75π)cm,x
2=6cos(10t+0.25π)cm,则合振动的振幅为______。
A.

B.
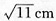
C.11cm D.61cm
A B C D
A
[考点] 本题主要考查的知识点为合振动的振幅的计算方法。
合振动的振幅
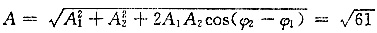
。
14. 波长为λ=450nm的单色光垂直入射到光栅常数d=2×10
-4cm的平面衍射光栅上,可能观察到的光谱线的最大级次为______。
A B C D
C
[考点] 本题主要考查的知识点为光栅衍射公式的应用。
根据光栅衍射公式
dsinθ=±kλ
当θ为π/2时,为最大级次,即
d=±kλ

。
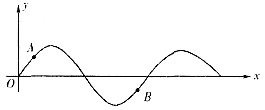
15. 某时刻一简谐波的波形如图所示,则a、b两点间的相位差为______。

A.π B.

C.0 D.

A B C D
B
[考点] 本题主要考查的知识点为简谐波上不同点的相位差的计算。
由公式

可得a、b两点间的相位差为

。
二、填空题(请在每小题的空格中填上正确答案。)
1. 某车的速度v和时间t的关系为

,当车的速率减小到4km/h时,车走过的路程为______。
32.19km
[考点] 本题考点在2009年10月真题第二大题第22小题考查过,主要考查的知识点为运动学第二类问题知v求r。
根据公式

则dr=vdt,

2. 质量为m的人造卫星沿一圆形轨道运动,地球半径为R,卫星距离地面的高度为2R,地球的质量为M,则卫星的动能为______。
[考点] 本题考点在2010年4月真题第一大题第5小题考查过,主要考查的知识点为万有引力提供向心力的相关计算。
卫星受到的引力为向心力
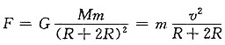

3. 温度为T的刚性单原子分子理想气体有N个分子,该气体的热力学能U=______。(玻尔兹曼常数为k)
[考点] 本题在2008年10月真题第二大题第23小题考查过,主要考查的知识点为热力学能公式和常量k和R的关系。
由理想气体热力学能公式,对于单原子分子,

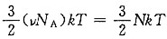
。
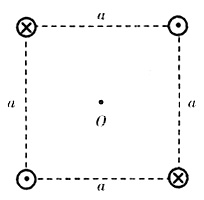
4. 在真空中有半径为R的一根半圆形导线,流过的电流为I,则圆心处的磁感应强度为______。
[考点] 本题考点在2009年10月真题第一大题第9小题考查过,主要考查的知识点为特殊磁场的磁场强度公式。
由公式

,在半圆内dl=rdθ,则
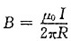
。
5. 半径分别为R和r的两个球形导体,用很长的导线将它们连起来,使两导体带电,电势为U,则两球表面电荷密度之比为______。
[考点] 本题考点在2008年4月真题第二大题第25小题考查过,主要考查的知识点为等势体的概念。
因为两球相距较远,不会影响各由的电荷分布。两球连接,电势应该相等,所以

所以σ
小球:σ
大球=R:r。
6. 一飞船的静止长度为120m,若该飞船以0.8c的速度相对于地面匀速飞行时,在地面上测得该飞船的长度为______。
72m
[考点] 本题在2009年10月真题第2大题第26小题考查过,主要考查的知识点为相对论的时空观中的长度缩短效应。

三、计算题(要写出主要的解题过程。)
1. 一定量的理想气体,压强为p
1,温度为了T
1,与同体积的压强为p
2,温度为T
2的同种理想气体相混合,已知混合后气体的体积为原来气体体积之和,在混合过程中与外界没有发生能量交换,求混合后气体的温度和压强。
混合前气体的物质的量等于混合后气体的物质的量,由pV=νRT可得
混合前

混合后

有

(1)
又因为混合过程中与外界未发生能量交换,内部又没有发生化学反应,故混合前后的气体的内能相等,由E=νC
V,m可得
ν
1C
V,mT
1+ν
2C
V,mT
2=(ν
1+ν
2)C
V,mT

(2)
综合(1)、(2)可得混合后气体的温度为

可得混合气体的压强为p=

(p
1+p
2)。
2. 质量都为M的两个冰车同时静止在光滑的水平冰面上,一质量为m的人从第一个冰车跳到第二个冰车上,再由第二个冰车跳回到第一个冰车,求两个冰车的末速度之比。
以两冰车和人为研究对象,因为冰面光滑,系统在水平方向上不受外力,故动量守恒。若人以对地的速度u水平跳出,以向右方向为正方向,人从第一辆冰车跳出,第一辆冰车获得速度v
1,有
mu+Mv
1=0

人跳到第二个冰车,第二个冰车获得速度v
2,有
mu=(M+m)v
2 
人从第二个冰车上跳出,第二个冰车获得速度v'
2 (m+M)v
2=-mu+Mv'
2 
人跳回第一个冰车,第一个冰车获得速度v'
1-mu+Mv
1=(m+M)v'
1 
3. 平行放置两偏振片,使它们的偏振化方向成60°的夹角:
(1)如果两偏振片对光振动平行于其偏振化方向的光线均无吸收,则让自然光垂直入射后,其透射光强与入射光强之比是多少?
(2)如果两偏振片对光振动平行于其偏振化方向的光线分别吸收了10%的能量,则透射光强与入射光强之比为多少?
(1)自然光通过第一个偏振片后,光强为入射光强的一半,即

,透射光为线偏振光。由马吕斯定律,线偏振光通过第二个偏振片后,透射光强为
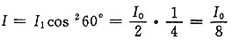
故

(2)光通过第一个偏振片后,透射光强为

光通过第一个偏振片,透射光强
I=I
1×cos
260°×(1-10%)
2 
故

四、分析计算题(要写出解题所依据的定理、定律、公式或相应的分析图。)
1. 一圆环形线圈a由50匝细线绕成,线圈截面积为4.0cm
2,放在另一个匝数为100匝,半径为20cm的圆环形线圈b的巾心,两线圈同轴,求:
(1)两线圈的互感;(真空中的磁导率μ
0=4π×10
-7T·m/A)
(2)当线圈a中的电流以50A/s的变化率减少时,线圈b内磁通量的变化率;
(3)线圈b的感生电动势。
(1)小线圈a的半径

可见小线圈a的半径远小于大线圈b的半径R,当大线圈b的电流为I
2时,小线圈a的面积上各点磁感应强度相同,其值为

所以I
2所激发的磁场B
2在线圈a中产生的磁链数为

则两线圈的互感为

(2)当小线圈a中电流为I
1时,它在大线圈b中产生的磁链数为
Ψ
21=N
2Φ
21=MI
1 因此线圈b内的磁通量变化率为
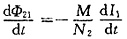

(3)大线圈b的感生电动势

 =Rcosπi+Rsinπj=-Ri
=Rcosπi+Rsinπj=-Ri =Rcos(2π)i+Rsin(2π)j=Ri
=Rcos(2π)i+Rsin(2π)j=Ri




 。
。
 mv2
mv2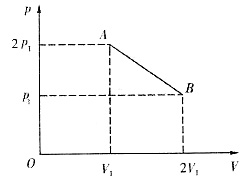
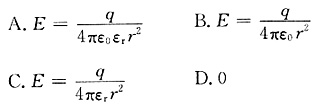
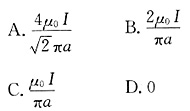

 。磁力fC>fA,因而aC<aA<aB。
。磁力fC>fA,因而aC<aA<aB。 B.
B.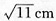
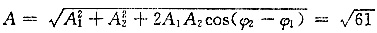 。
。
 。
。


 可得a、b两点间的相位差为
可得a、b两点间的相位差为 。
。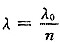 ,其中λ0为真空中的波长,n为介质的折射率;波速ν=νλ,ν不变,λ变小,所以波速也变小。
,其中λ0为真空中的波长,n为介质的折射率;波速ν=νλ,ν不变,λ变小,所以波速也变小。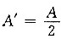 。
。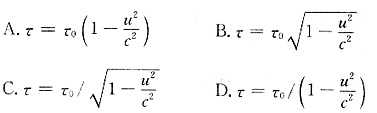
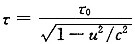 可得。
可得。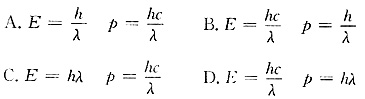
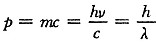 ,则能量
,则能量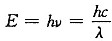 。
。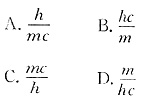
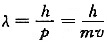 ,得
,得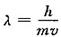 。
。 ,当车的速率减小到4km/h时,车走过的路程为______。
,当车的速率减小到4km/h时,车走过的路程为______。 则dr=vdt,
则dr=vdt,
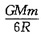
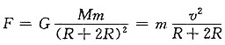

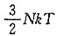

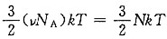 。
。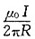
 ,在半圆内dl=rdθ,则
,在半圆内dl=rdθ,则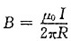 。
。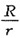




 (1)
(1) (2)
(2) 可得混合气体的压强为p=
可得混合气体的压强为p= (p1+p2)。
(p1+p2)。



 ,透射光为线偏振光。由马吕斯定律,线偏振光通过第二个偏振片后,透射光强为
,透射光为线偏振光。由马吕斯定律,线偏振光通过第二个偏振片后,透射光强为