一、选择题1. 函数f(x)在(a,b)内有反函数f
-1(x)存在,则f(x)必为
.
- A.有界函数
- B.严格单调上升
- C.严格单调下降
- D.以上结论都不正确
A B C D
D
[解析] 首先可知(A)不正确,例如

,x∈(0,1)无界,但它有反函数
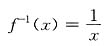
,x∈(1,+∞).其次,(B),(C)也不正确,试看反例:
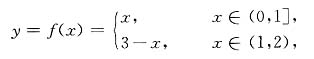
有反函数
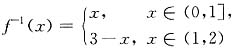
存在,但显然f(x)在(0,2)上无单调性.
3.
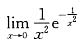
等于
.
(A)1 (B)
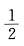
(C)0 (D)2
A B C D
C
[解析] 本题是“0·∞”型未定式的极限,可用洛必达法则.首先应将其化为“
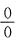
”型或“
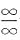
”型未定式,究竟化为哪一种,要视具体情况而定,如本题必须化为“
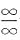
”型,即
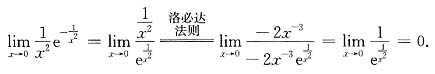
4.
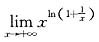
等于( ).
(A)∞ (B)0 (C)
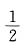
(D)1
A B C D
D
[解析] 这是“∞”型未定式,可用洛必达法则,但必须先化为“
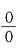
”型或“
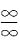
”型未定式,即
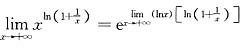
,而
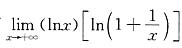
是“0·∞”型,若用洛必达法则去计算,则很难求出,这时必须用其他方法:
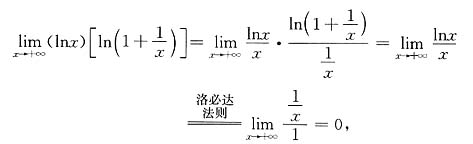
于是可知
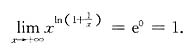
5.
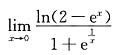
等于( ).
A B C D
B
[解析] 因为极限
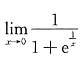
不存在,也不是未定式,所以无法用以上各种方法求此极限.
但是,由
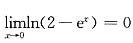
,且
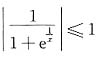
,可知,当x→0时,ln(2-e
x)为无穷小量,函数

是有界函数,因此它们之积仍为无穷小量,即
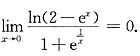
7.
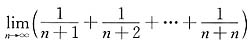
等于( ).
A B C D
D
[解析] 取函数
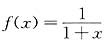
,x∈[0,1],将区间[0,1]n等分,分点为
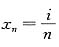
,i=0,1,…,n.在每个小区间[x
i-1,x
i]上取点ξ=x
i,i=1,2,…,n,则函数
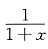
,x∈[0,1]的积分和为
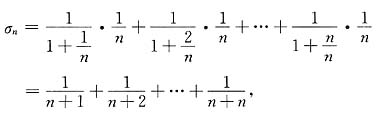
于是由定积分的定义
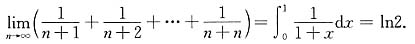
10. 下列数列中收敛的是( ).
(A){n
2} (B){e
-1/n}
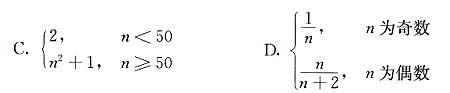
A B C D
B
[解析] (A)中,n→∞时,n
2→∞,发散;
(B)中,n→∞时,
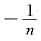
→0,e
-1/n→1,收敛;
(C)中,n→∞时,n
2+1→∞,发散;
(D)中,n→∞时,
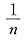
→0,
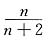
→1,其趋势不确定,发散.
11. 设
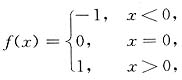
,则
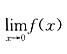
等于( ).
A B C D
C
[解析]
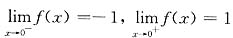
,故有
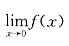
不存在.
所以应选(C).
13. 设函数f(x)在闭区间[a,b]上连续,且f(x)>0,则方程

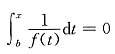
在区间(a,b)内的根是
.
A B C D
B
[解析] 令
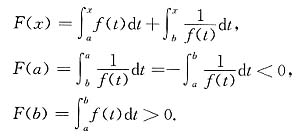
根据零点定理知,在(a,b)内至少存在一个根.
又因为
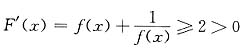
,即F(x)在[a,b]上单调增加.所以,F(x)=0在(a,b)内有且仅有一个根.
14.
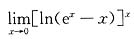
等于( ).
(A)0 (B)e (C)
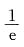
(D)1
A B C D
D
[解析] 这是“0
0”型未定式的极限,可用洛必达法则求之,即

而
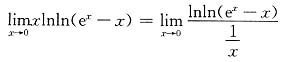

因此有
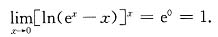
二、填空题1.
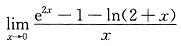
=______.
∞.
[解析] 因为
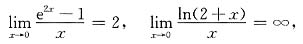
所以应填∞.
2. 设函数f(x)在x
0点可导,则
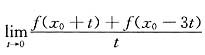
=______.
不能确定.
[解析] 因为
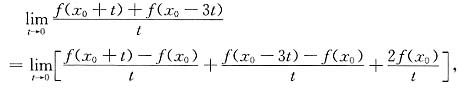
由于
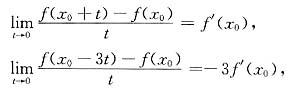
可知,当f(x
0)=0时,有
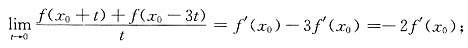
当f(x
0)≠0时,有
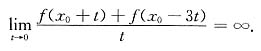
所以该极限值不存在.
3.
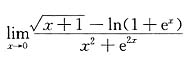
=______.
1-ln2.
[解析] 因为函数
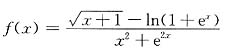
是初等函数,且在x=0点处有定义,可知f(x)在x=0点连续,即有
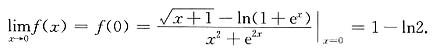
4. 设f'(1)=4,则

=______.
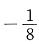
.
[解析] 因为

由f(x)在x=1点可导的定义,可知

,由此可得
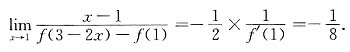
5.
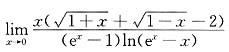
=______.
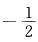
.
[解析] 这是“
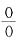
”型未定式的极限问题,可用洛必达法则求之.但我们先用等价无穷小将问题化简,然后再用洛必达法则,可使计算更为简洁.
原式
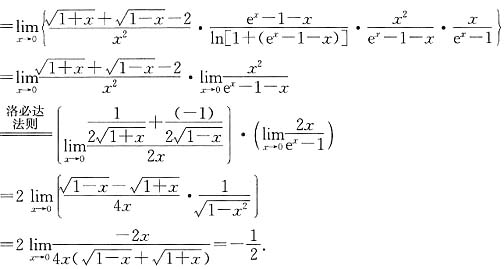
6. 已知
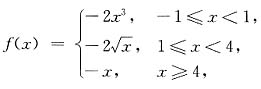
,则y=f
-1(x)的定义域为______.
(-∞,2].
[解析] 依题意,得
-1≤x<1时,f(x)=-2x
3,则-2<f(x)≤2;
1≤x<4时,f(x)=
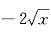
,则-4<f(x)≤-2;
x≥4时,f(x)=-x,则f(x)≤-4.
即f(x)的值域为(-∞,2].
又因为y=f
-1(x)的定义域即为y=f(x)的值域,故f
-1(x)的定义域为(-∞,2].
7. 设函数f(x)在(-∞,+∞)上满足2f(1+x)+f(1-x)=3e
x,则f(x)=______.
2ex-1-e1-x.
[解析] 用-x代入等式,有
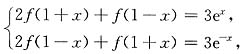
由此可解得f(1+x)=2e
x-e
-x,令1+x=t,有
f(t)=2e
t-1-e
1-t,
即知f(x)=2e
x-1-e
1-x.
8. 设函数
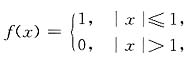
则函数f[f(x)]=______.
1.
[解析] 因为由已知条件知
|f(x)|≤1,-∞<x<+∞,
所以由f(x)及复合函数的定义知
f[f(x)]=1,-∞<x<+∞.
9.
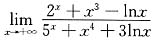
=______.
[解析] 利用在加减法中,较低阶的无穷大量与较高阶的无穷大量相比较可以忽略的性质求解.
因为x→+∞时,分子2
x+x
3-lnx是无穷大量,且为几个无穷大量的和、差,并且2
x>>x
3>>lnx,所以lnx,x
3与2
x相比都可以忽略.同理,分母中的3lnx,x
4与5
x相比也可以忽略,因此原极限可以视为

,故
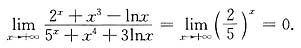
10.
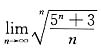
=______.
5.
[解析] 本题使用夹逼准则.
由于

而
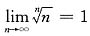
,且

.故由夹逼准则知
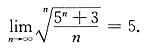
11. 若
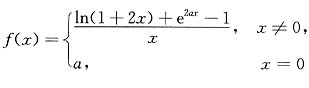
在(-∞,+∞)上连续,则a=______.
-2.
[解析] 若f(x)在(-∞,+∞)上连续,则f(x)必在x=0处连续.即

而

所以2+2a=a,则a=-2.
12. 设函数
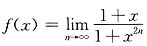
,则函数f(x)的间断点为______.
x=1.
[解析] 当|x|<1时,
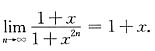
当|x|>1时,
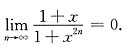
故
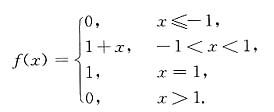
由于
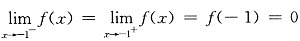
,所以x=-1为连续点;而
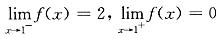
,所以x=1为间断点.
13.
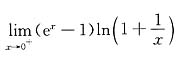
=______.
0.
[解析] 这是“0·∞”型的未定式的极限,若立即化为“
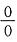
”型或“
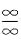
”型未定式,用洛必达法则很难计算,应先用等价无穷小,再用洛必达法则,即
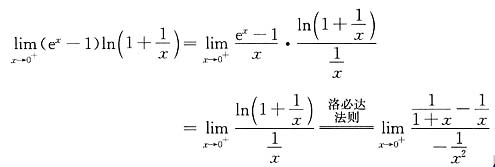
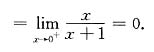
14.

=______.
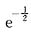
.
[解析] 这是数列的极限,应通过函数的极限来计算,即考虑极限
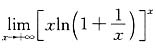
,这是“1
∞”型未定式,可用洛必达法则求之:
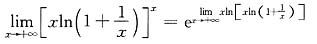
而

于是有
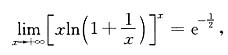
即
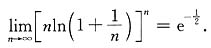
15.
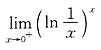
=______.
1.
[解析] 这是“∞
0”型未定式的极限,可用洛必达法则计算,即
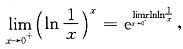
而
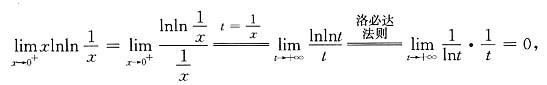
由此可得
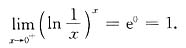
三、计算题1. 设函数f(x)定义在(-∞,+∞),试判别函数g(x)=f(x)+f(-x)与h(x)=f(x)-f(-x)的奇偶性.
[解] 对于(-∞,+∞)上的任一点x,有g(-x)=f(-x)+f[-(-x)]=f(x)+f(-x)=g(x),所以函数g(x)为偶函数.又因h(-x)=f(-x)-f[-(-x)]=f(-x)-f(x)=-h(x),所以函数h(x)为奇函数.
2. 已知函数f(x)满足f(x
3)+2f(
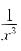
)-3x,x≠0,试求f(x).
[解] 作换元t=x
3,则有
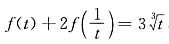
,t≠0,可知
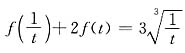
,t≠0.由以上两式,解方程可得
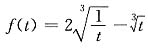
,t≠0,即有
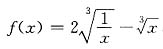
,x≠0.
3. 判别下列函数的奇偶性:
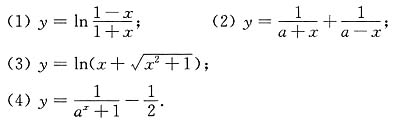
[解] (1)对于(-1,1)内任一点x,有
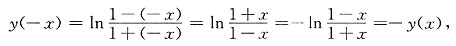
所以为奇函数.
(2)对于任意不等于±a的x点,有
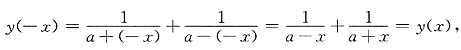
所以为偶函数.
(3)对于(-∞,+∞)内任一点x,有
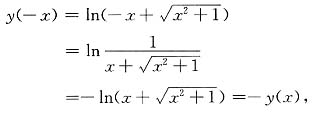
所以为奇函数.
(4)对于(-∞,+∞)内的任一点x,有
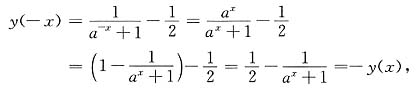
所以为奇函数.
4. 求
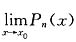
.
[解] 原式
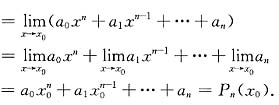
5. 分别求出在x趋于1,0和∞时,函数
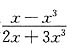
的极限值.
[解]
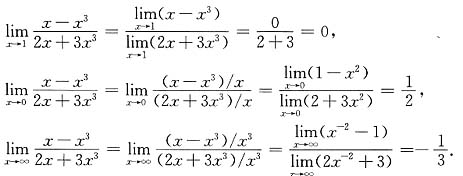
8. 求
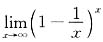
.
[解]
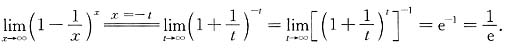
9. 求
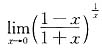
.
[解]
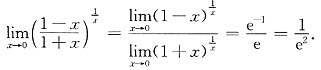
10. 若函数f(x)在x=1点处连续,且极限
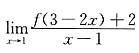
存在,试求f(1).
[解] 因为f(x)在x=1点处连续,所以有
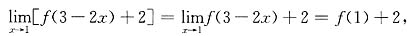
又由极限运算法则有
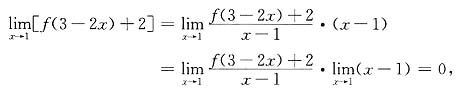
由此可知有f(1)+2=0,即得f(1)=-2.
11. 证明方程x
5-3x-1=0在(1,2)内至少有一个实根.
[证] 考虑函数f(x)=x5-3x-1,作为初等函数,可知其在[1,2]上连续,且f(1)=-3<0,f(2)=25>0,于是可知该方程在(1,2)内至少有一个实根.
12. 求极限
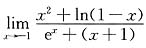
.
[解] 因为初等函数
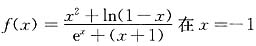
点处有定义,所以在该点连续,即有
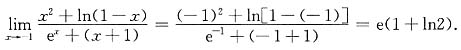
13. 求极限
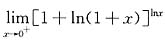
.
[解] 先应将函数化为可用幂指函数求极限的形式,即
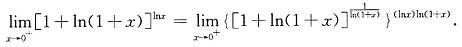
于是,由
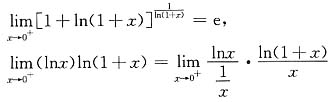

可得
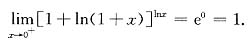
14. 求极限
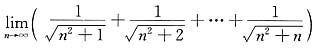
.
15. 求极限
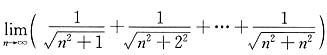
.
[解] 可利用定积分定义域求此极限.
取函数
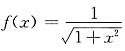
,x∈[0,1].将区间[0,1]n等分,分点为

,i=0,1,2,…,n.在每个小区间[x
i-1,x
i]中取一点
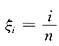
,i=1,2,…,n.由定积分定义可知有
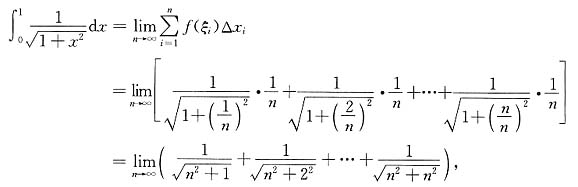
而定积分
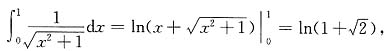
结果有
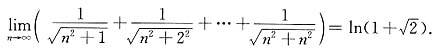
16. 求极限
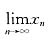
,其中
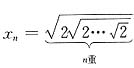
.
[解] 显然有x
n≤x
n+1,即数列{x
n}单调上升.
又若将x
n中最后一个2放大成4,则有
x
n≤2,n=1,2,…,可见数列{x
n}有上界.因此按极限存在准则知
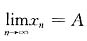
存在,下面来求A因为
x
n+12=2x
n,n=1,2,…,当n→∞时,有A
2=2A,可得A=0或A=2,显然A=0不合题意,因为
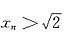
,n=1,2,…,所以
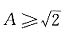
,于是
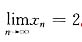
.
17. 试求函数
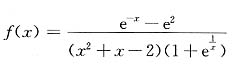
的连续区间、间断点及其类型.
[解] 因为f(x)是初等函数,其定义域为
(-∞,-2)∪(-2,0)∪(0,1)∪(1,+∞),即是f(x)的连续区间,间断点为x
1=-2,x
2=0,x
3=1.下面来确定间断点的类型.
当x
1=-2时,由
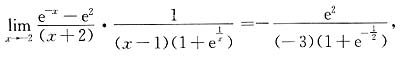
可见x
1=-2是f(x)的可去间断点.
当x
2=0时,由于
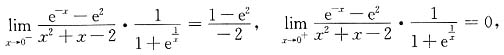
可见x
2=0是跳跃间断点.
当x
3=1时,由于
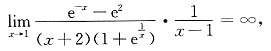
可知x
3=1是f(x)的第二类间断点.
18.
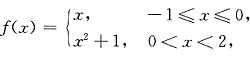
求其定义域.
[解] 这是一个分段函数,其定义域为[-1,2).
19.
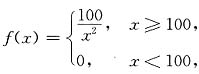
,求其定义域.
20. 下列函数是由哪些简单函数复合而成的?
(1)
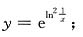
(2)
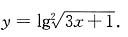
[解] (1)由y=e
u,u=v
2,v=lnt,
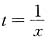
复合而成,其中u,v,t为中间变量.
(2)由y=u
2,u=lgv,
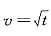
,t=3x+1复合而成,其中u,v,t为中间变量.
21. 求下列函数的反函数及其定义域.
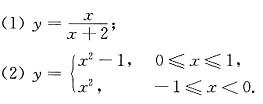
[解] (1)由表达式
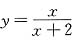
解出
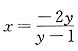
,再将x与y位置互换,得反函数
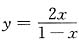
.其定义域为x≠1的所有实数,即为(-∞,1)∪(1,+∞).
(2)对于分段函数要分段解出反函数表达式,当0≤x≤1时,解出

,此时-1≤y≤0,当-1≤x<0时,解出
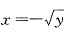
,此时0<y≤1,将x与y互换位置,写出反函数的分段表示式为
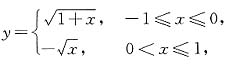
定义域为[-1,1].
 ,x∈(0,1)无界,但它有反函数
,x∈(0,1)无界,但它有反函数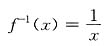 ,x∈(1,+∞).其次,(B),(C)也不正确,试看反例:
,x∈(1,+∞).其次,(B),(C)也不正确,试看反例: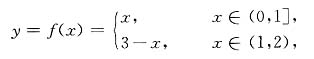 有反函数
有反函数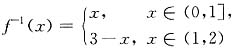 存在,但显然f(x)在(0,2)上无单调性.
存在,但显然f(x)在(0,2)上无单调性.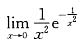 等于 .
等于 .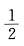 (C)0 (D)2
(C)0 (D)2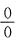 ”型或“
”型或“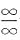 ”型未定式,究竟化为哪一种,要视具体情况而定,如本题必须化为“
”型未定式,究竟化为哪一种,要视具体情况而定,如本题必须化为“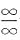 ”型,即
”型,即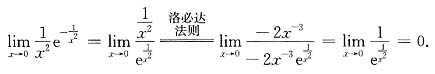
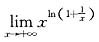 等于( ).
等于( ).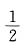 (D)1
(D)1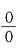 ”型或“
”型或“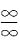 ”型未定式,即
”型未定式,即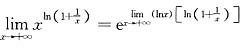 ,而
,而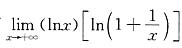 是“0·∞”型,若用洛必达法则去计算,则很难求出,这时必须用其他方法:
是“0·∞”型,若用洛必达法则去计算,则很难求出,这时必须用其他方法: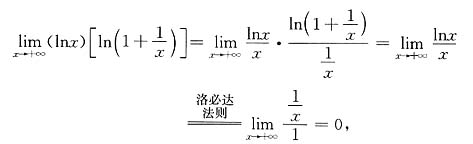 于是可知
于是可知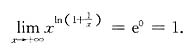
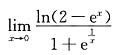 等于( ).
等于( ).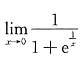 不存在,也不是未定式,所以无法用以上各种方法求此极限.
不存在,也不是未定式,所以无法用以上各种方法求此极限.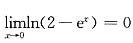 ,且
,且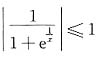 ,可知,当x→0时,ln(2-ex)为无穷小量,函数
,可知,当x→0时,ln(2-ex)为无穷小量,函数 是有界函数,因此它们之积仍为无穷小量,即
是有界函数,因此它们之积仍为无穷小量,即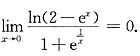
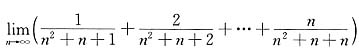 等于( ).
等于( ).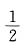 (B)1 (C)
(B)1 (C)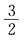 (D)2
(D)2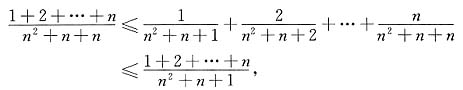 而
而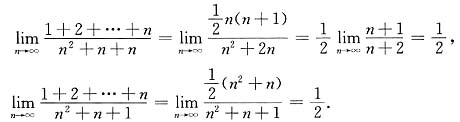 由夹逼定理即知
由夹逼定理即知
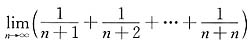 等于( ).
等于( ).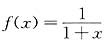 ,x∈[0,1],将区间[0,1]n等分,分点为
,x∈[0,1],将区间[0,1]n等分,分点为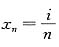 ,i=0,1,…,n.在每个小区间[xi-1,xi]上取点ξ=xi,i=1,2,…,n,则函数
,i=0,1,…,n.在每个小区间[xi-1,xi]上取点ξ=xi,i=1,2,…,n,则函数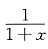 ,x∈[0,1]的积分和为
,x∈[0,1]的积分和为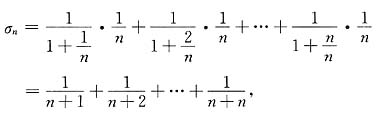
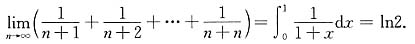

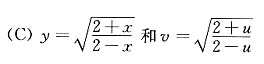
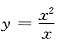
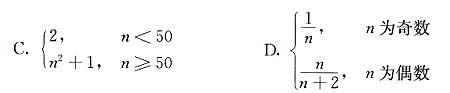
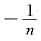 →0,e-1/n→1,收敛;
→0,e-1/n→1,收敛;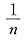 →0,
→0,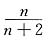 →1,其趋势不确定,发散.
→1,其趋势不确定,发散.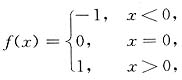 ,则
,则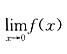 等于( ).
等于( ).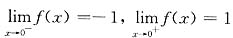 ,故有
,故有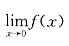 不存在.
不存在.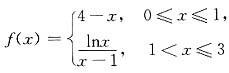 ,在x=1点间断是因为( ).
,在x=1点间断是因为( ).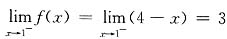 ,f(x)的右极限为
,f(x)的右极限为 ,因此f(x)的左、右极限都存在,但不相等,从而f(x)在x=1点间断.
,因此f(x)的左、右极限都存在,但不相等,从而f(x)在x=1点间断.
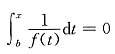 在区间(a,b)内的根是 .
在区间(a,b)内的根是 .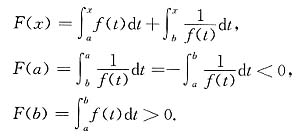
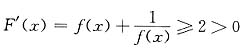 ,即F(x)在[a,b]上单调增加.所以,F(x)=0在(a,b)内有且仅有一个根.
,即F(x)在[a,b]上单调增加.所以,F(x)=0在(a,b)内有且仅有一个根.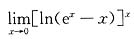 等于( ).
等于( ).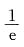 (D)1
(D)1 而
而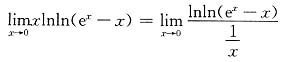

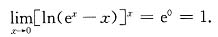
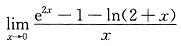 =______.
=______.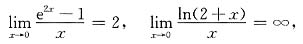 所以应填∞.
所以应填∞.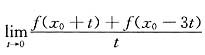 =______.
=______.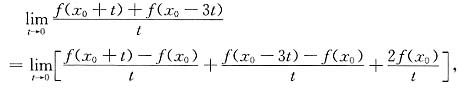 由于
由于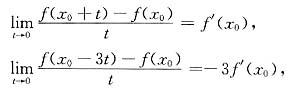 可知,当f(x0)=0时,有
可知,当f(x0)=0时,有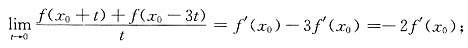 当f(x0)≠0时,有
当f(x0)≠0时,有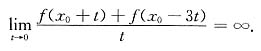 所以该极限值不存在.
所以该极限值不存在.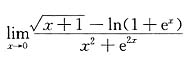 =______.
=______.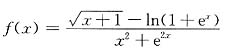 是初等函数,且在x=0点处有定义,可知f(x)在x=0点连续,即有
是初等函数,且在x=0点处有定义,可知f(x)在x=0点连续,即有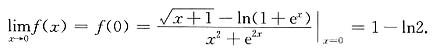
 =______.
=______.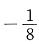 .
.
 ,由此可得
,由此可得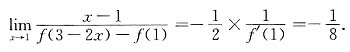
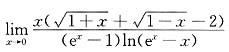 =______.
=______.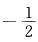 .
.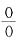 ”型未定式的极限问题,可用洛必达法则求之.但我们先用等价无穷小将问题化简,然后再用洛必达法则,可使计算更为简洁.
”型未定式的极限问题,可用洛必达法则求之.但我们先用等价无穷小将问题化简,然后再用洛必达法则,可使计算更为简洁.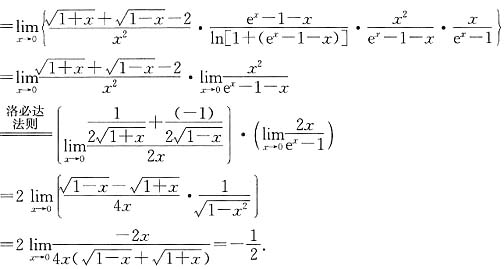
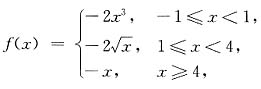 ,则y=f-1(x)的定义域为______.
,则y=f-1(x)的定义域为______.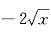 ,则-4<f(x)≤-2;
,则-4<f(x)≤-2;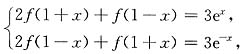
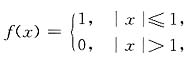 则函数f[f(x)]=______.
则函数f[f(x)]=______.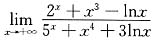 =______.
=______. ,故
,故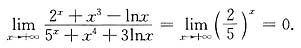
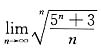 =______.
=______.
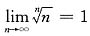 ,且
,且 .故由夹逼准则知
.故由夹逼准则知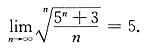
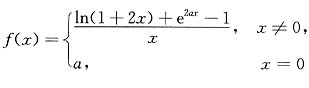 在(-∞,+∞)上连续,则a=______.
在(-∞,+∞)上连续,则a=______. 而
而 所以2+2a=a,则a=-2.
所以2+2a=a,则a=-2.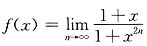 ,则函数f(x)的间断点为______.
,则函数f(x)的间断点为______.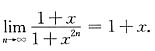
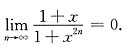
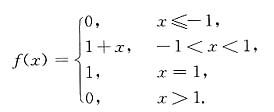
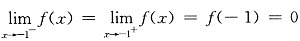 ,所以x=-1为连续点;而
,所以x=-1为连续点;而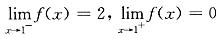 ,所以x=1为间断点.
,所以x=1为间断点.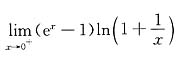 =______.
=______.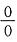 ”型或“
”型或“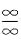 ”型未定式,用洛必达法则很难计算,应先用等价无穷小,再用洛必达法则,即
”型未定式,用洛必达法则很难计算,应先用等价无穷小,再用洛必达法则,即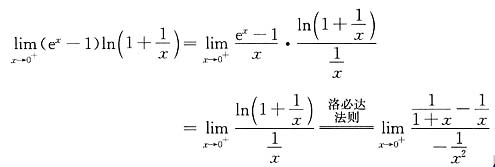
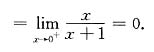
 =______.
=______.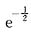 .
.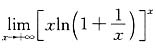 ,这是“1∞”型未定式,可用洛必达法则求之:
,这是“1∞”型未定式,可用洛必达法则求之: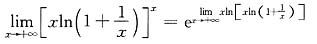 而
而 于是有
于是有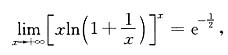 即
即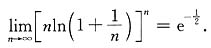
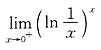 =______.
=______.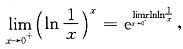
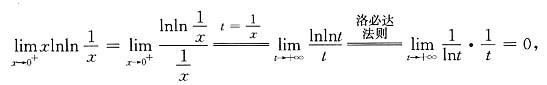 由此可得
由此可得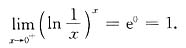
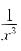 )-3x,x≠0,试求f(x).
)-3x,x≠0,试求f(x).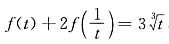 ,t≠0,可知
,t≠0,可知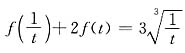 ,t≠0.由以上两式,解方程可得
,t≠0.由以上两式,解方程可得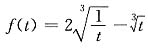 ,t≠0,即有
,t≠0,即有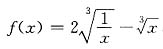 ,x≠0.
,x≠0.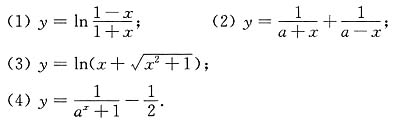
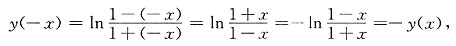 所以为奇函数.
所以为奇函数.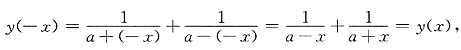 所以为偶函数.
所以为偶函数.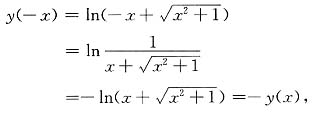 所以为奇函数.
所以为奇函数.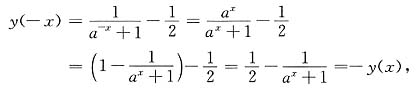 所以为奇函数.
所以为奇函数.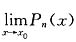 .
.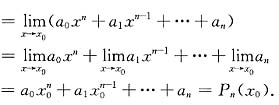
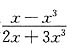 的极限值.
的极限值.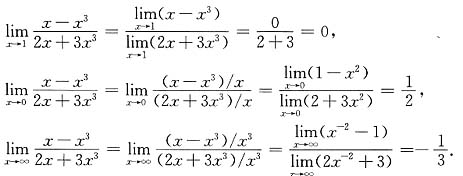
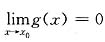 ,且
,且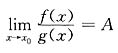 存在,证明:
存在,证明: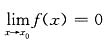 .
.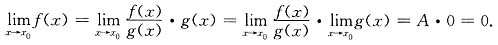
 ,求
,求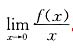 .
. 即有
即有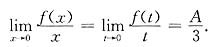
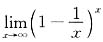 .
.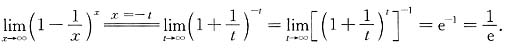
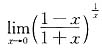 .
.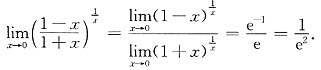
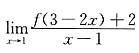 存在,试求f(1).
存在,试求f(1).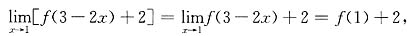 又由极限运算法则有
又由极限运算法则有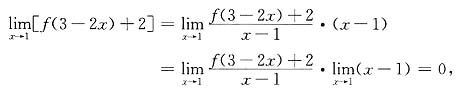
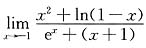 .
.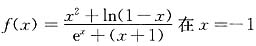 点处有定义,所以在该点连续,即有
点处有定义,所以在该点连续,即有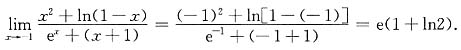
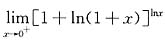 .
.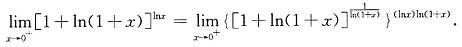 于是,由
于是,由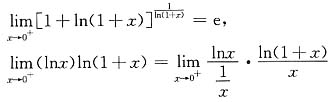

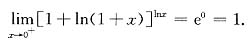
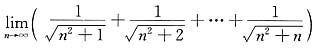 .
. 且有
且有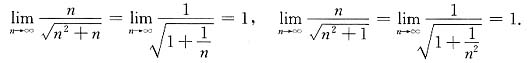 由夹逼定理可知
由夹逼定理可知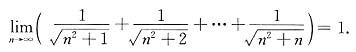
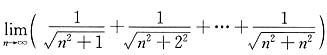 .
.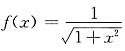 ,x∈[0,1].将区间[0,1]n等分,分点为
,x∈[0,1].将区间[0,1]n等分,分点为 ,i=0,1,2,…,n.在每个小区间[xi-1,xi]中取一点
,i=0,1,2,…,n.在每个小区间[xi-1,xi]中取一点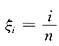 ,i=1,2,…,n.由定积分定义可知有
,i=1,2,…,n.由定积分定义可知有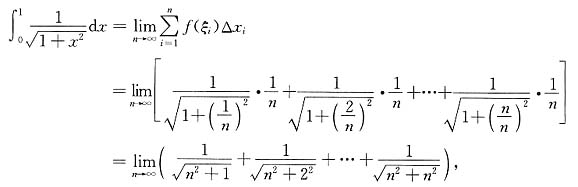
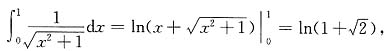
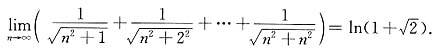
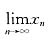 ,其中
,其中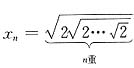 .
.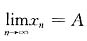 存在,下面来求A因为
存在,下面来求A因为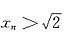 ,n=1,2,…,所以
,n=1,2,…,所以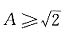 ,于是
,于是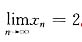 .
.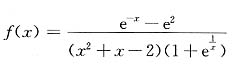 的连续区间、间断点及其类型.
的连续区间、间断点及其类型.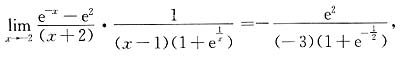 可见x1=-2是f(x)的可去间断点.
可见x1=-2是f(x)的可去间断点.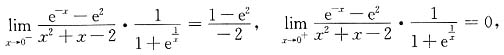 可见x2=0是跳跃间断点.
可见x2=0是跳跃间断点.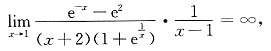
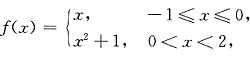 求其定义域.
求其定义域.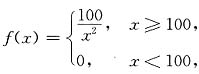 ,求其定义域.
,求其定义域.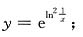
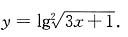
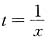 复合而成,其中u,v,t为中间变量.
复合而成,其中u,v,t为中间变量.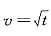 ,t=3x+1复合而成,其中u,v,t为中间变量.
,t=3x+1复合而成,其中u,v,t为中间变量.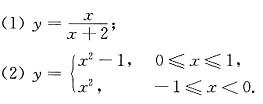
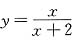 解出
解出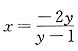 ,再将x与y位置互换,得反函数
,再将x与y位置互换,得反函数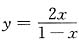 .其定义域为x≠1的所有实数,即为(-∞,1)∪(1,+∞).
.其定义域为x≠1的所有实数,即为(-∞,1)∪(1,+∞). ,此时-1≤y≤0,当-1≤x<0时,解出
,此时-1≤y≤0,当-1≤x<0时,解出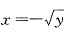 ,此时0<y≤1,将x与y互换位置,写出反函数的分段表示式为
,此时0<y≤1,将x与y互换位置,写出反函数的分段表示式为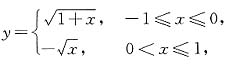 定义域为[-1,1].
定义域为[-1,1].