一、数字推理给你一个数列,但其中缺少一项,要求你仔细观察数列的排列规律。然后从四个供选择的选项中选出你认为最合理的一项。
二、数学运算在这部分试题中,每道试题呈现一段表述数字关系的文字,要求你迅速、准确地计算出答案。
3. 甲、乙两厂生产同一种玩具,甲厂生产的玩具数量每个月保持不变,乙厂生产的玩具数量每个月增加一倍。已知今年1月份甲、乙两厂生产的玩具的总数是98件,2月份甲、乙两厂生产的玩具的总数是106件,那么乙厂今年生产的玩具数量总和第一次超过甲厂生产的玩具数量总和是在
月份。
A B C D
A
[解析] 由题意可知,2月份甲生产玩具数量不变,乙生产的比上月多1倍,且1月甲、乙共生产98件,2月共生产106件,所以乙多生产106-98=8件。即乙第一个月生产8件,每个月生产件数是以8为首项,公比为2的等比数列。设生产了n个月,则甲共生产90n件,根据等比数列求和公式乙生产了
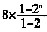
=8×(2
n-1)=2
n+3-8件。结合选项,从最小的选项代入验证,当n=7时,2
n+3-8=1016,90n=630。因此,7月份时乙生产的玩具总量就超过甲了,选A。
4. 某人共收集邮票若干张,其中
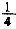
是2007年以前的国内发行的邮票,
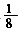
是2008年国内发行的,
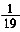
是2009年国内发行的,此外尚有不足100张的国外邮票。则该人共有
张邮票。
A B C D
C
[解析] 剩下的国外邮票占总邮票数的
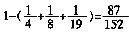
。代入选项,当邮票总数为152张时,国外邮票才是整数,为87张,符合题意。
另解,由题意可知,邮票数应该是8和19的倍数,选项中只有C项满足。
第二部分 言语理解与表达本部分包括表达与理解两方面的内容。请根据题目要求,在四个选项中选出一个最恰当的答案。
23. 依次填入下面一段文字横线处的语句,衔接最恰当的一组是
。
“开卷有益”是说打开书就一定会有收获。______。______,______,______,______。______,如果你勤读书、读好书,你就一定能真正体会到读书的乐趣。
①使人们不断完善,走向进步
②当然,有的书是有缺点的,要善于选择
③确实,书是人类最好的朋友、最好的老师
④书是人类获得知识的重要途径
⑤歌德曾说过“读一本好书就是和许多高尚的人谈话”
⑥读书能帮助人们看清世间的美与丑
- A.②⑥⑤④①③
- B.③⑥②⑤①④
- C.④③①⑥②⑤
- D.⑤③④⑥①②
A B C D
D
[解析] 除②句外,其他五句说的都是读书的好处,基于话题一致的考虑,其他五句应相连,排除B、C。②句说的是“要善于选择”,这与后文的“读好书”相对应,故②应排最后。本题选D。
“今天,你节省了多少碳?”有一群“环保达人”,自觉地少开私家车、坚持走楼梯,电脑不用就关机,用清单列出自己一天的碳排放总量,并把“减碳日记”实时挂到网上……这就是眼下正时兴的“低碳生活”。进入2011年,低碳与生活的联系更加紧密。
人们在生活和消费过程中的过量碳排放,是造成全球气候变暖的因素之一。针对这一点,低碳生活要求人们在日常生活中养成节能的好习惯,减少碳排放,建设资源节约型、环境友好型社会,促进入与自然和谐发展,提升生活质量。
作为可持续的绿色生活方式,低碳生活将是协调经济社会发展和环境保护的重要途径。而从长远看,这更是一种着眼于未来的生活理念。低碳生活受到“低碳族”的响应,与其本身所蕴涵的环保元素和道德魅力密不可分。
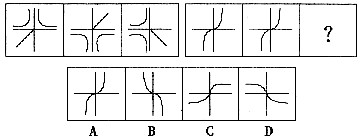
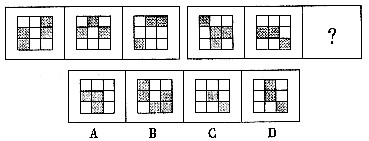
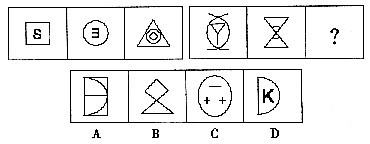
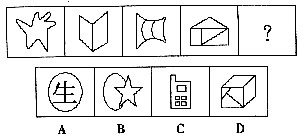
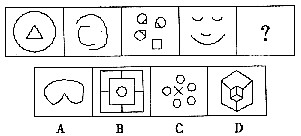
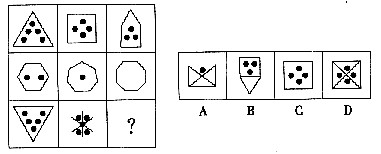
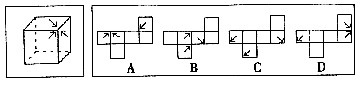
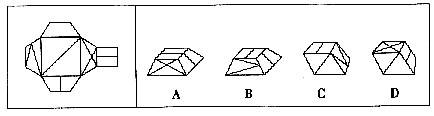
低碳生活是健康绿色的生活习惯,是更加时尚的消费观,是全新的生活质量观。“雁过留声,人过不留碳”。低碳生活不是口号而是理念,把握机遇,才能掌握将来发展,选择低碳生活,才能享受美好未来。 一、图形推理每道题在左边的题干中给出一套图形,其中包括五个图,这五个图形呈现一定的规律性。在右边给出了四个图。请从中选出一个作为保持左边五个图规律性的第六个图。
二、逻辑判断每题给出一段陈述,这段陈述被假设是正确的,不容置疑的。要求你根据这段陈述,选择一个答案。注意,正确的答案应与所给出的陈述相符合。不需要任何附加说明即可以从陈述中直接推出。
4. 短跑决赛中,前三名甲、乙、丙是A、B、C队的选手。已知:
①A队选手的成绩比B队选手的成绩好
②C队选手的成绩比乙差
⑧C队选手的成绩比丙好
根据上述条件,下列选项中,肯定为真的是
。
- A.甲、乙、丙依次为C队、B队和A队选手
- B.C队选手是冠军,A队选手是亚军,B队选手是季军
- C.甲、乙、丙依次为C队、A队和B队选手
- D.A队选手是冠军,B队选手是亚军,C队选手是季军
A B C D
C
[解析] 分析推理类题目。运用排序法,①可以转化为:A>B;②③可以转化为:丙<C<乙,可推出丙<乙;因此乙是A队选手,丙是B队选手;进而得出,甲是C队选手且B<C<A。对比选项,C项正确。故答案选C。
9. 某大学进行论文比赛,得第一名的只能有一人。究竟谁得第一名?在对甲、乙、丙、丁、戊、己六个参赛者进行名次预测时,四人作了如下的预测:
甲:取得第一名的要么是我,要么是乙。
乙:取得第一名的要么是甲.要么是丙。
丙:如果不是戊取得第一名,就一定是己。
丁:第一名绝不会是甲。
比赛结束后,发现只有一个人的预测是正确的。请问:谁得第一名?
A B C D
D
[解析] 分析推理题。方法一:此题甲、乙和丁的预测都涉及了甲,因此可以将丁的预测作为突破口。假设丁预测错误,得第一名的是甲,则甲、乙的预测都正确,不符合只有一个人的预测正确:所以丁的预测正确,得第一名的不是甲,则甲、乙、丙的预测都错误。由甲和乙预测错误可知,取得第一名的不是甲、乙、丙;由丙的预测错误可知,取得第一名的不是戊和己,故取得第一名的只能是丁。
方法二:此题也可用代入法。将A项代入,甲得第一名,则甲和乙的预测都正确,不符合题意;将B项代入,甲和丁的预测都正确,不符合题意;将C项代入,乙和丁的预测都正确,不符合题意。故答案选D。
三、定义判断每道题先给出一个概念的定义,然后分别列出四种情况,要求你严格依据定义。从中选择一个最符合或最不符合该定义的答案。注意:假设这个定义是正确的,不容置疑的。
四、类比推理题干中给出具有某种关系的两个词(词组),请从四个备选项中选出一组,其间的关系与题干所给出的两个词(词组)间的关系最为贴近或最为相似。
五、事件排序每道题给出5个事件,每个事件是以简短语句表述的,接着给出表示事件的四种假定发生顺序的四个数字排列。请你选出其中最合乎逻辑的一种事件排序。
第四部分 常识判断根据题目要求,在四个选项中,选出一个正确答案。
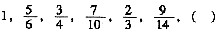

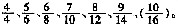



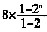 =8×(2n-1)=2n+3-8件。结合选项,从最小的选项代入验证,当n=7时,2n+3-8=1016,90n=630。因此,7月份时乙生产的玩具总量就超过甲了,选A。
=8×(2n-1)=2n+3-8件。结合选项,从最小的选项代入验证,当n=7时,2n+3-8=1016,90n=630。因此,7月份时乙生产的玩具总量就超过甲了,选A。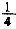 是2007年以前的国内发行的邮票,
是2007年以前的国内发行的邮票,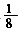 是2008年国内发行的,
是2008年国内发行的,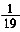 是2009年国内发行的,此外尚有不足100张的国外邮票。则该人共有 张邮票。
是2009年国内发行的,此外尚有不足100张的国外邮票。则该人共有 张邮票。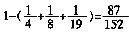 。代入选项,当邮票总数为152张时,国外邮票才是整数,为87张,符合题意。
。代入选项,当邮票总数为152张时,国外邮票才是整数,为87张,符合题意。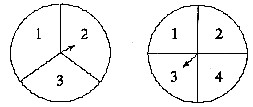

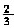 ,第二个转盘指到奇数的概率为
,第二个转盘指到奇数的概率为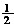 ,则总的概率为
,则总的概率为 。
。


 ;2009年上半年与2008年同期相比,比重提高了12.6÷29.7×100-
;2009年上半年与2008年同期相比,比重提高了12.6÷29.7×100-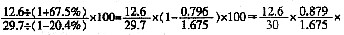 100≈42×0.5=21个百分点,最接近的就是C。
100≈42×0.5=21个百分点,最接近的就是C。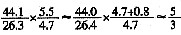 ×1.2=2万元/平方米,最接近的就是B。
×1.2=2万元/平方米,最接近的就是B。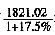 >1800÷1.2=1500亿元,选D。
>1800÷1.2=1500亿元,选D。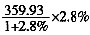 )亿元,重工业产值增长量(
)亿元,重工业产值增长量(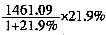 )亿元。则所求为
)亿元。则所求为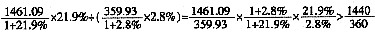 ×
×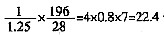 =4×0.8×7=22.4,并且
=4×0.8×7=22.4,并且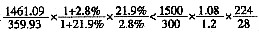 =5×0.9×8=36.0倍。选C。
=5×0.9×8=36.0倍。选C。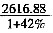 亿元,则上海市六个重点发展工业行业平均每个行业完成工业产值为
亿元,则上海市六个重点发展工业行业平均每个行业完成工业产值为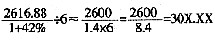 亿元。
亿元。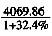 亿元,2009年2月份规模以上工业总产值为
亿元,2009年2月份规模以上工业总产值为 亿元,则2009年1月规模以上工业总产值为
亿元,则2009年1月规模以上工业总产值为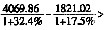
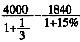 =3000-1840×
=3000-1840×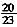 =3000-1600=1400亿元,A正确;B项,由文字部分可知,B正确;C项,观察表格第三列可知,2月份同比增长超过30%的行业分别是电子信息产品制造业、汽车制造业、精品钢材制造业,只有3个,C错误;D项,由第111题可知,2009年2月份全市工业总产值为1549.8亿元,轻工业完成产值为
=3000-1600=1400亿元,A正确;B项,由文字部分可知,B正确;C项,观察表格第三列可知,2月份同比增长超过30%的行业分别是电子信息产品制造业、汽车制造业、精品钢材制造业,只有3个,C错误;D项,由第111题可知,2009年2月份全市工业总产值为1549.8亿元,轻工业完成产值为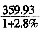 亿元,则2009年2月轻工业完成产值占全市工业总产值的比重约为
亿元,则2009年2月轻工业完成产值占全市工业总产值的比重约为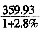 ÷1549.8=22.6%,D正确。
÷1549.8=22.6%,D正确。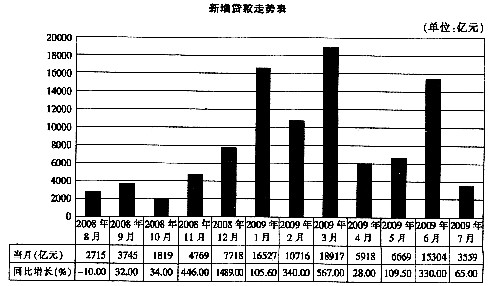
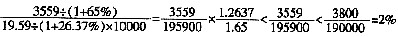 ,则所求一定小于2%×100=2个百分点,排除D、选择B。
,则所求一定小于2%×100=2个百分点,排除D、选择B。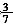 ≈43%。应选择D。
≈43%。应选择D。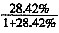 ;M1增速为26.37%,增量为19.59÷(1+26.37%)×26.37%=19.59×
;M1增速为26.37%,增量为19.59÷(1+26.37%)×26.37%=19.59×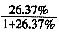 ,明显57.30>19.59,28.42%>26.37%,则M2同比增速、增量均大于M1,Ⅲ正确。
,明显57.30>19.59,28.42%>26.37%,则M2同比增速、增量均大于M1,Ⅲ正确。
 深色:已答题 浅色:未答题
深色:已答题 浅色:未答题
