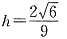一、填空题1. 班级管理的主要模式有:______、平等管理、______和目标管理.
2. 主张“有教无类”的古代教育家是______.
3. 被称为“危险期”或“心理断乳期”的时期发生在______阶段.
4. 古希腊提出问答法的哲学家和思想家是______.
5. 班主任是班级建设的设计者,是班组组织的领导者,又是班组人际关系的______.
6. 发展个性是教育的理想,进行个性教育是教育的______和真谛.
7. 素质教育是以培养______和______为重点的教育.
8. 教学过程中领会知识,包括使学生______教材和______教材.
9. 师生关系在人格上是______的关系,在社会道德上是______的关系.
10. 根据课程标准编制的、系统反映学科内容的教学用书称为______.
二、简答题1. 学校教育在影响人的发展上具有哪些独特的功能?
(1)学校教育按社会对个体的基本要求对个体发展的方向与方面作出社会性规范.
(2)学校教育具有加速个体发展的特殊功能.
(3)学校教育,尤其是基础教育对个体发展的影响不仅具有即时的价值,而且具有延时的价值.
(4)学校教育具有开发个体特殊才能和发展个性的功能.
2. 教学的主要作用有哪些?
(1)教学是社会经验得以再生产的一种主要手段.
(2)教学为个人全面发展提供科学的基础和实践.
(3)教学是教育工作构成的主体部分,又是教育的基本途径.
3. 试述我国中学德育的基本原则,
(1)导向性原则.
(2)疏导原则.
(3)尊重学生与严格要求学生相结合原则.
(4)教育的一致性与连贯性原则.
(5)因材施教原则,
三、论述题1. 你认为中学数学教师的语言技能主要包含哪些方面的内容.
中学数学教师的语言技能有着教学语言的共性和数学语言自身的特征,主要体现在以下几个方面:
(1)教师的数学教学语言必须具有科学性;
(2)教师的数学教学语言必须体现教育性;
(3)教师的数学教学语言必须具有启发性、趣味性;
(4)教师的数学教学语言必须符合学生的特点;
(5)教师必须掌握多种口语技巧,并能在教学过程中灵活运用;
(6)教师必须具有合理使用身体语言的技能.
一、单项选择题3. 在等差数列{a
n}中,a
1=-2008,其前n项和为S
n,若
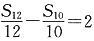
,则S
2008的值等于______.
- A.-2007
- B.-2008
- C.2007
- D.2008
A B C D
B
[解析] 因为

,所以d=2,S
2008=
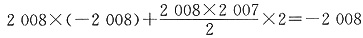
. 答案为-2008. 故选B.
6. 设a、b、c是空间三条直线,α、β是空间两个平面,则下列命题中,逆命题不成立的是______.
A.当c⊥α时,若c⊥β,则α//β
B.当
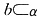
时,若b⊥β,则a⊥β
C.当
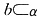
时,且c是a在α内的射影时,若b⊥c,则α⊥b
D.当
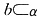
时,且
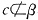
,若c∥α,则b∥c
A B C D
B
[解析] 当α⊥β时,平面α内的直线不一定垂直于平面β.故选B.
9. 已知等差数列{a
n}前17项和S
17=51,则a
5-a
7+a
9-a
11+a
13=______.
A B C D
A
[解析] S17=a1+…+a17=(2a1+16d)×8+(a1+8d)=(a1+8d)×17=51,a1+8d=3,即a9=3.数列为等差数列,则:a5-a7+a9-a11+a13=a9+(a5+a13)-(a7+a11)=a9=3.故选A.
二、填空题1. 已知实数x,y满足
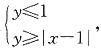
则x+2y的最大值是______.
2. 设直线ax-y+3=0与圆(x-1)
2+(y-2)
2=4相交于A、B两点,且弦AB的长为
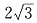
,则a=______.
3. 表面积为4π的球O与平面角为钝角的二面角的两个半平面相切于A、B两点,三角形OAB的面积
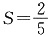
,则球心到二面角的棱的距离为______.
4. 甲、乙、丙、丁4个人站成一横排,若甲必须站在乙左边,则共有站法(用数字作答)______种.
5. 若x<3,则
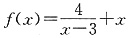
的最大值是______.
三、解答题1. 已知向量
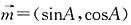
,
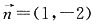
,且
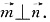
(1)求tanA的值;
(2)求函数f(x)=cos2x+tanAsinx(x∈R)的值域.
(1)
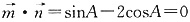
,得tanA=2.
(2)
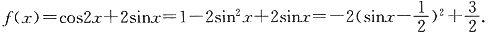
当
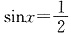
时,f(x)有最大值

;当sinx=-1时,f(x)有最小值-3.
所以f(x)的值域是
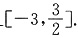
2. 设f(x)是定义在[0,1]上的函数,若存在x
*∈(0,1),使得f(x)在[0,x
*]上单调递增,在[x
*,1]上单调递减,则称f(x)为[0,1]上的单峰函数,x
*为峰点,包含峰点的区间为含峰区间,对任意的[0,1]上的单峰函数f(x),下面研究缩短其含峰区间长度的方法.
(1)证明:对任意的x
1,x
2∈(0,1),x
1<x
2,若f(x
1)≥f(x
2),则(0,x
2)为含峰区间;
若f(x
1)≤f(x
2),则(x
1,1)为含峰区间;
(2)对给定的r(0<r<0.5),证明:存在x
1,x
2∈(0,1),满足x
2-x
1≥2r,使得由(l)所
确定的含峰区间的长度不大于0.5+r.
(1)证明:设x
*为f(x)的峰点,则由单峰函数定义可知,f(x)在[0,x
*]上单调递增,在[x
*,1]上单调递减,
当f(x
1)≥f(x
2)时,假设

,则x
1<x
2<x
*,从而f(x
*)≥f(x
2)>f(x
1),这与f(x
1)≥f(x
2)矛盾,所以x
*∈(0,x
2),即(0,x
2)为含峰区间.
当f(x
1)≤f(x
2)时,假设
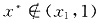
,则x
*≤x
1<x
2,从而f(x
*)≥f(x
1)>f(x
2)这与f(x
1)≤f(x
2)矛盾,所以x
*∈(x
1,1),即(x
1,1)为含峰区间
(2)证明:由(1)的结论可知:
当f(x
1)≥f(x
2)时,含峰区间的长度为l
1=x
2;
当f(x
1)≤f(x
2)时,含峰区间的长度为l
2=1-x
1;
对于上述两种情况,由题意得
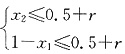
①
由①得1+x
2-x
1≤1+2r,即x
2-x
1≤2r,
又因为x
2-x
1≥2r,所以x
2-x
1=2r ②
将②代入①得x
1≤0.5-r,x
2≥0.5+r, ③
由①和③解得x
1=0.5-r,x
2=0.5+r,
所以这时含峰区间的长度l
1=l
2=0.5+r,
即存在x
1,x
2使得所确定的含峰区间的长度不大于0.5+r.
3. 已知:数列{a
n}满足
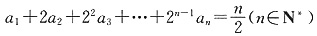
(1)求数列{a
n}的通项;
(2)若
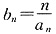
,求数列{b
n}的前n项的和S
n.
解:(1)n=1时,

,n≥2时,
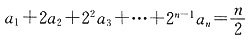
①
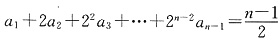
②
①-②得
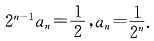
又
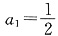
适合上式.
∴
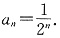
(2)b
n=n·2
n.
S
n=1·2+2·2
2+3·2
3+…+n·2
n.
2S
n=1·2
2+2·2
3+…+(n-1)·2
n+n·2
n+1.
∴(1-2)S
n=2+2
2+…+2
n-n·2
n+1 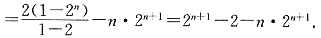
∴S
n=(n-1)2
n+1+2.
4. 如图所示,在棱长为2的正方体OABC—O
1A
1B
1C
1中,E、F分别为棱AB和BC上的动点,且AE=BF.
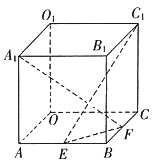
(1)求证:A
1F⊥C
1E;
(2)当O
1B⊥EF时,求点B到平面B
1EF的距离.
解:(1)建立如图所示的空间直角生标系O—xyz,设AE=t,则CF=2-t,
∴E点为(2,t,0),F(2-t,2,0).
又A
1(2,0,2),C
1(0,2,2),
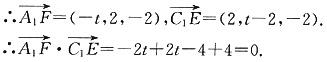
∴
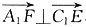
,即A
1F⊥C
1E.
(2)由(1)得O
1B=(2,2,-2),
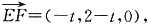
又
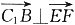
,∴-2t+4-2t=0,得t=1.
∴E、F分别为AB、BC的中点.
设点B到平面B
1EF的距离为h,由V
B-B1EF=V
B1-BEF得,
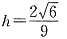
 ,且α是第四象限的角,那么cos(α-2π)的值是______.
,且α是第四象限的角,那么cos(α-2π)的值是______.
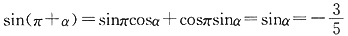 ,又α为第四象限的角,所以,
,又α为第四象限的角,所以, . 故选A.
. 故选A.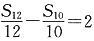 ,则S2008的值等于______.
,则S2008的值等于______. ,所以d=2,S2008=
,所以d=2,S2008=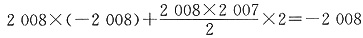 . 答案为-2008. 故选B.
. 答案为-2008. 故选B.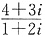 的实部是______.
的实部是______.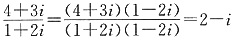 ,因此实部是2.故选B.
,因此实部是2.故选B. ,则a的值为______.
,则a的值为______.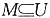 ,且
,且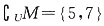 可知|a-5|=3,解得a∈{8,2}.故选D.
可知|a-5|=3,解得a∈{8,2}.故选D.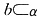 时,若b⊥β,则a⊥β
时,若b⊥β,则a⊥β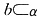 时,且c是a在α内的射影时,若b⊥c,则α⊥b
时,且c是a在α内的射影时,若b⊥c,则α⊥b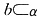 时,且
时,且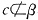 ,若c∥α,则b∥c
,若c∥α,则b∥c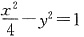 的右支上一点,M\N分别是圆
的右支上一点,M\N分别是圆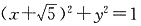 和圆(x-
和圆(x-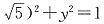 上的点,则|PM|-|PN|的最大值是______.
上的点,则|PM|-|PN|的最大值是______.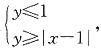 则x+2y的最大值是______.
则x+2y的最大值是______.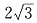 ,则a=______.
,则a=______.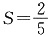 ,则球心到二面角的棱的距离为______.
,则球心到二面角的棱的距离为______.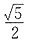
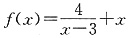 的最大值是______.
的最大值是______.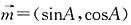 ,
,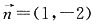 ,且
,且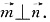
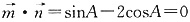 ,得tanA=2.
,得tanA=2.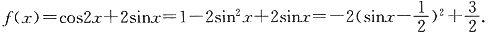
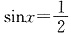 时,f(x)有最大值
时,f(x)有最大值 ;当sinx=-1时,f(x)有最小值-3.
;当sinx=-1时,f(x)有最小值-3.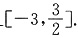
 ,则x1<x2<x*,从而f(x*)≥f(x2)>f(x1),这与f(x1)≥f(x2)矛盾,所以x*∈(0,x2),即(0,x2)为含峰区间.
,则x1<x2<x*,从而f(x*)≥f(x2)>f(x1),这与f(x1)≥f(x2)矛盾,所以x*∈(0,x2),即(0,x2)为含峰区间.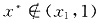 ,则x*≤x1<x2,从而f(x*)≥f(x1)>f(x2)这与f(x1)≤f(x2)矛盾,所以x*∈(x1,1),即(x1,1)为含峰区间
,则x*≤x1<x2,从而f(x*)≥f(x1)>f(x2)这与f(x1)≤f(x2)矛盾,所以x*∈(x1,1),即(x1,1)为含峰区间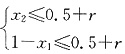 ①
①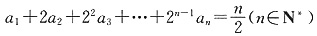
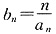 ,求数列{bn}的前n项的和Sn.
,求数列{bn}的前n项的和Sn. ,n≥2时,
,n≥2时,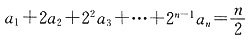 ①
①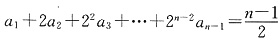 ②
②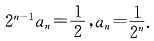
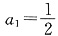 适合上式.
适合上式.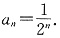
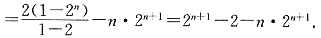

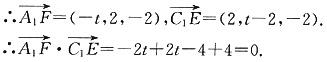
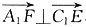 ,即A1F⊥C1E.
,即A1F⊥C1E.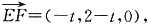
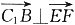 ,∴-2t+4-2t=0,得t=1.
,∴-2t+4-2t=0,得t=1.