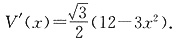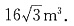一、填空题1. 德育过程的基本矛盾是教育者提出的______与受教育者已有______的矛盾.
2. 课外校外教育的组织形式有______活动、______活动、个人活动.
3. 学生的数学学习内容应当是______、______、______的,这些内容有利于学生主动地进行观察、实验、猜测、验证、推理与交流等数学活动.
4. 中学数学教学所必须遵循的四个基本原则是______、______、______、______.
严谨性与量力性相结合的原则 抽象与具体相结合的原则 理论与实际相结合的原则 巩固与发展相结合的原则
5. 选择公理的时候,应注意______、______、______的要求.
三、简答题1. 谈谈你对数学课程总体目标与具体目标关系的认识.
《国家数学课程标准》关于目标的叙述明确表明:数学课程的目标不只是让学生获得必要的数学知识、技能与数学思想方法,它还应当包括促进学生思维能力、思维水平方面,用数学解决问题能力方面,情感与态度方面的发展.目标突出了学生的发展和社会的需要,为此总体目标被细化为四个方面的具体目标:知识与技能、数学思考、解决问题、情感与态度,所以,作为实现课程目标的主要途径,数学课堂教学活动应当将这“四个方面”同时作为我们的教学目标,而不是仅仅关注其中的一个或几个方面,如知识与技能、解决问题等,或是将其中的某一目标(例如情感与态度)作为实现其他目标过程中的一个“副产品”.
另一方面,四个目标是在丰富多彩的数学活动中实现的.其中,数学思考、解决问题、情感与态度的发展离不开知识与技能的学习,而知识与技能的学习必须有利于其他目标的实现,这里包含两层意思:一是“数学思考、解决问题、情感与态度”目标的实现是通过数学知识的学习来完成的,不需要也不可能为它设置专门课程;二是学什么样的知识技能,应当首先考虑到是否有利于其他三方面的目标的实现.
2. 中学班主任的任务和职责是什么?
我国的《中学班主任工作暂行规定》对班主任任务作了明确规定.班主任的基本任务是:“按照德、智、体、美全面发展的要求,开展班级工作,全面教育、管理、指导学生,使他们成为有理想、有道德、有文化、有纪律、体魄健康的公民,”
《中学班主任工作暂行规定》对班主任的职责作了如下规定.
(1)向学生进行思想政治教育和道德教育,保护学生身心健康,教育学生热爱社会主义祖国,逐步树立为人民服务的思想和为实现社会主义现代化而奋斗的志向,培养社会主义道德品德和良好的心理品质,遵守《中学生守则》和《中学生日常行为规范>.
(2)教育学生努力完成学习任务.会同各科教师教育、帮助学生明确学习目的,端正学习态度,掌握正确的学习方法,提高学习成绩.
(3)教育、指导学生参加学校规定的各种劳动,协助学校贯彻实施《体育卫生工作条例》,教育学生坚持体育锻炼,养成良好的劳动习惯、生活习惯和卫生习惯.
(4)关心学生课外生活.指导学生参加各种有益于身心健康的科技、文娱和社会活动,鼓励学生发展正当的兴趣和特长.
(5)进行班级的日常管理.建立班级常规,指导班委会和本班的团队工作,培养学生干部,提高学生的自理能力,把班级建设成为奋发向上、团结友爱的集体.
(6)负责联系和组织科任教师商讨本班的教育工作,互通情况,协调各种活动和课业负担.
(7)做好本班学生思想品德评定和有关奖励工作.
(8)联系本班学生家长,争取家长和社会有关方面配合,共同做好学生教育工作.
四、分析题1. 在“空间与图形”的教学实施过程中,你如何体现其教育价值?
(1)“空间与图形”是学生感受图形世界的现实性和丰富多彩的载体.
(2)“空间与图形”是学生数学思维训练的好载体.
(3)“空间与图形”是数学育人的载体.
四、解答题1. 设函数
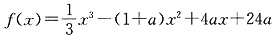
,其中常数a>1.
(1)讨论f(x)的单调性;
(2)若当x≥0时,f(x)>0恒成立,求a的取值范围.
(1)f′(x)=x
2-2(1+a)x+4a=(x-2)(x-2a),
由a>1知,当x<2时,f′(x)>0,故f(x)在区间(-∞,2)是增函数;
当2<x<2a时,f′(x)<0,故f(x)在区间(2,2a)是减函数;
当x>2a时,f′(x)>0,故f(x)在区间(2a,+∞)是增函数,
综上,当a>1时,f(x)在区间(-∞,2)和(2a,+∞)是增函数,在区间(2,2a)是减函数.
(2)由(1)知,当x≥0时,f(x)在x=2a或x=0处取得最小值,

由假设知
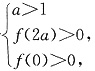
即
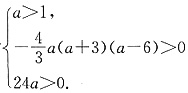
,解得1<a<6.
故a的取值范围是(1,6).
五、应用题1. “五一”假期期间,某学校计划组织385名师生租车旅游,现知道租车公司有42座和60座两种客车,42座客车的租金每辆为320元,60座客车的租金每辆为460元.
(1)若学校只租用42座客车或者只租用60座客车,那么学校各需多少租金?
(2)若学校同时租用这两种客车共8辆(可以坐不满),而且要比单独只租用一种车辆节省租金,请你帮助该学校选择一种最节省的租车方案.
(1)385÷42≈9.2,所以单独租用42座客车需10辆,租金为320×10=3200(元),385÷60≈6.4,所以单独租用60座客车需7辆,租金为460×7=3220(元).
(2)设租用42座客车x辆,则60座客车(8-x)辆,由题意得,
320x+460(8-x)≤3200,42x+60(8-x)≥385.
解得3.4≤x≤5.3.
由于x取整数,所以x=4或5.
当x=4时,租金为320×4+460×(8-4)=3120(元);
当x=5时,租金为320×5+460×(8-5)=2980(元).
故租用42座客车5辆,60座客车3辆,租金最少.
2. 工厂车间有10台同类型的机床,每台机床配备的电动机功率为10kW,已知每台机床工作时,平均每小时实际开动12分钟,且开动与否是相互独立的,现因当地电力供应紧张,供电部门只提供50kW的电力,这10台机床能够正常工作的概率为多大?在一个工作班的8小时内,不能正常工作的时间大约是多少?
设10台机床中实际开动的机床数为随机变量ξ,由于机床类型相同,且机床的开动与否相互独立,因此ξ~B(10,p).其中p是每台机床开动的概率,由题意
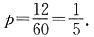
从而
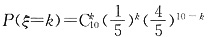
,k=0,1,2,…,10.
50kW电力同时供给5台机床开动,因而10台机床同时开动的台数不超过5台时都可以正常工作.这一事件的概率为P(ξ≤5),
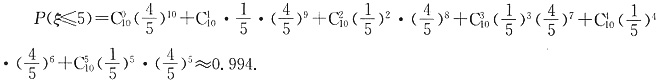
因此,在电力供应为50kW的条件下,机床不能正常工作的概率仅约为0.006,从而在一个工作班的8h内,不能正常工作的时间只有大约8×60×0.006=2.88(分钟),这说明,10台机床的工作基本上不受电力供应紧张的影响.
3. 请您设计一个帐篷,它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如下图所示),试问当帐篷的顶点O到底面中心O
1的距离为多少时,帐篷的体积最大?
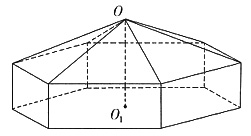
设OO
1为xm,则1<r<4,由题设可得正六棱锥底面边长为:
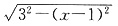
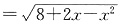
,(单位:m)
故底面正六边形的面积为
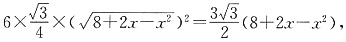
(单位:m
2)
帐篷的体积为:
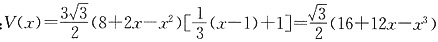
(单位:m
3)
求导得
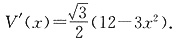
令V′(x)=0,解得x=-2(不合题意,舍去),x=2,
当1<x<2时,V′(x)>0,V(x)为增函数;
当2<x<4时,V′(x)<0,V(x)为减函数.
∴当x=2时,V(x)最大,
答:当OO
1为2m时,帐篷的体积最大,最大体积为
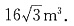
六、数学作文1. 数列是高中数学很重要的内容之一,数列中求通项的问题也是最常见的题型,其形式多样,解法灵活,请你谈谈几种常用的求数列通项的方法.
常用的求数列通项的方法有迭加法、迭乘法、换元法、倒数法、待定系数法和分类讨论等等(需要简要说明每种方法使用的情况并举例).
 的结论正确的是______.
的结论正确的是______.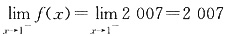 ;在x=1处的右极限为
;在x=1处的右极限为 . 故f(x)在x=1处的极限存在,且
. 故f(x)在x=1处的极限存在,且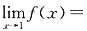 2007. 故选C.
2007. 故选C.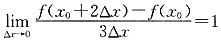 ,则导数f′(x0)等于______.
,则导数f′(x0)等于______.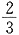 D.
D.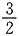
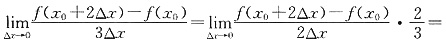
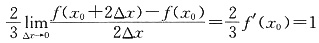 ,所以
,所以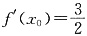 .故选D.
.故选D.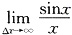 等于______.
等于______.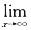
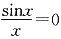 .故选A.
.故选A.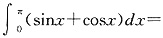 ______.
______.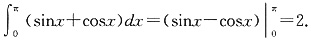 故选C.
故选C.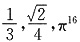 这三个实数中,分数共有______.
这三个实数中,分数共有______.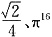 是无理数,故不是分数.故选B.
是无理数,故不是分数.故选B.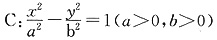 上,c的焦距为4,则它的离心率为______.
上,c的焦距为4,则它的离心率为______.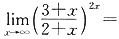 ______.
______.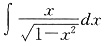
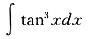
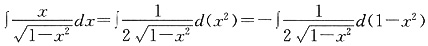
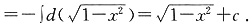
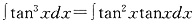
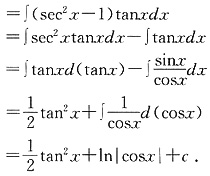
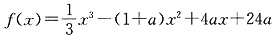 ,其中常数a>1.
,其中常数a>1.
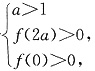 即
即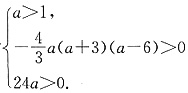 ,解得1<a<6.
,解得1<a<6.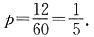
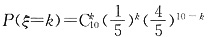 ,k=0,1,2,…,10.
,k=0,1,2,…,10.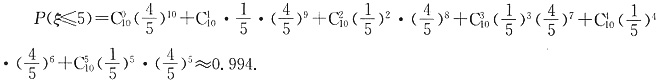

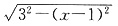
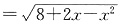 ,(单位:m)
,(单位:m)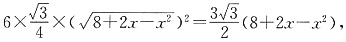 (单位:m2)
(单位:m2)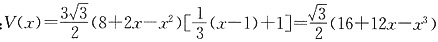 (单位:m3)
(单位:m3)