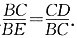一、填空题1. ______是对教育专制性、等级化和特权化的否定.
2. 教育学作为一门课程在大学里讲授,最早始于德国哲学家______.
3. 数学教学活动必须建立在学生的______和已有______的基础上,教师应激发学生的学习积极性,向学生提供充分从事数学______的机会,帮助他们在自主探索和______的过程中真正理解和掌握数学知识技能、数学思想和方法,获得广泛的数学活动经验.
4. 评价的主要目的是为了全面了解学生的数学学习历程,激励学生的学习和改进教师的教学;应建立评价目标______化、评价方法______化的评价体系,对学生的数学学习评价要关注学生数学学习的______,更要关注他们的______.
5. 初中数学新课程的四大学习领域是______、______、______、______.
实数与代数 空间与图形 统计与概率 实践与综合应用
三、论述题1. 论述人的身心发展的一般规律及其对教育的要求,
(1)人的身心发展的顺序性.
人的身心发展的顺序性是指人的身心发展是一个由低级到高级、由简单到复杂、由量变到质变的连续不断的发展过程,在这一过程中,人的身心发展不仅在整体上具有一定的顺序性,而且个别过程和特点的出现也具有一定的顺序性.
人的身心发展的顺序性规律,要求教育工作者要循序渐进地做好教育工作.循序渐进并不是消极地迁就学生的现有发展水平,而是要向学生不断提出高于现有水平又能使学生经过努力能够达到的要求,以促进学生的发展.
(2)人的身心发展的阶段性,
人的身心发展的阶段性是指个体在不同的年龄阶段表现出不同的总体特征及主要矛盾,面临着不同的发展任务.人的身心发展的每一个阶段,都经历一个由量变到质变的过程,质变意味着达到一个新的阶段.
人的身心发展的阶段性规律,决定了教育工作必须根据不同年龄阶段的特点分阶段进行.在教育教学的要求、教育教学内容和方法的选择上,不能搞“一刀切”;与此同时,还应看到各年龄阶段又是相互联系的,要注意各阶段间的衔接和过渡.
(3)人的身心发展的不平衡性.
人的身心发展的不平衡性是指个体身心发展不是一个匀速前进的过程,个体身心发展的不平衡性表现在两个方面:一是同一方面的发展速度,在不同的年龄阶段变化是不平衡的,二是不同方面发展的不平衡性,
根据人的身心不同方面有不同的发展期的现象,心理学家提出了发展关键期或最佳期的概念.教育教学工作要抓住关键期,以求在最短的时间内取得最佳的效果.
(4)人的身心发展的互补性,
人的身心发展的互补性反映个体身心发展各组成部分的相互关系,它首先指机体某一方面的机能受损甚至缺失后,可通过其他方面的超常发展得到部分补偿.
人的身心发展的互补性规律,要求教育工作者首先要树立信心,相信每一个学生,特别是暂时落后或某些方面有缺陷的学生,通过其他方面的补偿性发展,都会达到与一般正常学生一样的发展水平;其次要掌握科学的教育方法,发现学生的优势,扬长避短、长善救失,激发学生自我发展的信心和自觉.
(5)人的身心发展的个别差异性.
人的身心发展的个别差异性是指个体之间的身心发展以及个体身心发展的不同方面之间,存在着发展程度和速度的不同.个别差异首先表现在不同儿童同一方面的发展速度和水平不同.其次,个别差异表现在不同儿童不同方面的发展存在着差异,另外,个别差异表现为群体间的差异.
人的身心发展的个别差异性规律,要求教育工作者充分尊重每一个学生的个别差异,做到因材施教,使每一个学生都能获得最大限度的发展.
四、教学技能1. 写出“平面直角坐标系(第一课时)”一课的教学目标、教学重点难点、教学策略.
教学目标:
(1)知识与能力目标,
①理解有序数对,掌握平面直角系的概念.②掌握平面内的点与有序数对的一一对应关系,能熟练地在给定的直角坐标系中,根据坐标描出点的位置,能由点的位置写出点的坐标,③了解象限的概念,能根据象限内和坐标轴的特征,熟练地由点的坐标判断点在的象限.
(2)过程与方法.
①由生活事例引入,师生合作,指出有序数对可以确定物体的位置.②用有序数对确定平面内的位置,结合数轴上确定点的方法,引出平面直角坐标系学习平面直角坐标系的概念,如:横轴、纵轴、原点、坐标、象限,建立点与坐标的关系.③让学生观察地图上怎样利用坐标表示点的地理位置,使学生启发,建立坐标系的问题.
(3)情感态度与价值观.
①通过具体情境的创设,使学生在生活中发现数学问题,感受数学知识在生活中的应用,激发学习数学的兴趣.②让学生体会其中表现了数形结合的思想以及其应用价值,感受到数学是来源于生活而已用于生活的基本理念.
教学重点难点:
(1)重点.理解本节相关基本概念,能在坐标系中根据坐标找到点,由点得坐标.
(2)难点.体会其中的一一对应的关系以及各象限的坐标规律.
教学策略.以生活实例为基础,从生活中挖掘数学,并将数学应用于生活.让学生们从生活实例中体味到数学的作用.
一、单项选择题1. 若点P(2,0)到双曲线
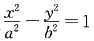
的一条渐近线的距离为
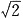
,则双曲线的离心率为______.
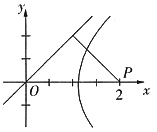

A B C D
A
[解析] 设过第一象限的渐近线倾斜角为
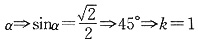
,所以y=
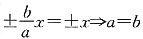
,因此

故选A.
2. “m>n>0”是“方程mx
2+ny
2=1表示焦点在y轴上的椭圆”的______.
- A.充分而不必要条件
- B.必要而不充分条件
- C.充要条件
- D.既不充分也不必要条件
A B C D
C
[解析] 要使mx
2+ny
2=1,即

是焦点在y轴上的椭圆须有
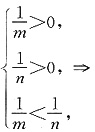
m>n>0,故为充要条件,故选C.
二、填空题1. 已知
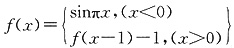
则
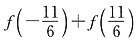
的值为______.
2. 在三棱锥P—ABC中,∠ABC=90°,∠BAC=30°,BC=5,又PA=PB=PC=AC,则点P到平面ABC的距离是______.
3. 若平面向量a、b满足|a+b|=1,a+b平行于x轴,b=(2,-1),则a=______.
4. 一个骰子连续投2次,点数和为4的概率为____.
5.
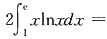
______.
6. 已知向量a=(1,2),b=(-2,3),若ka+b与a-kb垂直,则实数k的值等于______.
三、计算题1. 如图,在直三棱柱ABC—A
1B
1C
1中,AA
1=BC=AB=2,AB⊥BC,求二面角B
1—A
1C—C
1的大小.
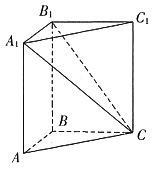
如图,建立空间直角坐标系:
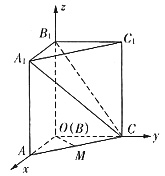
则A(2,0,0),C(0,2,0),A
1(2,0,2),B
1(0,0,2),C
1(0,2,2),
设AC的中点为M,因为BM⊥AC,BM⊥CC
1,
所以BM⊥平面A
1C
1C,
即
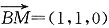
是平面A
1C
1C的一个法向量.
设平面A
1B
1C的一个法向量是n=(x,y,z).
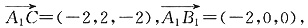
所以
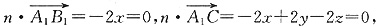
令x=1,解得x=0,y=1.
所以n=(0,1,1).
设法向量n与
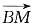
的夹角为φ,二面角B
1-A
1C-C
1的大小为θ,显然θ为锐角.
因为

,解得
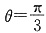
.
所以二面角B
1-A
1C-C
1的大小为
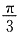
.
2. 已知复数z=a+bi(a、b∈R
+)(i是虚数单位)是方程x
2-4x+5=0的根,复数w=u+3i(u∈R)满足
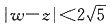
,求u的取值范围.
原方程的两个根为x
1=2+i,x
2=2-i
∵a,b∈R
*,
∴z=2+i.
∵
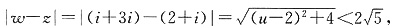
∴-2<u<6.
3. 已知
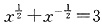
,求
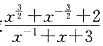
的值.
四、应用题1. 如图,A、B、C、D都在同一个与水平面垂直的平面内,B、D为两岛上的两座灯塔的塔顶,测量船于水面A处测得B点和D点的仰角分别为75°、30°,于水面C处测得B点和D点的仰角均为60°,AC=0.1km. 试探究图中B、D间距离与另外哪两点间距离相等,然后求B、D的距离(计算结果精确到0.01km,
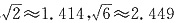
).
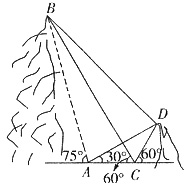
在△ACD中,∠DAC=30°,∠ADC=60°-∠DAC=30°,
所以CD=AC=0.1km,又∠BCD=180°-60°-60°=60°,
故CB是△CAD底边AD的中垂线,所以BD=BA.
在△ABC中,
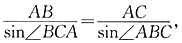
即
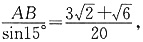
因此,
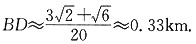
故B、D的距离约为0.33km.
六、数学作文1. 请结合实际,简要谈谈你对数学素质的一点看法.
纲要:(1)数学素质是在热爱数学、欣赏数学的基础上产生的对数学的理解能力和应用能力;(2)评价一个人的数学素质,不仅仅是从他数学考试成绩上推断,更重要的衡量标准应该是他是否能够在日常生活中准确、灵活地运用数学知识;(3)真正对数学知识准确灵活的应用,需要有对数学的敏感性;(4)要提高数学素质,绝不是多做题就可以解决的,更要有对数学的热爱.
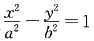 的一条渐近线的距离为
的一条渐近线的距离为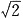 ,则双曲线的离心率为______.
,则双曲线的离心率为______.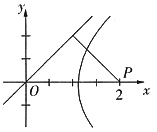

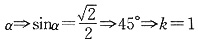 ,所以y=
,所以y=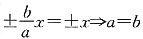 ,因此
,因此 故选A.
故选A. 是焦点在y轴上的椭圆须有
是焦点在y轴上的椭圆须有 m>n>0,故为充要条件,故选C.
m>n>0,故为充要条件,故选C.
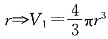 ;正三棱锥的底面面积
;正三棱锥的底面面积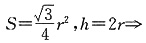
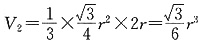 ,所以
,所以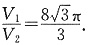 故选A.
故选A.
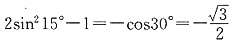 .故选A.
.故选A.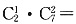 42种,另一类是甲乙都去的选法有
42种,另一类是甲乙都去的选法有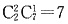 种,所以共有42+7=49种,故选C.
种,所以共有42+7=49种,故选C.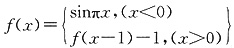 则
则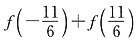 的值为______.
的值为______.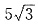
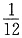
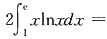 ______.
______.
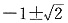


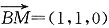 是平面A1C1C的一个法向量.
是平面A1C1C的一个法向量.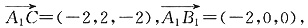
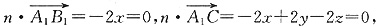
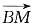 的夹角为φ,二面角B1-A1C-C1的大小为θ,显然θ为锐角.
的夹角为φ,二面角B1-A1C-C1的大小为θ,显然θ为锐角. ,解得
,解得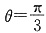 .
.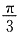 .
.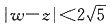 ,求u的取值范围.
,求u的取值范围.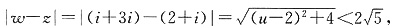
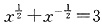 ,求
,求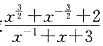 的值.
的值.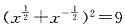 ,可得x+x-1=7
,可得x+x-1=7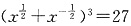
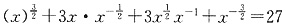
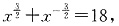
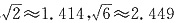 ).
).
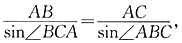
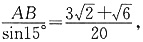 因此,
因此,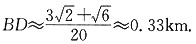
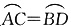 ,过C点的圆的切线与BA的延长线交于E点,证明:
,过C点的圆的切线与BA的延长线交于E点,证明: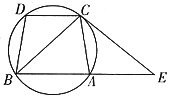
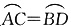 ,
,