二、填空题1. 我国教育心理学家主张学生的学习分为知识的学习、技能的学习和______的学习.
2. 桑代克认为尝试一错误学习的基本规律有:效果律、练习律和______.
3. 心理辅导的一般目标可归纳为两个方面,第一是学会调适,第二是______.
4. 教育思想具体包括______、______和______三个部分.
5. 个体发展包括______、______、______以及______等四个方面.
生理发展 人格发展 个体与他人关系的社会性发展 认识的发展
四、教学技能1. 我国的基础教育一直以来都把培养学生获取新知识的能力放在首要位置,在《基础教育课程改革纲要》中,对学生能力的培养提出了怎样的要求?
《纲要》指出要培养学生搜集和处理信息的能力,获取新知识的能力,分析和解决问题的能力以及交流与合作的能力,把培养学生搜集和处理信息的能力放在首位,符合时代的发展,体现了时代性;强调交流与合作能力,体现了学习的主动性、探究性、合作性.
一、单项选择题2. 已知△ABC中,
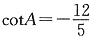
,则cosA=______.

A B C D
D
[解析]
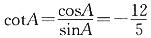
,cos
2A+sin
2A=1,由上可得
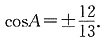
因为在三角形中角大于90°小于180°时,cos为负数,
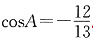
.故选D.
3. 已知向量a=(2,1),a·b=10,

,则|b|=______.
A.
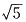
B.
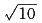
C.5 D.25
A B C D
C
[解析] 由a=(2,1)得:a
2=2
2+1
2=5,由
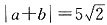
得:a
2+2ab+|b|
2=50,所以|b|
2=25,解得|b|=5. 故选C.
5. 已知正四棱柱ABCD—A
1B
1C
1D
1中,AA
1=2AB,E为AA
1中点(如图所示),则异面直线BE与CD
1所形成角的余弦值为______.
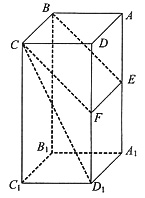

A B C D
C
[解析] 取DD
1中点F,连结CF,则CF∥BE,所以CF与CD
1所成角就是BE与CD
1所成角.设AB=1,则AA
1=2,DF=1,
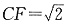
,
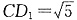
,D
1F=1.在三角形CFD
1中,根据余弦定理:
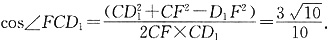
故选C.
8. 双曲线
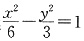
的渐近线与圆(x-3)
2+y
2=r
2(r>0)相切,则r=______.
A.

B.2
C.3 D.6
A B C D
A
[解析] 双曲线的渐近线方程为
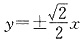
,即
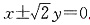
.由圆的方程可知圆心为(3,0).由圆心到直线的距离公式得
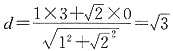
,∵双曲线的渐近线与圆相切,∴
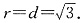
故选A.
9. 若将函数
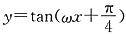
(w>0)的图像向右平移
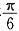
个单位长度后,与函数y=tan(wx
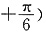
的图像重合,则w的最小值为______.

A B C D
D
[解析]
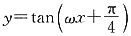
向右平移
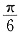
得
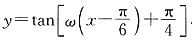
与函数y=
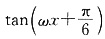
重合.由上可知:
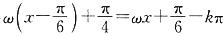
,所以
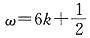
,假设w>0,则w的最小值为
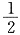
.故选D.
10. 甲、乙两人从4门课程中各选修2门,则甲、乙所选的课程中恰有1门相同的选法有______.
A B C D
C
[解析] 相同的课程是从四门中选出一门,所以是

,甲只需在剩下的三门中选一门
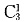
,乙必需从甲剩下的两门中选一门
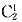
,所以甲、乙所选课程中恰有一门相同的
选法是
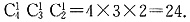
故选C.
11. 已知直线y=k(x+2)(k>0)与抛物线C:y
2=8x相交A、B两点,F为C的焦点.若|FA|=2|FB|,则k=______.

A B C D
D
[解析] 抛物线y
2=8x的准线为x=-2.直线y=k(x+2)(k>0)恒过定点P(-2,0).如下图所示过点P作直线l:x=-2,过点A、B分别作直线l的垂线,垂点为M、N.
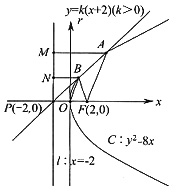
由|FA|=2|FB|得:|AM|=2|BN|.点B为AP的中点、连接OB,则
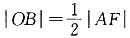
,∴|OB|=|BF|,点B的横坐标为1,故点B的坐标为
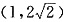
∴
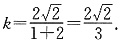
故选D.
二、填空题1. 已知圆O:x
2+y
2=5和点A(1,2),则过A且与圆O相切的直线与两坐标轴围成的三角形的面积等于______.
2. 设等比数列{A
n}的前n项和为S
n,若a
1=1,S
6=4S
3,则a
4______.
3.
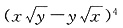
的展开式中x
3y
3的系数为______.
4. 设OA是球O的半径,M是OA的中点,过M且与OA成45°角的平面截球O的表面得到圆C.若圆C的面积等于
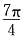
,则球O的表面积等于______.
三、解答题1. 已知等差数列{a
n}中,a
3a
7=-16,a
4+a
6=0,求{a
n}前n项和S
n.
设{a
n}的公差为d,则
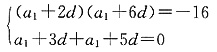
即
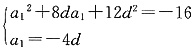
解得
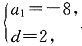
或
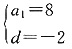
因此S
n=-8n+n(n-1)=n(n-9),或S
n=8n-n(n-1)=-n(n-9)
2. 从4名男生和2名女生中任选3人参加演讲比赛,求所选的3人中至少有1名女生的概率.
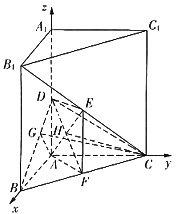
3. 如图,直三棱柱ABC—A
1B
1C
1中,AB⊥AC,D、E分别为AA
1、B
1C的中点,DE⊥平面BCC
1.

(1)证明:AB=AC;
(2)设二面角A—BD—C为60°,求B
1C与平面BCD所成的角的大小.
解法一:(1)取BC中点F,连接EF,则
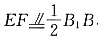
,从而
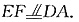
连接AF,则ADEF为平行四边形,从而AF∥DE,又DE⊥平面BCC
1,故AF⊥平面BCC
1,从而AF⊥BC,即AF为BC的垂直平分线,所以AB=AC.
(2)作AG⊥BD,垂足为G,连接CG,由三垂线定理知CG⊥BD,故∠AGC为二面角A—BD—C的平面角.由题设知,∠AGC=60°.
设AC=2,则
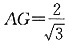
,又AB=2,
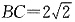
,故
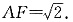
由AB·AD=AG·BD得
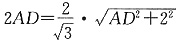
,解得
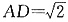
,
故AD=AF,又AD⊥AF,所以四边形ADEF为正方形.
因为BC⊥AF,BC⊥AD,AF∩AD=A,故BC⊥平面DEF,因此平面BCD⊥平面DEF.
连接AE、DF,设AE∩DF=H,则EH⊥DF,EH⊥平面BCD,
连接CH,则∠ECH为B
1C与平面BCD所成的角,
因ADEF为正方形,
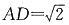
,故EH=1,又
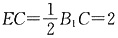
,
所以∠ECH=30°,即B
1C与平面BCD所成的角为30°.
解法二:(1)以A为坐标原点,射线AB为x轴的正半轴,建立如图所示的直角坐标系A—xyz.
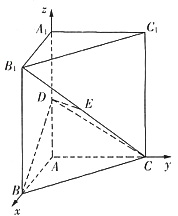
设B(1,0,0),C(0,b,0),D(0,0,c),则B
1(1,0,2c),E(
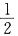
,
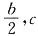
).
于是
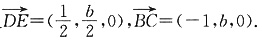
由DE⊥平面BCC
1知DE⊥BC,
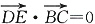
,求得b=1,所以AB=AC.
(2)设平面BCD的法向量

则
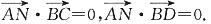
又
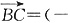
1,1,0),BD=(-1,0,c),故
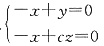
令x=1,则y=1,
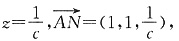
又平面ABD的法向量
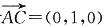
由二面角A—BD—C为60°知,

故
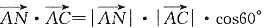
,求得
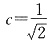
.
于是
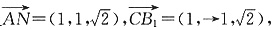
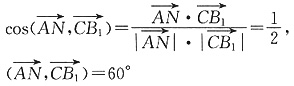
所以B
1C与平面BCD所成的角为30°.
4. 从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件A:“取出的2件产品中至多有1件是二等品”的概率为0.96.
(1)求从该批产品中任取1件是二等品的概率;
(2)若该批产品共100件,从中任意抽取2件,用ξ表示取出的2件产品中二等品的件数,求二等品件数的分布列.
(1)记A
0表示事件“取出的2件产品中无二等品”,
A
1表示事件“取出的2件产品中恰有1件二等品”,
则A
0,A
1互斥,且A=A
0+A
1,故
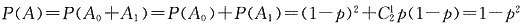
于是0.96=1-p
2,解得p
1=0.2,p
2=-0.2(舍去).
(2)ξ的可能取值为0,1,2.若该批产品共100件,由(1)知其二等品有100×0.2=20件,
故
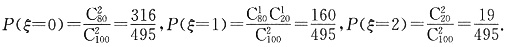
所以二等品的分布列为:
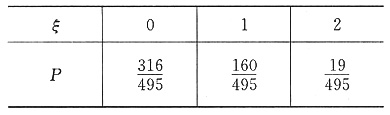
5. 设函数f(x)=-x(x-a)
2(x∈R),其中a∈R.
(1)当a=1时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)当a≠0时,求函数f(x)的极大值和极小值,
(1)当a=1时,f(x)=-x(x-1)
2=-x
3+2x
2-x,
f(2)=-2,f′(x)=-3x
2+4x-1,
f′(2)=-12+8-1=-5,
∴当a=1时,曲线y=f(x)在点(2,f(2))处的切线方程为5x+y-8=0.
(2)f(x)=-x(x-a)
2=-x
3+2ax
2-a
2x,
f′(x)=-3x
2+4ax-a
2=-(3x-a)(x-a),
令f′(x)=0,解得
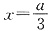
或x=a.
由于a≠0,以下分两种情况讨论,
①若a>0,当x变化时,f′(x)的正负如下表:

因此,函数f(x)在
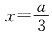
处取得极小值
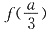
,且
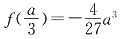
,
函数f(x)在x=a处取得极大值f(a),且f(a)=0.
②若a<0,当x变化时,f′(x)的正负如下表:

因此,函数f(x)在x=a处取得极小值f(a),且f(a)=0;
函数f(x)在
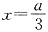
处取得极大值
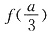
,
且
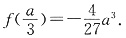
6. 已知椭圆
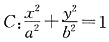
(a>6>0)的离心率为
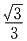
,过右焦点F的直线l与c相交于A、B两点,当l的斜率为1时,从坐标原点O到l的距离为
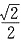
.
(1)求a,b的值;
(2)C上是否存在点P,使得当l绕F转到某一位置时
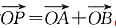
,有成立?若存在,求出所有的P的坐标与l的方程;若不存在,说明理由.
(1)设F(c,0),当l的斜率为1时,其方程为x-y-c=0,O到l的距离为

故
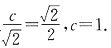
由
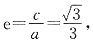
得
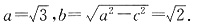
(2)C上存在点P,使得当l绕F转到某一位置时
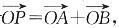
有成立
由(1)知C的方程为2x
2+3y
2=6.设A(x
1,y
1),B(x
2,y
2),
①当l不垂直x轴时,设l的方程为y=k(x-1),
C上的点P使
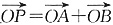
成立的充要条件是P点的坐标为(x
1+x
2,y
1+y
2),且2(x
1+x
2)
2+3(y
1+y
2)
2=6,
整理得
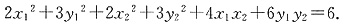
又A、B在C上,即
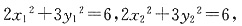
故2x
1x
2+3y
1y
2+3=0 ①
将y=k(x-1)代入2x
2+3y
2=6,并化简得
(2+3k
2)x
2-6k
2x+3k
2-6=0.
于是
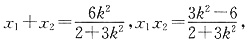
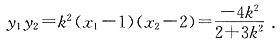
代入①解得,k
2=2,此时
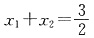
.
于是

,即
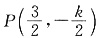
.
因此,当
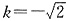
时,
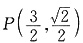
,l的方程
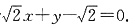
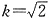
时,
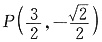
,l的方程为
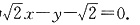
②当l垂直于x轴时,由

知,C上不存在点P使
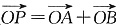
成立,
综上,C上存在点
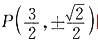
使
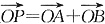
成立,此时l的方程为

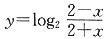 的图像______.
的图像______.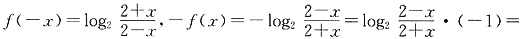
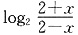 ,由上可得f(-x)=-f(x),该函数是奇函数,关于原点对称.故选A.
,由上可得f(-x)=-f(x),该函数是奇函数,关于原点对称.故选A.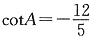 ,则cosA=______.
,则cosA=______.
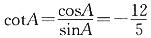 ,cos2A+sin2A=1,由上可得
,cos2A+sin2A=1,由上可得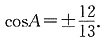 因为在三角形中角大于90°小于180°时,cos为负数,
因为在三角形中角大于90°小于180°时,cos为负数,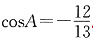 .故选D.
.故选D. ,则|b|=______.
,则|b|=______.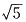 B.
B.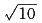
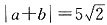 得:a2+2ab+|b|2=50,所以|b|2=25,解得|b|=5. 故选C.
得:a2+2ab+|b|2=50,所以|b|2=25,解得|b|=5. 故选C.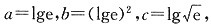 则______.
则______.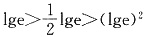 ,所以a>c>b.故选B.
,所以a>c>b.故选B.

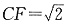 ,
,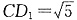 ,D1F=1.在三角形CFD1中,根据余弦定理:
,D1F=1.在三角形CFD1中,根据余弦定理: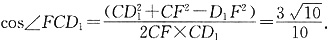 故选C.
故选C.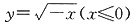 的反函数是______.
的反函数是______.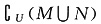 =______.
=______.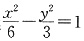 的渐近线与圆(x-3)2+y2=r2(r>0)相切,则r=______.
的渐近线与圆(x-3)2+y2=r2(r>0)相切,则r=______. B.2
B.2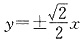 ,即
,即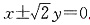 .由圆的方程可知圆心为(3,0).由圆心到直线的距离公式得
.由圆的方程可知圆心为(3,0).由圆心到直线的距离公式得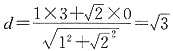 ,∵双曲线的渐近线与圆相切,∴
,∵双曲线的渐近线与圆相切,∴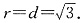 故选A.
故选A.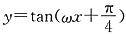 (w>0)的图像向右平移
(w>0)的图像向右平移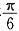 个单位长度后,与函数y=tan(wx
个单位长度后,与函数y=tan(wx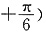 的图像重合,则w的最小值为______.
的图像重合,则w的最小值为______.
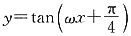 向右平移
向右平移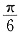 得
得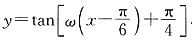 与函数y=
与函数y=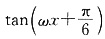 重合.由上可知:
重合.由上可知: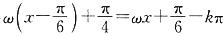 ,所以
,所以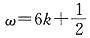 ,假设w>0,则w的最小值为
,假设w>0,则w的最小值为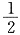 .故选D.
.故选D. ,甲只需在剩下的三门中选一门
,甲只需在剩下的三门中选一门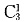 ,乙必需从甲剩下的两门中选一门
,乙必需从甲剩下的两门中选一门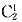 ,所以甲、乙所选课程中恰有一门相同的
,所以甲、乙所选课程中恰有一门相同的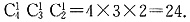 故选C.
故选C.

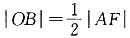 ,∴|OB|=|BF|,点B的横坐标为1,故点B的坐标为
,∴|OB|=|BF|,点B的横坐标为1,故点B的坐标为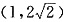 ∴
∴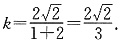 故选D.
故选D.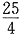
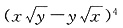 的展开式中x3y3的系数为______.
的展开式中x3y3的系数为______.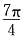 ,则球O的表面积等于______.
,则球O的表面积等于______.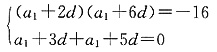
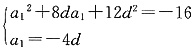
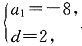 或
或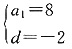
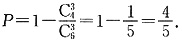

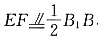 ,从而
,从而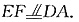

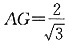 ,又AB=2,
,又AB=2,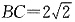 ,故
,故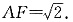
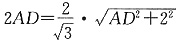 ,解得
,解得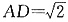 ,
,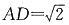 ,故EH=1,又
,故EH=1,又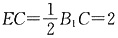 ,
,
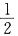 ,
,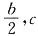 ).
).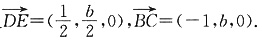 由DE⊥平面BCC1知DE⊥BC,
由DE⊥平面BCC1知DE⊥BC,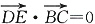 ,求得b=1,所以AB=AC.
,求得b=1,所以AB=AC. 则
则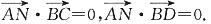 又
又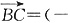 1,1,0),BD=(-1,0,c),故
1,1,0),BD=(-1,0,c),故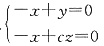
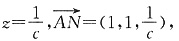
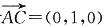

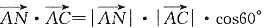 ,求得
,求得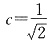 .
.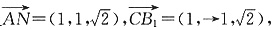
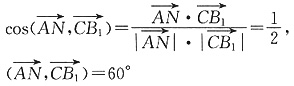
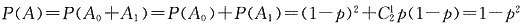
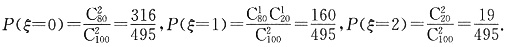

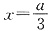 或x=a.
或x=a.
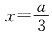 处取得极小值
处取得极小值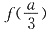 ,且
,且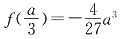 ,
,
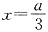 处取得极大值
处取得极大值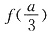 ,
,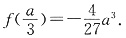
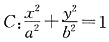 (a>6>0)的离心率为
(a>6>0)的离心率为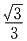 ,过右焦点F的直线l与c相交于A、B两点,当l的斜率为1时,从坐标原点O到l的距离为
,过右焦点F的直线l与c相交于A、B两点,当l的斜率为1时,从坐标原点O到l的距离为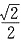 .
.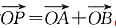 ,有成立?若存在,求出所有的P的坐标与l的方程;若不存在,说明理由.
,有成立?若存在,求出所有的P的坐标与l的方程;若不存在,说明理由.
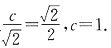
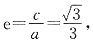
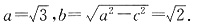
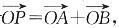 有成立
有成立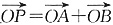 成立的充要条件是P点的坐标为(x1+x2,y1+y2),且2(x1+x2)2+3(y1+y2)2=6,
成立的充要条件是P点的坐标为(x1+x2,y1+y2),且2(x1+x2)2+3(y1+y2)2=6,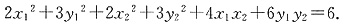
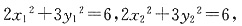
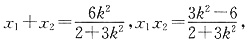
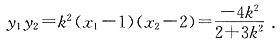
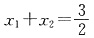 .
. ,即
,即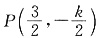 .
.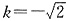 时,
时,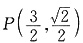 ,l的方程
,l的方程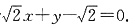
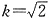 时,
时,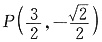 ,l的方程为
,l的方程为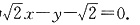
 知,C上不存在点P使
知,C上不存在点P使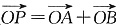 成立,
成立,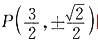 使
使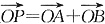 成立,此时l的方程为
成立,此时l的方程为
