单项选择题 1. 设直线的方程为
,则直线:
A.过点(1,-1,0),方向向量为2i+j-k B.过点(1,-1,0),方向向量为2i-j+k C.过点(-1,1,0),方向向量为-2i-j+k D.过点(-1,1,0),方向向量为2i+j-k
A
设直线L过点M
0 (x
0 ,y
0 ,z
0 ),它的一个方向向量为s={m,n,p},则直线L的方程为
此方程称为直线的对称式方程。
如设参数t如下:
则
此方程组称为直线的参数式方程
2. 设平面π的方程为2x-2y+3=0,以下选项中错误的是:
(A) 平面π的法向量为i-j
(B) 平面π垂直于z轴
(C) 平面π平行于z轴
(D) 平面π与xoy面的交线为
B
平面的方程
设平面Ⅱ过点M
0 (x
0 ,y
0 ,Z
0 ),它的一个法向量n=|A,B,C|,则平面Ⅱ的方程为
A(x-x
0 )+B(y-y
0 )+C(z-z
0 )=0,
此方程称为平面的点法式方程
平面的一般方程为
Ax+By+Cz+D=0,
其中n=|A,B,C|为该平面的注向量
设一平面与x、y、z轴分别交于P(a,0,0),Q(0,b,0)和R(0,0,c)三点(其中a≠0,b≠0,c#0),则该平面的方程为
此方程称为平面的截距式方程,a、b、c依次称为平面在x、y、z轴上的截距,
对于一些特殊的三元一次方程,应该熟悉它们的图形的特点。
如,在方程
Ax+By+Cz+D=0
中,当D=0时,方程表示一个通过原点的平面;当A=0时,方程表示一个平行于x轴的平面;当A=B=0时,方程表示一个平行于xOy面的平面,类似地,可得其他情形的结论。
4. 若有
,则当x→0时,f(x)是:
A.有极限的函数 B.有界函数 C.无穷小量 D.比(x-a)高阶的无穷小
D
①若
,就称β是比α高阶的无穷小,记作β=0(α),并称α是比β低阶的无穷小。
②若
,就称β是与α同阶的无穷小。
③若
,就称β是与α等价的无穷小,记作α~β。
关于等价无穷小。有以下性质:
若a~α',β~β',且
存在,则
当x→0时,有以下常用的等价无穷小;
8. 对于曲线
,下列各性态不正确的是:
A.有3个极值点 B.有3个拐点 C.有2个极值点 D.对称原点
A
y'=x
4 -x
2 =x
2 (x
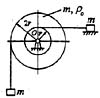
2 -1)=0,得x=-1,0,1。
验证这3个点是否都是极值点,
x=0_和x=0
+ 时,y'均小于0,即符号相同,则点(0,0)不是极值点;
x=-1
- 和x=-1
+ 时,y'符号不同,则点
为极值点;
同理,点
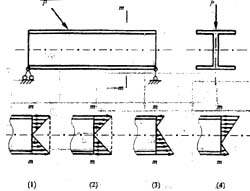
为极值点
即有2个极值点,所以选项(A)错误。
画图如下,可看出有2个极佰点。
y"=(x
4 -x
2 )'=4x
3 -2x=2x(2x
2 -1)=0,得
,和上面一样进行验证后知这三个均为拐点。
因为y是奇函数,所以对称原点。
[点评] 导数为0并不一定就是极值点,必须进行验证。
16. 微分方程cos ydx+(1+e
-x )sin ydy=0满足初始条件y
x=0 =
的特解是:
(A) cosy=
(1+e
x ) (B) cosy=(1+e
x )
(C) cos y=4(1+e
x ) (D) cos
2 y=(1+e
x )
A
此为可分离变量的方程,将变量分离得
,即
,两边积分,
ln(1+e
x )=ln(cos y)+c
1 ,
,将x=0,
代入,得c=4。
20. 离散型随机变量X的分布为P(X=k)=cλ
k (k=0,1,2,…),则不成立的是:
(A) c>0 (B).0<λ<1
(C) c=1-λ (D)
D
因为概率总非负,所以cλ
k ≥0,所以c≥0,但是如果c=0,则
p(X=0)+p(X=1)+P(X=2)+…=0≠1,显然不对,因此c≠0,得c>0。
P(X=0)+P(X=1)+P(X=2)+…=c(1+λ+λ
2 +…)=
,则0<λ<1,上式变为
,得c=1-λ。所以选项(B)、(C)正确,(D)错误。
[点评]
24. 设β
1 ,β
2 是线性方程组Ax=b的两个不同的解,α
1 、α
2 是导出组Ax=0的基础解系,k
1 、k
2 是任意常数,则Ax=b的通解是:
C
由β
1 ,β
2 是线性方程组Ax=b的解,则Aβ
1 =b,Aβ
2 =b,得
,所以
也是线性方程组Ax=b的解。
由α1
,α
2 是线性方程组Ax=0的解,则Aα
1 =0,Aα
2 =0,得A(α
1 -α
2 )=0,因此α
1 -α
2 是Ax=0的解。
线性方程组Ax=0的通解为k
1 α
1 +k
2 (α
1 -α
2 )。
26. 容器内储有一定量的理想气体,若保持容积不变,使气体的温度升高,则分子的平均碰撞频率
和平均自由程
的变化情况为:
A
因为容器封闭,且容积不变,则单位体积分子数n不变。分子的平均自由程为
因此
不变。
由压强P=nkT,n不变,T升高,则压强p升高。分子平均碰撞频率
其中
变大,则分子平均碰撞频率
增大。
33. 在双缝干涉实验中,当入射单色光的波长减小时,屏幕上干涉条纹的变化情况是:
A.条纹变密并远离屏幕中心 B.条纹变密并靠近屏幕中心 C.条纹变宽并远离屏幕中心 D.条纹变宽并靠近屏幕中心
B
当波长减小时,明暗条纹的位置要向屏幕中心靠拢。
因为条纹间距
,λ变小,则条纹间距也变密。
[点评]
屏幕上明暗条纹位置为
k=0的明纹称为零级明纹,k=1的明纹称为1级明纹,k=1的暗纹为1级暗纹,余类推。条纹间距(相邻两明纹或相邻两暗纹之间的距离)为
显然,干涉条纹是等间距分布的。
白光照射时,中央明纹呈白色,其余各级明条纹部是由紫而红的彩色条纹。
35. 如果两个偏振片堆叠在一起,且偏振化方向之间夹角为30°。假设二者对光无吸收,光强为I
0 的自然光垂直入射在偏振片上,则出射光强为:
D
第一个偏振片为起偏振器,自然光通起偏振器后成为偏振光,光强为自然光强度的1/2,
即
由马吕斯定律,
。
[点评] 光强为I
0 的偏振光,透过检偏振器后,透射光的强度(不考虑吸收)为I=I
0 cos
2 α,其中α是起偏振器和检偏振器两个偏振化方向之间的夹角。
39. 下列分子中,键角最大的是:
C
概念题,BeCι
2 分子呈直线形,键角为180°,为最大。
[点评] 常见分子构型如下,需记忆。
sp杂化:分子呈直线形,如BeCι
2 ,H
g Cι
2 ,CO
2 ,C
2 H
2 ,
;
sp
2 杂化:分子呈平面三角形,如BF
3 ,BCι
3 ,
;
sp
3 杂化:分子呈四面体形,如CH
4 ,S
i Cι
4 ,CCι
4 ;
sp
3 不等性杂化:
41. 己知
。用广泛pH试纸测定0.10mol·dm
-3 氨水溶液的pH值约是:
D
由NH
3 ·H
2 O=NH
4 + +OH
- ,得
,
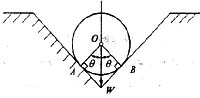
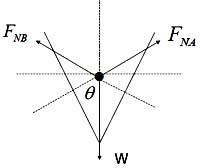
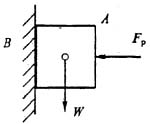
50. 重W的圆球置于光滑的斜槽内。右侧斜面对球的约束力F
NB 的大小为:
A
对物体做受力分析,画图如下,
垂直方程受力平衡,则F
NA cosθ+F
NB cosθ=W,又F
NA =F
NB ,得
56. 单摆由长ι的摆杆与捶锤A组成,其运动规律φ=φ
0 sin ωt。锤A在
秒的速度、切向加速度与法向加速度分别为:
C
速度
法向加速度大小
,方向指向圆心。
切向加速度
。
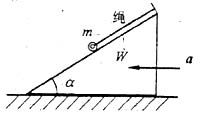
61. 两重物的质量均为m,分别系在两软绳上,此两绳又分别绕在半径各为r与2r并固结一起的两圆轮上。两圆轮构成之鼓轮的质量亦为m,对轴O的回转半径为ρ
o 。两重物中一铅垂悬挂,一置于光滑平面上,当系统在左重物重力作用下运动时,鼓轮的角加速度α为:
A
均匀细直杆对一端的转动惯量:
均匀细直杆对垂直与杆的中心轴的转动惯量:
匀质圆板对垂直于板的中心轴的转动惯量:
惯性半径:Jx=mρ
2 ;
作受力分析,下降的重物:mg-T
1 =ma
1 ,水平方向上的重物:T
2 =ma
2 ;又a
1 =2ar,a
2 =ar。再根据动量矩定理,联列以上方程得选项(A)。
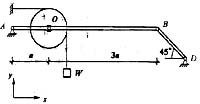
70. 已知图示二梁的抗弯截面刚度EI相同,若二者自由端的挠度相等,则P
1 /P
2 等于;
C
自由端的桡度
,W相同,则P
1 /P
2 =8。
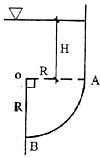
79. 图示弧形闸门AB(1/4图),闸门宽4m,圆弧半径R=1m,A点以上的水深H=1.4m,水面为大气压强。该闸门AB上静水总压力的水平分力Rx为;
A.54.88kN B.112.9kN C.91.08kN D.74.48kN
D
总压力的水平分力P
x =ρgh
c A
x ,其中A
x 为该曲面的垂直投影面积,A
x =4×1=4m
2 ,
形心
,得水平分力
P
x =ρgh
c A
x =10
3 ×9.8×1.9×4=74.48kN。
82. 变直径圆管流,细断面直径d
1 ,租断面直径d
2 =2d
1 ,粗细断面雷诺数的关系是:
A.Re1 =0.5Re2 B.Re1 =Re2 C.Re1 =1.5Re2 D.Re1 =2Re2
D
雷诺数
,又流量
,得
,流量相同,则雷诺数Re与管径d成反比。
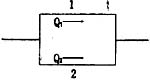
85. 长管并联管段1,2,两管段长度ι相等,直d
1 =2d
2 ,沿程阻力系数相等,则两管段的流量比Q
1 /Q
2 :
B
并联管路的水力关系为h
f1 =h
f2 ,即
,得
(因为两管长度ι
1 =ι
2 )。
又比阻
,因此
。
[点评] 并联曾路计算斋满足能量方程和连续性方程,其水力关糸为:
(1) h
f1 =h
f2 =…=h
fn ,并联管路总的能量损失等于各支路的能量损失。
(2)
,即总管支流等于各支管流量之和。
87. 用完全潜水井进行抽水实验计算渗透系数k,两位工程师各按一种经验公式选取影响半径R。分别为R
1 -3000r
0 ,R
2 =200r
0 ;其他条件相同,则计算结果k
1 /k
2 为:
D
潜水完全井产水公式为
,则
。
94. 阅读以下FORTRAN程序:
K1=M(5)
K2=M(K1)
K3=M(K1)+M(K2)
K4=M(K1+K2+K3)
WRITE(*,100)K4
100 FORMAT(2X,'K4'=',I3)
END
FUNCTION M(N)
M=N+1
RETURN
END
程序的输出结果是:
A.K4=28 B.K4=27 C.K4=30 D.K4=29
95. 阅读下列FORTRAN程序:
INTEGER X(7)
DATA X/4,5,7,8,10,12,11/
DO 10K=1,7
IF(MOD(X(K),2).NE.0)THEN
S=S+X(K)
N=N+1
END IF
10 CONTINUE
T=S/N
WRITE(*.20)S,T
20 FORMAT(2X,3F6.1)
END
程序运行后的输出结果是:
A.23.0 7.7 B.47.0 6.7 C.34.0 8.5 D.57.0 11.4
96. 下面的子程序求一方阵的次对角线上的元素之和。
SUBROUTINE CDJX(M,N,K)
DIMENSION M(N,50)
DO 10 J=1,N
K=______
10 CONTINUE
RETURN
END
为了使程序完整,应在______处填入的是:
A.K+M(J,J) B.K+M(J,N+1-J) C.K+M(N-J,J) D.K+M(N+J,N-J)
97. 阅读FORTRAN程序:
OPEN(8,FILE='FILE2
+ DA'T',STATUS='NEW')
DO 10 I=1,3
WRITE(8,'(414)')(J+I,J=1,4)
10 CONTINUE
CLOSE(8)
END
程序运行后。数据文件FILE2.AT的内容是:
A.2 3 4 5 B.1 2 3 4 C.1 2 3 4 D.1 1 1 1
98. 阅读FOKFKAN程序:
READ(*,*)N
DO 10 K-1,N
A=S+K**2
10 CONTINUE
WRITE(*,100)S
100 FORMAT(2X,F8.0)
END
键盘输入5则程序运行后的辅出结果是:
99. 设真空中点电荷+q
1 和点电荷+q
2 相距2a,且q
2 =2q
1 。以+q
1 为中心、a为半径形成封闭球面,则通过该球面的电通量为:
C
高斯定理:穿过任意封闭曲面的电通量仅与被球面包围的点电荷有关,且与半径r无关,与球外电荷也无关,等于该面积所包围的所有电荷的代数和除以ε0 。
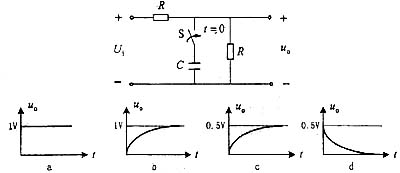
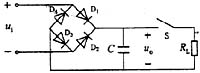
104. 圈示电路中,R=1kΩ,C=1μF,U
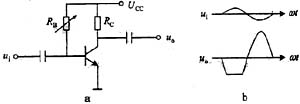
i =1V,电容无初始储能,如果开关S在t=0时刻闭合,则培出输出电压波形的是:
C
(1) 由于电容电压不能突变,则u
C (0
+ )=u
C (0
- )=0;
(2)
;
因此选(C)。
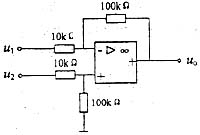
109. 运算放大器应用电路如图所示,在运算放大器线性工作区,输出电压与输入电压之间的运算关系是:
A.uo =10(u1 -u2 ) B.uo =10(u2 -u1 ) C.uo =-10u1 -11u2 D.uo =10u1 -11u2
B
又理想运放的“虚短”和“虚断”知,
,
,因为u
+ =u_,所以u
o =10(u
2 -u
1 )。
115. 某项目财务现金流量如下表,则该项目的静态投瓷回收期为多少年?
时间
1
2
3
4
5
6
7
8
9
10
净现金流量
-1200
-1000
200
300
500
500
500
500
500
500
C
静态投资回收期:P
t =累计净现金流量开始出现正值的年份数
。
项目净现金流量表如下:
时间
1
2
3
4
5
6
7
8
9
10
净现金流量
-1200
-1000
200
300
500
500
500
500
500
500
累计净现金流量
-1200
-2200
-2000
-1700
-1200
-700
-200
300
800
1300
由上表可知,累计净现金流量开始出现正值的年份数为8,
上年累计净现金流量的绝对值200,当年净现金流量为500,则
。
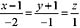 ,则直线:
,则直线: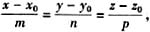
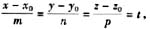
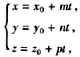
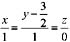
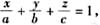
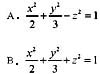
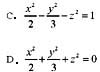

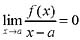 ,则当x→0时,f(x)是:
,则当x→0时,f(x)是: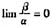 ,就称β是比α高阶的无穷小,记作β=0(α),并称α是比β低阶的无穷小。
,就称β是比α高阶的无穷小,记作β=0(α),并称α是比β低阶的无穷小。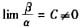 ,就称β是与α同阶的无穷小。
,就称β是与α同阶的无穷小。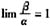 ,就称β是与α等价的无穷小,记作α~β。
,就称β是与α等价的无穷小,记作α~β。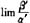 存在,则
存在,则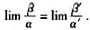
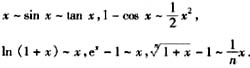
 在x处的微分是:
在x处的微分是:
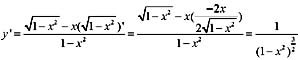
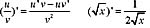
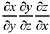 等于:
等于: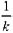
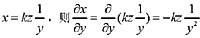 (此时把Z看做常数,对y求偏导);
(此时把Z看做常数,对y求偏导);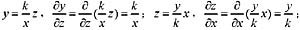
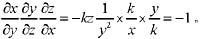
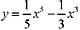 ,下列各性态不正确的是:
,下列各性态不正确的是: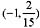 为极值点;
为极值点;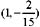 为极值点
为极值点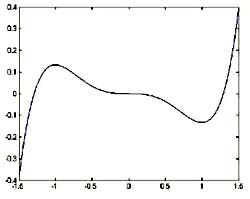
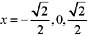 ,和上面一样进行验证后知这三个均为拐点。
,和上面一样进行验证后知这三个均为拐点。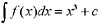 ,则
,则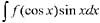 等于:(式中c为任意常数)
等于:(式中c为任意常数)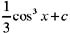
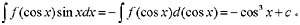
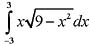 等于:
等于: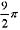
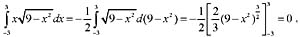
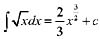
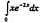 等于:
等于:
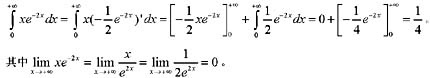
 等于:
等于:
 则
则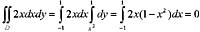
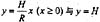 及y轴所围图形绕y轴旋转一周所得旋转体的体积为:(H,R为任意常数)
及y轴所围图形绕y轴旋转一周所得旋转体的体积为:(H,R为任意常数)
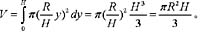

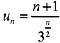 ,
,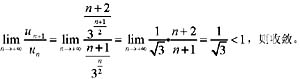
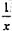 展开成(x-2)的幂级数是:
展开成(x-2)的幂级数是: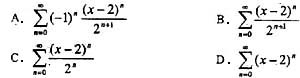
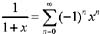 得到启发,
得到启发,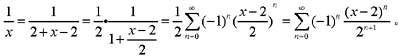
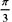 的特解是:
的特解是: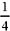 (1+ex) (B) cosy=(1+ex)
(1+ex) (B) cosy=(1+ex)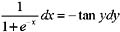 ,即
,即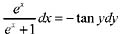 ,两边积分,
,两边积分,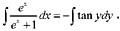 ln(1+ex)=ln(cos y)+c1,
ln(1+ex)=ln(cos y)+c1,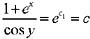 ,将x=0,
,将x=0,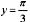 代入,得c=4。
代入,得c=4。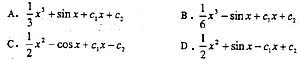
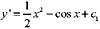 ,再次积分得
,再次积分得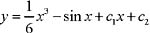 。
。
 ,则
,则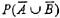 等于:
等于: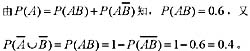

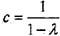
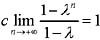 ,则0<λ<1,上式变为
,则0<λ<1,上式变为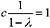 ,得c=1-λ。所以选项(B)、(C)正确,(D)错误。
,得c=1-λ。所以选项(B)、(C)正确,(D)错误。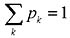

 ,Aij表示行列式元素aij的代数余子式,则A13+4A33+A43等于
,Aij表示行列式元素aij的代数余子式,则A13+4A33+A43等于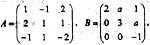 则秩r(AB-A)等于:
则秩r(AB-A)等于: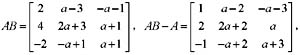
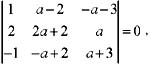 某个二介子式
某个二介子式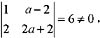 因此r(AB-A)=2。
因此r(AB-A)=2。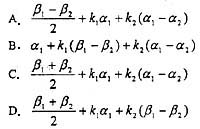
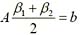 ,所以
,所以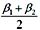 也是线性方程组Ax=b的解。
也是线性方程组Ax=b的解。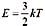 ,只与温度有关。因为温度不变,所以分子平均平动动能相同。漏气,则单位体积分子数减少,气体的内能
,只与温度有关。因为温度不变,所以分子平均平动动能相同。漏气,则单位体积分子数减少,气体的内能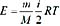 也减少。
也减少。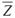 和平均自由程
和平均自由程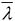 的变化情况为:
的变化情况为:
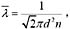 因此
因此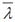 不变。
不变。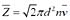 其中
其中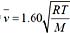 变大,则分子平均碰撞频率
变大,则分子平均碰撞频率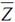 增大。
增大。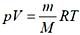 ,密度
,密度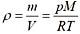 。
。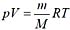
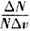 的极限就成为v的一个连续函数,这个函数叫做气体分子速率分布函数,用f(v)表示,即
的极限就成为v的一个连续函数,这个函数叫做气体分子速率分布函数,用f(v)表示,即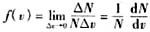


 ,λ变小,则条纹间距也变密。
,λ变小,则条纹间距也变密。
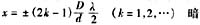
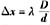
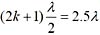 ,得k=1。
,得k=1。
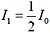 由马吕斯定律,
由马吕斯定律,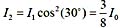 。
。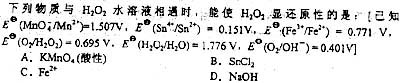
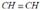 ;
;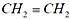 ;
;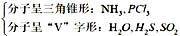
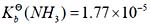 。用广泛pH试纸测定0.10mol·dm-3氨水溶液的pH值约是:
。用广泛pH试纸测定0.10mol·dm-3氨水溶液的pH值约是: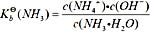 ,
,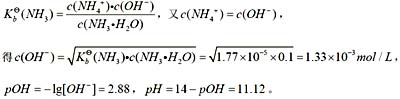
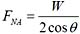
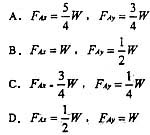
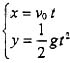 式中,t为时间,v0、g为常数。点的运动轨迹应为:
式中,t为时间,v0、g为常数。点的运动轨迹应为: ,为抛物线。
,为抛物线。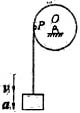
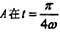 秒的速度、切向加速度与法向加速度分别为:
秒的速度、切向加速度与法向加速度分别为: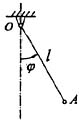

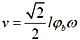
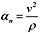 ,方向指向圆心。
,方向指向圆心。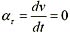 。
。

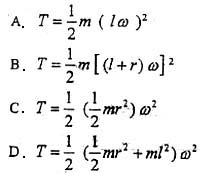
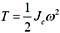 ,其中JC为刚体通过质心且垂直于运动平面的轴的转动惯量。
,其中JC为刚体通过质心且垂直于运动平面的轴的转动惯量。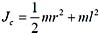 ,代入动能表达式,选(D)。
,代入动能表达式,选(D)。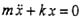 ,则描述运动的坐标Ox的坐标原点应为:
,则描述运动的坐标Ox的坐标原点应为: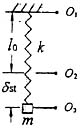

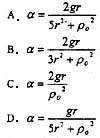
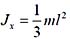
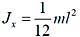
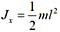

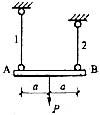


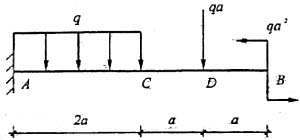
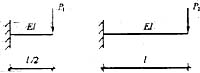
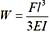 ,W相同,则P1/P2=8。
,W相同,则P1/P2=8。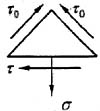
 ,比较三看的大小,则:
,比较三看的大小,则:

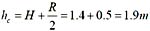 ,得水平分力
,得水平分力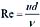 ,又流量
,又流量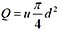 ,得
,得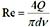 ,流量相同,则雷诺数Re与管径d成反比。
,流量相同,则雷诺数Re与管径d成反比。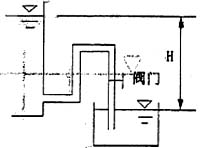
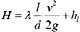 ,得
,得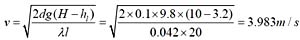 。
。
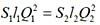 ,得
,得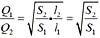 (因为两管长度ι1=ι2)。
(因为两管长度ι1=ι2)。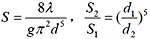 ,因此
,因此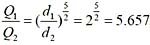 。
。 ,即总管支流等于各支管流量之和。
,即总管支流等于各支管流量之和。
 ,谢才系数
,谢才系数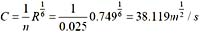 。
。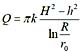 ,则
,则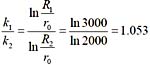 。
。
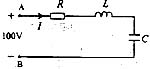
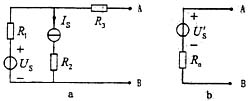

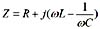 ,发生串联谐振,则虚部为0
,发生串联谐振,则虚部为0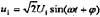 时,电感元件上的响应电压uL的韧相位为:
时,电感元件上的响应电压uL的韧相位为: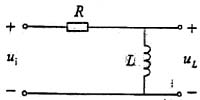
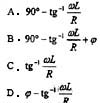
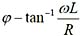 ,因为电感电压的相位超前电流90°,所以电感上的初相位为
,因为电感电压的相位超前电流90°,所以电感上的初相位为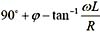 。
。
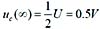 ;
;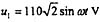 时,
时,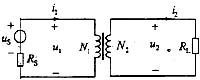
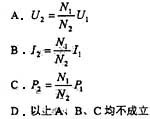
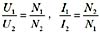
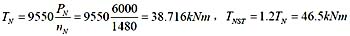 ,
,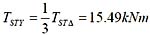 。
。
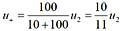 ,
, ,因为u+=u_,所以uo=10(u2-u1)。
,因为u+=u_,所以uo=10(u2-u1)。
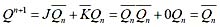 。
。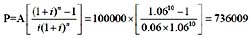 。
。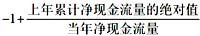 。
。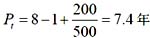 。
。