二、填空题1. 弗洛伊德的人格理论强调人是受潜意识的______驱动的,______决定个人今后的命运.
2. 教学手段就是指教师和学生进行______以及相互传递信息的工具、媒体或设备.
3. 启发学生数学学习的关键有以下几个词:______、______、______、______.
4. 数学活动是______、______的过程.
5. 学校文化的功能主要体现在______、______、______和______等四个方面.
6. 我国采用班级授课制,始于清代同治元年(1862年)于北京开办的______.
7. 美国行为主义心理学家______曾经说过,给他一打健康的婴儿,不管他们祖先的状况如何,他可以任意把他们培养成从领袖到小偷等各种类型的人.
8. 中学阶段是理想、动机和兴趣形成与发展的重要阶段,是世界观从萌芽到形成的重要阶段,是______和行为选择的重要阶段.
9. 个体发展包括______、______、______以及______等四个方面.
生理发展 人格发展 个体与他人关系的社会性发展 认识的发展
10. 原型内化的教学要求之一是活动在言语水平上先______,以后再______.
一、选择题3. 若将函数

的图像向右平移

个单位长度后,与函数

的图像重合,则ω的最小值为( ).

A B C D
D
[解析]

向右平移

得

,与函数

重合.由上可知:

,所以

,假设ω>0,则ω的最小值为

.故选D.
5. 已知△ABC中,
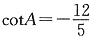
,则cosA=______.

A B C D
D
[解析]
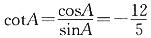
,cos
2A+sin
2A=1,由上可得
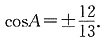
因为在三角形中角大于90°小于180°时,cos为负数,
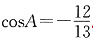
.故选D.
二、填空题1. 设OA是球O的半径,M是OA的中点,过M且与OA成45°角的平面截球O的表面得到圆C.若圆C的面积等于

,则球O的表面积等于______.
2. 已知向量a=(1,2),b=(-2,3),若ka+b与a-kb垂直,则实数k的值等于______.
3.

4. 过点A(1,0)作倾斜角为
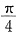
的直线,与抛物线y
2=2x交于M、N两点,则|MN|______.
5. 100个人参加某公司的招聘考试,考试内容共有5道题,1~5题分别有80人、92人、86人、78人和74人答对,答对了3道和3道以上的人员能通过考试,那么至少有______人能通过考试。
70
未答对的题目总数为(100-80)+(100-92)+(100-86)+(100-78)+(100-74)=90,由于必须答错3道或3道以上题目才不能通过考试,最不理想的情况是刚好每个人错3道,30个人正好错90道,所以至少有70个人能通过这次考试。
三、计算题1. 某商场购进一批单价为16元的日用品,经试验发现,若按每件20元的价格销售时,每月能卖360件,若按每件25元的价格销售时,每月能卖210件,假定每月销售件数y
(件)是价格x(元/件)的一次函数.
(1)试求y与x之间的关系式;
(2)在商品不积压,且不考虑其他因素的条件下,问销售价格定为多少时,才能使每月获得最大利润?每月的最大利润是多少?
依题意设y=kx+b,则有
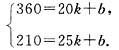
解得是k=30,b=960.
∴y=-30x+960(16≤x≤32).
(2)每月获得利润P=(-30x+960)(x-16)=30(-x
2+48x-512)=-30(x-24)
2+1920.
∴当x=24时,P有最大值,最大值为1920.即当价格为24元,每月才能获得最大利润1920元.
2. 已知椭圆
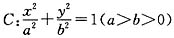
,F为其左焦点,离心率为e.若抛物线y
2=8x的准线经过F点,椭圆C经过点P(2,3),求此椭圆的方程.
解:抛物线y
2=8x的准线为x=-2,所以F(-2,0),椭圆焦点与原点的距离c=2.所以4=a
2-b
2①,又因为椭圆C经过点P(2,3),所以

,结合①和②可得a
2=16,b
2=12,椭圆方程为
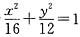
.
四、解答题1. 从4名男生和2名女生中任选3人参加演讲比赛,求所选的3人中至少有1名女生的概率.
2. 设函数f(x)=-x(x-a)
2(x∈R),其中a∈R.
(1)当a=1时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)当a≠0时,求函数f(x)的极大值和极小值,
(1)当a=1时,f(x)=-x(x-1)
2=-x
3+2x
2-x,
f(2)=-2,f′(x)=-3x
2+4x-1,
f′(2)=-12+8-1=-5,
∴当a=1时,曲线y=f(x)在点(2,f(2))处的切线方程为5x+y-8=0.
(2)f(x)=-x(x-a)
2=-x
3+2ax
2-a
2x,
f′(x)=-3x
2+4ax-a
2=-(3x-a)(x-a),
令f′(x)=0,解得
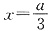
或x=a.
由于a≠0,以下分两种情况讨论,
①若a>0,当x变化时,f′(x)的正负如下表:
因此,函数f(x)在
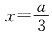
处取得极小值
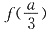
,且
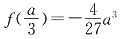
,
函数f(x)在x=a处取得极大值f(a),且f(a)=0.
②若a<0,当x变化时,f′(x)的正负如下表:
因此,函数f(x)在x=a处取得极小值f(a),且f(a)=0;
函数f(x)在
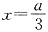
处取得极大值
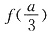
,
且
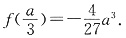
3. 已知向量m=(sinA,cosA),n=(1,-2),且m·n=0。
(1)求tanA的值;
(2)求函数f(x)=cos2x+tanAsinx(x∈R)的值域。
由题意得m·n=sinA-2cosA=0。
∵cosA≠0.
∴tanA=2。
(2)由(1)知tanA=2,
所以

∵x∈R.
∴sinx∈[-1,1]。

当sinx=-1时,f(x)有最小值-3,
所以函数f(x)的值域是

4. 已知:数列{a
n}满足
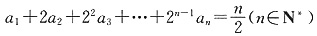
(1)求数列{a
n}的通项;
(2)若
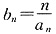
,求数列{b
n}的前n项的和S
n.
(1)n=1时,

,n≥2时,
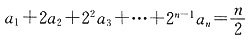
①
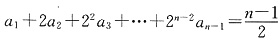
②
①-②得
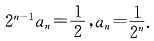
又
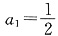
适合上式.
∴
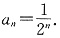
(2)b
n=n·2
n.
S
n=1·2+2·2
2+3·2
3+…+n·2
n.
2S
n=1·2
2+2·2
3+…+(n-1)·2
n+n·2n+1.
∴(1-2)S
n=2+2
2+…+2
n-n·2
n+1 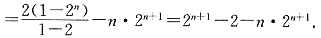
∴S
n=(n-1)2
n+1+2.
 描述学习某学科知识的掌握程度.
描述学习某学科知识的掌握程度.
其中x表示某学科知识的学习次数(x∈N+),f(x)表示对该学科知识的掌握程度,正实数a与学科知识有关.5. 证明:当x≥7时,掌握程度的增加量f(x+1)-f(x)总是下降;
当x≥7时,

.
而当x≥7时,函数y=(x-3)(x-4)单调递增,且(x-3)(x-4)>0.
故f(x+1)-f(x)单调递减.
∴当x≥7,掌握程度的增长量f(x+1)-f(x)总是下降.
6. 根据经验,学科甲、乙、丙对应的a的取值区间分别为(115,121],(121,127],(127,133].
当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
由题意可知

.
整理得

,
解得

由此可知,该学科是乙学科。

 .故选A.
.故选A. 的图像向右平移
的图像向右平移 个单位长度后,与函数
个单位长度后,与函数 的图像重合,则ω的最小值为( ).
的图像重合,则ω的最小值为( ).
 向右平移
向右平移 得
得 ,与函数
,与函数 重合.由上可知:
重合.由上可知: ,所以
,所以 ,假设ω>0,则ω的最小值为
,假设ω>0,则ω的最小值为 .故选D.
.故选D. 种方法,第二步安排剩余两人从乙、丙中各选1门课程有
种方法,第二步安排剩余两人从乙、丙中各选1门课程有 种选法,根据分步计数原理,有6×2=12种选法,故选A。
种选法,根据分步计数原理,有6×2=12种选法,故选A。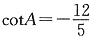 ,则cosA=______.
,则cosA=______.
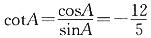 ,cos2A+sin2A=1,由上可得
,cos2A+sin2A=1,由上可得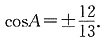 因为在三角形中角大于90°小于180°时,cos为负数,
因为在三角形中角大于90°小于180°时,cos为负数,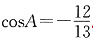 .故选D.
.故选D. 种方法,第二步安排剩余两人从乙、丙中各选1门课程有
种方法,第二步安排剩余两人从乙、丙中各选1门课程有 种选法,根据分步计数原理,有6×2=12种选法,故选A。
种选法,根据分步计数原理,有6×2=12种选法,故选A。 ,则球O的表面积等于______.
,则球O的表面积等于______.



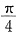 的直线,与抛物线y2=2x交于M、N两点,则|MN|______.
的直线,与抛物线y2=2x交于M、N两点,则|MN|______.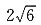
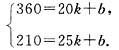
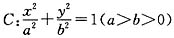 ,F为其左焦点,离心率为e.若抛物线y2=8x的准线经过F点,椭圆C经过点P(2,3),求此椭圆的方程.
,F为其左焦点,离心率为e.若抛物线y2=8x的准线经过F点,椭圆C经过点P(2,3),求此椭圆的方程. ,结合①和②可得a2=16,b2=12,椭圆方程为
,结合①和②可得a2=16,b2=12,椭圆方程为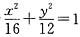 .
.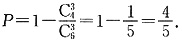
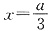 或x=a.
或x=a.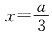 处取得极小值
处取得极小值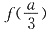 ,且
,且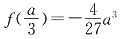 ,
,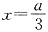 处取得极大值
处取得极大值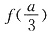 ,
,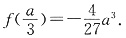



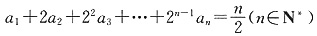
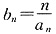 ,求数列{bn}的前n项的和Sn.
,求数列{bn}的前n项的和Sn. ,n≥2时,
,n≥2时,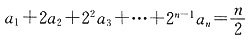 ①
①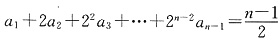 ②
②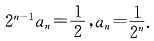
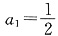 适合上式.
适合上式.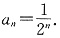
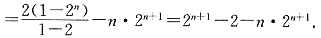
 描述学习某学科知识的掌握程度.
描述学习某学科知识的掌握程度. .
. .
. ,
,
