二、填空题2. 个体从生命开始到结束的全部人生过程中,生理和心理不断向积极方面变化的过程,称之为______.
3. 学生是数学学习的主人,教师是数学学习的组织者、______与______.
4. 数与代数内容主要包括______、______、______、______、______.
6. 义务教育,也叫______,是由国家用立法形式确定下来强制实行的国民基础教育.
7. 中学阶段是理想、动机和兴趣形成与发展的重要阶段,是世界观从萌芽到形成的重要阶段,是______和行为选择的重要阶段.
8. 选择公理的时候,应注意______、______、______的要求.
9. 我国中小学的教学内容,具体体现在中小学各类______和各科课程标准、教科书之中.
10. 在教学史上先后出现的影响较大的教学组织形式有:______、______、分组教学和道尔顿制等.
三、简答题1. 《全日制义务教育数学课程标准(实验稿)》中统计与概率领域的内容及要求有哪具体变化?
(1)反映数据统计的全过程:发现并提出问题,收集和整理数据、表示数据、分析数据,作出合理的决策,对结果进行评价、交流与改进。
(2)体会抽样的必要性和随机抽样的重要性,体会用样本估计总体的初步思想。
(3)根据数据作出推理和合理的论证,并初步学会用概率统计语言进行交流。
2. 教师课外辅导应注意的问题是什么?
教师课外辅导学生要注意以下几点:
(1)从实际出发,因材施教.教师要在全面了解学生的基础上,确定辅导的内容、重点,并根据不同学生的特点采取相应的措施.
(2)目的明确,着重启发.每次辅导要有计划,要充分调动学生的积极性和主动性,引导他们自己寻找解决疑难的门径.
(3)组织学生互相帮助.对差生的辅导可适当组织优秀学生对他们进行帮助,以互相促进、共同提高.但不宜占用优秀学生过多的课外时间.
(4)善于总结、积累经验,辅导时教师要对学生的疑难、存在的问题、个人的体会等做好记录,既可使讲课有的放矢,又可积累资料、掌握规律,有预见性地搞好今后的教学工作.
一、选择题3. 已知向量a=(2,1),a·b=10,

,则|b|=______.
A.
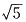
B.
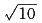
C.5 D.25
A B C D
C
[解析] 由a=(2,1)得:a
2=2
2+1
2=5,由
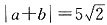
得:a
2+2ab+|b|
2=50,所以|b|
2=25,解得|b|=5. 故选C.
4. 已知等差数列{a
n}前17项和S
17=51,则a
5-a
7+a
9-a
11+a
13=______.
A B C D
A
[解析] S17=a1+…+a17=(2a1+16d)×8+(a1+8d)=(a1+8d)×17=51,a1+8d=3,即a9=3.数列为等差数列,则:a5-a7+a9-a11+a13=a9+(a5+a13)-(a7+a11)=a9=3.故选A.
5. 已知△ABC中,

,则cosA=
.

A B C D
D
[解析]

,cos
2A+sin
2A=1,由上可得

.因为在三角形中角大于90°小于180°时,cos为负数,

.故选D.
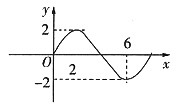
二、填空题1. 函数
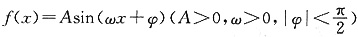
的部分图像如图所示,则f(x) ______.
2.

4. 表面积为4π的球O与平面角为钝角的二面角的两个半平面相切于A、B两点,三角形OAB的面积
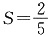
,则球心到二面角的棱的距离为______.
5. 在平面直角坐标系xOy内,曲线y=x
3-3x
2+1在点(1,-1)处的切线方程为______.
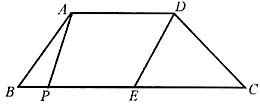
6. 如下图,在梯形ABCD中,AD∥BC,E是BC的中点,AD=5,BC=12,CD=
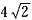
,∠C=45°,点P是BC边上一动点,设PB的长为x.
(1)当x的值为______时,以点P、A、D、E为顶点的四边形为直角梯形;
(2)当x的值为______时,以点P、A、D、E为顶点的四边形为平行四边形.
三、计算题1. 已知复数z
1满足(1+i)z
1=-1+5i,z
2=a-2-i,其中i为虚数单位,a∈R,若
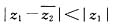
,求a的取值范围.
解:由题意得

,
于是
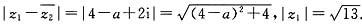
.
由
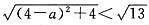
,得a
2-8a+7<0,1<a<7.
2. 某商场购进一批单价为16元的日用品,经试验发现,若按每件20元的价格销售时,每月能卖360件,若按每件25元的价格销售时,每月能卖210件,假定每月销售件数y
(件)是价格x(元/件)的一次函数.
(1)试求y与x之间的关系式;
(2)在商品不积压,且不考虑其他因素的条件下,问销售价格定为多少时,才能使每月获得最大利润?每月的最大利润是多少?
依题意设y=kx+b,则有
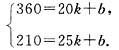
解得是k=30,b=960.
∴y=-30x+960(16≤x≤32).
(2)每月获得利润P=(-30x+960)(x-16)=30(-x
2+48x-512)=-30(x-24)
2+1920.
∴当x=24时,P有最大值,最大值为1920.即当价格为24元,每月才能获得最大利润1920元.
四、解答题1. 从4名男生和2名女生中任选3人参加演讲比赛,求所选的3人中至少有1名女生的概率.
2. 某投资公司计划投资A,B两种金融产品,根据市场调查与预测,A产品的利润与投资量成正比例,其关系如图(1),B产品的利润与投资量的算术平方根成正比例,其关系如图(2)(注:利润与投资量单位:万元)。
(1)分别将A,B两产品的利润表示为投资量的函数关系式;
(2)该公司已有10万元资金,并全部投入A,B两种产品中,问:怎样分配这10万元投资,才能使公司获得最大利润?其最大利润为多少万元?

(1)设投资为x万元,A产品的利润为f(x)万元,B产品的利润为g(x)万元。

(2)设A产品投入x万元,B产品投入(10-x)万元,
设企业利润为y万元,

当A产品投入6万元,B产品投入4万元时,该企业获得最大利润,利润为2.8万元。
3. 某投资公司计划投资A,B两种金融产品,根据市场调查与预测,A产品的利润与投资量成正比例,其关系如图(1),B产品的利润与投资量的算术平方根成正比例,其关系如图(2)(注:利润与投资量单位:万元)。
(1)分别将A,B两产品的利润表示为投资量的函数关系式;
(2)该公司已有10万元资金,并全部投入A,B两种产品中,问:怎样分配这10万元投资,才能使公司获得最大利润?其最大利润为多少万元?

(1)设投资为x万元,A产品的利润为f(x)万元,B产品的利润为g(x)万元。

(2)设A产品投入x万元,B产品投入(10-x)万元,
设企业利润为y万元,

当A产品投入6万元,B产品投入4万元时,该企业获得最大利润,利润为2.8万元。
4. 各项均为正数的数列{a
n}的前n项和S
n,函数
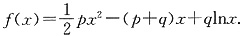
(其中p、q均为常数,且p>q>0),当x=a
1时,函数f(x)取得极小值,点(a
n,2S
n)(n∈N
*)均在函数
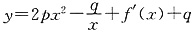
的图像上,(其中f′(x)是函数f(x)的导函数).
(1)求a
1的值;
(2)求数列{a
n}的通项公式;
(3)记
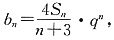
求数列{b
n}的前n项和T
n.
(1)
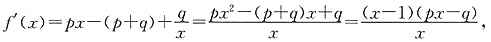
令f′(x)=0,得x=1或
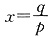
,∵
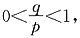
当x的值变化时,f′(x),f(x)的变化情况如下表:

所以f(x)在x=1处取得最小值,即a
1=1.
(2)因为
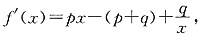
所以
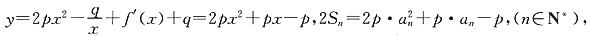
由于a
1=1,所以
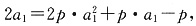
得p=1.
∴
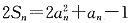
①
又∴
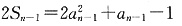
②
①-②得
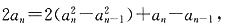
∴
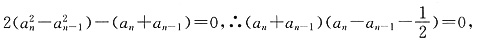
由于a
n+a
n-1>0,∴
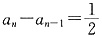
,所以{a
n}是以a
1=1,公差为
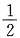
的等差数列,
∴

(3)
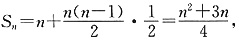
由
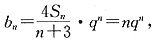
所以,T
n=q+2q
2+3q
3+…+(n-1)q
n-1+nq
n,由p>q>0,而p=1,故q≠1,
qT
n=q
2+2q
3+3q
4+…+(n-1)q
n+nq
n+1,
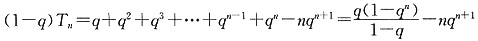
∴
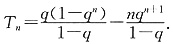
5. 已知可行域
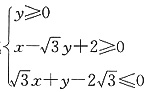
的外接圆C与x轴交于点A
1、A
2,椭圆C
1以线段A
1A
2为长轴,离心率
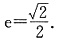
(1)求圆C及椭圆C
1的方程;
(2)设椭圆C
1的右焦点为F,点P为圆C上异于A
1、A
2的动点,过原点O作直线PF的垂线交直线
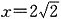
于点Q,判断直线PQ与圆C的位置关系,并给出证明.
(1)由题意可知,可行域是以A
1(-2,0),A
2(2,0)及点
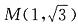
为顶点的三角形,
∵A
1M⊥A
2M,∴△A
1A
2M为直角三角形,
∴外接圆C以原点O为圆心,线段A
1A
2为直径,故其方程为x
2+y
2=4.
∵2a=4,∴a=2.又
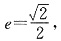
∴
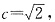
可得
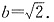
∴所求椭圆C
1的方程是
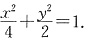
(2)直线PQ与圆C相切.设P(x
0,y
0)(x
0≠±2),则
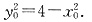
当
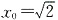
时,
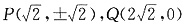
,k
PQ=-1,∴OP⊥PQ;
当
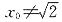
时,
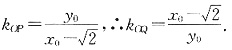
∴直线OQ的方程为
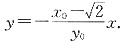
点Q的坐标为
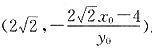
,
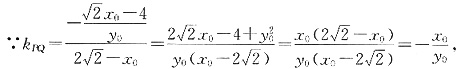
∴当x
0=0时,k
PQ=0,OP⊥PQ;
当x
0≠0时,
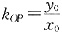
,∴k
PQ·k
OP=-1,OP⊥PQ.
综上,当x
0≠±2时,OP⊥PQ,故直线PQ始终与圆C相切.
6. 如图,一船在海上由西向东航行,在A处测得某岛M的方位角为北偏东α角,前进4km后在B处测得该岛的方位角为北偏东β角,已知该岛周围3.5km范围内有暗礁,现该船继续东行.
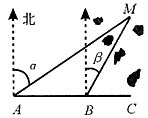
(1)若α=2β=60°,问该船有无触礁危险?如果没有,请说明理由;如果有,那么该船自B处向东航行多少距离会有触礁危险?
(2)当α与β满足什么条件时,该船没有触礁危险?
解:(1)作MC⊥AB,垂足为C,由已知α=60°,β=30°,所以∠ABM=120°,∠AMB=30°.
所以BM=AB=4,∠MBC=60°,所以
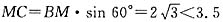
,
所以该船有触礁的危险.
设该船自B向东航行至点D有触礁危险,
则MD=3.5,在△MBC中,BM=4,BC=2,
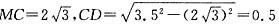
,所以,BD=1.5(km).
所以,该船自西向东航行1.5km会有触礁危险.
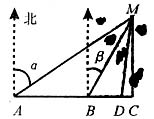
(2)设CM=x,在△MAB中,由正弦定理得,
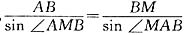
,即
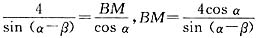
,
而
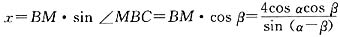
,
所以,当x>3.即
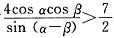
,
即
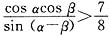
时,该船没有触礁危险.
 ,则|b|=______.
,则|b|=______.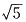 B.
B.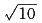
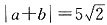 得:a2+2ab+|b|2=50,所以|b|2=25,解得|b|=5. 故选C.
得:a2+2ab+|b|2=50,所以|b|2=25,解得|b|=5. 故选C. ,则cosA= .
,则cosA= .
 ,cos2A+sin2A=1,由上可得
,cos2A+sin2A=1,由上可得 .因为在三角形中角大于90°小于180°时,cos为负数,
.因为在三角形中角大于90°小于180°时,cos为负数, .故选D.
.故选D.
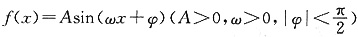 的部分图像如图所示,则f(x) ______.
的部分图像如图所示,则f(x) ______.
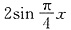


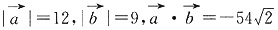 ;则
;则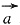 和
和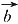 的夹角θ为______.
的夹角θ为______.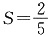 ,则球心到二面角的棱的距离为______.
,则球心到二面角的棱的距离为______.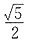
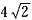 ,∠C=45°,点P是BC边上一动点,设PB的长为x.
,∠C=45°,点P是BC边上一动点,设PB的长为x.
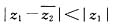 ,求a的取值范围.
,求a的取值范围. ,
,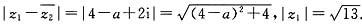 .
.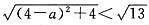 ,得a2-8a+7<0,1<a<7.
,得a2-8a+7<0,1<a<7.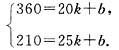
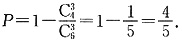






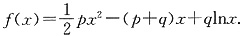 (其中p、q均为常数,且p>q>0),当x=a1时,函数f(x)取得极小值,点(an,2Sn)(n∈N*)均在函数
(其中p、q均为常数,且p>q>0),当x=a1时,函数f(x)取得极小值,点(an,2Sn)(n∈N*)均在函数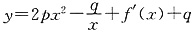 的图像上,(其中f′(x)是函数f(x)的导函数).
的图像上,(其中f′(x)是函数f(x)的导函数).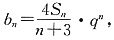 求数列{bn}的前n项和Tn.
求数列{bn}的前n项和Tn.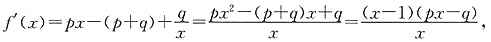
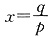 ,∵
,∵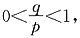

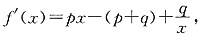
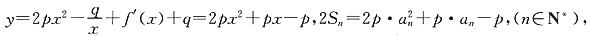
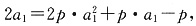 得p=1.
得p=1.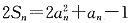 ①
①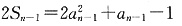 ②
②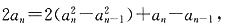
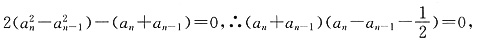
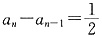 ,所以{an}是以a1=1,公差为
,所以{an}是以a1=1,公差为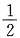 的等差数列,
的等差数列,
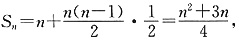 由
由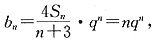
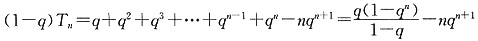
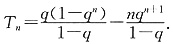
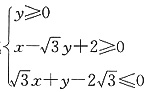 的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率
的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率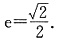
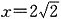 于点Q,判断直线PQ与圆C的位置关系,并给出证明.
于点Q,判断直线PQ与圆C的位置关系,并给出证明.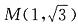 为顶点的三角形,
为顶点的三角形,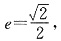 ∴
∴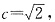 可得
可得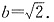
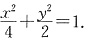
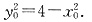
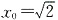 时,
时,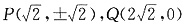 ,kPQ=-1,∴OP⊥PQ;
,kPQ=-1,∴OP⊥PQ;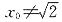 时,
时,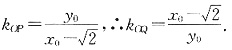
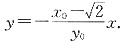 点Q的坐标为
点Q的坐标为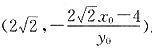 ,
,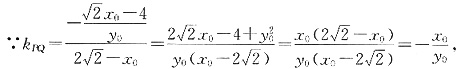
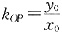 ,∴kPQ·kOP=-1,OP⊥PQ.
,∴kPQ·kOP=-1,OP⊥PQ.
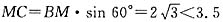 ,
,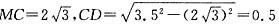 ,所以,BD=1.5(km).
,所以,BD=1.5(km).
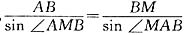 ,即
,即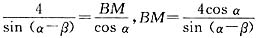 ,
,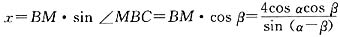 ,
,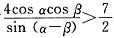 ,
,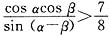 时,该船没有触礁危险.
时,该船没有触礁危险.