一、单项选择题 2. 数列{a
n }满足a
n+1 =a
n -3(n≥1)且a
1 =7,则a
3 的值是______.
A
[解析] 由题意得,a3 =a1 -3-3=1.故选A.
二、填空题 1. 已知z∈C,|z-2|=1,则|z+2+3i|的最大值和最小值分别是______。
2. 某小朋友用手指按如图所示的规则练习数数,数到2009时对应的指头是______。(填出指头名称:各指头对应依次为大拇指、食指、中指、无名指、小拇指)
3. 过点A(2,-3),B(-2,-5),圆心在直线x-2y-3=0上的圆的方程是______.
4. 将参加数学竞赛的1000名学生编号如下:0001,0002,0003……1000,打算从中抽取一个容量为50的样本,按系统抽样的办法分成50个部分.如果第一部分编号为0001,0002……0020,从中随机抽取一个号码为0015,则第40个号码为______.
5. 在一个不透明的布袋中装有2个白球和n个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球,摸到黄球的概率是
,则n=______.
8
袋中有2个白球和n个黄球,从中随机摸一个黄球的概率为
,解得n=8.
三、计算题 1. 已知数列{a
n }中,S
n 是它的前n项和,并且S
n+1 =4a
n +2,a
1 =1.
(1)设b
n =a
n+1 -2a
n ,求证{b
n }是等比数列;
(2)设
求证{C
n }是等差数列;
(3)求数列{a
n }的通项公式及前n项和公式.
(1)S
n+1 =S
n +a
n+1 =4a
n-1 +2+a
n+1 ∴4a
n +2=4a
n-1 +2+a
n+1 ∴a
n+1 -2a
n =2(a
n -2a
n-1 )
即:
且b
1 =a
2 -2a
1 =3
∴{b
n }是等比数列
(2){b
n }的通项b
n =b
1 ·q
n-1 =3·2
n-1 ∴
又
∴{C
n }为等差数列
(3)∵
∴
∴a
n =(3n-1)·2
n-2 (n∈N
* )
S
n+1 =4·a
n +2=4·(3n-1)·2
n-2 +2=(3n-1)·2
n +2
∴S
n =(3n-4)2
n-1 +2(n∈N
* )
2. 设f(x)是一个多项式,对所有实数x有f(x[
2 ]+1)=x[
4 ]+5x[
2 ]+3.求f(x[
2 ]-1).
令x2 +1=t,则x2 =t-1.2 +1)=x4 +5x2 +3,得:2 +5(t-1)+3=t2 +3t-1.2 -1)+3(x2 -1)-1=x4 +x2 -3.
3. 已知可行域
的外接圆C与x轴交于点A
1 、A
2 ,椭圆C
1 以线段A
1 A
2 为长轴,离心率
(1)求圆C及椭圆C
1 的方程;
(2)设椭圆C
1 的右焦点为F,点P为圆C上异于A
1 、A
2 的动点,过原点O作直线PF的垂线交直线
于点Q,判断直线PQ与圆C的位置关系,并给出证明,
(1)由题意可知,可行域是以A
1 (-2,0)、A
2 (2,0)及点
为顶点的三角形,
∵A
1 M⊥A
2 M,∴△A
1 A
2 M为直角三角形,
∴外接圆C以原点O为圆心,线段A
1 A
2 为直径,故其方程为x
2 +y
2 =4
∵2a=4,∴a=2.又
,∴
,可得
∴所求椭圆C
1 的方程是
(2)椭圆C
1 的右焦点为
设点P的坐标为(m,n),(n≠0,m≠2,-2).
①当直线PF斜率不存在时,P点坐标为
或
∴过原点O作直线PF的垂线交直线
于点Q,点Q坐标为
则k(PQ)=-1或1,PQ方程为:
或
则圆心(0,0)到PQ直线的距离都为d=2=r
∴直线PQ与圆C相切
②当直线PF斜率存在时,则
过原点O作直线PF的垂线斜率为:
∴过原点O作直线PF的垂线方程为:
联立方程:
①,
②
解得:
∴点Q的坐标为
又点P(m,n)在圆上,∴n
2 -4=m
2 又直线OP的斜率为:
∵P为圆的半径的端点且PQ⊥OP
∴直线PQ与圆C的相切
综上所述:直线PQ与圆C相切.
4. 设
(1)若f(x)在
上存在单调递增区间,求a的取值范围;
(2)当0<a<2时,f(x)在[1,4]上的最小值为
求f(x)在该区间上的最大值.
(1)f(x)在
上存在单调递增区间,即存在某个子区间
+∞)使得f′(x)>0.由
,f′(x)在区间
∞)上存在单调递增区间,则只需
即可,由
解得
所以,当
时,f(x)在
上存在单调递增区间.
(2)令f′(x)=0,得两根
所以f(x)在(-∞,x
1 ),(x
2 ,+∞)上单调递减,在(x
1 ,x
2 )上单调递增
当0<a<2时,有x
1 <1<x
2 <4,所以f(x)在[1,4]上的最大值为f(x
2 )
又
,即f(4)<f(1)
所以f(x)在[1,4]上的最小值为
得a=1,x
2 =2,
从而f(x)在[1,4]上的最大值为
5. 如图,在直三棱柱ABC-A
1 B
1 C
1 中,∠BAC=90°,AB=AC=AA
1 =1,延长A
1 C
1 至点P,使C
1 P=A
1 C
1 ,连接AP交棱CC
1 于D。
(1)求证:PB
1 ∥平面BDA
1 ;
(2)求二面角A-A
1 D-B的平面角的余弦值。
[解法一] (1)连结AB
1 与BA
1 交于点O,连结OD,
∵C
1 D∥AA
1 ,A
1 C
1 =C
1 P∴AD=PD,又AO=B
1 O,
∴OD∥PB
1 ,又OD
面BDA
1 ,PB
1 面BDA
1 ,
∴PB
1 ∥平面BDA
1 (2)过A作AE⊥DA
1 于点E,连结BE∵BA⊥CA,BA⊥AA
1 ,且
AA
1 ∩AC=A,
∴BA⊥平面AA
1 C
1 C。
由三垂线定理可知BE⊥DA
1 ,
∴∠BEA为二面角A-A
1 D-B的平面角。
在Rt△A
1 C
1 D中,
故二面角A-A
1 D-B的平面角的余弦值为
。
[解法二]
如图,以A
1 为原点,A
1 B
1 ,A
1 C
1 ,A
1 A所在直线分别为x轴,y轴,z轴建立空间直角坐标系A
1 -B
1 C
1 A,则A
1 (0,0,0),B
1 (1,0,0),C
1 (0,1,0),B(1,0,1),P(0,2,0).
(1)在△PAA
1 中有
即
设平面BA
1 D的一个法向量为n
1 =(a,b,c),
∴PB
1 ∥平面BA
1 D。
(2)由(1)知,平面BA
1 D的一个法向量
又n
2 =(1,0,0)为平面AA1
D的一个法向量,∴
故二面角A-A
1 D-B的平面角的余弦值为
四、应用题 1. 列方程或方程组解应用题:
北京市实施交通管理新措施以来,全市公共交通客运量显著增加.据统计,2008年10月11日至2009年2月28日期间,地面公交日均客运量与轨道交通日均客运量总和为1696万人次,地面公交日均客运量比轨道交通日均客运量的4倍少69万人次.在此期间,地面公交和轨道交通日均客运量分别为多少万人次?
设轨道交通日均客运量为x万人次,则地面公交日均客运量为(4x-69)万人次.
2. 如下图所示,桌面上放置了红、黄、蓝三个不同颜色的杯子,杯口朝上,我们做蒙眼睛翻杯子(杯口朝上的翻为杯口朝下,杯口朝下的翻为杯口朝上)的游戏.
(1)随机翻一个杯子,求翻到黄色杯子的概率;
(2)随机翻一个杯子,接着从这三个杯子中再随机翻一个,请利用树状图求出此时恰好有一杯口朝上的概率.
(2)将杯口朝上用“上”表示,杯口朝下用“下”表示,画树状图如下:
由上面树状图可知:所有等可能出现的结果共有9种,其中恰好有一个杯口朝上的有6种,
3. 如下图所示,左边的楼高AB=60m,右边的楼高CD=24m,且BC=30m,地面上的目标
P位于距点C 15m处.
(1)请画出从A处看地面上距离点C最近的点.这个点与点C之间的距离是多少?
(2)从A处能看见目标P吗?为什么?
(1)如图,连接AD交BC的延长线于M,则M点即为所求的点.
∴这个点与点C之间的距离是20m.
(2)∵20>15,∴从A处不能看见目标P.
五、证明题 1. 如图,在△ABC中,∠A所对的BC边的边长等于m,旁切圆⊙O的半径为R,且分别切BC及AB、AC的延长线于D,E,F.求证:
作△ABC的内切圆O',分别切三边于G,H,K.由对称性知GE=KF(如右图).设GB=a,BE=x,KC=y,CF=b.
则x+a=y+b, ①
且BH=a,BD=x,HC=y,DC=b.于是,
x-a=y-b. ②
①+②得,x=y.从而知a=b.
∴GE=BC=m.
设⊙O'半径为r.显然R+r≤OO'(当AB=AC时取等号).
2. 以直角三角形ABC的两直角边AC、BC为一边各向外侧作正方形ACDE、BCGH,连结BE、AH分别交AC、BC于P、Q.求证:CP=CQ.
如图,连接HE,GQ,PD,显然S
△GCQ =S
△HCQ ,
∵HB∥AG,
∴S
△ACH =S
△ABC .
S
△ACH =S
△HCQ +S
△ACQ =S
△GCQ +S
△ACQ =S
△ACQ .
∴S
△ACQ =S
△ABC ,
同理,S
△PCD =S
△PCE ,S
△BCE =S
△ABC ,
∴S
△BDP =S
△BCP +S
△PCD =S
△BCP +S
△PCE =S
△BCE .
∴S
△BDP =S
△ABC .
∴S
△AGQ =S
△BDP ,
∴CQ·AG=CP·BD.
∵AG=AC+GC
=DC+BC=BD。
∴CP=CQ.

 的解是负数,则a的取值范围是 .
的解是负数,则a的取值范围是 . ,得x=a-1,∵方程的解是负数,∴a-1<0,∴a<1,又∵x+1≠0,∴a-1+1≠0,∴a≠0,∴a<1且a≠0,故选B.
,得x=a-1,∵方程的解是负数,∴a-1<0,∴a<1,又∵x+1≠0,∴a-1+1≠0,∴a≠0,∴a<1且a≠0,故选B. 的图象与x轴所围成的封闭图形的面积为 。
的图象与x轴所围成的封闭图形的面积为 。


 所以x+2=0且y-2=0,∴x=-2,y=2.
所以x+2=0且y-2=0,∴x=-2,y=2. 故选B.
故选B.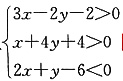 的整数解的个数为______.
的整数解的个数为______. 展开式中,各项系数的和为64,则n等于( )。
展开式中,各项系数的和为64,则n等于( )。

 ,则n=______.
,则n=______. ,解得n=8.
,解得n=8.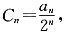 求证{Cn}是等差数列;
求证{Cn}是等差数列;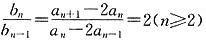 且b1=a2-2a1=3
且b1=a2-2a1=3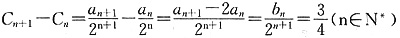
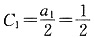 ∴{Cn}为等差数列
∴{Cn}为等差数列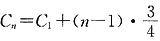 ∴
∴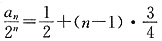
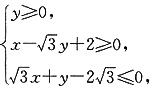 的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率
的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率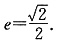
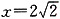 于点Q,判断直线PQ与圆C的位置关系,并给出证明,
于点Q,判断直线PQ与圆C的位置关系,并给出证明,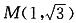 为顶点的三角形,
为顶点的三角形,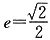 ,∴
,∴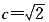 ,可得
,可得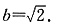
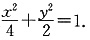
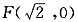 设点P的坐标为(m,n),(n≠0,m≠2,-2).
设点P的坐标为(m,n),(n≠0,m≠2,-2).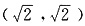 或
或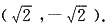
 于点Q,点Q坐标为
于点Q,点Q坐标为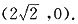
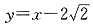 或
或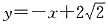
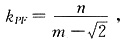 过原点O作直线PF的垂线斜率为:
过原点O作直线PF的垂线斜率为: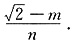
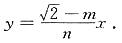
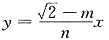 ①,
①,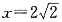 ②
②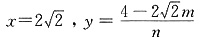
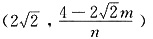
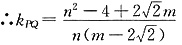
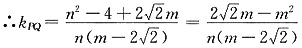
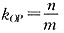
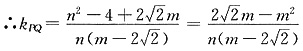
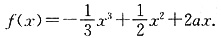
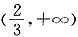 上存在单调递增区间,求a的取值范围;
上存在单调递增区间,求a的取值范围;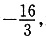 求f(x)在该区间上的最大值.
求f(x)在该区间上的最大值.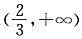 上存在单调递增区间,即存在某个子区间
上存在单调递增区间,即存在某个子区间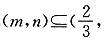 +∞)使得f′(x)>0.由
+∞)使得f′(x)>0.由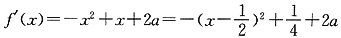 ,f′(x)在区间
,f′(x)在区间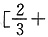 ∞)上存在单调递增区间,则只需
∞)上存在单调递增区间,则只需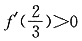 即可,由
即可,由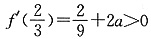 解得
解得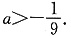
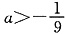 时,f(x)在
时,f(x)在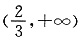 上存在单调递增区间.
上存在单调递增区间.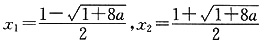
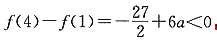 ,即f(4)<f(1)
,即f(4)<f(1)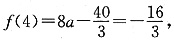 得a=1,x2=2,
得a=1,x2=2,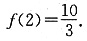


 面BDA1,PB1
面BDA1,PB1 面BDA1,
面BDA1,

 。
。
 即
即



















