一、单项选择题1. 设坐标原点为O,抛物线y
2=2x与过焦点的直线交于A、B两点,则
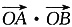
的值是______.
A.-3 B.-1
C.
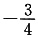
D.
A B C D
C
[解析] 抛物线y
2=2x的焦点为
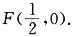
设过F的直线方程为
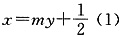
代入y
2=2x化简得
y
2-2my-1=0,
设A(x
1,y
1),B(x
2,y
2),则
y
1+y
2=2m,y
1y
2=-1.
由(1)

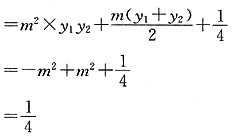
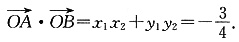
故选C.
3. 已知Ι为全集,P、Q为非空集合,且
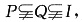
则下列结论不正确的是______.

A B C D
C
[解析] 由P、Q为非空集合,且
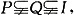
可以作图如下:
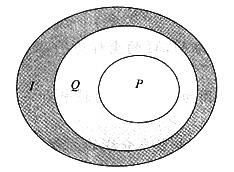
C选项中:集合P是集合P在集合Ι中的补集,作图如下:
由上图可知:
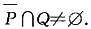
故选C.
二、填空题1. 如果实数x、y满足不等式组

,贝x
2+y
2的最小值是______。
2. 不等式
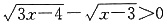
的解集是______.
3. 计算

的值是______。
4. 已知z∈C,|z-2|=1,则|z+2+3i|的最大值和最小值分别是______.
5. 如下图所示,若AB∥CD,EF与AB、CD分别交于点E、F,EP⊥EF,∠EFD的平分线与EP相交于点P,且∠BEP=40°,则∠EPF=______度.

65°
因为EP⊥EF,所以∠PEF=90°,又根据两直线平行,同旁内角互补,∠EFD=180°-∠FEB=180°-(90°+40°)=50°,FP平分∠EFD,所以∠EFP=

∠EFD=25°,在Rt△FEP中,∠EPF=90°-∠EFP=65°.
四、应用题1. 本电视机生产厂家去年销往农村的某品牌电视机每台的售价y(元)与月份x之间满足函数关系y=-50x+2600,去年的月销售量p(万台)与月份x之间成一次函数关系,其中每个月的销售情况如下表:
(1)求该品牌电视机在去年哪个月销往农村的销量金额最大?最大是多少?
(2)由于受国际金融危机的影响,今年1、2月份该品牌电视机销往农村的售价都比去年12月份下降了m%,且每月的销售量都比去年12月份下降了1.5m%.国家实施“家电下乡”政策,即对农村家庭购买新的家电产品,国家按该产品售价的13%给予了财政补贴.受此政策的影响,今年3至5月份,该厂家销售到农村的这种电视机在保持今年2月份的售价不变的情况下,平均每月的销售量比今年2月份增加了1.5万台.若今年3至5月份国家对这种电视机的销售共给予了财政补贴936万元,求m的值(保留一位小数).

(1)设p与x的函数关系为P=kx+b(k≠0),根据题意,得:

设月销售金额为ω万元,则
ω=py=(0.1x+31.8)(-50x+2600),
化简,得ω=-5x
2+70x+9880,
所以,ω=-5(x-7)
2+10125.
当x=7时,叫取得最大值,最大值为10125.
答:该品牌电视机在去年7月份销往农村的销售金额最大,最大是10125万元.
(2)去年12月份每台的售价为-50×12+2600=2000(元),
去年12月份的销售量为0.1×12+3.8=5(万台),
根据题意,得2000(1-m%)×[5(1-1.5m%)+1.5]×13%×3=936。
令m%=t,原方程可化为7.5t
2-14t+5.3=0.
∴t
1≈0.528,t
2≈1.339(舍去).
答:m的值约为52.8.
2. 一个不透明的口袋里装有红、白、黄三种颜色的乒乓球(除颜色外其余都相同),其中有白球2个,黄球1个,若从中任意摸出一个球,这个球是白球的概率为0.5.
(1)求口袋中红球的个数;
(2)若从中摸出一个球后不放回,再摸出一个球,通过画树状图或列表分析,求两次均摸到白球的概率.
(1)设红球的个数为x

,解得x=1.
经检验:x=1是所列方程根且符合题意.
答:口袋中红球的个数为1个.
(2)用树状图分析如下:

或列表分析:
| |
白球1 |
白球2 |
黄球 |
红球 |
| 白球1
|
|
(白2,白1) |
(黄,白1) |
(红,白1) |
| 白球2 |
(白1,白2) |
|
(黄,白2) |
(红,白2) |
| 黄球 |
(白1,黄) |
(白2,黄) |
|
(红,黄) |
| 红球 |
(白1,红) |
(白2,红), |
(黄,红) |
|
共有12种可能结果,其中2个白球的可能结果是2个.
所以两次均摸到白球的概率为

答:两次均摸到白球的概率为

.
五、证明题1. 已知:如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,DE⊥AC于点F,交BC于点G,交AB的延长线于点E,且AE=AC.
(1)求证:BG=FG;
(2)若AD=DC=2,求AB的长.

(1)在△ABC和△AFE中,

∴△ABC≌△AFE,
∴AB=AF.
又AE=AC,
∴BE=CF.
∴在△EBG和△CFG中,

∴△EBG≌△CFG,
∴BG=FG.
(2)∵AD=DC=2,DE⊥AC,AE=AC,
∴AF=FC。
∴AE=2AF=2AB.
∵∠AFE=∠EAD=90°.∴△EAF∽Λ△EDA.

2. 在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=30°,求∠ACF的度数.

(1)∵∠ABC=90°,
∴∠CBF=∠ABE=90°.
在Rt△ABE和Rt△CBF中有:

∴Rt△ABE≌Rt△CBF(HL).
(2)∵AB=BC,∠ABC=90°,
∴∠CAB=∠ACB=45°.
又∵∠BAE=∠CAB-∠CAE=45°-30°=15°,
由(1)知:Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=15°,
∴∠ACF=∠BCF+∠ACB=45°+15°=60°.
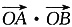 的值是______.
的值是______.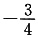 D.
D.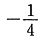
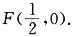
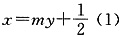

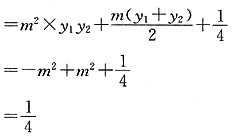
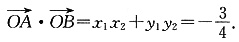 故选C.
故选C.
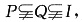 则下列结论不正确的是______.
则下列结论不正确的是______.
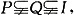 可以作图如下:
可以作图如下:
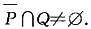 故选C.
故选C.
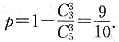 故选D.
故选D. ( )。
( )。 即f(x)=f(-x),所以f(x)为偶函数。
即f(x)=f(-x),所以f(x)为偶函数。 O中,弦AD∥BC,DA=DC,∠AOC=160°,则∠BCO等于 。
O中,弦AD∥BC,DA=DC,∠AOC=160°,则∠BCO等于 。
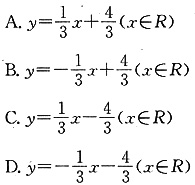
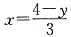 ,即原函数的反函数为
,即原函数的反函数为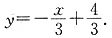 故选B.
故选B. ,贝x2+y2的最小值是______。
,贝x2+y2的最小值是______。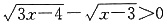 的解集是______.
的解集是______. 的值是______。
的值是______。
 ∠EFD=25°,在Rt△FEP中,∠EPF=90°-∠EFP=65°.
∠EFD=25°,在Rt△FEP中,∠EPF=90°-∠EFP=65°.


 ,
,




 ,0),准线方程
,0),准线方程





 ,解得x=1.
,解得x=1.

 .
.





