一、填空题1. 设f(x)有一阶连续导数,且f(0)=0,f'(0)=1,则
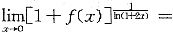
______.
[解析] 当x→0时,
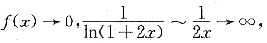
所以该极限为“1
∞”型,所以
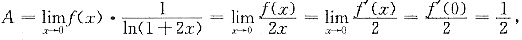
所以原极限
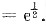
2. 设函数y=y(x)由参数方程
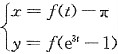
所确定,其中f可导,且f'(0)≠0,则

3
[解析]
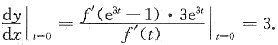
4. 设φ(u,v,w)有一阶连续偏导数,z=z(x,y)是由φ(bz-cy,cx-az,ay-bx)=0确定的函数,则
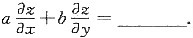
c
[解析] φ(bz-cy,cx-az,ay-bx)=0两边对x求偏导得
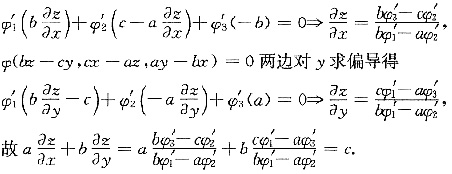
5. 设D为闭区域x
2+y
2≤1,则
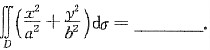
6. 设n阶可逆矩阵A满足
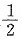
|A|=|kA|,k>0,则k=______.
1
[解析] |A|=|kA|
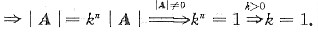
二、选择题1. 设f(x)与g(x)在x=0的某去心邻域内有定义,并且当x→0时,f(x)与g(x)都为x的同阶无穷小,则当x→0时,______
- A.f(x)-g(x)必是x的同阶无穷小.
- B.f(x)-g(x)必是x的高阶无穷小.
- C.f(g(x))必是x的同阶无穷小.
- D.f(g(x))必是x的高阶无穷小.
A B C D
C
[解析] 由题设可知,
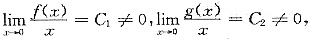
则
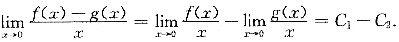
当C
1=C
2时,选项B成立,当C
1≠C
2时,选项A成立.所以可排除A,B选项.
而

所以当x→0时,f(g(x))必是x的同阶无穷小,故选C.
2. 设f(x)在[a,b]上可导,且f'(a)f'(b)<0,则下列命题
①至少存在一点x
0∈(a,b),使得f(x
0)<f(a)
②至少存在一点x
0∈(a,b),使得f(x
0)>f(b)
③至少存在一点x
0∈(a,b),使得f'(x
0)=0
④至少存在一点x
0∈(a,b),使得f(x
0)=
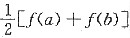
正确的个数为______
A B C D
A
[解析] 因为f'(a)f'(b)<0,不妨设f'(a)<0,f'(b)>0,
则
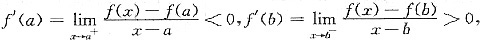
由极限的保号性可得,存在x
1,x
2∈(a,b),使得
f(x
1)-f(a)<0,f(x
2)-f(b)<0,
所以f(a),f(b)不是f(x)在[a,b]上的最小值,所以f(x)在[a,b]上的最小值只可能在(a,b)内取得,由费尔马定理可知,至少存在一点x
0∈(a,b),使得f'(x
0)=0.
其他命题可用举反例排除法来求解.
令f(x)=x-x
2,则f(x)在[0,1]可导,且
f'(0)=1,f'(1)=-1
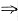
f'(0)f'(1)=-1<0.
但对于x∈(0,1),f(x)=x(1-x)>0=f(0)=f(1),可排除①④;
令f(x)=x
2-x,则f(x)在[0,1]可导,且
f'(0)=-1,f'(1)=1
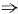
f'(0)f'(1)=-1<0,
但对于x∈(0,1),f(x)=x(x-1)<0=f(0)=f(1),可排除②.
综上,故选A.
4. 已知y=y(x)是(x
2+y
2)dy=dx-dy的任意解,则______

A B C D
C
[解析] 由(x
2+y
2)dy=dx-dy可得
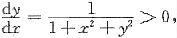
所以y=y(x)在(-∞,+∞)单调增加.
对
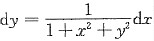
在[x
0,x](x
0<x)两边积分得
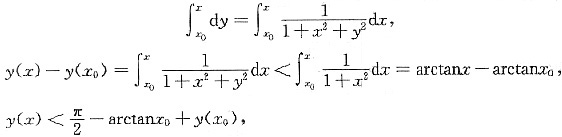
所以y=y(x)在(-∞,+∞)单调增加有上界,即
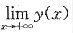
存在.
同理可得
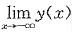
存在,故选C.
5. 设f(t)为连续函数,a是常数,下述命题正确的是______
A.若f(t)是奇函数,则
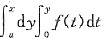
是x的奇函数.
B.若f(t)是偶函数,则
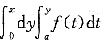
是x的奇函数.
C.若f(t)是奇函数,则
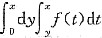
是x的奇函数.
D.若f(t)是偶函数,则

是x的奇函数.
A B C D
C
[解析] 本题可用举反例法来做.
设f(t)=t,则f(t)是奇函数且连续,
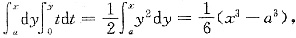
此式是否为奇函数与a有关,排除A.
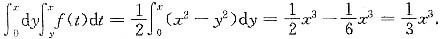
设f(t)=1,则f(t)是偶函数且连续,
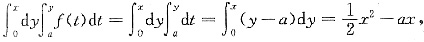
不是奇函数,可排除B.
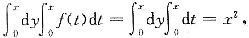
为偶函数,可排除D.
综上,故选C.
6. 设在全平面上有

则在下列条件中使f(x
1,y
1)<f(x
2,y
2)成立的是______
- A.x1<x2,y1<y2.
- B.x1<x2,y1>y2.
- C.x1>x2,y1<y2.
- D.x1>x2,y1>y2.
A B C D
B
[解析] 由
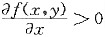
可知,固定y,f(x,y)关于x单调增加;
由
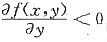
可知,固定x,f(x,y)关于y单调减少.
所以,当x
1<x
2时,有f(x
1,y
1)<f(x
2,y
1);
当y
1>y
2时,有f(x
2,y
1)<f(x
2,y
2).
综上,当x
1<x
2,y
1>y
2时,有f(x
1,y
1)<f(x
2,y
1)<f(x
2,y
2).故选B.
7. 设A为三阶矩阵,E为三阶单位阵,α,β是两个线性无关的三维列向量,且A的行列式|A|=0,Aα=β,Aβ=α,则行列式|A+3E|的值等于______
A B C D
D
[解析] 由|A|=0
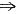
λ=0是A的一个特征值,
又由Aα=β,Aβ=α可得A(α+β)=α+β,A(α-β)=-(α-β),
而α,β线性无关,所以α+β≠0,α-β≠0,所以1,-1是A的另外两个特征值,
因此A的特征值为0,1,-1,于是A+3E的特征值为3,4,2,故|A+3E|=3×4×2=24,
即选D.
三、解答题1. 设f''(x)连续且f''(x)>0,f'(0)=0,求极限
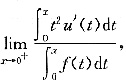
其中u(x)是曲线y=f(x)在x点处的切线在x轴上的截距.
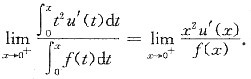
由导数的几何意义,曲线y=f(x)在x点处的切线方程为
Y-f(x)=f'(x)(X-x),
令Y=0,则
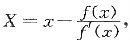
于是
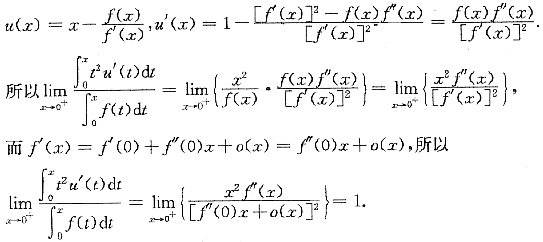
2. 求所有(0,+∞)上的正连续函数g(x),使得对任意x>0有
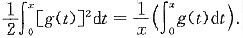
题设等式两边对x求导,并整理得
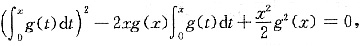
解得
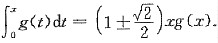
上式两边对x求导得
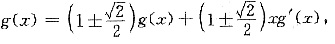
即
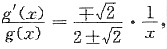
两边积分,
得
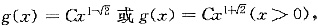
其中C为任意正数.
3. 设|a|≤1,求I(a)=
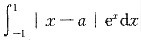
的最大值.
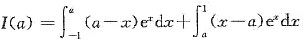
=-a(e+e
-1)+2e
a-2e
-1 令
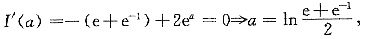
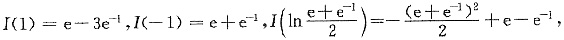
比较后得最大值为I(-1)=e+e
-1.
4. 设f''(x)在[0,1]上连续,且f(0)=f(1)=0,求证:
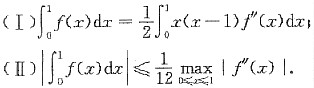
5. 设x
0>0,
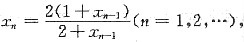
证明
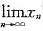
存在,并求之.
对一切n,恒有
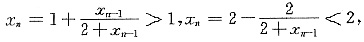
因此数列{x
n}有界.又
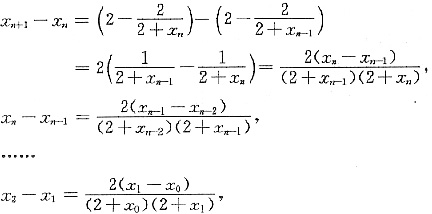
于是可知x
n+1-x
n与x
1-x
0同号,故当x
1>x
0时,x
n+1>x
n,数列{x
n}单调递增;当x
1<x
0时,x
n+1<x
n,数列{x
n}单调递减,即数列{x
n}为单调有界数列,所以
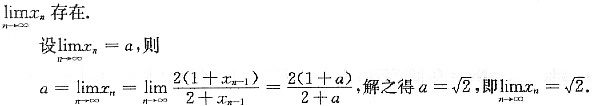
6. 证明方程2
x=x
2+1有且仅有三个实根.
令f(x)=2x-x2-1,显然f(0)=f(1)=0.
又f(2)=-1<0,f(5)=6>0,且f(x)连续,由连续函数的零点定理知f(x)在(2,5)内至少存在一个零点,从而f(x)至少有三个零点.
若f(x)有四个或四个以上的零点,则由罗尔定理知f'''(x)=2xln32至少有一个零点,这是不可能的,故f(x)至多有三个零点.
综上可知f(x)有且仅有三个零点,即方程2x=x2+1有且仅有三个实根.
7. 设D:0≤x≤2,0≤y≤2.
(Ⅰ)求
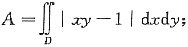
(Ⅱ)设f(x,y)在D上连续,且
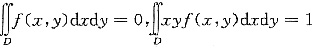
,
证明:存在(ξ,η)∈D,使|f(ξ,η)|≥
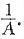
(Ⅰ)令
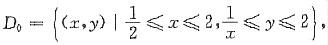
有
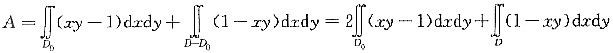
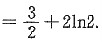
(Ⅱ)因为f(x,y)在D上连续,得|f(x,y)|在D上连续,所以,|f(x,y)|在D上存在最大值,即存在点(ξ,η)∈D,使得|f(ξ,η)|为|f(x,y)|在D上的最大值.由已知得
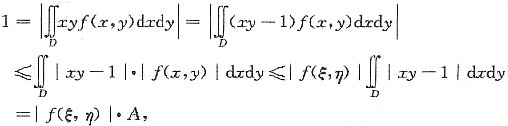
即存在(ξ,η)∈D,使
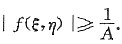
8. 设齐次线性方程组
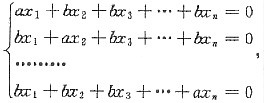
其中a≠0,b≠0,n≥2.试讨论a,b为何值时,方程组仅有零解、有无穷多组解?在有无穷多组解时,求出全部解,并用基础解系表示全部解.
所给方程组的系数矩阵为A,则
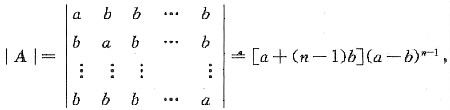
由此可知,
(Ⅰ)当a+(n-1)b≠0且a≠b时,即a≠b且a≠(1-n)b时,方程组仅有零解.
(Ⅱ)当a+(n-1)b=0或a=b时,|A|=0,所给方程组有无穷多解.
①当a=b时,所给方程组与方程
x
1+x
2+x
3+…+x
n=0
同解,所以方程组的基础解系为:
α
1=(-1,1,0,…,0)
T,α
2=(-1,0,1,…,0)
T,…,α
n-1=(-1,0,0,…,1)
T,
故方程组的全部解是
x=c
1α
1+c
2α
2+…+c
n-1α
n-1,其中c
1,c
2,…,c
n-1,为任意常数.
②当a=(1-n)b且a≠b时,基础解系为:
β=(1,1,1,…,1)
T,
故方程组的全部解是
x=cβ,其中c为任意常数.
9. 设二次型f(x
1,x
2,x
3)=
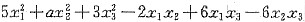
的矩阵合同于
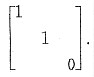
(Ⅰ)求常数a;
(Ⅱ)用正交变换法化二次型f(x
1,x
2,x
3)为标准型.
(Ⅰ)该二次型的矩阵为
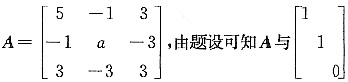
合同,所以r(A)=2,即有
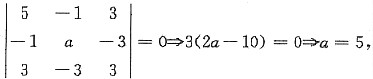
所以

(Ⅱ)由|λE-A|
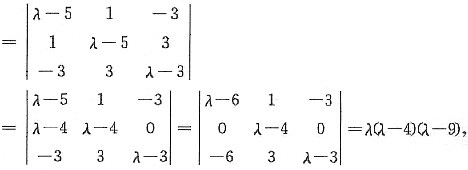
可得特征值λ
1=0,λ
2=4,λ
3=9.
由(0E-A)x=0可得属于0的特征向量
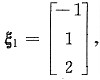
由(4E-A)x=0可得属于4的特征向量
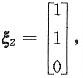
由(9E-A)x=0可得属于9的特征向量
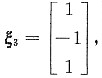
因为对实对称矩阵来讲,不同特征值对应的特征向量正交,所以只需单位化即可,

令Q=(η
1,η
2,η
3),x=Qy,
于是f(x
1,x
2,x
3)=
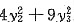
.
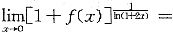 ______.
______.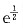
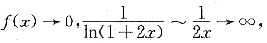
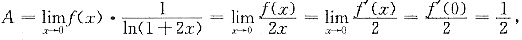
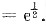
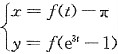 所确定,其中f可导,且f'(0)≠0,则
所确定,其中f可导,且f'(0)≠0,则
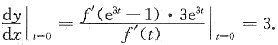
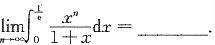
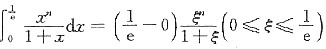 ,
,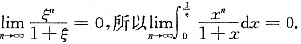
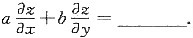
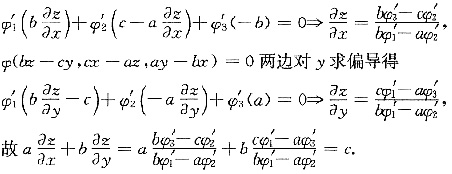
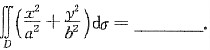
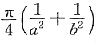
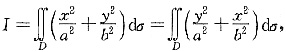
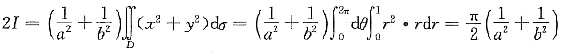 ,
,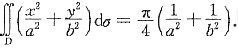
 |A|=|kA|,k>0,则k=______.
|A|=|kA|,k>0,则k=______.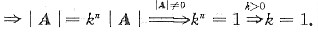
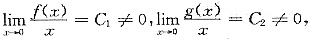
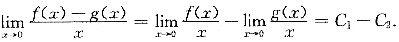

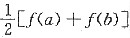
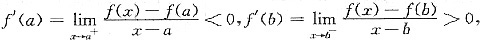
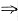 f'(0)f'(1)=-1<0.
f'(0)f'(1)=-1<0.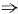 f'(0)f'(1)=-1<0,
f'(0)f'(1)=-1<0,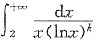 的敛散情况,下面判断正确的是______
的敛散情况,下面判断正确的是______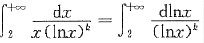
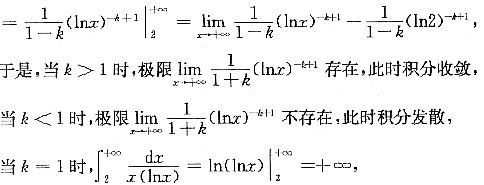

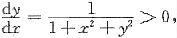 所以y=y(x)在(-∞,+∞)单调增加.
所以y=y(x)在(-∞,+∞)单调增加.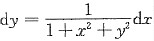 在[x0,x](x0<x)两边积分得
在[x0,x](x0<x)两边积分得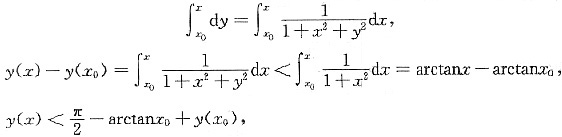
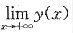 存在.
存在.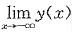 存在,故选C.
存在,故选C.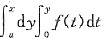 是x的奇函数.
是x的奇函数.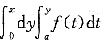 是x的奇函数.
是x的奇函数.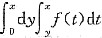 是x的奇函数.
是x的奇函数. 是x的奇函数.
是x的奇函数.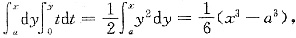 此式是否为奇函数与a有关,排除A.
此式是否为奇函数与a有关,排除A.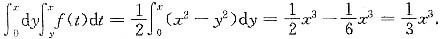
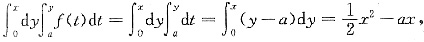 不是奇函数,可排除B.
不是奇函数,可排除B.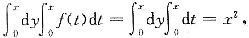 为偶函数,可排除D.
为偶函数,可排除D. 则在下列条件中使f(x1,y1)<f(x2,y2)成立的是______
则在下列条件中使f(x1,y1)<f(x2,y2)成立的是______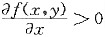 可知,固定y,f(x,y)关于x单调增加;
可知,固定y,f(x,y)关于x单调增加;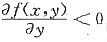 可知,固定x,f(x,y)关于y单调减少.
可知,固定x,f(x,y)关于y单调减少.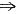 λ=0是A的一个特征值,
λ=0是A的一个特征值, Bx=0,则方程组Ay=0只有零解,此时r(A)=n,故选A.
Bx=0,则方程组Ay=0只有零解,此时r(A)=n,故选A.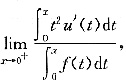 其中u(x)是曲线y=f(x)在x点处的切线在x轴上的截距.
其中u(x)是曲线y=f(x)在x点处的切线在x轴上的截距.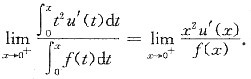
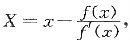 于是
于是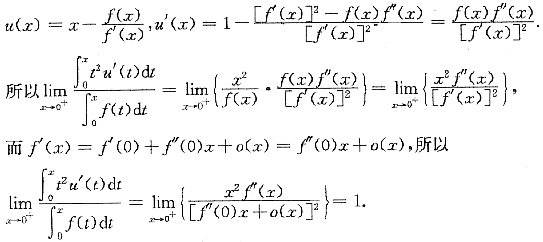
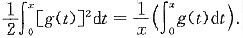
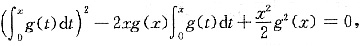
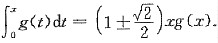
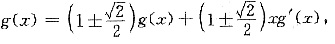
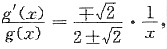 两边积分,
两边积分,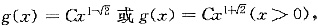 其中C为任意正数.
其中C为任意正数.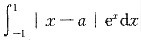 的最大值.
的最大值.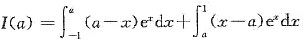 =-a(e+e-1)+2ea-2e-1
=-a(e+e-1)+2ea-2e-1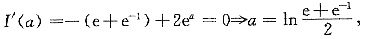
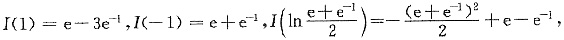
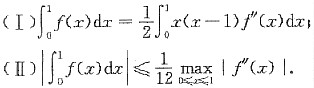
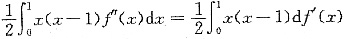
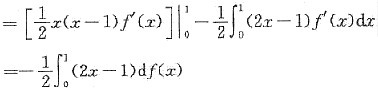
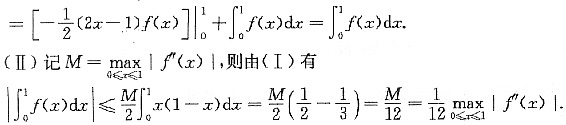
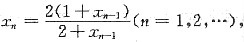 证明
证明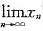 存在,并求之.
存在,并求之.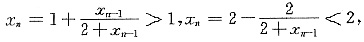
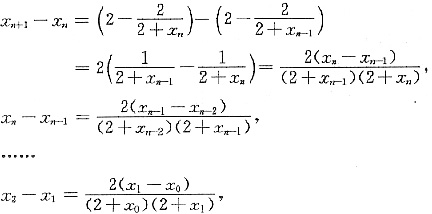
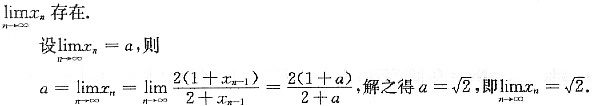
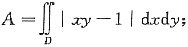
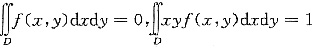 ,
,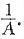
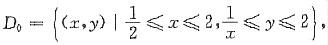 有
有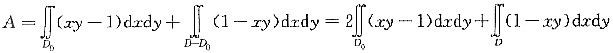
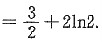
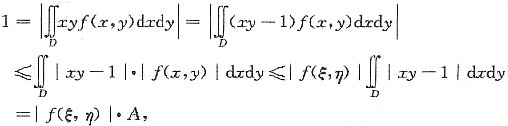
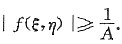
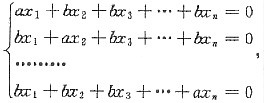
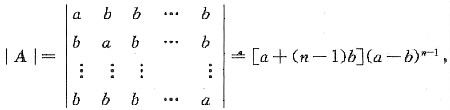
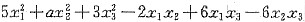 的矩阵合同于
的矩阵合同于

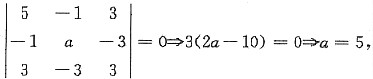

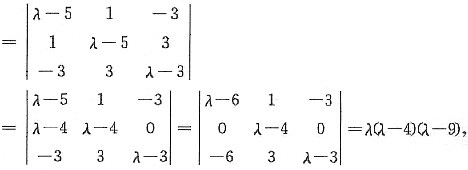
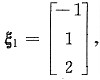
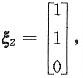


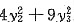 .
.