一、单项选择题2. 学校开展读好书活动,小华读一本共有n页的故事书,若第一天她读了全书页数的
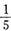
,第二天读了余下页数的
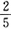
,则还没有读完的有______页。

A B C D
D
[解析] 一本书共n页,第一天读全书的
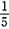
,剩下全书的
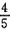
,第二天读余下的
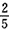
,没读的是余下的
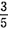
,则
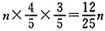
(页),故选D。
13. 已知点A(x
1,y
1)、B(x
2,y
2)在反比例函数
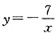
的图象上,且x
1<0<x
2,则y
1、y
2和0的大小关系______。
- A.y1>y2>0
- B.y1<y2<0
- C.y1>0>y2
- D.y1<0<y2
A B C D
C
[解析] 本题考查反比例函数性质,∵k=-7<0,∴该函数图象在二、四象限,∵x1<0<x2,∴在不同象限考虑,∴当x1<0时,y1>0,当x2>0时,y2<0,∴y1>0>y2。
二、填空题1. 已知关于x的分式方程
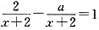
的解为负数,那么a的取值范围是______。
a>0且a≠2
[解析] 本题考查分式方程的解法和方程、不等式的解的意义。由
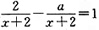
得,2-a=x+2,即x=-a,又因为x为负数且x≠-2,所以-a<0且-a≠-2,即a>0且a≠2。
2. 因式分解:9x
2-y
2-4y-4=______。
(3x-y-2)(3x+y+2)
[解析] 本题考查乘法公式的逆用。9x2-y2-4y-4=9x2-(y2+4y+4)=9x2-(y+2)2=(3x-y-2)(3x+y+2)。
3. 如图所示,已知线段DE由线段AB平移而得,AB=DC=4cm,EC=5cm,则ΔDCE的周长是______cm。
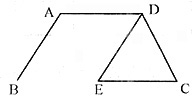
13
[解析] 本题考查平移的性质,平移不改变线段的长短,所以AB=DE所以ΔDCE的周长=4+4+5=13(cm)。
4. 如图所示,l
1是反比例函数
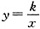
在第一象限内的图象,且过点A(2,1),l
2与l
1关于x轴对称,那么图象l
2的函数解析式为______(x>0)。
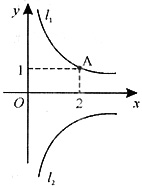
[解析] 本题考查平面直角坐标系中点的对称及待定系数法,将点A(2,1)代入函数
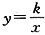
得:k=2,所以图象l
2的函数解析式为
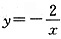
。
5. 一种产品的成本原来是p元,计划在今后m年内,使成本平均每年比上一年降低a%,则成本y与经过年数x的函数关系式为______。
y=p(1-a%)x,(1≤x≤m且x∈Z)
[解析] 经过1年,y=p(1-a%);经过2年,y=p(1-a%)-p(1-a%)a%=p(1-a%)(1-a%)=p(1-a%)2;经过3年,y=p(1-a%)2-p(1-a%)2a%=p(1-a%)3,故经过x年,y=p(1-a%)x,定义域的取值范围为:1≤x≤m且x∈Z。
6. 对任意整数A、B,规定A*B=2(A+B),则(2*3)*4=______。
28
[解析] 由A*B=2(A+B)知,2*3=2(2+3)=10,故(2*3)}4=10*4=2(10+4)=28。
7. 定义新运算“

”,
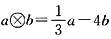
,则12

(-1)=______。
8
[解析] 根据已知条件可得,
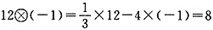
8. 口袋里有大小相同的8个红球和4个黄球,从中任意摸出1个球,摸出红球的可能性是______,摸出黄球的可能性是______。
[解析] 摸到红球的可能性为

,摸到黄球的可能性为
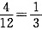
。
9. 若甲数除乙数的商是0.8,则甲、乙两数的比是______,如果甲数比乙数大0.8,则甲数是______。
10.
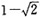
的相反数是______,倒数是______。
四、综合题1. 某农场要建一个长方形的鸡场,鸡场的一边靠墙,墙长25米,另三边用木栏围成,木栏长40米,求鸡场的最大面积是多少?
设垂直于围墙的木栏的边长为x米,那么平行于围墙的木栏的边长为(40-2x)米,则鸡场的面积为:
S=x(40-2x)=-2(x-10)
2+200。
∵0<x<20,且0<40-2x<25,则
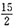
<x<20,
∴当x=10时,鸡场的面积最大,且最大值为200平方米。
鸡场的最大面积为200平方米。
2. 有一本书稿,用5号字排版印刷,每一页排26字×26行,即每一行26个字,共26行,共排了105页,排完后发现这种字太小,于是改为小四号字,每页排20字×21行,则该书印出后共有多少页?
改为小四号字后,该书的页数为:26×26×105÷20÷21=169。
该书改为小四号字以后,印出有169页。
3. 某电脑销售商试销某一品牌电脑(出厂价为3000元/台),以4000元/台销售时,平均每月可销售100台,现为了扩大销售,销售商决定降价销售,在原来1月份平均销售量的基础上,经2月份的市场调查,3月份调整价格后,月销售额达到576000元,已知电脑价格每台下降100元,月销售量将上升10台。
(1)求1月份到3月份销售额的月平均增长率;
(2)求3月份时该电脑的销售价格。
(1)设1月份到3月份销售额的月平均增长率为x,则有:
4000×100×(1+x)2=576000,
解得:x=20%。
所以1月份到3月份销售额的月平均增长率为20%。
(2)设3月份时该电脑的销售价格为m(3000<m<4000),则根据题意有:
[(4000-m)÷100×10+100]m=576000。
解得:x=3200或1800(舍去)。
所以3月份时该电脑的销售价格为3200元。
五、案例分析题1. 教学“乘数是三位数的乘法”时,原题的内容是一个粮店三月份售出面粉674袋,每袋25千克,一共售出面粉多少千克?这样一道例题让学生感觉与自己生活太远,和自己的关系又不是很密切,所以不能激发学生学习的兴趣,如果照着原例题讲,学生肯定会觉得枯燥无味,于是,我联系学生的生活来进行延伸,上课伊始,就让学生猜测一个滴水的水龙头每天要白白流掉多少千克水?学生们一听是生活中经常能遇到的事情,兴趣盎然,有的猜测5千克,有的猜测10千克,还有的猜测20千克,有个别学生看到了课后的内容说出来是12千克。教师接着问,照这样计算,一年要流掉多少千克水?学生马上算出平年是4380千克,闰年是4392千克,随着计算结果的出现,学生觉得非常吃惊:“哇!这么多呀!”看着学生吃惊的样子,教师又提出新的要求:“你家所住的楼房一共有多少户?如果按一家一个水龙头计算,一年要白白流掉多少水?”
请问:原题与改动后的题目比较有什么异同(包括与学生生活的联系、目标的维度、教学效果)?
“乘数是三位数的乘法”是一个比较抽象化的数学知识练习,但是它同样包含了丰富的过程性学习目标,教师在教学时应提供具体有趣的素材,引导学生通过观察、比较、思考,使学生获得“乘数是三位数的乘法”的学习体验,并掌握“乘数是三位数的乘法”算理。
从上面的两个情景中,我们可以看出第一个情景,由于学生缺乏真实的体验,缺少吸引学生的素材,学生很难对教材产生学习积极性,也不可能很好地参与学习的过程。
不少专家指出,“教科书,只是教与学的工具,绝不是唯一的资源”,“大胆而创造性地处理教材,甚至重组或改编教材,那是教师的业务权利”。因此,在第二个教学情景中,老师进行了大胆的替换改造,用学生熟悉的、感兴趣的、贴近学生实际的生活素材来取代。在上面的片段中,我们可以深刻感受到,学生已初步学会了用数学的思维方式去观察、分析周围的世界,并且在这个现实的、有意义的、富有挑战性的探究活动中,加深了对数学知识的理解与掌握,真正体会到了生活中充满了数学,感受到了数学的真谛与价值。
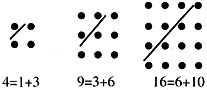
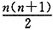 ,由此知9、16、18、31均不是“三角形数”,故选C。
,由此知9、16、18、31均不是“三角形数”,故选C。 ,第二天读了余下页数的
,第二天读了余下页数的 ,则还没有读完的有______页。
,则还没有读完的有______页。
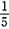 ,剩下全书的
,剩下全书的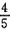 ,第二天读余下的
,第二天读余下的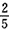 ,没读的是余下的
,没读的是余下的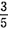 ,则
,则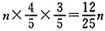 (页),故选D。
(页),故选D。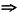 3(3b-2a+8)=54,即9b-6a+24=54,∴9b-6a+2=32,故选C。
3(3b-2a+8)=54,即9b-6a+24=54,∴9b-6a+2=32,故选C。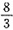
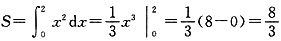 。故选B。
。故选B。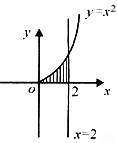
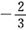 ,…的通项公式为______。
,…的通项公式为______。
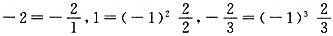 ,故该数列的通项公式为
,故该数列的通项公式为 ,故选C。
,故选C。
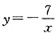 的图象上,且x1<0<x2,则y1、y2和0的大小关系______。
的图象上,且x1<0<x2,则y1、y2和0的大小关系______。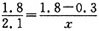 ,解得x=1.75。
,解得x=1.75。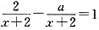 的解为负数,那么a的取值范围是______。
的解为负数,那么a的取值范围是______。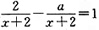 得,2-a=x+2,即x=-a,又因为x为负数且x≠-2,所以-a<0且-a≠-2,即a>0且a≠2。
得,2-a=x+2,即x=-a,又因为x为负数且x≠-2,所以-a<0且-a≠-2,即a>0且a≠2。
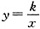 在第一象限内的图象,且过点A(2,1),l2与l1关于x轴对称,那么图象l2的函数解析式为______(x>0)。
在第一象限内的图象,且过点A(2,1),l2与l1关于x轴对称,那么图象l2的函数解析式为______(x>0)。

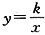 得:k=2,所以图象l2的函数解析式为
得:k=2,所以图象l2的函数解析式为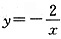 。
。 ”,
”,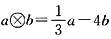 ,则12
,则12 (-1)=______。
(-1)=______。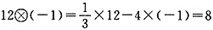
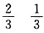
 ,摸到黄球的可能性为
,摸到黄球的可能性为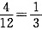 。
。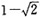 的相反数是______,倒数是______。
的相反数是______,倒数是______。
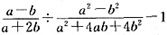 的值。
的值。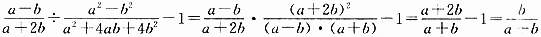
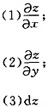
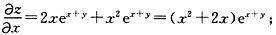
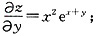
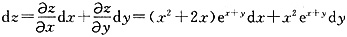
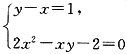
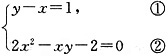

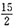 <x<20,
<x<20,