一、单项选择题在每小题列出的四个备选项中只有一个是符合题目要求的
2. 设函数f(x,y)=y
2-x
2+5,则点(0,0)______
- A.是f(x,y)的极小值点
- B.是f(x,y)的极大值点
- C.不是f(x,y)的驻点
- D.是f(x,y)的驻点但不是极值点
A B C D
D
[解析] 本题考查函数在某点是否取极值.
f(x,y)=y
2-x
2+5,
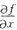
=-2x,
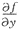
=2y,
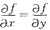
=0,则x=y=0.
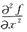
=-2,

=0,
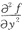
=2,所以△=0-(-2×2)=4≥0,所以(0,0)点不是f(x,y)的极值点,是f(x,y)的驻点,答案为D
3. 设区域D是由直线y=2x,y=3x及x=1所围成,则二重积分
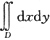
=______
A.
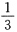
B.
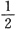
C.1 D.
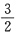
A B C D
B
[解析] 先画出区域D,如下图阴影部分,则
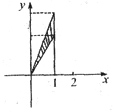
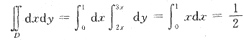
答案为B
4. 方程2y"+y'-y=2e
x的特解具有形式______
- A.aex+b
- B.aex
- C.ax2ex
- D.axex+bx
A B C D
B
[解析] 本题考查微分方程的特解形式,
由方程2y"+y'-y=2e
x知,其特征方程为2λ
2+λ-1=0,所以λ=
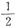
或-1,所以λ=1不是特征方程的根,所以特解形式应为ae
x,答案为B.
5. 若无穷级数
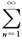
u
n收敛于S,则无穷级数
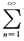
(u
n+1+u
n)收敛于______
A B C D
C
[解析]
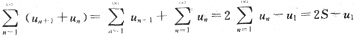
答案为C.
二、填空题在每小题的空格中填上正确答案
1. 设z=(1+xy)
x,则
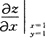
=______.
1+2ln2
[解析] 令1+xy=u,x=v,则
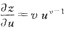
,
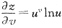
,
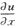
=y,
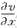
=1∴
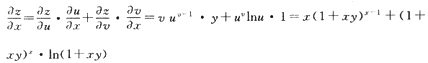
∴
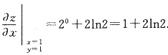
2. 设区域D:0≤x≤1,|y|≤2,则二重积分

(x+ysinx)dxdy的值等于______.
2
[解析]
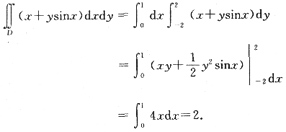
3.
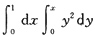
=______.
[解析]
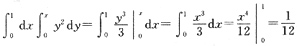
4. 微分方程
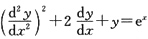
的阶数是______.
二阶
[解析] 微分方程的阶是指微分方程中出现的未知函数的最高阶导数的阶数,故该题的阶数为二阶.
5. 将函数f(x)=|x|在[-π,π]上展开成傅里叶级数,则傅里叶系数b
n=______.
0
[解析] f(x)为偶函数,故傅里叶级数为余弦级数,所以bn=0.
三、计算题1. 求过点P
1(1,2,-4)和P
2(3,-1,1)的直线方程.
直线的方向向量为
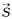
=(3-1,-1-2,1-(-4))=(2,-3,5)
∴
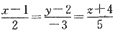
即为所求直线方程,也可用直线参数方程表示:
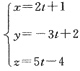
2. 求经过点P(3,0,-1),平行于平面π:3x-7y+5z-12=0的平面方程.
本题考查平面方程的求解.平面π的法向量为{3,-7,5},所求平画平行于平面π,于是其点法式方程为
3(x-3)-7y+5(x+1)=0,
即:3x-7y+5z-4=0
3. 已知方程x
2+y
2+z
2-8z=0确定函数z=z(x,y),求
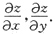
x
2+y
2+z
2-8z=0.
(1)
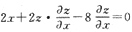
,
∴
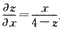
(2)
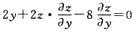
∴
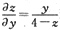
4. 求z=sinxcosy在点(
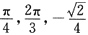
)的切平面与法线方程.
令F(x,y,z)=sinxcosy-z
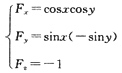
由题可知:
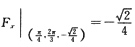
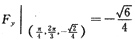
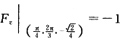
∴切平面为:
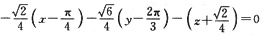
即:
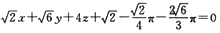
法线方程为:

5. 求曲线z=2x
2+3y
2在点(1,1,5)处的切平面方程.
对方程z=2x
2+3y
2求偏导有
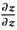
=1,
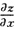
=4x,
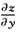
=6y.
则在点(1,1,5)处曲面切平面法向量为grad(1,1,5)=(4,6,1).
根据点法式方程有:
4(x-1)+6(y-1)+(z-5)=0,
整理得4x+6y+z=15.
6. D是由直线y=x,y=3x,x=1和x=3所围的区域用两种不同的方法来表达I=
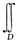
(x,y)dxdy.
7. 计算三重积分I=

xyzdxdydz,其中Ω是由平面x=1,y=1,z=1及坐标面所围成的区域.
8. 设L是圆周x
2+y
2+2y=0,求关于弧长的曲线积分
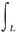
(y
2x+x
4)ds.
L的参数方程:
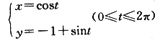
∴
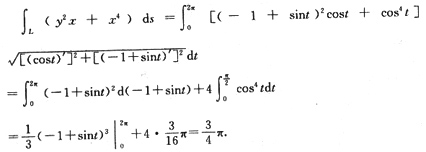
9. 计算对坐标的曲线积分
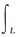
(x
2-2xy)dx+(y
2-2xy)dy,其中L为图中的有向折线ABO.
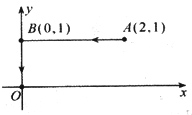
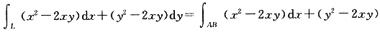
dy+
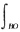
(x
2-2xy)+dx+(y
2-2xy)dy
∴在AB段dy=0,y=1,在BO段dx=0,x=0.
∴原式

10. 求微方程
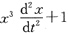
=0 x
(1)=1,x'
(1)=0的解.
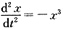
令
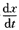
=p,则
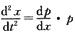
,代入上式得
dp
2=dx
-2 ∴
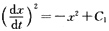
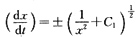
将初始条件代入上式得C
1=-1,所以
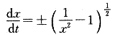
解之得x
2=1-(t+C
2)
2 再将x(1)=1代入上式得C
2=-1,所以方程的特解为x
2=1-(t-1)
2
11. 求幂级数
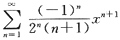
的收敛半径和收敛域.
∵
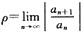
=
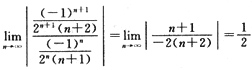
,
∴R=
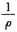
=2.
当x=2时,级数为
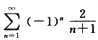
,为交错级数,收敛.
当x=-2时,级数为
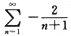
发散.
∴收敛域为(-2,2]
12. 求幂级数
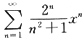
的收敛区间.
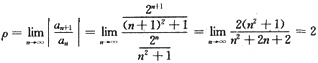
∴
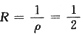
在x=
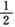
处,
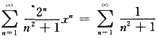
又因为
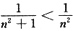
而级数
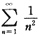
收敛.
由比较法知在x=
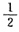
处级数收敛.
在x=-
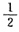
处,原级数为
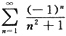
由上讨论知,级数绝对收敛.
四、综合题1. 求函数f(x,y)=x
3-4x
2+2xy-y
2+1的极值.
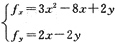
在f(x,y)取极值时:
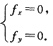
即:
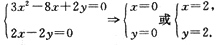
∴函数有两个极值f(0,0)=1,f(2,2)=-3分别为极大值与极小值.
2. 证明[y+ln(x+1)]dx+((x+1)-e
y)dy是某一函数u(x,y)的全微分,并求出u(x,y).
本题考查全微分的求解.原式在半平面x>-1上是某函数的全微分.取(x
0,y
0)为(0,0),积分路径取为如下图所示.折线ONM.
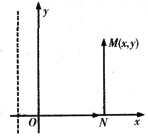
现令P(x,y)=y+ln(x+1)
Q(x,y)=x+1-e
y,则有
u(x,y)
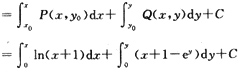
=(x+1)ln(x+1)-x+xy+y-e
y+1+C.
3. 将函数f(x)=
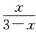
展开成x的幂级数.
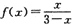
,f(0)=0,
f'(x)=
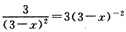
,f'(0)=3×3
-2 f"(x)=3×2(3-x)
-3,f"(0)=3×2×3
-3,
f"'(x)=3×3×2(3-x)
-4,f"'(0)=3×3×2×3
-4,
f
(4)(x)=3×4×3×2(3-x)
-6,f
(4)(0)=3×4×3×2×3
-5,

f
(n)(x)=3n!(3-x)
-n-1,
f
(n)(0)=3n!·3
-n-1=n!·3
-n.
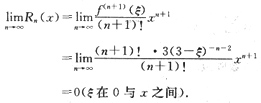
收敛半径R=
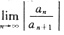
=
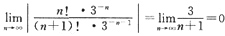
f(0)=f(0)x+
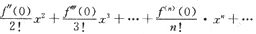
=3
-1x+3
-2x
2+3
-3x
3+…+3
-nx
n+…(收敛半径R=0).