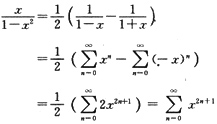一、单项选择题在每小题列出的四个备选项中只有一个是符合题目要求的
1. 平面π
1:x-4y+z+5=0与π
2:2x-2y-z+3=0的夹角θ=______
A.π B.
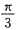
C.
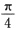
D.
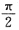
A B C D
C
[解析] 本题考查空间两平面的夹角.
由题意知平面π
1、π
2的法线向量分别为n
1={1,-4,1},n
2={2,-2,-1}.知|n
1|=
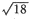
,|n
2|=3,n
1·n
2=2+8-1=9,所以cosα=
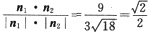
,所以
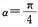
.答案为C
2. 设函数f(x,y)满足f
x(x
0,f
0)=f(x
0,y
0)=0,则函数f(x,y)在点(x
0,y
0)处______
- A.一定连续
- B.一定有极值
- C.一定可微
- D.偏导数一定存在
A B C D
D
[解析] 本题考查函数在某点处的性态.由二元函数连续可微的定义可知,fx(x0,y0)=fy(x0,y0)=0不能推出f(x,y)在点(x0,y0)处一定连续,可微.而fx(x0,y0)=fy(x0,y0)=0只是极值存在的必要条件,不能推出f(x,y)在点(x0,y0)处一定有极值.由偏导数的定义可知,D选项正确.答案为D.
3. 设B是圆形区域x
2+y
2≤4,则二重积分
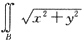
dxdy=______
A.
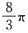
B.
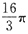
C.4π D.π
A B C D
B
[解析] 令x=rcosθ,y=rsinθ,则0≤θ≤2π,0≤r≤2∴
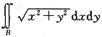
=
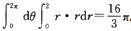
.答案为B.
5. 级数
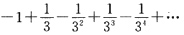
______
A.发散 B.收敛于-
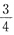
C.收敛于0 D.收敛于-
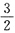
A B C D
B
[解析] 该级数是公比q=-
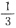
的等比级数,且|q|=
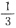
<1.故该级数收敛,且和为S=
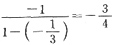
.答案为B.
二、填空题在每小题的空格中填上正确答案
1. 设函数z=arctan(x+y),则
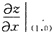
=______.
[解析]
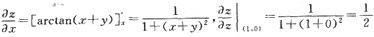
2. 设u=f(x)可导,则复合函数u=f(xyz)的全微分du=______.
yzf'(xyz)dx+xzf'(xyz)dy+xyf'(xyz)dz
[解析] 由题得
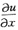
=f'(xyz)·yz,
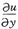
=f'(xyz)·xz,
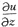
=f'(xyz)·xy
3. 已知sinxdx+cosydy是某个函数u(x,y)的全微分,则u(x,y)=______.
-cosx+siny+C
[解析] 根据全微分的定义,dz=
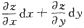
,则u(x,y)=∫sinxdx+∫cosydy=-cosx+siny+C.
4. 微分方程
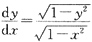
是______方程.
一阶可分离变量
[解析] 本题考查微分方程的定义.
由可分离变量微分方程的定义可知,
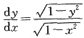
可化为
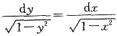
所以该方程为一阶可分离变量方程.
5. 设f(x)是周期为2π的周期函数,它在[-π,π)上表达式为f(x)=
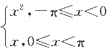
,s(x)是f(x)的傅里叶级数的和函数,则s(π)=______.
[解析] 因为f(x)是周期为2π的周期函数,可得x=π为f(x)的间断点,根据狄里克雷收敛准则,可得f(x)的傅里叶级数在x=π处收敛于
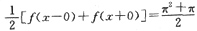
,即
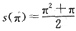
三、计算题1. 求与三个点A(3,7,-4),B(-5,7,-4),C(-5,1,-4)的距离都相等的点的轨迹.
本题考查空间中两点之间的距离轨迹.设满足题意的点为P(x,y,z),则应有
|AP|=|BP|=|CP|,
即|AP|
2=|BP|
2=|CP|
2.
又|AP|
2=(x-3)
2+(y-7)
2+(z+4)
2,
|BP|
2=(x+5)
2+(y-7)
2+(z+4)
2,
|CP|
2=(x+5)
2+(y-1)
2+(z+4)
2,
由|AP|
2=|BP|
2=|CP|
2化简得
-3x-7y+4z+37=5x-7y+4z+45
=5x-y+4z+21,
从而所求点的轨迹为
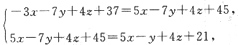
即
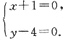
2. 设函数z=
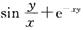
,求

.
4. 求函数f(x,y)=2xy-x
2-y
2在点(1,2)处,沿与x轴正向成60°角的方向l的方向导数.
l的方向单位向量
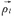
=(cosα,cosβ)=(cos60°,cos30°)=
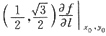
=f
x(x
0,y
0)cosα+f
y(x
0,y
0)cosβ
在点(1,2)处:f
x=
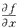
=2y-2x=2,f
y=
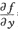
=2x-2y=-2.
∴所求方向导数
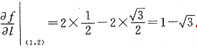
.
5. 求函数u=xyz沿从点(1,0,1)指向点(3,-1,3)的方向l的方向导数.
本题是有关方向导数的问题
u
x=yz,u
y=xz,u
z=xy,u
x(1,0,1)=0,u
y(1,0,1)=1,u
z(1,0,1)=0
由空间解析几何知识知,由点(1,0,1)到点(3,-1,3)的直线l的方向余弦为:
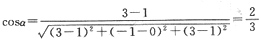
,
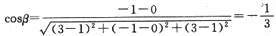
,
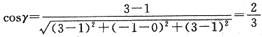
,
因此,
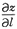
=u
x(1,0,1)cosα+u
y(1,0,1)cosβ+u
x(1,0,1)cosγ=-

.
6. 计算二次积分I=
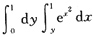
.
7. 计算I=

(x
2+y
2+z
2)dv,其。中Ω:x
2+y
2+z
2≤a
2.
积分域关于三个坐标面都对称,且被积函数是x、y、z的偶函数.
记Ω
1为Ω位于第一卦限的部分,则
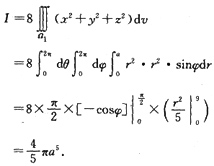
8. 计算对弧长的曲线积分
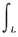
2xds,其中L是抛物线y=
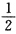
x
2上由点(1,
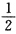
)到点(2,2)的一段弧.
9. 计算
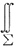
zdxdy+xdydz,其中∑是圆柱面x
2+y
2=1被z=0和z=3所截得部分的外侧.
原积分=
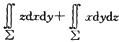
由于曲面∑(如下图所示)与xOy面垂直,所以∑在xOy面上投影的面积为零,故
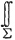
zdxdy=0.
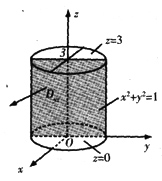
下面计算曲面积分
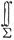
xdydz.将∑分成前后两片:∑=∑
1+∑
2,由∑的方程x
2+y
2=1(0≤z≤3)得,∑
1的方程为x=
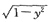
(-1≤y≤1);∑
2的方程为x=-
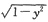
(-1≤y≤1).∑
1和∑
2在yOz面上的投影均为矩形区域D
yz:-1≤y≤1,0≤z≤3.由于∑
1和∑
2的法向量分别指向其投影坐标面yOz面的上、下方,故化为二重积分时分别取正号和负号.于是
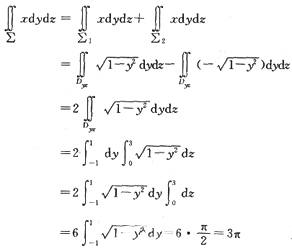
(其中由定积分的几何意义得
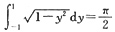
).(注:此题也可用高斯公式求解.)
10. 已知可导函数f(x)满足f(x)=1+

tf(t)dt,求函数f(x).
由f(x)=1+
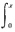
tf(t)dt,两边同时求导得:
f'(x)=xf(x),即
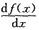
=xf(x)
∴
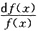
=xdx ∴
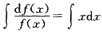
∴lnf(x)=
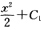
∴
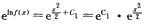
∴f(x)=
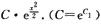
.
11. 判断级数
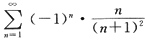
的敛散性.
令
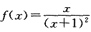
(x≥1),则

≤0,所以f(x)是[1,+∞]上的单调减函数,且
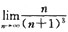
=0,故由莱布尼兹定理,知原级数收敛.
另一方面,因为
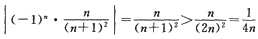
且
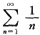
发散,故原级数非绝对收敛,
所以,原级数条件收敛.
12. 判断无穷级数
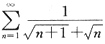
的敛散性.
四、综合题1. 求函数z=e
2x(x+y
2+2y)的极值.
本题考查多元函数极值的求解.
现令z=f(x,y)=e
2x(x+y
2+2y)
f'
x(x,y)=2e
2x(x+y
2+2y)+e
2x f'
y(x,y)=e
2x(2y+2)
令f'
x(x,y)=0,f'
y(x,y)=0
得:
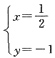
f'
xx(x,y)=2[2e
2x(x+y
2+2y)+e
2x]+e
2x =4e
2x(x+y
2+2y)+3e
2x f"
xy(x,y)=2e
2x(2y+2)=4e
2x(y+1)
f'
yy(x,y)=2e
2x A=f'
xx=(
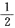
,-1)=e
B=f'
xy(
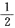
,-1)=0
C=2e
Δ=B
2-AC=0-e×2e=-2e
2<0
故(
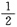
,-1)点为其极小值,
z(
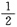
,-1)=-
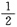
e.
2. 求由平面x=0,y=0,z=0,x+y=1及抛物面z=x
2+y
2所围成的曲顶柱体的体积.
3. 将函数
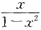
展开成x的幂级数,并求展开式成立的区间.
本题考查函数的幂级数展开.
已知
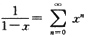
(1<x<1)将原函数化为
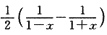
则