一、单项选择题5. 两条直线A
1x+B
1y+C
1=0,A
2x+B
2y+C
2=0垂直的充要条件是______
A.A
1A
2+B
1B
2=0 B.A
1A
2-B
1B
2=0
C.
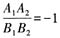
D.
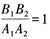
A B C D
A
[解析] 根据两直线垂直的充要条件斜率的积为-1可得答案。
8. 椭圆
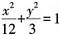
的左焦点为F
1,右焦点为F
2点P在椭圆上,如果线段PF
1的中点在y轴上,那么|PF
1|是|PF
2|的______
A B C D
B
[解析] 由题意知F
1(-3,0),F
2(3,0)。设点P(x
0,y
0),由线段PF
1的中点在y轴上知x
0=3,将其代入椭圆方程得
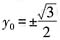
,所以
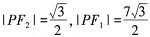
,即|PF
1|=7|PF
2|。
二、填空题1. 《普通高中数学课程标准(实验)》认为:学生的数学学习活动不应仅限于接受、记忆、模仿和练习,还应倡导自主探索、______、合作交流、______等学习方式。
动手实践;阅读自学
[解析] 高中数学课程还应倡导自主探索、动手实践、合作交流、阅读自学等学习数学的方式。这些方式有助于发挥学生学习的主动性,使学生的学习过程成为在教师引导下的“再创造”过程。
2. 高中数学课程的具体目标之一是:发展数学应用意识和______,力求对现实世界中蕴涵的一些______进行思考和作出判断。
创新意识;数学模式
[解析] 本题主要考查高中数学课程的具体目标。
3. (x+2)
10(x
2-1)的展开式中x
10的系数为(用数字作答)______。
179
[解析] 因为(x+2)
10(c
2-1)=x
2(x+2)
10-(x+2)
10,所以(x+2)
10(x
2-1)的展开式中x
10的系数是(x+2)
10展开式的x
8的系数减去x
10的系数。因为(x+2)
10展开式的通项为T
r+1=
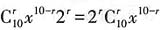
,所以令r=0,2分别得x
10,x
8的系数为1,180,故展开式中x
10的系数为180-1=179。
4. 球面上有3个点,其中任意两点的球面距离都等于大圆周长的
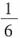
,经过这3个点的小圆的周长为4π,那么这个球半径为______。
[解析] 设球的球心为O,球面上三个点为A,B,C,由题意知三角形ABC为正三角形。设经过点A,B,C的小圆半径为r,则2πr=4π,所以r=2。在正三角形ABC中,应用正弦定理,得
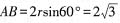
。因为
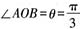
,所以侧面AOB是正三角形,得球半径R=OA=AB=
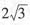
。
5.
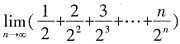
=______。
三、解答题1. 简述数学教学方法的选择依据。
教学的目的和任务,教材内容的特点,学生的实际情况,教师本身的素质,各种教学方法的职能、适用范围和使用条件,教学时间和效率的要求。
2. 怎样理解数学的抽象性?在数学教学中如何贯彻具体与抽象相结合的原则?
数学的抽象性:
(1)形式、数量关系的抽象;(2)比其他学科的抽象程度要高;(3)逐渐抽象的特点;(4)大量使用抽象符号。
贯彻具体与抽象相结合原则的方法:
(1)要着重培养学生的抽象思维能力。所谓抽象思维能力,是指脱离具体形象,运用概念、判断、推理等进行思维的能力。按抽象思维不同的程度,可分为经验型抽象和理论型抽象思维。在教学中,教师应着重发展理论型抽象思维,因为只有理论型抽象思维得到充分发展的人,才能很好地分析和综合各种事物,才有能力去解决问题。(2)要培养学生观察能力和提高抽象、概括能力。在教学中,可通过实物教具,利用数形结合,以形代数等手段。
3. 求积分

。
4. 求方程组的
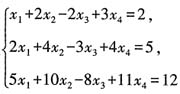
通解。
5. 双曲线
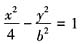
(b∈N
+)的焦点是F
1,F
2,P是双曲线上的一点,满足|OP|<5,且|PF
1|,|F
1F
2|,|PF
2|成等差数列,求此双曲线方程。
因为|PF
1|,|F
1F
2|,|PF
2|成等差数列,
所以2|F
1F
2|=|PF
1|+|PF
2|。①
又因为双曲线的焦点是F
1,F
2,P是双曲线上的一点,
所以||IPF
1|-|PF
2||=4。②
①
2+②
2得|PF
1|
2+|PF
2|
2=8+8c
2。③
设∠POF
1=0,∠POF
2=π-θ,
则|PF
1|
2=|PO|
2+|OF
1|
2-2|PO||OF
1|cos0,
|PF
2|
2=|PO|
2+|OF
22|
2-2|PO||OF
2|cos(π-θ),
所以|PF
1|
2+|PF
2|
2=2|PO|
2+2c
2,
联立③得2|PO|
2+2c
2=8+8c
2,
即|PO|
2=4+3c
2=4+3(4+b
2)=16+3b
2<25,即b
2<3.
又因为b∈N
+,所以b=1,即双曲线的方程为
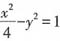
。
四、论述或案例设计题1. 试述数学概念的教学过程及一般方法,并就某一环节举例加以说明。
教学内容:
(1)概括。“概念形成主要依赖的是对感性经验的抽象概括,概念同化主要依赖的是感性经验的抽象概括。”(2)表述。对某类具有相同关键特征的事物命名,并使用学生能理解的方式陈述定义。(3)识别。在给出概念表述以后,教师应该区分学生对知识是真正理解,还是根据其无关特征回答有关概念的问题,教师可以举出一些与教材中叙述方式类似的新例子,帮助学生把握概念的关键特征,排除无关特征,从而真正地理解概念。(4)运用。已经获得的概念,可以在知觉水平上运用,也可以在思维水平上运用。
一般方法:
(1)生动恰当的引入概念。数学概念本是对事物特征的抽象概括,如果直接将抽象的文字语言呈现于学生面前进行概念教学,让学生死记硬背,将不利于学生对概念的理解和掌握。(2)丰富直观的背景材料。现实事物与旧概念均为直观的背景材料,而这两类都是学生对新概念从感觉到理性过渡的基础。(3)细致准确地讲解概念。①教师应从正面揭示概念的本质属性,准确地给概念下定义;②充分揭示概念的内涵与外延,应分清容易混淆的概念;③教师应讲解概念的确定性及某些概念的发展与深化。(4)运用多种形式巩固所学概念,帮助学生正确地运用概念。①及时复习整理;②使学生灵活运用概念。
2. 以“对数函数及其性质”为内容撰写一份说课稿。
各位老师,大家好!今天我说课的内容是人教版必修(一)对数函数及其性质第一课时,下面,我将从背景分析、教学目标设计、教辅手段、教学过程、教学评价设计五个方面对本课时的教学设计进行说明。
(1)背景分析
①学习任务分析。本节课主要学习对数函数的概念、图象和性质,求对数函数的定义域。对数函数是学生学习高中数学新教材引进的第二个基本初等函数,在学生学习指数函数和对数的运算后学习,本节课通过实际问题,引入对数函数,学生利用学习指数的方法来探索和研究对数函数的图象、性质,体会数形结合概括归纳的数学思想和方法,发展学生的数学思维能力。对数函数是本章一类重要函数,蕴涵着很重要的数学思想。根据课程标准我将本节课的重点确定为对数函数的概念、图象性质。
②学情分析。学生的基础较好,大多数学生的动手能力较好,因此可以通过描点,让学生动手画图象,观察图象的特征,进一步理解性质,因此我将本课的难点确定为用数形结合的方法从具体到一般地探索、概括对数函数的性质。
(2)教学目标设计
课程标准指出本节课的学习目标是:通过具体实例理解对数函数的概念,能借助计算机或计算器画出具体对数函数的图象,探索并理解对数函数的性质。所以本节课的教学目标为:①知识目标:理解指数函数的定义,掌握对数函数的图性质及其简单应用。②能力目标:通过教学培养学生观察问题、分析问题的能力,培养学生严谨的思维和科学正确的计算能力。③情感目标:通过学习,使学生学会认识事物的特殊与一般性之间的关系,构建和谐的课堂氛围,培养学生勇于提问、善于探索的思维品质。
(3)教辅手段
以学生独立思考、自主探究、合作交流,教师启发引导为主,以多媒体演示为辅的教学方法进行教学。
(4)教学过程
①创设情境,引入新课
本节课我是从在指数函数一节曾经做过的一道习题入手的。这样以旧代新逐层递近,不仅使学生易懂而且还体现了指对函数间的密切关系。我的引题是这样的:引题:一个细胞由一个分裂成两个,两个分裂成四个……依此类推,
A.求这样的一个细胞分裂的次数x与细胞个数y之间的函数关系式。
B.256个细胞是这个细胞经过几次分裂得到的?那么要得到1万、10万个细胞呢?第一问学生很容易得出是指数函数:y=2x。再看第二问,通过思考学生分析出这是个已知细胞个数求分裂次数的问题,即已知y求x的问题,即x=log2y,紧接着问学生:这是一个函数吗?将知识迁移到函数的定义,即对于任意一个y是否都有唯一的x与之相对应,为了万便学生理解,可以借助指数函数图象加以解释,得出x=log2y是一个函数,但它叉和我们平时所见过的函数形式上不一样,我们习惯上用x来表示自变量,y来表示函数,所以可将它改写成y=log2x,这样的函数称为对数函数。这便引出了本节课的课题。由于有了之前学习指数函数的基础,学生很容易就可归纳总结出:对数函数的一般形式:y=logax(a>0且a≠1),并求出定义域(0,+∞)。
②探究新知,加强理解
得到了对数函数的解析式,学生自然而然就会想到该研究它的图象了。我的想法是这样的:一方面描点法画图是学生需要熟练掌握的一类重要的画图方法,而且学生对自己画出的图象和归纳总结的知识记忆会更加深刻,所以我决定将课堂交给学生让他们自主探究,然后同学间互相讨论,并根据图象归纳出对数函数的性质。另一方面,研究对数函数图象主要是研究底数a对图象的影响,以及底数互为倒数的两个函数图象间的关系。我是用几何画板做了一个底数a变化时图象也随着变化的课件。通过底数a的变化,会出现不同的对数函数图象,学生会发现无论a怎样变化,图象的特点与由特殊函数总结出的规律一样,所以可以由特殊推出一般结论。还可以得出对数函数图象其实分为以下两类:a>1和0<a<1。然后让学生观察图象,类比指数函数的性质,自己归纳出对数函数的性质并总结在学案上。至此,对数函数的图象及性质就由教师引导,学生自主探究归纳总结出来。
 X
X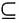 {1,2,3,4,5,6,7,8,9,10},那么这样的集合X有______
{1,2,3,4,5,6,7,8,9,10},那么这样的集合X有______
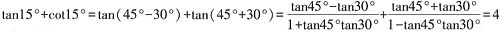 。
。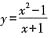 D.
D.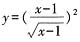

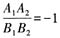 D.
D.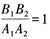


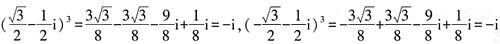 。
。 种。
种。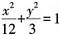 的左焦点为F1,右焦点为F2点P在椭圆上,如果线段PF1的中点在y轴上,那么|PF1|是|PF2|的______
的左焦点为F1,右焦点为F2点P在椭圆上,如果线段PF1的中点在y轴上,那么|PF1|是|PF2|的______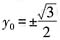 ,所以
,所以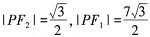 ,即|PF1|=7|PF2|。
,即|PF1|=7|PF2|。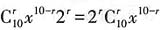 ,所以令r=0,2分别得x10,x8的系数为1,180,故展开式中x10的系数为180-1=179。
,所以令r=0,2分别得x10,x8的系数为1,180,故展开式中x10的系数为180-1=179。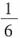 ,经过这3个点的小圆的周长为4π,那么这个球半径为______。
,经过这3个点的小圆的周长为4π,那么这个球半径为______。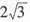
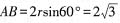 。因为
。因为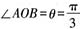 ,所以侧面AOB是正三角形,得球半径R=OA=AB=
,所以侧面AOB是正三角形,得球半径R=OA=AB=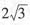 。
。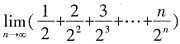 =______。
=______。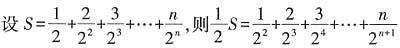 ,所以
,所以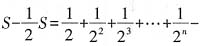

 。
。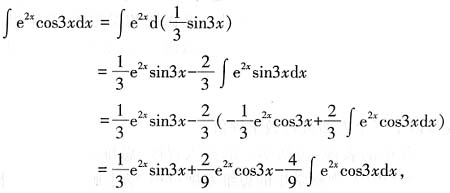
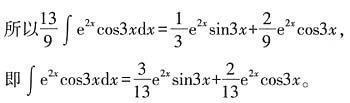
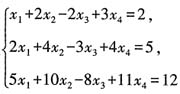 通解。
通解。 ,
,
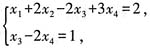
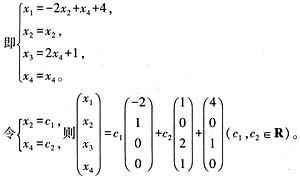
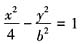 (b∈N+)的焦点是F1,F2,P是双曲线上的一点,满足|OP|<5,且|PF1|,|F1F2|,|PF2|成等差数列,求此双曲线方程。
(b∈N+)的焦点是F1,F2,P是双曲线上的一点,满足|OP|<5,且|PF1|,|F1F2|,|PF2|成等差数列,求此双曲线方程。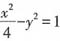 。
。