一、单项选择题4. 若关于x的方程式x
2+(1+2i)x-(3m-1)i=0有实根,则纯虚数m=______

A B C D
B
[解析] 设纯虚数m=ai,则方程可化为(x
2+x+3a)+(2x+1)i=0。若该方程有实数根,即2x+1=0,解得

,将其代入方程得
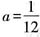
,则
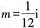
。
9. 双曲线的两个焦点是F
1,F
2,过F
1作垂直于实轴的弦PQ,若∠PF
2Q=90°,则该双曲线的离心率为______

A B C D
A
[解析] 设双曲线为
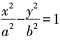
,所以|F
1F
2|=2c,|PF
2|-|PF
1|=2a。因为∠PF
2Q=90°,所以

,即
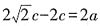
,解得
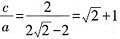
。
10. 若实数a,b满足a
2+ab-b
2=1,那么a
2+b
2的最小值是______

A B C D
B
[解析] 因为a
2+ab-b
2=1,所以a
2-b
2=1-ab,两边平方得a
4+b
4=3a
2b
2-2ab+1,即a
4+b
4+2a
2b
2=5a
2b
2-2ab+1,即
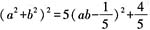
,所以当
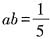
时,a
2+b
2的最小值为
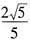
。
二、填空题1. 高中数学课程的具体目标之一是发展数学______和创新意识,力求对现实世界中蕴涵的一些______进行思考和作出判断。
应用意识;数学模式
[解析] 本题主要考查高中数学课程的具体目标。
2. 皮亚杰认为学生的认知发展水平可按年龄划分为四个阶段,即______、前运算阶段、具体运算阶段和______。
感觉运动阶段;形式运算阶段
[解析] 本题主要考查皮亚杰的认知发展理论。
3. 若函数y=log
2(ax
2+3x+1)的值域为R,则a的取值范围是______。
[解析] 由题意知ax
2+3x+1>0,当a=0时,不完全符合题意,舍去;当a<0时,也不完全符合题意;当a>0时,Δ=9-4a<0,解得
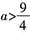
。综上,
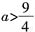
。
4.

=______。
xsinx+cosx+C
[解析]
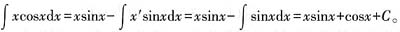
三、解答题1. 简述数学顺应学习的含义,并用适当的例子加以说明。
如果数学新知识在原有的数学认知结构中没有密切联系的适当知识,这时,如果要把新知识纳入到认知结构中,像同化学习那样通过与相关旧知识建立联系来获得新知识就比较困难。这时必须要对原有数学认知结构进行改组,使之与新知识内容相适应,从而把它纳入进去,这个过程叫做顺应。顺应学习主要是已有知识适应新知识的过程。例如,现在很多知识,都采用“树型结构”进行编排,这种“树型结构”就相当于我们头脑中的已有认知结构,当新知识产生后,如果新知识和原有认知结构里的旧知识没有联系,当新知识要被纳入原有“树型结构”时,就只能改变原有的结构,这就是顺应。又如,美国著名教育心理学家盖茨就曾经对教师提出如下建议:如果有人问,“你是教数学的吗?”最恰当的回答是:“我不是教数学的,我是教学生学数学的。”这就是我们平常所说的“授之以鱼,不如授之以渔”。
2. 简述《普通高中数学课程标准(实验)》所确定的课程基本理念。
(1)构建共同基础,提供发展平台;(2)提供多样课程,适应个性选择;(3)倡导积极主动、勇于探索的学习方式;(4)注重提高学生的数学思维能力;(5)发展学生的数学应用意识;(6)与时俱进地认识“双基”;(7)强调本质,注意适度形式化;(8)体现数学的文化价值;(9)注重信息技术与数学课程的整合;(10)建立合理、科学的评价体系。
3. 求函数f(x) =x
3-3x的极值。
f'(x)=3x2-3,
令f'(x)=0,得x=-l或1。
当x<-1时,f'(x)>0;当-1<x<1时,f'(x)<0;当x>1时,f'(x)>0。
所以当x=-1时,函数f(x)取得极大值,极大值为f(-1)=-1+3=2。
当x=1时,函数f(x)取得极小值,极小值为f(1)=1-3=-2。
4. 解线性方程组
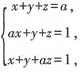
,其中a为常数。
线性方程组的增广矩阵为
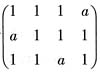
。

当a=1时,原线性方程组即x+y+z=1,有无数组解,
设y=w,z=v,则x=1-w-v,即
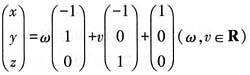
。
当a≠1时,增广矩阵可变换为

,
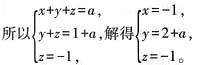
5. 已知椭圆

,A,B是椭圆上的两个点,线段AB的垂直平分线与x轴相交于点P(x
0,0),证明

。
设A,B的坐标分别为(x
1,y
1),(x
2,y
2),
因为线段AB的垂直平分线与x轴相交,
所以AB不平行于y轴,即x
1≠x
2。
又交点为P(x
0,0),所以|PA|=|PB|,
即
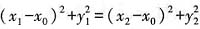
。①
∵点A,B在椭圆上,
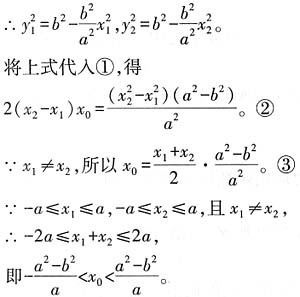
四、论述或案例设计题1. 试述数学思想方法教学的主要原则,并举例加以说明。
(1)目标性原则。遵循数学思想方法教学的目标性原则,首先,要明晰教材中所有数学思想方法,就目前共识的共有三大类18种,即策略思想方法,包括抽象概括、方程与函数、整体、化归、猜想;逻辑型思想方法,包括分类、类比、归纳、反证、演绎、特殊化;技巧型思想方法,包括换元、配方、待定系数、构造、参数、判别式。其次,对某些重要的数学思想方法进行分解、细化,使之明朗化,具有层次性。再次,在具体的每一节课教学中,数学思想方法教学目标应与课堂教学结构的各个重要环节相匹配,形成知识目标与思想方法目标的有机整合,使之具有可操作性。
(2)渗透性原则。遵循渗透性教学原则需做到以下两点:①挖掘渗透内容。教师只有认真钻研教材,才能正确地挖掘出课本知识中所蕴涵的数学思想方法,这是课堂教学中渗透数学思想方法的前提。②把握渗透的方法。在教学中,有机地结合数学表层知识的传授,恰当地渗透其中的数学思想方法,让学生在“数学知识的再发现”过程中享受“创造”或“发现”的愉悦,孕育数学发现的精神品质,这才是成功的渗透方法。
(3)层次性原则。数学思想方法的形成难于知识的理解和掌握,数学思想方法教学应与知识教学、学生认知水平相适应,数学思想方法教学应螺旋式上升、并遵循阶梯式的层次结构。
(4)概括性原则。所谓概括就是将蕴涵于数学知识体系中的思想方法归纳、提炼出来。在教学中,遵循概括性原则,将统摄知识的数学思想方法适时地概括出来,可以加强学生对数学思想方法的运用意识,也使其对运用数学思想方法解决问题的具体操作方式有更深入的了解,有利于活化所学知识,形成独立分析问题、解决问题的能力。概括数学思想方法一般可分两步进行:一是揭示数学思想方法的内容、规律,即将数学对象共同具有的属性或关系抽取出来,这也就是“概”字的含义;二是明确数学思想方法与知识的联系,即将抽取出来的共性推广至同类的对象上去,从而突出从特殊性认识上升为一般性认识。例如,通过解方程

,发现都可用换元法求解,在此基础上推广至x
2+
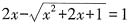
,也可用换元法求解。由此概括出换元法可以将复杂方程转化为简单方程,从而认识到化归思想方法是对换元法的高度概括,还可进一步认识到数学思想方法是数学的灵魂,它是对数学知识的高度概括。
2. 以“函数的奇偶性”为内容撰写一份说课稿。
我说课的内容是《函数的奇偶性》,下面我分别从教材分析、教学目标、教学重点和难点、教学方法和教学过程的设计这五个方面来叙述我对这节课的教学设想。
(1)教材分析
函数是中学数学的重点和难点,函数的思想贯穿于整个高中数学之中。函数的奇偶性是函数中的一个重要内容,它不仅与现实生活中的对称性有密切联系,而且为后面学习指数函数、对数函数、幂函数的性质做好了坚实的准备和基础。因此,本节课的内容是至关重要的,它对知识起到了承上启下的作用。
(2)教学目标
①知识目标:理解函数的奇偶性及其几何意义;学会运用函数图象理解和研究函数的性质;学会判断函数的奇偶性。
②能力目标:通过函数奇偶性概念的形成过程,培养学生观察、归纳、抽象的能力,渗透数形结合的数学思想。
③情感目标:通过函数的奇偶性教学,培养学生从特殊到一般的概括归纳问题的能力。
(3)教学重点和难点
教学重点:函数的奇偶性及其几何意义。
教学难点:判断函数奇偶性的方法与格式。
(4)教学方法
为了实现本节课的教学目标,在教法上我采取:在形成概念的过程中,紧扣概念中的关键语句,通过学生的主体参与,正确地形成概念。在鼓励学生主体参与的同时,不可忽视教师的主导作用,要教会学生清晰的思维、严谨的推理,并顺利地完成书面表达。
(5)教学过程
①引入课题
让学生画出函数f(x)=x2和f(x)=|x|的图象。(画图让学生巩固对二次函数和分段函数的画法)。
问题:这两个函数图象有什么共同特征吗?相应的两个函数值对应表是如何体现这些特征的?
答案:图象都关于y轴对称;自变量x取一对相反数时,相应的两个函数值相同。实际上,对于R内任意的一个x,都有f(-x)=x2=f(x),这时我们称函数f(x)=x2和f(x)=|x|都为偶函数。
②互动交流,研讨新知
函数的奇偶性定义中,注意:
A.函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是函数的整体性质;
B.由函数的奇偶性定义可知,函数具有奇偶性的一个必要条件是,对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量(即定义域关于原点对称)。
具有奇偶性的函数的图象的特征:偶函数的图象关于y轴对称;奇函数的图象关于原点对称。
③质疑问难,排难解惑,发展思维



 ,将其代入方程得
,将其代入方程得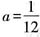 ,则
,则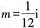 。
。 ,经过这三个点的小圆周长为4π,那么这个球的半径是______
,经过这三个点的小圆周长为4π,那么这个球的半径是______
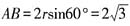 。因为
。因为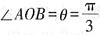 ,所以侧面AOB是正三角形,得球半径R=OA=AB=
,所以侧面AOB是正三角形,得球半径R=OA=AB=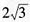 。
。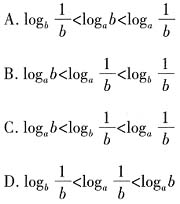
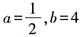 。
。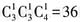 个;若百位数为2,4,则偶数有
个;若百位数为2,4,则偶数有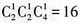 个。用0,1,2,3,4,5组成没有重复数字的三位数,其中排成偶数的方法共有36+16=52个。
个。用0,1,2,3,4,5组成没有重复数字的三位数,其中排成偶数的方法共有36+16=52个。
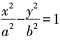 ,所以|F1F2|=2c,|PF2|-|PF1|=2a。因为∠PF2Q=90°,所以
,所以|F1F2|=2c,|PF2|-|PF1|=2a。因为∠PF2Q=90°,所以 ,即
,即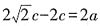 ,解得
,解得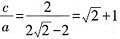 。
。
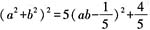 ,所以当
,所以当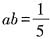 时,a2+b2的最小值为
时,a2+b2的最小值为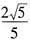 。
。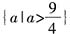
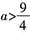 。综上,
。综上,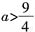 。
。 =______。
=______。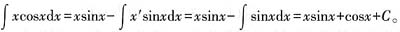
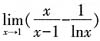 =______。
=______。
 =
=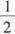
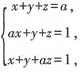 ,其中a为常数。
,其中a为常数。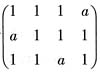 。
。
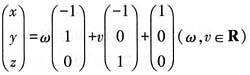 。
。 ,
,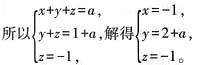
 ,A,B是椭圆上的两个点,线段AB的垂直平分线与x轴相交于点P(x0,0),证明
,A,B是椭圆上的两个点,线段AB的垂直平分线与x轴相交于点P(x0,0),证明 。
。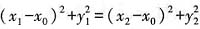 。①
。①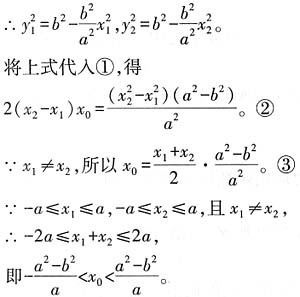
 ,发现都可用换元法求解,在此基础上推广至x2+
,发现都可用换元法求解,在此基础上推广至x2+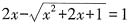 ,也可用换元法求解。由此概括出换元法可以将复杂方程转化为简单方程,从而认识到化归思想方法是对换元法的高度概括,还可进一步认识到数学思想方法是数学的灵魂,它是对数学知识的高度概括。
,也可用换元法求解。由此概括出换元法可以将复杂方程转化为简单方程,从而认识到化归思想方法是对换元法的高度概括,还可进一步认识到数学思想方法是数学的灵魂,它是对数学知识的高度概括。