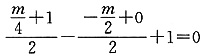一、问题求解下列每题给出的A、B、C、D、E五个选项中,只有一项是符合试题要求的。3. 已知关于x的一元二次方程x
2+2(m+1)x+(3m
2+4mn+4n
2+2)=0有实根,则m,n的值为______.
A.m=-1,
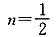
B.
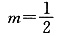
,n=-1
C.

,n=1 D.m=1,
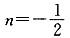
E.m=-1,
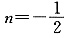
A B C D E
D
[解析] 方程有实根,则Δ≥0.可得
(m+1)
2-(3m
2+4mn+4n
2+2)≥0
2m
2+4mn+4n
2-2m+1≤0
即(m
2+4mn+4n
2)+(m
2-2m+1)≤0
(m+2n)
2+(m
2-1)
2≤0
所以当且仅当m=1且

时,不等式成立.
故正确答案为D.
4. 若直线l:
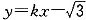
与直线2x+3y-6=0的交点位于第一象限,则直线l的倾斜角的取值范围是______.
A.
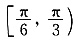
B.
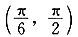
C.
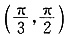
D.
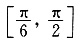
E.A、B、C、D都不正确
A B C D E
B
[解析] 求出交点坐标,再由交点在第一象限求得倾斜角的范围,
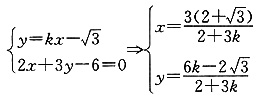
因为交点在第一象限,故
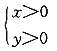
故
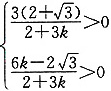
故
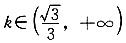
所以倾斜角的范围为
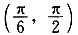
故正确答案为B.
10. 设等比数列{a
n}的前n项和为S
n,若S
3+S
6=2S
9,则数列的公比q为______.
A.
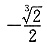
B.

C.
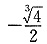
D.
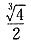
E.A、B、C、D都不正确
A B C D E
C
[解析] 若q=1,则有S
3=3a
1,S
6=6a
1,S
9=9a
1 但a
1≠0,即得S
3+S
6≠2S
9,与题设矛盾,故q≠1.
又依题意S
3+S
6=2S
9,可得
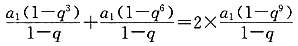
整理,得q
3(2q
6-q
3-1)=0,由q≠0,得方程2q
6-q
3-1=0
即(2q
3+1)(q
3-1) =0,因为q≠1,所以,q
3-1≠0
故

.
故正确答案为C.
注意:(1)要时刻注意公比q的取值范围,方能不断地简化计算;
(2)复数不能扩展到数列中,而
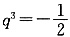
只有一个实数解.
11. 设{a
n}为等差数列,S
n为数列{a
n}的前n项和,已知S
7=7,S
15=75,T
n为数列
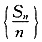
的前n项和,那么T
n=______.
A.
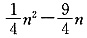
B.
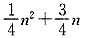
C.
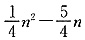
D.
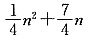
E.A、B、C、D都不正确
A B C D E
A
[解析] 设等差数列{a
n}的公差为d,则
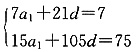
解得a
1=-2,d=1,故
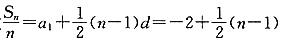
因为
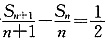
,故数列
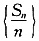
是首项为-2公差为
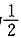
的等差数列,故
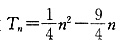
故正确答案为A.
12. 若不等式|ax+2|<6的解集为(-1,2),则实数a等于______.
- A.8
- B.2
- C.-4
- D.-8
- E.A、B、C、D均不正确
A B C D E
C
[解析] 由|ax+2|<6,得-6<ax+2<6,即-8<ax<4
若a>0,不等式解集为
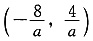
,则
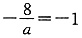
,且

,无解
若a<0,不等式解集为
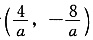
,则
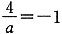
,且
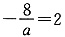
,得a=-4
故正确答案为C.
13. 不等式
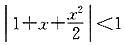
的解集是______.
A.{x|-1<x<0} B.
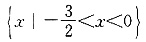
C.
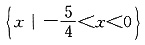
D.{x|-2<x<0}
E.A、B、C、D均不正确
A B C D E
D
[解析] 原不等式化为:
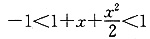
,即

①式化为x
2+2x+4>0,其解为x可取一切实数.
②式化为x
2+2x<0,其解为-2<x<0.
故原不等式的解集为{x|-2<r<0}.
故正确答案为D.
15. 甲、乙、丙三人完成某件工作,甲单独完成工作所用时间是乙、丙两人合作所需时间的4倍,乙单独完成工作所用的时间是甲、丙两人合作所需时间的3倍,则丙单独完成工作所需时间是甲、乙两人合作所需时间的______.
A.2 B.
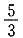
C.
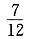
D.
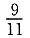
E.A、B、C、D均不正确
A B C D E
D
[解析] 此题为工程问题,当总工作量不具体时,通常设其为1.若某人需m天完成总工作量,则
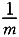
就是他的日工作量,或称为工作效率.工作效率与工作时间及工作量之间满足关系式:
工作量=工作效率×工作时间
此题可设甲、乙、丙单独完成工作所需时间分别为x,y,z,再设丙单独完成工作所需时间是甲、乙两人合作所需时间的a倍,a即为所求.
依题意,得
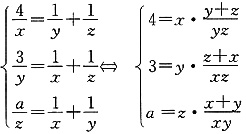
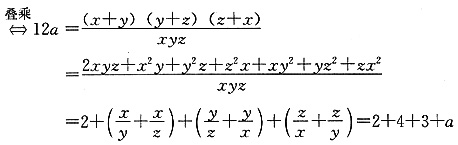
所以
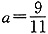
.
故正确答案为D.
三、逻辑推理下列每题给出的A、B、C、D、E五个选项中,只有一项是符合试题要求的。 以下是在一场关于“安乐死是否应合法化”的辩论中正反方辩手的发言:
正方:反方辩友反对“安乐死合法化”的根据主要是在什么条件下方可实施安乐死的标准不易掌握,这可能会给医疗事故甚至谋杀造成机会,使一些本来可以挽救的生命失去最后的机会。诚然,这样的风险是存在的。但是我们怎么能设想干任何事都排除所有风险呢?让我提一个问题,我们为什么不把法定的汽车时速限制为不超过自行车,这样汽车交通死亡事故发生率不是几乎可以下降到零吗?
反方:对方辩友把安乐死和交通死亡事故做以上的类比是毫无意义的。因为不可能有人会做这样的交通立法。设想一下,如果汽车行驶得和自行车一样慢,那还要汽车干什么?对方辩友,你愿意我们的社会再回到没有汽车的时代吗? 四、写作1. 论证有效性分析:分析下述论证中存在的缺陷和漏洞,写一篇600字左右的文章,对该论证的有效性进行分析和评论。
Apogee公司的业务集中在一个地方经营时,比现在更加有利可图。因此,Apogee公司应该关闭它在外地的办事处,在一个地方进行它所有的业务和经营。这种集中式经营将通过削减成本和帮助公司维持对于所有员工的更好的监督来改善公司的收益率。
在题干的论证中,作者认为Apogee公司应该关闭它在外地的办事处,在一个地方进行它所有的业务和经营,因为公司以前在一个地方经营时的利润比现在更高。由于以下几个原因,作者的论证并没有说服力:
第一,作者假设集中经营将通过削减成本和帮助公司维持对员工的更好的监督来改善公司收益率。然而,没有任何数据和实例能支持这一假设。此外,这种假设并没有考虑到集中式经营可能导致成本增加和降低效率。例如,公司的业务代表将不得不出差到那些以前由外地办事处负责的地区从事经营活动,这样就产生了出差成本,造成了重大的时间损失。简言之,这种假设必须依靠集中经营与现有的经营方式在成本与利润分析比较的支持。
第二,作者仅仅提供了唯一的原因,那就是当Apogee公司集中在一个地区经营时获利更多。但是过去利润率的提高仅仅是因为集中经营这种唯一的原因造成的吗?完全有可能是因为次品率高、产品价格定位不当、生产不充分、无效的广告、松弛的购买政策以及其他的浪费性支出过高等造成了经营不善的结果。如果作者不能排除其他能导致利润率递减的因素的话,那么作者的论证就会犯假设不当的错误,、这种假设认为一件事情发生后,另外一件事情会紧跟着发生,第一件事情是第二件事情发生的原因。
总之,题干的论证显得无力。为了加强Apogee公司应该关闭外地办事处,进行集中经营的结论,作者应该提供全面有效的成本与利润分析,除了集中经营可能影响当前的利润以外,排除其他的相关因素。
2. 论说文:根据下述材料,写一篇700字左右的论说文。题目自拟。
有这样一则寓言:虹看到弧形的桥,向它说,它的生命比自己长久。而桥却说:“你那么美丽,你在人们的记忆中必然是永恒的。”桥的话提示了我们:生命的价值不在于时间的长短,而在于所创造的价值。
擦出生命的火花
有这样一则寓言:虹看到弧形的桥,向它说,它的生命比自己长久。而桥却说:“你那么美丽,你在人们的记忆中必然是永恒的。”桥的话提示了我们:生命的价值不在于时间的长短,而在于所创造的价值。
七彩的虹存在的时间虽然很短,但它的光彩却引来天下人的瞩望和惊奇,给人们留下不可磨灭的印象,令人永远想到虹的光辉。古人说的“气贯长虹”,今人形容的“谁持彩虹当空舞”,都是对虹的真情赞美。可见,生命纵使短暂,假若能用这短暂的生命擦出火花,那这生命就是永存的。
生命不仅仅属于每个人自己,还属于他所处的社会。所以,人应该在有限的岁月中创造多一些的价值。夏完淳是我国历史上有名的英雄少年,最后慷慨就义,其生命虽短,精神却永远激励后人。英国的女作家夏洛蒂·勃朗特30多岁就离开了我们,可是那部世界著名的《简·爱》却永远流传在人们心中,放着光彩。
肉体是短暂的,精神是永存的。生命之美在于创造、奉献。以你的生命去投入吧,摩擦出生命的火花。像英勇牺牲的董存瑞,一心为人民服务的张秉贵,像呕心沥血的孔繁森,这些人正是在不同的时代里,利用有限的生命,全心奉献社会,擦出了生命中最美的火花。
像中国的屈原、司马迁、李白,像外国的歌德、但丁、普希金,全都创造了生命不能承受之美,他们的精神力量是强大的,超越了生命形式,给后人带来了最美的记忆。
“人固有一死,或轻于鸿毛,或重于泰山。”生命之美,在于你的社会价值的实现的程度。努力投入吧,努力奋斗吧,去创造出生命中最亮的火花。人的一生不可能成为一颗恒星,那就让我们在“岁月银河”中做一颗灿烂的流星;人不可能美好永驻,那就让我们做一支红烛,用光芒照亮别人。
愿人们都能擦出生命中最美的火花!
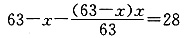
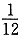 ,二队每天可完成乙工程的
,二队每天可完成乙工程的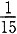 .雨天时,一、二队的工作效率分别为晴天时的60%和80%. 设雨天有x天,雨天工作量分别为
.雨天时,一、二队的工作效率分别为晴天时的60%和80%. 设雨天有x天,雨天工作量分别为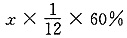 和
和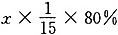 .那么晴天数为
.那么晴天数为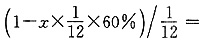
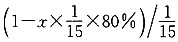 .解得x=15.
.解得x=15.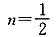 B.
B.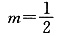 ,n=-1
,n=-1 ,n=1 D.m=1,
,n=1 D.m=1,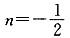
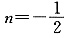
 时,不等式成立.
时,不等式成立.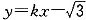 与直线2x+3y-6=0的交点位于第一象限,则直线l的倾斜角的取值范围是______.
与直线2x+3y-6=0的交点位于第一象限,则直线l的倾斜角的取值范围是______.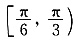 B.
B.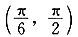 C.
C.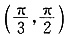
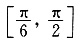 E.A、B、C、D都不正确
E.A、B、C、D都不正确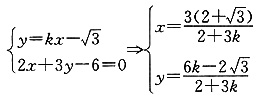
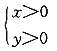
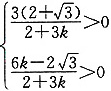
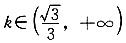
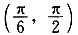
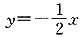 B.
B.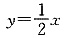 C.y=-2x
C.y=-2x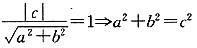
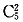 种方法,然后将这捆在一起的书连同其他3本共4个元素分给4个学生,有
种方法,然后将这捆在一起的书连同其他3本共4个元素分给4个学生,有 种分法,根据分步计数原理共有
种分法,根据分步计数原理共有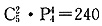 种不同的分法,
种不同的分法,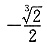 B.
B. C.
C.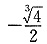
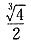 E.A、B、C、D都不正确
E.A、B、C、D都不正确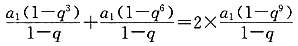
 .
.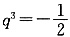 只有一个实数解.
只有一个实数解. 的前n项和,那么Tn=______.
的前n项和,那么Tn=______.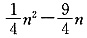 B.
B.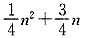 C.
C.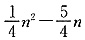
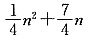 E.A、B、C、D都不正确
E.A、B、C、D都不正确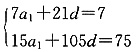
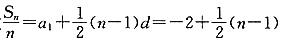
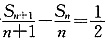 ,故数列
,故数列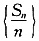 是首项为-2公差为
是首项为-2公差为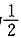 的等差数列,故
的等差数列,故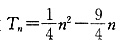
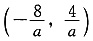 ,则
,则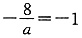 ,且
,且 ,无解
,无解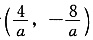 ,则
,则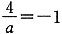 ,且
,且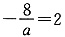 ,得a=-4
,得a=-4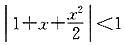 的解集是______.
的解集是______.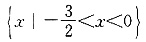
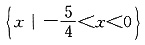 D.{x|-2<x<0}
D.{x|-2<x<0}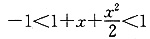 ,即
,即
 ,则甲的体积是乙的______.
,则甲的体积是乙的______. B.1倍 C.2倍
B.1倍 C.2倍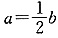 ,所以甲圆柱体的体积为
,所以甲圆柱体的体积为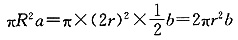
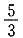 C.
C.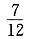
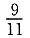 E.A、B、C、D均不正确
E.A、B、C、D均不正确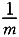 就是他的日工作量,或称为工作效率.工作效率与工作时间及工作量之间满足关系式:
就是他的日工作量,或称为工作效率.工作效率与工作时间及工作量之间满足关系式: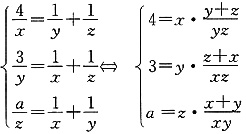
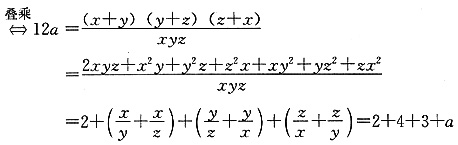
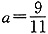 .
.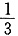
 的充分性.
的充分性.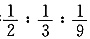 的比例分配贷款
的比例分配贷款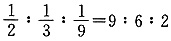 ,即条件(1)和条件(2)中的比例相等,
,即条件(1)和条件(2)中的比例相等,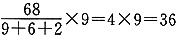 (万元)
(万元)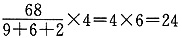 (万元)
(万元)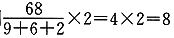 (万元)
(万元)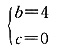 (2)b2-4c=16
(2)b2-4c=16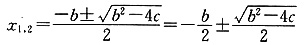
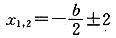
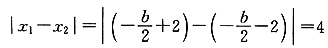
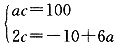
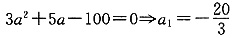 ,a2=5.根据题意,舍去a1,得到数列:5,10,20,30.满足结论.
,a2=5.根据题意,舍去a1,得到数列:5,10,20,30.满足结论.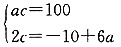
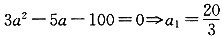 ,a2=-5. 根据题意,舍去a1,得到数列:-5,-10,-20,-30. 也满足结论,
,a2=-5. 根据题意,舍去a1,得到数列:-5,-10,-20,-30. 也满足结论,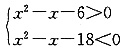
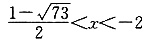 或
或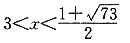
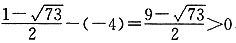 ,所以
,所以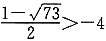 .
.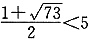 .
.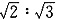
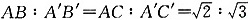 ,且∠A与∠A′互补
,且∠A与∠A′互补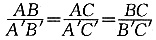
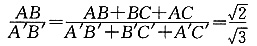
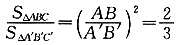
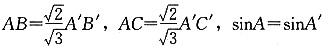
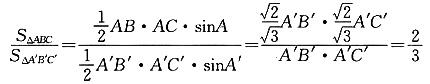
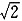
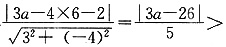 4,所以3a-26<-20或3a-26>20,解得a<2或
4,所以3a-26<-20或3a-26>20,解得a<2或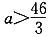 ,所以条件(1)不充分.
,所以条件(1)不充分.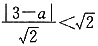 ,所以-2<a-3<2,即1<a<5,所以条件(2)充分,
,所以-2<a-3<2,即1<a<5,所以条件(2)充分,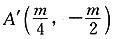
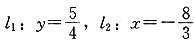 ,它们相互垂直.当m≠-3时,两条直线的斜率分别为
,它们相互垂直.当m≠-3时,两条直线的斜率分别为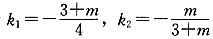 ,因为l1⊥l2,所以有
,因为l1⊥l2,所以有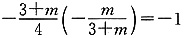 ,解得m=-4,所以条件(1)充分.
,解得m=-4,所以条件(1)充分.