一、单项选择1. 在

的展开式中,x
2x
3项的系数是______。
A B C D
D
[解析]
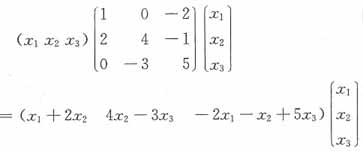
=(x
1+2x
2)x
1+(4x
2-3x
3)x
2-(2x
1+x
2-5x
3)x
3 含有x
2x
3的项为-3x
2x
3和-x
2x
3,因此x
2x
3项的系数是-4。
3. 行列式
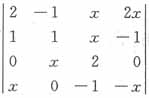
展开式中x
4的系数是______。
A B C D
B
[解析] 要使行列式
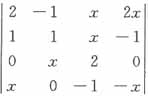
展开式中含x
4,则在行列式中,各不同的行、列都有x,即-(2x×x×x×x)=-2x
4(即对角线上都为x),故选B。
11. 已知4阶范德蒙行列式
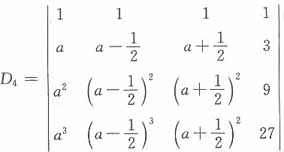
,则______。
A.当
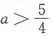
时,D
4>0 B.当

时,D
4>0
C.当
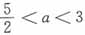
时,D
4>0 D.当a<3时,D
4<0
A B C D
C
[解析] 根据范德蒙行列式的计算式(或直接计算)得
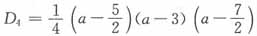
因为当
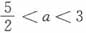
时,D
4>0,故正确答案为C。
13. 设

,则A
21+3A
22+2A
23=______。
A B C D
A
[解析] 构造一个新的行列式
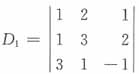
虽然D与D
1不同,但这两个行列式的代数余子式A
21,A
22,A
23是一样的,要计算行列式D的代数余子式A
21,A
22,A
23的和可以通过行列式D
1来实现,一方面,对行列式D
1按第2行展开,有
D
1=A
21+3A
22+2A
23 另一方面,对D
1计算,有

从而,得A
21+3A
22+2A
23=1
故正确答案为A。
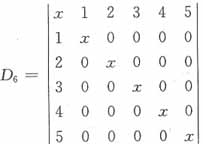
15. 计算行列式

______。
A.

B.
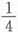
C.
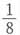
D.
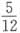
A B C D
A
[解析] 简化计算可先利用行列式的性质去掉行列式里的分母,转化为整数的运算
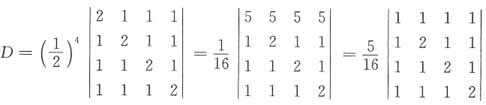

故正确答案为A。
16. 计算行列式
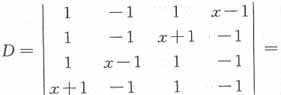
______。
A.x
2 B.x
3 C.x
4 D.
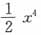
A B C D
C
[解析] 每行均是一个x,两个1与两个-1,那么各列式均加至第1列,则第1列有公因数x,然后把第1列加至第2列与第4列,第1列的-1倍加至第3列,即可三角化
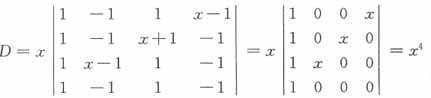
故正确答案为C。
18. 已知3阶行列式
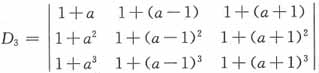
,则______。
- A.当a=1时,D3>0
- B.当a=-4时,D3=0
- C.当a>2时,D3>0
- D.当a>0时,D3>0
A B C D
B
[解析] 用加边法求D
3 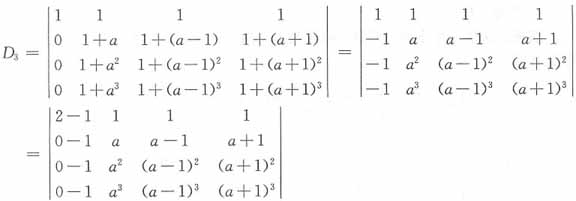
=2a(a-1)(a+1)(-1)·2-(a-1)(a-2)a(-1)·1·2
=-2(a-1)a[2(a+1)-(a-2)]=-2(a-1)a(a+4)
故当a=-4时,D
3=0,故正确答案为B。
21.
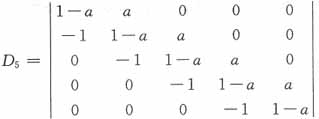
,则不正确的结论是______。
- A.当a=0时,D5=1
- B.当a=1时,D5=0
- C.当a=2时,D5=-1
- D.当a=-1时,D5=6
A B C D
C
[解析] 把行列式的各列加到第1列上,再按第1列展开得

其中D
4是同类项的行列式,用同样方法可得到
D
4=D
3+(-1)
5(-a)a
3=D
3+a
4 D
3=D
2+(-1)
4(-a)a
2=D
2-a
3 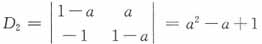
代入得D
5=1-a+a
2-a
3+a
4-a
5 当a=0时,D
5=1,故A正确;
当a=1时,D
5=0,故B正确;
当a=2时,D
5=-21,故C不正确;
当a=-1时,D
5=6,故D正确。
故正确答案为C。
23. 三元一次方程组
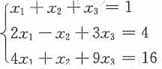
的解中,未知数x
2的值必为______。
A.1 B.
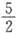
C.
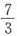
D.
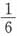
A B C D
D
[解析] 因为方程组的系数矩阵是范德蒙行列式,则有
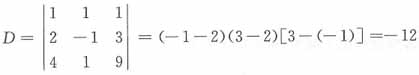
根据克莱姆法则,
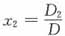
,其中
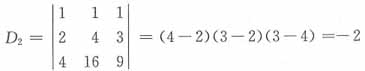
可知
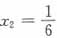
,故正确答案为D。
24. 设
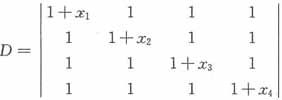
,则不正确的结论是______。
- A.当x2=0时,D=x1x3x4
- B.当x3=0时,D=x1x2x4
- C.当x4=0时,D=x1x2x3
- D.当x1x2x3x4≠0时,D=x1x2x3+x1x2x4+x1x3x4+x2x3x4
A B C D
D
[解析] 把行列式的第一行乘(-1)分别加到第2,3,4行上,得
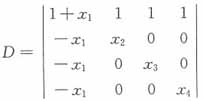
故得D=x
1x
2x
3x
4+x
1x
2x
3+x
1x
2x
4+x
1x
3x
4+x
2x
3x
4 当x
2=0时,代入得D=x
1x
3x
4,A正确;
当x
3=0时,代入得D=x
1x
2x
4,B正确;
当x
4=0时,代入得D=x
1x
2x
3,C正确;
当x
1x
2x
3x
4≠0时,显然D不正确。
故正确答案为D。
25. 齐次线性方程组
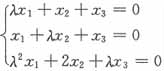
有非零解,则λ=______。
- A.1,2,3
- B.1,2
- C.-1,2
- D.1,-2,3
A B C D
B
[解析] x
1=0,x
2=0,x
3=0必是齐次线性方程组的解,现在方程组又有非零解,说明方程组的解不唯一,那么由克莱姆法则必有系数行列式为0,
因为
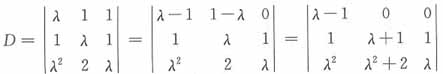
=(λ-1)(λ-2)
故λ为1或2,故正确答案为B。
28.

______。
A.
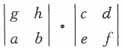
B.
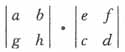
C.

D.
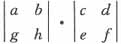
A B C D
D
[解析]
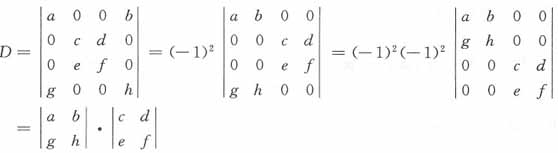
故正确答案为D。
35. 设n阶(n≥3)行列式|A|=a,将|A|每一列减去其余的各列得到的行列式为|B|,则|B|=______。
- A.a(n-2)2n-1
- B.a(2-n)2n-1
- C.a(n-2)22n-1
- D.a(2-n)22n-1
A B C D
B
[解析] 设A=(α
1,α
2,…,α
n),其中α
i(i=1,2,…,n)为n维列向量,则

故


故正确答案为B。
37. 已知
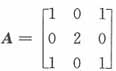
,且满足AX+I=A
2+X,那么矩阵X=______。
A.

B.

C.

D.

A B C D
A
[解析] 由AX+I=A
2+X,移项整理,得
(A-I)X=A
2-I=(A-I)(A+I)
因为

,故A-I可逆,用(A-I)
-1左乘上式两端,得
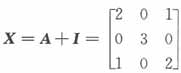
故正确答案为A。
39. 设A、B都是n阶矩阵,以下各式不正确的是______。
- A.|A+B|=|A|+|B|
- B.|ABT|=|A||B|
- C.||A|B|=|A|n|B|
- D.|A+B||A-B|=|A-B||A+B|
A B C D
A
[解析] |A+B|=|A|+|B|不正确,例如
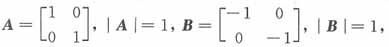
而
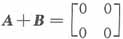
,|A+B|=0,|A|+|B|=2
选项B中,|AB
T|=|A||B
T|=|A||B|;
选项C中,||A|B|=|A|
n|B|,|A|B相当于数|A|乘B;
选项D中,|A+B|与|A-B|为两个数,相乘可交换,因此,B、C、D均正确,故正确答案为A。
 的展开式中,x2x3项的系数是______。
的展开式中,x2x3项的系数是______。 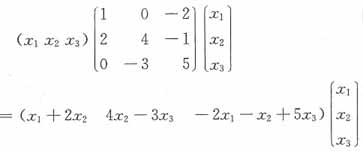
 展开式中的常数项为______。
展开式中的常数项为______。 中的x均为零时,结果即为常数项,即常数项=
中的x均为零时,结果即为常数项,即常数项= =0,故应选D。
=0,故应选D。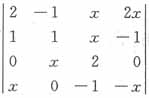 展开式中x4的系数是______。
展开式中x4的系数是______。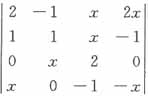 展开式中含x4,则在行列式中,各不同的行、列都有x,即-(2x×x×x×x)=-2x4(即对角线上都为x),故选B。
展开式中含x4,则在行列式中,各不同的行、列都有x,即-(2x×x×x×x)=-2x4(即对角线上都为x),故选B。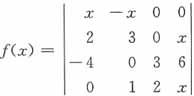 ,则f'(0)=______。
,则f'(0)=______。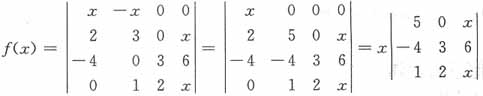
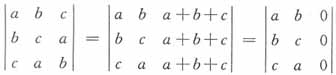 =0。故选B。
=0。故选B。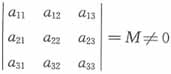 ,则行列式
,则行列式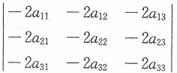 =______。
=______。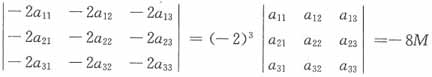
 ______。
______。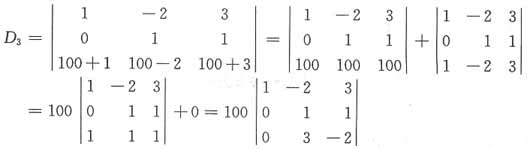
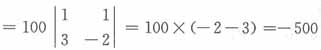
 ______。
______。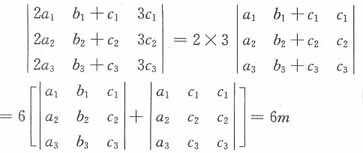
 的值为______。
的值为______。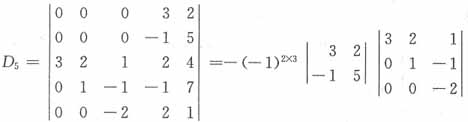
 ,则______。
,则______。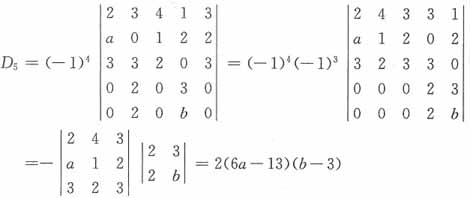
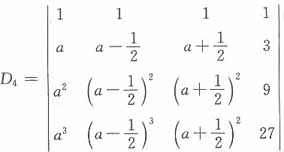 ,则______。
,则______。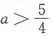 时,D4>0 B.当
时,D4>0 B.当 时,D4>0
时,D4>0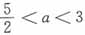 时,D4>0 D.当a<3时,D4<0
时,D4>0 D.当a<3时,D4<0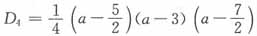
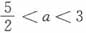 时,D4>0,故正确答案为C。
时,D4>0,故正确答案为C。 ,则
,则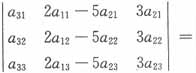 ______。
______。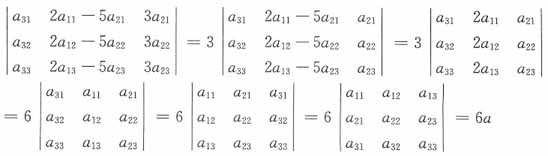
 ,则A21+3A22+2A23=______。
,则A21+3A22+2A23=______。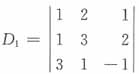

 ,则______。
,则______。
 ______。
______。 B.
B.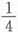 C.
C.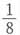 D.
D.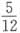
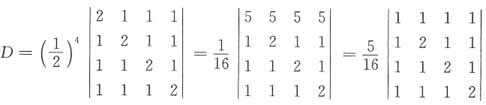

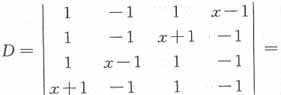 ______。
______。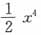
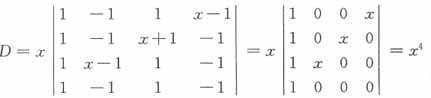
 ,则x=______。
,则x=______。 ,由此得-4(5x-12)=8,解得x=2
,由此得-4(5x-12)=8,解得x=2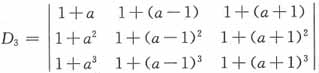 ,则______。
,则______。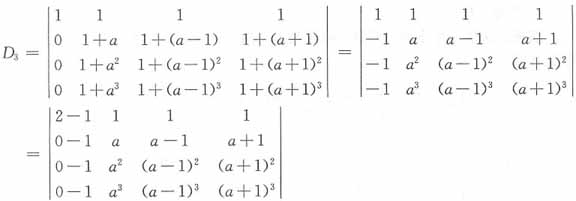
 的根x=______。
的根x=______。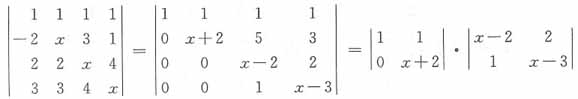
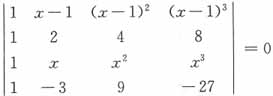 ,根的个数为______。
,根的个数为______。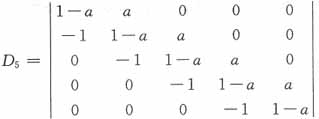 ,则不正确的结论是______。
,则不正确的结论是______。
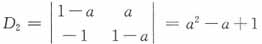
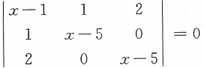 的三个根是______。
的三个根是______。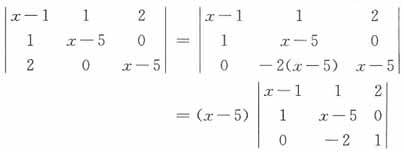
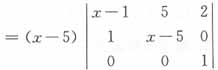
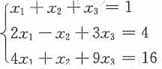 的解中,未知数x2的值必为______。
的解中,未知数x2的值必为______。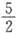 C.
C.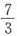 D.
D.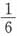
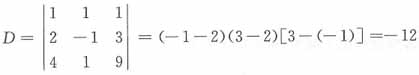
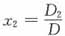 ,其中
,其中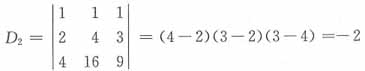
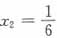 ,故正确答案为D。
,故正确答案为D。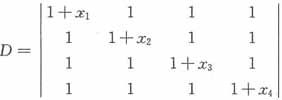 ,则不正确的结论是______。
,则不正确的结论是______。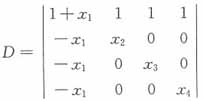
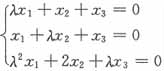 有非零解,则λ=______。
有非零解,则λ=______。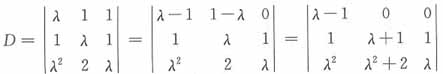
 的值为______。
的值为______。
 ______。
______。
 ______。
______。 B.
B.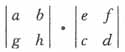
 D.
D.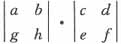
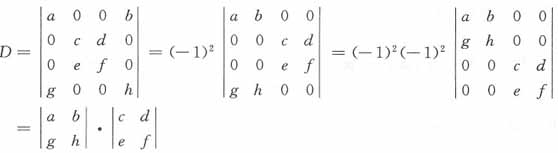
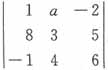 的代数余子式A21=4,则a=______。
的代数余子式A21=4,则a=______。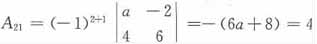
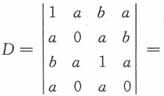 ______。
______。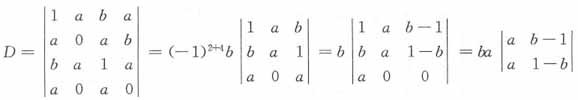
 ______。
______。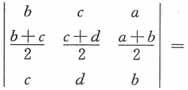 ______。
______。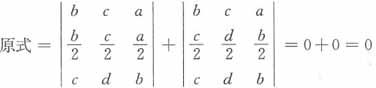
 ______。
______。 (范德蒙行列式)
(范德蒙行列式) ______。
______。



 的值为______。
的值为______。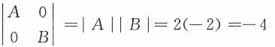
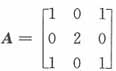 ,且满足AX+I=A2+X,那么矩阵X=______。
,且满足AX+I=A2+X,那么矩阵X=______。



 ,故A-I可逆,用(A-I)-1左乘上式两端,得
,故A-I可逆,用(A-I)-1左乘上式两端,得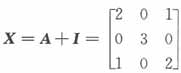
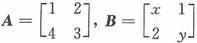 ,则当x与y满足关系式______时,AB=BA。
,则当x与y满足关系式______时,AB=BA。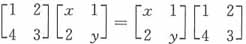
 ,由矩阵对应元素相等,得y=x+1,故正确答案为B。
,由矩阵对应元素相等,得y=x+1,故正确答案为B。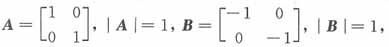
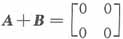 ,|A+B|=0,|A|+|B|=2
,|A+B|=0,|A|+|B|=2 ,那么r(A)=______。
,那么r(A)=______。
