一、单项选择题2. 若A={x|x
2=1},B={x|x
2-2x-3=0},则A∩B=______。
A.{3} B.{1}
C.
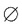
D.{-1}
A B C D
D
[解析] ∵A={x|x=-1,x=1},B={x|x=-1,x=3},∴A∩B={-1}。故选D。
5. 若圆x
2+y
2-4x-4y-10=0上至少有3个不同的点到直线l:ax+by=0的距离为
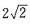
,则直线l的倾斜角的取值范围是______。
A.
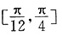
B.
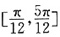
C.

D.
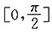
A B C D
B
[解析] (x-2)
2+(y-2)
2=18是以(2,2)为圆心,
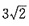
为半径的圆,ax+by=0是一过原点的直线。当圆心到直线距离小于或等于

时,能够满足题意。设y=kx为直线方程,∴
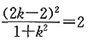
∴
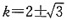
。设倾斜角为β,则
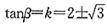
,解得
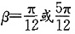
。故选B。
10. 已知向量
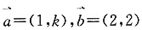
,且

与
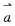
共线,那么
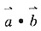
的值为______。
A B C D
D
[解析]
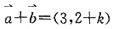
,∵

与
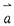
共线,∴3×2-(2+k)×2=0,解得k=1,
∴
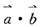
=1×2+1×2=4。故选D。
11. 假设200件产品中有3件次品,现在从中任取5件,其中至少有2件次品的抽法有______。
A.
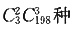
B.

C.

D.
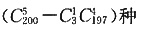
A B C D
B
[解析] 分两种情况,有2件次品的抽法

种,有3种次品的抽法
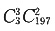
种。故选B。
12. 一个小组有6人,任选2名代表,求其中某甲当选的概率是______。
A.
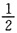
B.
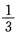
C.

D.

A B C D
B
[解析]
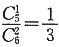
。故选B。
15. 若ξ~B(5,0.1),那么P(ξ≤2)等于______。
- A.0.0729
- B.0.00856
- C.0.91854
- D.0.99144
A B C D
D
[解析] P(ξ≤2)=P(ξ=0)+P(ξ=1)+P(ξ=2)=
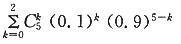
=(0.9)
5+5·(0.1)·(0.9)
4+

·(0.1)
2·(0.9)
3 =0.59049+0.32805+0.0729=0.99144。故选D。
二、填空题1. (1+2x)
6的展开式中x
4的系数是______。
2. 若
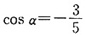
,且

,则tanα=______。
3. 过原点的直线与圆x
2+y
2-2x-4y+4=0相交所得的弦长为2,则该直线的方程为______。
4. 从甲、乙等10位同学中任选3位去参加某项活动,则所选3位中有甲但没有乙的概率为______。
5. 若实数a、b、c满足2
a+2
b=2
a+b,2
a+2
b+2
c=2
a+b+c,则c的最大值是______。
6. 已知:x、y∈(0,+∞),且log
2x+log
2y=2,则
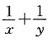
的最小值是______。
7. 设集合A={a|a=3n+2,n∈Z},集合B={b|b=3k-1,k∈Z},则集合A、B的关系是______。
8. 如图△ABC中,∠B=90°,∠C=30°,AB=1,将△ABC绕顶点A旋转180°,点C落在C'处,则CC'的长为______。
9. 下图是引拉线固定电线杆的示意图。已知:CD⊥AB,

,∠CAD=∠CBD=60°,则拉线AC的长是______m。
10. 若三点A(2,2),B(a,0),C(0,b)(ab≠0)共线,则

的值等于______。
三、解答题1. 某学生语、数、英三科考试成绩,在一次考试中排名全班第一的概率:语文为0.9,数学为0.8,英语为0.85,问一次考试中
(1)三科成绩均未获得第一名的概率是多少?
(2)恰有一科成绩未获得第一名的概率是多少?
分别记该生语、数、英考试成绩排名全班第一的事件为A、B、C
则P(A)=0.9,P(B)=0.8,P(C)=0.85
(1)

=[1-P(A)][1-P(B)[1-P(C)]=(1-0.9)(1-0.8)(1-0.85)=0.003
所以,三科成绩均未获得第一名的概率是0.003。
(2)

=

=[1-P(A)]P(B)P(C)+P(A)[1-P(B)]P(C)+P(A)P(B)[1-P(C)]
=(1-0.9)×0.8×0.85+0.9×(1-0.8)×0.85+0.9×0.8×(1-0.85)
=0.068+0.153+0.108=0.329
所以,恰有一科成绩未获得第一名的概率是0.329。
2. 为考察高中生的数学成绩与语文成绩之间的关系,对高二(1)班的55名学生进行了一次摸底考试,按照考试成绩优秀和不优秀统计成绩后,得到如下表:
| | 优秀 | 不优秀 | 总计 |
| 数学成绩 | 21 | 34 | 55 |
| 语文成绩 | 13 | 42 | 55 |
| 总计 | 34 | 76 | 110 |
问:数学成绩与语文成绩在多大程度上有关系?
假设“数学成绩与语文成绩没有关系”,而随机变量的观测值
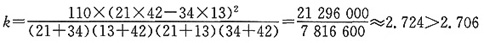
且P(K
2≥2.706)≈0.10
这就意味着“数学成绩与语文成绩没有关系”这一结论是错误的可能性约为0.10,即有90%的把握认为“数学成绩与语文成绩有关系”。
3. 抛掷一颗骰子两次,定义随机变量

(1)试写出随机变量ξ的分布列;
(2)抛掷一颗骰子两次,在第一次掷得向上一面点数是偶数的条件下,求第二次掷得向上一面点数也是偶数的概率。
(1)当第一次向上的面的点数等于第二次向上的面点数时,有6种情况,所以
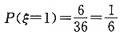
,由互斥事件概率公式得,P(ξ=0)=1-P(ξ=1)=
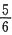
所以所求分布列是
| ξ |
1 |
0 |
| P |
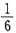 |
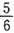 |
|
|
(2)设第一次掷得向上一面点数是偶数的事件为A,第二次掷得向上一面点数是偶数的事件为B,在第一次掷得向上一面点数为偶数的条件下,第二次掷得向上一面点数也是偶数的概率为:
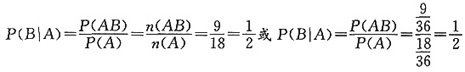
4. 一球赛先分A、B两组,每组各有5球队,第一轮赛后每组的前两名将进入半决赛,为提高上座率,举行有奖竞猜活动(入场券背面设计成选票):首场入场后立即要求观众从两组中各猜2个能进入半决赛的球队,猜中四个队获一等奖,猜中三个队获二等奖,猜中两个队获三等奖,猜中一个队获四等奖,设某人的获奖等级为ξ(当该人未获奖时,记ξ=5),求ξ的数学期望。
ξ可取值为1,2,3,4,5。
ξ的分布列为:
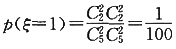
,
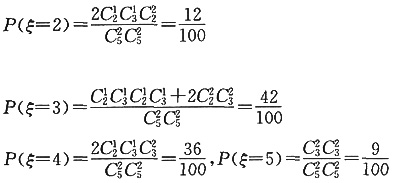
所以这个人获奖等级的期望是:
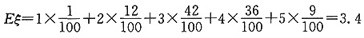
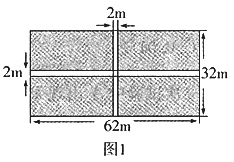
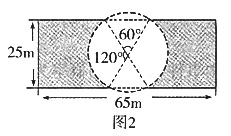
5. 某市为了进一步改善居民的生活环境,同林处决定增加公园A和公园B的绿化面积。已知公园A、B分别有如图1、图2所示的阴影部分需铺设草坪,在甲、乙两地分别有同种草皮1608m
2和1200m
2出售,且售价一样,若园林处向甲、乙两地购买草皮,其路程和运费单价见下表:
| | 公园A | 公园B |
| 路程(千米) | 运算单价(元) | 路程(千米) | 运费单价(元) |
| 甲地 | 30 | 0.25 | 32 | 0.25 |
| 乙地 | 22 | 0.3 | 30 | 0.3 |
(注:运费单价指将每平方米草皮运送1千米所需的人民币)
(1)分别求出公园A、B需铺设草坪的面积;(结果精确到1m
2)
(2)请设计出总运费最省的草皮运送方案,并说明理由。
(1)设公园A、B需铺设草坪的面积分别为S
1、S
2,根据题意,得
S
1=62×32-62×2-32×2+2×2=1800m
2。
设图2中圆的半径为R,由图形知,圆心到矩形较长一边的距离为
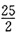
,
所以
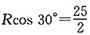
,有
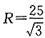
。
于是,
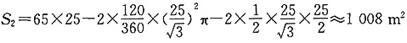
。
所以公园A、B需铺设草坪的面积分别为1800m
2和1008m
2。
(2)设总运费为y元,公园A向甲地购买草皮xm
2,向乙地购买草皮(1800-x)m
2。
由于公园A、B需要购买的草皮面积总数为1800+1008=2808(m
2),
甲、乙两地出售的草皮面积总数为1608+1200=2808(m
2)。
所以,公园B向甲地购买草皮(1608-x)m
2,
向乙地购买草皮1200-(1800-x)=(x-600)(m
2)。
于是,有
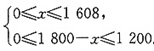
所以600≤x≤1608。又由题意得
y=30×0.25x+22×0.3×(1800-x)+32×0.25×(1608-x)+30×0.3×(x-600)=1.9x+19344
因为函数y=1.9x+19344随x的增大而增大,
所以,当x=600时,有最小值y=1.9×600+19344=20484(元)。
因此,公园A在甲地购买600m
2,在乙地购买1800-600=1200(m
2);
公园B在甲地购买1608-600=1008(m
2)时,运送草皮的总运费最省。
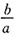 <1;④若a>0,则b-a<b其中正确的有______。
<1;④若a>0,则b-a<b其中正确的有______。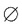 D.{-1}
D.{-1}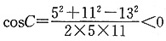 ,所以角C为钝角。故选C。
,所以角C为钝角。故选C。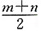 元的价格把笔全部卖给了胜昔,结果他赔了钱,原因是______。
元的价格把笔全部卖给了胜昔,结果他赔了钱,原因是______。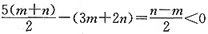 ,所以m>n。故选A。
,所以m>n。故选A。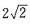 ,则直线l的倾斜角的取值范围是______。
,则直线l的倾斜角的取值范围是______。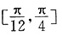 B.
B.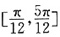
 D.
D.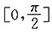
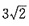 为半径的圆,ax+by=0是一过原点的直线。当圆心到直线距离小于或等于
为半径的圆,ax+by=0是一过原点的直线。当圆心到直线距离小于或等于 时,能够满足题意。设y=kx为直线方程,∴
时,能够满足题意。设y=kx为直线方程,∴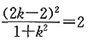
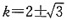 。设倾斜角为β,则
。设倾斜角为β,则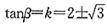 ,解得
,解得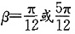 。故选B。
。故选B。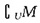 =______。
=______。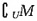 =[0,2]。故选A。
=[0,2]。故选A。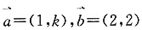 ,且
,且 与
与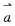 共线,那么
共线,那么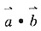 的值为______。
的值为______。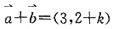 ,∵
,∵ 与
与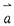 共线,∴3×2-(2+k)×2=0,解得k=1,
共线,∴3×2-(2+k)×2=0,解得k=1,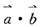 =1×2+1×2=4。故选D。
=1×2+1×2=4。故选D。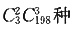


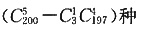
 种,有3种次品的抽法
种,有3种次品的抽法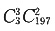 种。故选B。
种。故选B。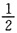 B.
B.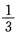
 D.
D.
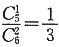 。故选B。
。故选B。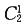 ×0.04×(1-0.04)=0.0768。故选A。
×0.04×(1-0.04)=0.0768。故选A。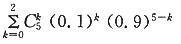
 ·(0.1)2·(0.9)3
·(0.1)2·(0.9)3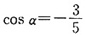 ,且
,且 ,则tanα=______。
,则tanα=______。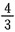
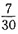
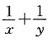 的最小值是______。
的最小值是______。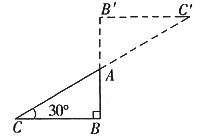
 ,∠CAD=∠CBD=60°,则拉线AC的长是______m。
,∠CAD=∠CBD=60°,则拉线AC的长是______m。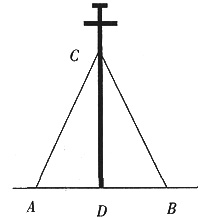
 的值等于______。
的值等于______。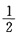



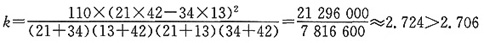

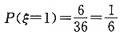 ,由互斥事件概率公式得,P(ξ=0)=1-P(ξ=1)=
,由互斥事件概率公式得,P(ξ=0)=1-P(ξ=1)=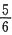
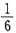
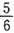
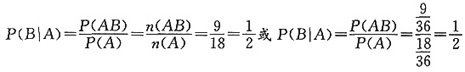
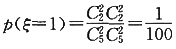 ,
,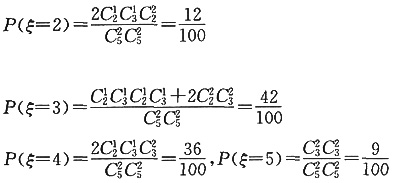
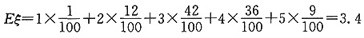
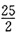 ,
,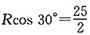 ,有
,有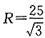 。
。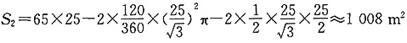 。
。