一、单项选择题在每小题列出的四个备选项中只有一个是符合题目要求的。
2. 设函数

,则f(x)=______
A.x
2 B.x
2-2
C.x
2+2 D.

A B C D
B
[解析]

,∴f(x)=x
2-2.答案为B.
4. 要使函数

在x=0处连续,应给f(0)补充定义的数值是______
A.

B.2
C.1 D.0
A B C D
C
[解析]

,补充定义f(0)=1,则f(x)连续.答案为C.
8. 设∫f(x)dx=F(x)+C,则不定积分∫2
xf(2
x)dx=______
A.

B.F(2
x)+C
C.F(2
x)ln2+C D.2
xF(2
x)+C
A B C D
A
[解析] F(2
x)+C'=∫f(2
x)d(2
x)=∫2
x(ln2)f(2
x)dx=ln2∫2
xf(2
x)dx,所以

.答案为A.
10. 设z=(2x+y)
y,则

=______
A B C D
B
[解析] 由z=(2x+y)
y,则

,

|
(0,1)=2(0+1)
0=2.答案为B.
三、计算题1. 设

求

及

.
在点x=0处,因为f(0+0)=

(2x
2+4)=4,所以

=4.
在点x=2处,f(2+0)=

f(2-0)=

,因为f(2+0)≠f(2-0),所以

不存在.
2. 求曲线y=e
x上的一点(x,y),使过该点的切线与直线y=2x平行.
直线y=2x的斜率为2,曲线y=ex在x处切线的斜率为y'=ex,两直线平行要求它们的斜率相等,即有ex=2,解得x=ln2,代入方程得y=eln2=2.
3. 设

,求f
(n)(0).
f(x)=-ln(1+x),
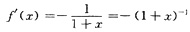
f"(x)=-(-1)(1+x)
-2,
f"'(x)=-(-1)(-2)(1+x)
-3,
……
f
(n)(x)=-(-1)(-2)…(-n+1)(1+x)
-n =

,
故f
(n)(0)=(-1)
n(n-1)!
4. 某商品的需求函数为Q=100-5P,其中Q为需求量,P为价格,求需求的价格弹性函数,并求P=10时的价格弹性.
需求函数表示商品的需求量与价格之间的关系,需求的价格弹性反映需求量的变动对价格变动的敏感程度,设

为需求的价格弹性,则需求的价格弹性函数为:

.当P=10时,

结果说明,当商品的价格在P=10的基础上上升1%时,人们对它的购买量就会下降1%.
5. 求

.
四、综合题某商品的需求函数为Q=180-10P,企业生产该商品的成本函数为C=3Q+0.1Q2.
试求:1. 该商品的总收益函数、平均收益函数
总收益函数为R=QP(Q).
因为Q=180-10P,∴P=

,从而总收益为R=Q·P=Q(18-

)=18Q-

,平均收益函数为

.
2. 该商品的平均成本函数
已知成本函数为C=3Q+0.1Q
2,所以平均函数为

=3+0.1Q.
3. 该商品的总利润函数
总利润=总收益-总成本,所以总利润函数为L=R-C=

Q
2-3Q-0.1Q
2=
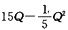
.
4. 当产量为30时的利润
产量为30时,利润为L(30)=15×30-

=270.
5. 某工厂生产某种产品,每批至少生产5(百台),最多生产20(百台),如生产x(百台)的成本C(x)=
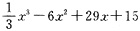
,可得收入R(x)=20x-x
2(万元),问每批生产多少时,可使工厂获得最大利润?
总利润函数为
L(x)=R(x)-C(x)=(20x-x
2)-(

-6x
2+29x+15)

.
令L'(x)=-x
2+10x-9=-(x-1)(x-9)=0,
得驻点x=9,x=1(舍去).
由L"(x)=-2x+10,L"(9)=-8<0,故知当每批生产9百台时利润最大.
6. 求曲线y=x
3-3x+2与它的右极值点处的切线所围成的图形的面积.
y'=3x
2-3,y"=6x.
令y'=0,得x=1,x=-1;y"(1)=6>0,y"(-1)=-6<0,
所以x=-1,x=1是它的极值点,且x=1为右极值点.这时
y'(1)=0,y(1)=1-3+2=0,
故y=0为该曲线在右极值点x=1处的切线方程.
又当y=0时,x=1,x=-2.
因此

.
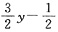 ,且收入为零时的总消费支出C0=70.
,且收入为零时的总消费支出C0=70.
求:7. 消费函数C(y)

.
又∵C(0)=70.∴C(y)=

.
8. 收入由100增到196时消费支出的增量
由

,
故收入由100增加到196时,消费支出增加21264.