二、条件充分性判断解题说明:本大题要求判断所给出的条件能否充分支持题干中陈述的结论.阅读条件(1)和(2)后,选择以下相应的选项.
A:条件(1)充分,但条件(2)不充分.
B:条件(2)充分,但条件(1)不充分.
C:条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.
D:条件(1)充分,条件(2)也充分.
E:条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.
1. 不同的投信方法3
4.
(1)四封信投入3个不同的信箱,其不同的投信方法;
(2)三封信投入4个不同的信箱,其不同的投信方法.
A
条件(1),对于每封信都有3种选择的机会,故为34;条件(2),对于每封信都有4种选择的机会,故为43.
2. 不同的分配方案共有36种.
(1)4名教师分配到3所中学任教,每所中学至少1名教师;
(2)3名教师分配到4所中学任教,每所中学至多1名教师,且教师都必须分出去.
A

.
3. P=0.3.
(1)在五个数字1,2,3,4,5中,若随机取出三个数字,则剩下两个数字都是奇数的概率P:
(2)在五个数字1,2,3,4,5中,若随机取出三个数字,则剩下两个数字都是偶数的概率P.
D
条件(1)显然成立,条件(2)在通常情况下,一个含有三个未知数的方程的解是不确定的,但必须注意题设中p、q、r均为质数这个条件.若p、q均为奇质数,则r必为偶数,且r>2,此时r为合数.这与题设矛盾.因此,p、q必有一个为偶数.注意到既是质数又为偶数的只有2且是最小质数,结合题设条件p<q<r,从而必有p=2.
4. 某组有学生6人,血型分别为:A型2人,B型1人,以及AB型和O型血的人,则随机抽取两人,两人血型相同的概率
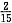
.
(1)AB型血有2人;(2)O型血有1人.
D
由条件(1)得到O型血的人有1人,因此两个人血型相同的概率为
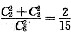
;由条件(2)得到AB型血的人有2人,因此两个人血型相同的概率为

.
5. 一部4卷的文集,按任意次序放到书架上,
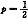
.
(1)p为第一卷不出现在两旁的概率;
(2)p为第一卷与第二卷不相邻的概率.
D
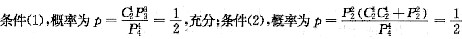
.
6.
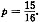
(1)5封信随机投进甲、乙两个空信筒,两个信筒都有信的概率为p;
(2)6个运动队中有两个强队,先任意将6个队分为两组(每组3个队)进行比赛,则这两个强队被分到第一组的概率是p.
A
针对条件(1)而言,按对立事件求解,
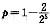
,充分.针对条件(2)而言:两个强队被分到第一组的概率为:
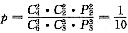
,不充分.
7. 将一颗质地均匀的骰子(它是一种各面上分别标有点数1,2,3,4,5,6的正方体玩具)先后抛掷3次,则
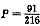
(1)至少出现一次6点向上的概率是P;
(2)6点向上一次都不出现的概率是P.
A

.
8. 掷n次均匀硬币出现正面次数多于出现反面次数的概率
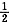
.
(1)n为偶数;(2)n为奇数.
B
设A={正面次数<反面次数),B={正面次数=反面次数},C={正面次数>反面次数}.显然P(A) =P(C),且
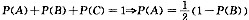
,当n为奇数时,
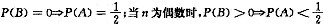
.
9. 口袋内装有10个不同的球,其中5个球标有数字0,5个球标有数字1,若从袋中摸出5个球,那么
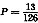
.
(1)摸出的5个球所标数字之和小于2的概率是P;
(2)摸出的5个球所标数字之和大于3的概率P.
10. 某班新年联欢会原定的5个节目已排成节目单,开演前又增加了n个新节目.如果将节目插入原节目单中,那么不同插法的种数为
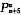
.
(1)n=2;(2)n=3.
D
条件(1)种数有
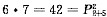
,条件(2)种数有
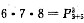
.
11. 有红、白球若干个,可以确定这堆红球、白球共有150个.
(1)若每次拿走一个红球和3个白球,拿到没有红球时,还剩下30个白球;
(2)若每次拿走一个红球和3个白球,则拿到30次时没有红球了.
C
显然条件(1)和条件(2)单独都不能使结论成立.则条件(1)和条件(2)合起来,由条件(2)知道每次拿4个球,30此,共拿了120个球,由条件(1)可知剩下30个球,则共有150个球.
12. 命中率为
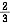
.
(1)一射手对同一目标独立地进行3次射击,已知至少命中一次的概率为
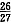
,则此射手的命中率;
(2)一射手对同一目标独立地进行4次射击,已知至少命中一次的概率为
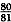
,则此射手的命中率.
D
条件(1),设命中率为p,则有
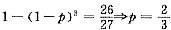
;条件(2),同理可知
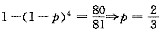
.
13. 不同的选择方案共有240种.
(1)从6人中选出4人分别到巴黎、伦敦、悉尼、莫斯科四个城市游览,要求每个城市有一人游览,每人只游览一个城市;
(2)这6人中甲、乙两人不去巴黎游览.
C
单独显然不行,联立,分三种情况:甲乙两人都去有
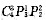
中;甲乙两人去了一个人有
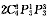
种,甲乙两人都没有去有P
44种,则共有
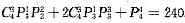
.
14. N=24.
(1)在1,2,3,4,5这五个数字组成的没有重复数字的三位数中,各位数字之和为偶数的共有N个;
(2)在1,2,3,4,5这五个数字组成的没有重复数字的三位数中,各位数字之和为奇数的共有N个.
B

.
15. 已知概率为
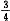
.
(1)从5张100元,3张200元,2张300元的奥运预赛门票中任取3张,则所取3张中至少有2张价格相同的概率;
(2)从5张100元,4张200元,1张300元的奥运预赛门票中任取3张,则所取3张中至少有2张价格相同的概率.
A
条件(1)取3张中至少有2张价格相同的概率的对立事件为3张票都不一样,则答案为
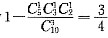
,充分;条件(2)取3张中至少有2张价格相同的概率的对立事件为3张票都不一样,则答案为
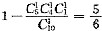
,不充分.
16. 对某批电子产品进行质量检查,每件检查后放回,在连续检查三次时至少有一次是次品的概率是0.271.
(1)该产品的合格率是0.8;
(2)该产品的次品率是0.1.
B
设其合格率为p,考虑其反面,反面应当是没有次品,故至少有一次次品的概率是1-p3=0.271,即p=0.9,显然只有条件(2)充分,选B.
17. (1)五人站成一列,重新站队时,各人都不站在原来的位置上;
(2)五人站成一列,甲不站在正中间.
A
条件(1),设原来站在第i个位置的人是a
i(i=1,2,3,4,5).重新站队时,a
1站在第2个位置的站法有P
44种,其中不符合要求的有:a
3站第3位的P
33种,a
4站第4位的P
33种,但有的站法在考虑a
3的情形时已经减去了,故只应再算
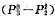
种,同理,a
5站第5位的应再算
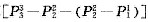
种.a
1站在第3,4,5位的情形与站在第2位的情形是对等的,故所有符合要求的站法有:
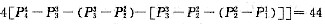
种,充分;条件(2),
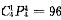
,不充分.
18.
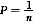
.
(1)在编号为1,2,3,…,n的n张奖卷中,采取不放回方式抽奖,若1号为获奖号码,则在第k次(l≤k≤n)抽签时抽到1号奖卷的概率;
(2)在编号为1,2,3,…,n的n张奖卷中,采取要放回方式抽奖,若1号为获奖号码,则在第k次(l≤k≤n)抽签时抽到1号奖卷的概率.
D
条件(1),只要从n-1张奖券中抽取的前k-1张都不中即可,故概率为

,充分;条件(2),显然其概率为
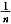
,亦充分·
19. 已知概率为
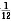
.
(1)将一骰子连续抛掷四次,它落地时向上的点数依次成等差数列的概率;
(2)将一骰子连续抛掷三次.它落地时向上的点数依次成等差数列的概率.
B
条件(1)成等差数列的是{1,1,1,1},…,{6,6,6,6},{1,2,3,4),{4,3,2,1},{2,3,4,5),{5,4,3,2),{3,4,5,6),{6,5,4,3)共12种,概率为
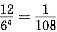
,不充分;条件(2),同理,概率为
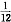
充分.
20. N=28.
(1)满足m,n∈N
*且m+n<8,则平面上的点(m,n)共有N个;
(2)满足m,n∈N
*且m+n≤8,则平面上的点(m,n)共有N个.
E
(1)取m=0,则n可以取0,1,…,6,7这8个点,取m=1,则n可以取0,1,…,6这7个点,依次类推知道共有36个点满足条件;条件(2),取m=0,则n可以取0,1,…,7,8这9个点,取m=1,则n可以取0,1,…,6,7这8个点,依次类推知道共有45个点满足条件.
21. 用四种颜色对下列各图的A,B,C,D,E五个区域染色,要求相邻的区域染不同的颜色.则共有72种不同染法.
(1)图形如图2.6.3(a)所示; (2)图形如图2.6.3(b)所示.

B
由条件(1),按照A,B,C,D,E依次染色,可供选择的颜色依次为4,3,2,2,2种.由条件(2),按照A,B,E,C,D依次染色,分两类,当B与E同色时有4×3×1×2×2=48种,当B与E不同色时有4×3×2×1×1=24种.
22. 在一小时内至多2台机床需要工人照看的概率是0.9728;
(1)一台X型号自动机床在一小时内不需要工人照看的概率为0.8;
(2)有四台这中型号的自动机床各自独立工作.
C
显然两条件单独均不充分,考虑联合,则有
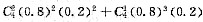
+(0.8)4=0.9728,充分.
23. 72不是6的倍数.
(1)n不是3的倍数;(2)n不是2的倍数.
24. 可确定某射击选手一次射击的命中率是2/3.
(1)一名射击选手向目标连续射击4次,至少命中一次的概率是80/81;
(2)一名射击选手向目标连续射击3次,只有第二次未命中的概率为2/27.
A
针对条件(1)而言,设定命中一次的概率为P,则根据题意可知:1-(1-P)
3=
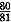
,所以P=2/3,充分;针对条件(2)而言,根据题意可知:
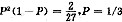
,不充分.
25.
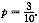
(1)甲、乙、丙、丁、戊5人站成一排,则甲、乙相邻,甲、丙不相邻的概率为p;
(2)甲、乙、丙、丁、戊5人站成一排,则甲、乙、丙3个人连在一起的概率为p.
D
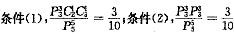
.
26.
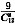
.
(1)停车场可把12辆车停放在一排上,当有9辆车已停放后而恰有3个空位连在一起,这样的事件发生的概率;
(2)停车场可把12辆车停放在一排上,当有8辆车已停放后而恰有4个空位连在一起,这样的事件发生的概率.
B
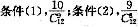
.
27. 一批零件共100个,其中有95件合格品,5件次品,每次任取1个零件装配机器,则P
2=P
3.
(1)第2次取到合格品的概率是P
2;
(2)第3次取到合格品的概率是P
3.
C
显然单独的两条件均不充分,考虑联合.
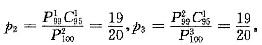
,充分.
28.
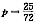
.
(1)有放回的取棋子.棋子有i种颜色,5颗红色,4颗黄色,3颗白色.两次都取到同一种颜色的概率p.
(2)不放回的取棋子.棋子有三种颜色,5颗红色,4颗黄色,3颗白色.两次都取到同一种颜色的概率p.
A
由条件(1),每颗棋子的概率如表2.5.1所示.

因此两次取出棋子,同色分三个情况,红红,黄黄,白白.所以概率为
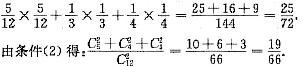
29. 若以连续掷两次骰子分别得到的点数m、n作为点Q的坐标,则
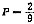
.
(1)点Q落在圆x
2+y
2=9内的概率是P;
(2)点Q落在圆x
2+y
2=16内的概率是P.
B
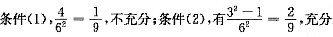
.
30.
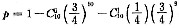
.
(1)甲每次投篮命中率为
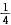
,投10次,中2次的概率为p;
(2)甲每次投篮命中率为
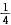
,投10次,中2次以上的概率为p.
B
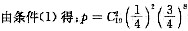
;
由条件(2)得:
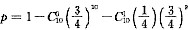
.
31. N=144.
(1)四个不同的小球放入编号为1,2,3,4的四个盒中恰有一个空盒的放法为N种.
(2)四个不同的小球放入编号为1,2,3,4的四个盒中恰有一个盒中放两个小球的放法为N种.
D
两个条件等价,则
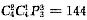
.
32. 至少有两人生日在同一天的概率
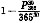
(1)某班30名同学,一年按365天计算,至少有两人生日在同一天的概率,
(2)某班30名同学,一年按365天计算,恰有两人生日在同一天的概率.
A
条件(1),没有两个同学在同一天出生为
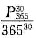
,则至少有两人生日在同一天的概率为
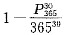
;条件(2),恰有两人生日在同一天的概率为
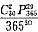
.
33. 从1,2,…,9这九个数中,随机抽取N个不同的数,则这N个数的和为偶数的概率是
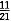
.
(1)N=2;(2)N=3.
B
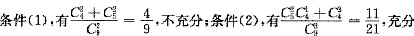
.
34. 在一个小组中有8名女同学和4名男同学,从中任意地挑选N名同学担任交通安全宣传志愿者,那么选到的N名都是女同学的概率是
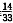
.
(1)N=3;(2)N=2.
B
条件(1),有

,不充分;条件(2),有
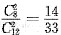
,充分.
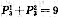 种,同理以2,3,4结尾的三位数各有9种,则选出的三位数的个位数字之和为9×(1+2+3+4)=90.
种,同理以2,3,4结尾的三位数各有9种,则选出的三位数的个位数字之和为9×(1+2+3+4)=90.
 ;另一种,有两个点在AB上,但考虑到不与第一种重复,交点除外,故有
;另一种,有两个点在AB上,但考虑到不与第一种重复,交点除外,故有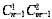 ,从而共有
,从而共有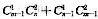 .
.
 .
.
 .
. .
.
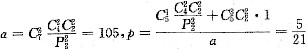 .
. .
. .
.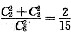 ;由条件(2)得到AB型血的人有2人,因此两个人血型相同的概率为
;由条件(2)得到AB型血的人有2人,因此两个人血型相同的概率为 .
.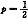 .
.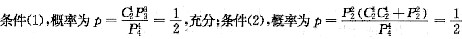 .
.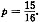
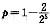 ,充分.针对条件(2)而言:两个强队被分到第一组的概率为:
,充分.针对条件(2)而言:两个强队被分到第一组的概率为: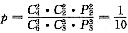 ,不充分.
,不充分.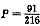
 .
.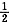 .
.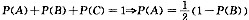 ,当n为奇数时,
,当n为奇数时,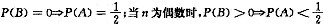 .
.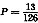 .
.
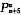 .
.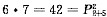 ,条件(2)种数有
,条件(2)种数有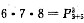 .
.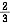 .
.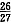 ,则此射手的命中率;
,则此射手的命中率;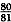 ,则此射手的命中率.
,则此射手的命中率.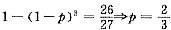 ;条件(2),同理可知
;条件(2),同理可知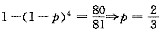 .
.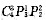 中;甲乙两人去了一个人有
中;甲乙两人去了一个人有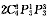 种,甲乙两人都没有去有P44种,则共有
种,甲乙两人都没有去有P44种,则共有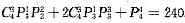 .
. .
.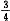 .
.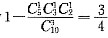 ,充分;条件(2)取3张中至少有2张价格相同的概率的对立事件为3张票都不一样,则答案为
,充分;条件(2)取3张中至少有2张价格相同的概率的对立事件为3张票都不一样,则答案为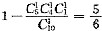 ,不充分.
,不充分.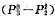 种,同理,a5站第5位的应再算
种,同理,a5站第5位的应再算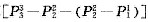 种.a1站在第3,4,5位的情形与站在第2位的情形是对等的,故所有符合要求的站法有:
种.a1站在第3,4,5位的情形与站在第2位的情形是对等的,故所有符合要求的站法有: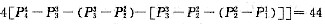 种,充分;条件(2),
种,充分;条件(2),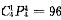 ,不充分.
,不充分.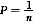 .
. ,充分;条件(2),显然其概率为
,充分;条件(2),显然其概率为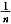 ,亦充分·
,亦充分·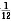 .
.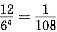 ,不充分;条件(2),同理,概率为
,不充分;条件(2),同理,概率为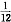 充分.
充分.
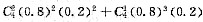 +(0.8)4=0.9728,充分.
+(0.8)4=0.9728,充分.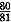 ,所以P=2/3,充分;针对条件(2)而言,根据题意可知:
,所以P=2/3,充分;针对条件(2)而言,根据题意可知: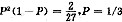 ,不充分.
,不充分.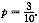
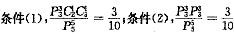 .
.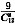 .
.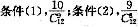 .
.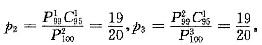 ,充分.
,充分.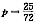 .
.
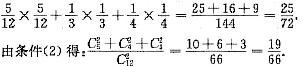
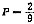 .
.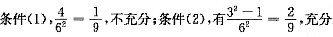 .
.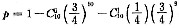 .
.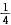 ,投10次,中2次的概率为p;
,投10次,中2次的概率为p;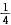 ,投10次,中2次以上的概率为p.
,投10次,中2次以上的概率为p.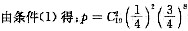 ;
;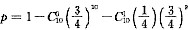 .
.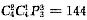 .
.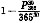
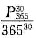 ,则至少有两人生日在同一天的概率为
,则至少有两人生日在同一天的概率为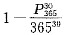 ;条件(2),恰有两人生日在同一天的概率为
;条件(2),恰有两人生日在同一天的概率为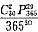 .
.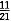 .
.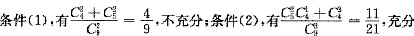 .
.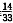 .
. ,不充分;条件(2),有
,不充分;条件(2),有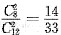 ,充分.
,充分.