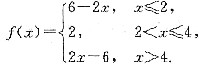A.条件(1)充分,但条件(2)不充分.
B.条件(2)充分,但条件(1)不充分.
C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.
D.条件(1)充分,条件(2)也充分.
E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.1. 今年哥哥和弟弟年龄的几何平均值为
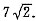
(1)哥哥和弟弟三年后的年龄和为27;
(2)今年弟弟年龄恰是兄弟两人年龄的差.
(C).
[解析] 设哥哥年龄为z,弟弟年龄为Y,条件(1)中,令x=20,y=1,它们几何平均

它们的几何平均值为
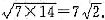
即条件(1)、条件(2)联合起来充分.故选(C).
2. 某厂2003年6月份产值是1月份产值的a倍.
(1)2003年上半年,该厂月产值的平均增长率为
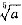
;
(2)2003年上半年,该厂月产值的平均增长率为
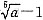
.
(E).
[解析] 条件(1)中,设k月份产值为a
k(1≤k≤6,k∈N),{a
k}是公比
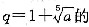
等比数列,则
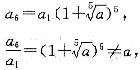

3. a:b=5:3.
(1)甲、乙两人走同样的距离,甲、乙速度分别为a,6,它们所用的时间之比为3:5;
(2)甲、乙两座水库,库存水量分别为a,6,若将甲水库存水的20%输入乙水库,则两水库的存水量相等.
(D) 。
[解析] 条件(1)中,设甲、乙所用的时间分别为3k和5k(k>0).由题意,有
3ka=5kb.
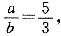
条件(1)充分.条件(2)中,甲水库输入乙水库20%后存水量为(1-20%)a=
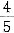
a,乙水库后来水量为b+
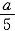
,由题意
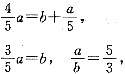
条件(2)也充分,故选(D).
4. 存在实数m的值,使|m+2|+|6-3m|≤a成立.
(1)a=2; (2)a>4.
(B).
[解析] |m+2|+3|m-2|≤a,令f(x)=|x+2|+3|x-2|,零点x=±2,分段考虑.
(1)x<-2时,f(x)=-(x+2)-3(x-2)=-4x+4;
(2)-2≤x≤2时,f(x)=x+2-3(x-2)=-2x+8;
(3)x>2时,f(x)=(x+2)+3(x-2)=4x-4.
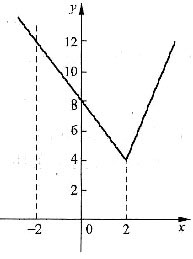
函数y=f(x)图像如图1-10所示,由图可知f(x)≤a有解的条件为n≥4.因此,当且仅当a≥4时,存在有m∈R,使得|m+2|+|6-3m|≤a成立.条件(1)不充分,条件(2)充分,故选(B).
5. x
2-3z-18>0.
(1)|2x-3|=|x+3|+|x-6|; (2)x
2-2x-15>0.
(E).
[解析] x2-3x-18>0的解为x<-3或x>6.条件(1)中
|2x-3|=|(x+3)+(x-6)|=|x+3|+|x-6|,(x+3)(x-6)≥0,从而x≤-3或x≥6.条件(1)不充分.条件(2)中,x2-2x-15>0,x<-3或x>5,条件(2)也不充分,故选(E).
6. x
2-2x<0.
(1)三个实数1,2-x,x的几何平均值比它们的算术平均值要小;
(2)x
2-5x+6>0.
(A).
[解析] x
2-2x<0,0<x<2.条件(1)中,
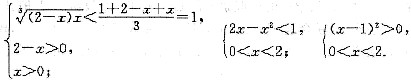
因而0<x<1或1<x<2,条件(1)充分.条件(2)中,x<2或x>3,条件(2)不充分.故选(A).
7. x+y=20.
(1)x:y=2:3; (2)(x+10):(y+10)=9:11.
(C).
[解析] 条件(1)中,令x=2,y=3,x+y=5≠20,条件(1)不充分.条件(2)中,令x=-1,y=1,x+y=0≠20,条件(2)不充分,将条件(1)、条件(2)联合起来,
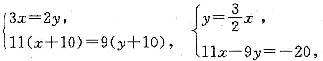
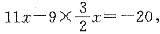
-5x=-40,x=8,y=12.
x+y=20.即条件(1)、条件(2)联合起来充分.故选(C).
8. 可以确定
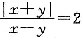
.
(1)
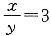
; (2)
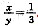
.
(E).
[解析] 条件(1)中,令x=-3,y=-1,则
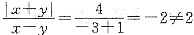
,条件(1)不充分.条件(2)中,令x=1,y=3,则
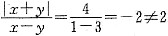
,条件(2)也不充分.条件(1)、条件(2)彼此矛盾,无法联合,故选(E).
9. 甲、乙两个水产品仓库,欲使它们的储存量相等,甲仓库需向乙仓库调运的水产品占甲仓库原库存量的15%.
(1)现库存水产品之比为
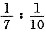
;
(2)甲仓库现有水产品可供宾馆20天用,乙仓库现有水产品可供该宾馆14天用。
(D).
[解析] 条件(1)中,
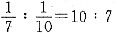
,甲仓库比乙仓库多的部分占甲仓库的30%,要使两仓库库存相等,甲仓库需乙仓库调运的水产品占甲仓库原库存量的
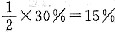
,条件(1)充分.条件(2)中,甲仓库与乙仓库库存量之比为20:14=10:7,同条件(1).因此,条件(2)也充分.故选(D).
10. 2007年底某市房价与2006年初持平,2006年涨价达25%.
(1)2007年该市房价下调25%;
(2)2007年该市房价下调20%.
(B).
[解析] 设2006年初房价为a,2006年房价增长率为x.条件(1)中,
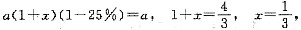
条件(1)不充分,条件(2)中,
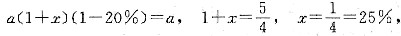
条件(2)充分.故选(B).
11. 百信鞋店卖的意大利皮鞋价格下降了60%.
(1)原来买两双鞋的钱,现在可以买五双;
(2)原来的价格是现在价格的2.5倍.
(D).
[解析] 条件(1)中,设z是原来买两双鞋的钱,则皮鞋价格下降了
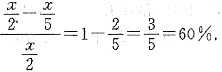
从而条件(1)充分.条件(2)中,设y是现在价格,原来价格为2.5y,则皮鞋价格下降了
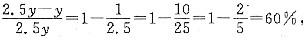
条件(2)也充分.故选(D).
12. x,y∈R,则|x|+|y|=|x-y|.
(1)x>0,y<0; (2)-x<0,y>0.
(D).
[解析] |x-y|=|x+(-y)|=|x|+|-y|,从而x(-y)≥0,xy≤0.从而条件(1)、条件(2)单独都充分.故选(D).
13. 某人投资股市,用3万元买进A,B各若干股,他在交易中的收益是1500元.
(1)买A,B股之比是3:2;
(2)当A股升值15%,B股下跌10%时全部抛出.
(C).
[解析] 条件(1)没给抛时的股票升降幅度,条件(2)没给A,B股比例,因而单独都不充分,将条件(1)、条件(2)联合起来考虑,由条件(1)知A股买了1.8万元,B股买了1.2万元,再由条件(2),有1.8×0.15-1.2×0.10=0.15(万元)=1500(元).即联合起来充分.故选(C).
14. 方程|x+1|+|x|=2无根.
(1)x∈(-∞,-1); (2)x∈(-1,1).
(B).
[解析] 设f(x)=|x+1|+|x|,由绝对值的几何意义,f(x)的最小值为1,当-1≤x≤0时,f(x)取得最小值,从而条件(2)充分.而在条件(1)中,令
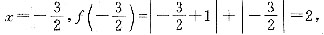
因而条件(1)不充分.故选(B).
15. 一个容器中盛有纯盐酸x L,第一次倒出4 L以后,用水加满,第二次倒出4 L后,再用水加满.则容器中盐酸的浓度是36%.
(1)x=10; (2)x=15.
(A).
[解析] 设原来装有纯盐酸x L;由题意,第一次倒后,纯盐酸剩(x-4)L,浓度为
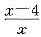
,第二次倒后,纯盐酸剩

。因而有
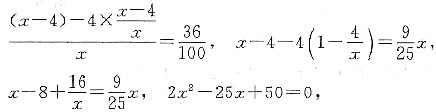
上面方程解得x=10,x=
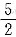
(舍).故选(A) .
16. 一满杯酒的容积

(1)瓶中有
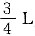
酒,再倒入1满杯酒可使瓶中的酒精增至
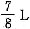
;
(2)瓶中有
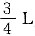
酒,再从瓶中倒出2满杯酒可使瓶中的酒减至
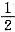
L.
(D).
[解析] 设一满杯酒容积为x L.条件(1)中条件(1)充分.条件(2)中,

,条件(2)也充分.故选(D).
17. 某厂一月份每件产品销售的利润是出厂价的25%,二月份成本不变,则二月份的销售总利润比一月份的销售总利润增长8 9/6.
(1)二月份每件产品的出厂价比一月份降低10%;
(2)二月份销售件数比一月份增加80%.
(C).
[解析] 条件(1)不含销售件数变化,条件(2)不含出厂价的变化,因而条件(1)、条件(2)单独都不充分.将条件(1)、条件(2)联合起来考虑,设每件产品的成本为6,一月份出厂价为a,则由条件(1)可知二月份出厂价为
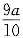
,又设一月份销售件数为c,则由条件(2)可知二月份销售件数为
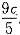
.一月份每件利润
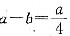
,有b=
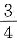
a,一月份总利润为

。
二月份每件利润
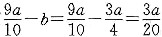
,二月份销售总利润为
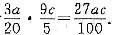
因而,销售总利润二月份比一月份增长
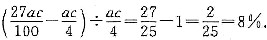
故条件(1)、条件(2)联合起来充分,故选(C).
18. 某厂有两个工程项目,甲项目140人,2006年实现人均利税1.2万元,乙项目有60人,2006年实现人均利税1.5万元,则该厂2007年的人均利税比2006年增加9.3%.
(1)2007年甲项目较2006年人均利税增加10%;
(2)2007年乙项目较2006年人均利税增加8%.
(C).
[解析] 条件(1)无乙项目人均利税增长率,条件(2)无甲项目人均利税增长率,因此条件(1)、条件(2)单独都不充分.将条件(1)、条件(2)联合起来考虑:2006年甲项目总利税140×1.2(万元),乙项目总利税60×1.5(万元),2006年全厂总利税为140×1.2+60×1.5(万元),人均利税
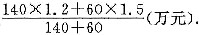
2007年由条件(1)知甲项目总利税140×1.2×1.1(万元),由条件(2)知乙项目总利税60×1.5×1.08(万元),2007年全厂人均利税为
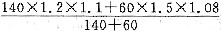
(万元).因此,该厂2007年比2006年人均利税增长率为
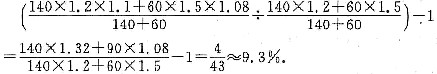
因此,条件(1)、条件(2)联合起来充分.故选(C).
19. 某班学生中,男生比女生人数少.
(1)女生中学习优秀的人数是全班人数的51%;
(2)男生中团员人数是全班人数的48%.
(A).
[解析] 条件(1)中,女生人数≥女生中学习优秀人数>男生人数.从而条件(1)充分.条件(2)中,若男生全部是团员,则男生人数少于女生人数,若男生有50%是团员,则男生人数多于女生人数,条件(2)不充分,故选(A).
20. 1 kg鸡肉的价格高于1 kg牛肉的价格.
(1)一家超市出售袋装鸡肉与袋装牛肉,一袋鸡肉的价格比一袋牛肉的价格高30%;
(2)一家超市出售袋装鸡肉与袋装牛肉,一袋鸡肉比一袋牛肉重25%.
(C).
[解析] 条件(1)中无重量比,条件(2)中无价格比,单独都不充分.将条件(1)、条件(2)联合起来考虑,设牛肉价格一袋为a,牛肉一袋重量为b,则鸡肉一袋价格为(1+30%)a(由条件(1)),鸡肉每袋重(1+25%)b(由条件(2)).牛肉每公斤价格
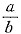
,鸡肉每公斤价格
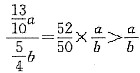
。条件(1)、条件(2)联合起来充分.故选(C).
21. 某工厂的一种产品原来利润率(利润/成本)为32%,由于原材料和石油涨价,成本提高,而按物价局要求出厂价不变,则利润降为20%.
(1)成本提高了20%; (2)成本提高了10%.
(B).
[解析] 设成本提高了32(百分数),出厂价为6,原来成本为a,则后来成本为(1+x)a.原来利润为b-a,利润率为
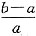
=32%,有b=1.32a;现在利润为b-(1+x)a,利润率为
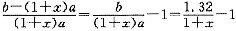
.由利润率降为20%,有
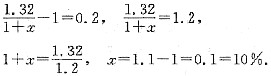
因而,条件(2)充分,条件(1)不充分.故选(B).
22. 甲乙两个工厂生产同一种产品,甲厂今年的产量比去年增加了10%,则乙厂今年产量比去年增加了5.6%.
(1)去年甲厂的产量比乙厂多20%;
(2)今年乙厂的产量比甲厂少20%.
(C).
[解析] 条件(1)中无今年两厂的产量关系,条件(2)中无去年两厂的产量关系,从而条件(1)、条件(2)单独都不充分.将条件(1)、条件(2)联合起来,设去年乙厂产量为a,由条件

条件(1)、条件(2)联合起来充分,故选(C).
23. 不等式1≤|3-2x|<3成立.
(1)0<x<1; (2)2≤x<3.
(D).
[解析] 1≤|2x-3|<3,由绝对值的几何意义有

从而条件(1)、条件(2)单独都充分.故选(D).
24. 某超市近3个月内猪肉涨价两次,使得肉价比原来涨了50%.
(1)第一次涨了20%,第二次涨了30%;
(2)第一次涨了25%,第二次涨了20%.
(B).
[解析] 条件(1)中,设猪肉原价为a,第一次涨价后的价格为(1+20%)a=
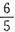
a,第

25. |3x-2|-|3x-7|=5.

(E).
[解析] 条件(1)中,2≤3x≤7,|3x-2|-|3x-7|=3x-2+3x-7=6x-9,条件(1)不充分,条件(2)中,
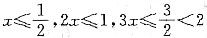
,|3x-2|-|3x-7|=2-3x+3x-7=-5,条件(2)也不充分.故选(E).
26. 某种中成药经过前后两次降价后,比原来的价格下降了36%.
(1)两次各降了18%; (2)两次各降了20%.
(B).
[解析] 设原药价为a.
条件(1)中,两次降价比原来价格下降了

,条件(1)不充分.
条件(2)中,两次降价比原来价格下降了
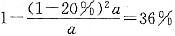
,即条件(2)充分.故选(B).
27. 桶中原有2 kg浓度为30%的酒精.
(1)桶中加入1 kg水,溶液浓度稀释为20%;
(2)桶中加入2 kg水,溶液浓度稀释为15%.
(C).
[解析] 设桶中原来x kg酒精溶液浓度为y(百分数).两个未知数需两个条件,因此,条件(1)、条件(2)单独都不充分.联合条件(1)、条件(2),由条件(1)有
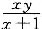
=20%,由条件
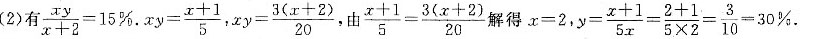
,从而条件(1)、条件(2)联合起来充分.故选(C).
28. 某中学现在有学生1500人,一年后学生将增加54人,则该校现在有男生900人.
(1)计划一年后女生增加3%;
(2)计划一年后男生增加4%.
(C).
[解析] 设现有男生x人,则现有女生(1500-x)人,条件(1)中无男生变化率,条件(2)中无女生变化率.从而单独都不充分,将条件(1)、条件(2)联合起来考虑,则有
(1+3%)(1500-x)+(1+4%)=1500+54,
1.03(1500-x)+1.04x=1554.
解得x=900.从而条件(1)、条件(2)联合起来充分.故选(C).
29. 某人购进一定数量的某股票后,等该股价下跌时,又购进了3倍数量的股票,则当股票的股价反弹到第一次购进股价的92.5%时,全部抛出该股票恰好不赢不亏.
(1)股票价格下跌10%时,购进了3倍数量的股票;
(2)股票价格下跌20%时,购进了3倍数量的股票.
(A).
[解析] 设原来购进该股票数量为x股,股价为每股y元,反弹到第一次购股价的t时抛出.在条件(1)中,第二次购进了3x股,股价为每股0.9y元.第三次以每股价ty元抛出4x股,从而有
3x(t-0.9)y=x(1-t)y,3t-2.7=1-t,
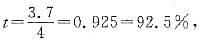
条件(1)充分.条件(2)中,同上有
3x(t-0.8)y=x(1-t)y,3t-2.4=1-t,
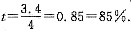
条件(2)不充分.故选(A).
30. 方程|x-7|-|x+a|=10有无数个解.
(1)a=-3; (2)a=3.
(B).
[解析] 条件(1)中,|x-7|-|x-3|=10,当x>7时,|x-7|-|x-3|<0;当3≤x≤7,|x-7|-|x-3|≤4;当x<3时,|x-7|-|x-3|=4,即|x-7|-|x-3|最大值为4,方程|x-7|-|x-3|=10无解,条件(1)不充分.条件(2)中,|x-7|-|x+3|=10,当x≤-3时成立,从而条件(2)充分.故选(B).
31. |x-y|≤5.
(1)|x+3|≤2,|y+3|≤3; (2)|x-3|≤1,|y-3|≤4.
(D).
[解析] 由|x-y|-|(x+a)-(y+a)|≤|x+a|+|y+a|知条件(1)、条件(2)单独都充分,故选(D).
32. 某次MBA数学考试中,在考生中达到或超过“通过分数线”的平均成绩比“通过分数线”高15分;未达“通过分数线”的考生平均成绩比“通过分数线”低25分,全体考生的平均成绩为50分.则“通过分数线”为65分.
(1)40%的考生达到或超过“通过分数线”;
(2)25%的考生达到或超过“通过分数线”.
(B).
[解析] 设考生共有x人,“通过分数线”为y人.由题目大前提可得,在条件(1)中有
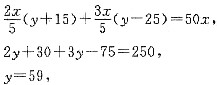
条件(1)不充分.条件(2)中有
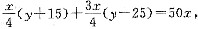
y+15+3y-75=200,
y=65,
条件(2)充分,故选(B).
33. 英语考试全班平均分可求.
(1)16名男生的英语考试总分是1263分,12名女生的英语考试总分是1137分,全班共28人;
(2)男生的英语平均成绩为76.4分,女生英语平均成绩为86.6分.
34. 已知|a|=5,|b|=7,则|a+b|=2.
(1)ab<0; (2)ab>0.
35. 三八国际妇女节,女职工可领到一张美容卡或一个镶金提包,可知公司中领到美容卡的女职工有多少人.
(1)有40%的人领到镶金提包;
(2)美容卡和镶金提包共200份.
36. 学生军训结束后,旅行社用大客车送学生回家,在前门有一部分学生下车,这时车上女生与男生人数之比为1:12.
(1)原来车上女生与男生人数之比为1:3;
(2)车开到前门,女生有
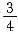
下车,男生无人下车.
37. 某高中班学生中,
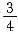
的女生和
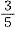
的男生都是共青团员,则该班女生人数与男生人数之比为2:3.
(1)女生团员人数:男生团员人数=5:4;
(2)女生团员人数:男生团员人数=5:6.
(B).
[解析] 设该班有女生x人,男生y人,则该班女生团员人数为
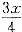
,男生团员人数为

38. 设通往美国的长途电话计费,通话后花了3美元,则它实际通话时间是11 min.
(1)计费标准是3 min内1美元,3 min后每分钟0.25美元;
(2)计费标准是3 min内1.5美元,3 min后每分钟0.2美元.
(A).
[解析] 在条件(1)中,设3分钟后的通话时间是t分钟,则有t×0.25=3-1,t=8,其通话8+3=11(分),条件(1)充分.在条件(2)中,t如前所设,则有t×0.2=3-1.5,t=7.5,共通话7.5+3=10.5(分),条件(2)不充分.故选(A).
39. 一项议案由教职工代表大会投票表决,其中职员占职代会代表的20%,其余均为教师,已知职员对该议案投的全是反对票,则教师投的票中反对票占50%.
(1)总投票数中反对票占70%;
(2)总投票数中反对票占60%.
40. 申请驾驶执照时,必须参加理论考试和路考,且两种考试都要通过,若在同一批学员中有70%的人通过了理论考试,80%的人通过了路考,则最后领到驾驶执照的人有60%.
(1)10%的人两种考试都没有通过;
(2)20%的人仅通过了路考.
(D).
[解析] 设通过理论考试的申请者为集合A,通过路考的申请者为集合B,领到驾驶执照的申请者占的百分数为x.

(70%-x)+x+(80%-x)=90%,
解得x=60%,条件(1)充分.
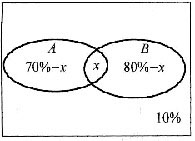
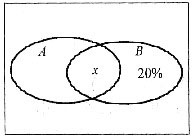
条件(2)中,如图1-12所示,x=80%-20%=60%.条件(2)也充分,故选(D).
41. 不等式|x+2|+|4-x|<S无解.
(1)S≤2; (2)S>2.
(A).
[解析] 令f(x)=|x-2|+|4-x|,由绝对值的几何意义知,f(x)=|x-2|+|x-4|的最小值为2,实际上,
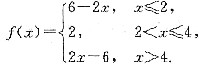
因此,f(x)<S无解的条件是S≤2,条件(1)充分,条件(2)不充分.故选(A).
42. 某人以a元的单价,买入某种股票6股,两天后该股上涨了15%,第三天这只股票却回调了5%,临收市时他将手中的6股全部抛出,则他比前一日卖出少获得利润占他实际获得利润的62%.
(1)a=10,b=1500; (2)a=9,b=2000
43. a、b、c、d∈N
+,且d<1000,a
5=b
4,c
3=d
2,则d-b=100.
(1)a-c=32; (2)a-c=17.
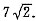

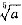 ;
;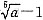 .
.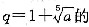 等比数列,则
等比数列,则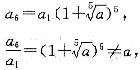

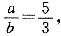
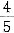 a,乙水库后来水量为b+
a,乙水库后来水量为b+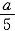 ,由题意
,由题意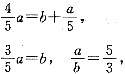

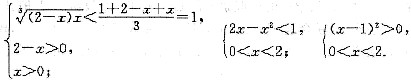
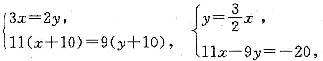
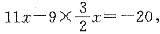 -5x=-40,x=8,y=12.
-5x=-40,x=8,y=12.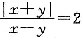 .
.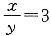 ; (2)
; (2)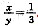 .
.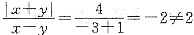 ,条件(1)不充分.条件(2)中,令x=1,y=3,则
,条件(1)不充分.条件(2)中,令x=1,y=3,则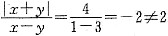 ,条件(2)也不充分.条件(1)、条件(2)彼此矛盾,无法联合,故选(E).
,条件(2)也不充分.条件(1)、条件(2)彼此矛盾,无法联合,故选(E).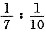 ;
;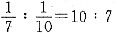 ,甲仓库比乙仓库多的部分占甲仓库的30%,要使两仓库库存相等,甲仓库需乙仓库调运的水产品占甲仓库原库存量的
,甲仓库比乙仓库多的部分占甲仓库的30%,要使两仓库库存相等,甲仓库需乙仓库调运的水产品占甲仓库原库存量的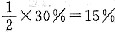 ,条件(1)充分.条件(2)中,甲仓库与乙仓库库存量之比为20:14=10:7,同条件(1).因此,条件(2)也充分.故选(D).
,条件(1)充分.条件(2)中,甲仓库与乙仓库库存量之比为20:14=10:7,同条件(1).因此,条件(2)也充分.故选(D).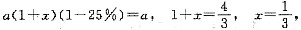
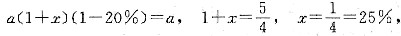
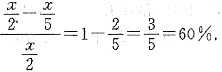
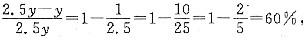
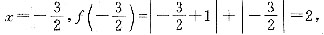 因而条件(1)不充分.故选(B).
因而条件(1)不充分.故选(B).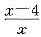 ,第二次倒后,纯盐酸剩
,第二次倒后,纯盐酸剩 。因而有
。因而有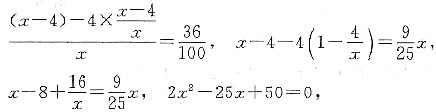
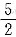 (舍).故选(A) .
(舍).故选(A) .
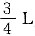 酒,再倒入1满杯酒可使瓶中的酒精增至
酒,再倒入1满杯酒可使瓶中的酒精增至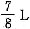 ;
;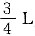 酒,再从瓶中倒出2满杯酒可使瓶中的酒减至
酒,再从瓶中倒出2满杯酒可使瓶中的酒减至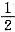 L.
L. ,条件(2)也充分.故选(D).
,条件(2)也充分.故选(D).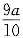 ,又设一月份销售件数为c,则由条件(2)可知二月份销售件数为
,又设一月份销售件数为c,则由条件(2)可知二月份销售件数为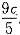 .一月份每件利润
.一月份每件利润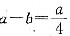 ,有b=
,有b=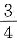 a,一月份总利润为
a,一月份总利润为 。
。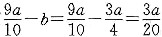 ,二月份销售总利润为
,二月份销售总利润为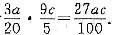
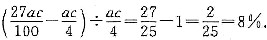
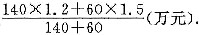
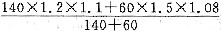 (万元).因此,该厂2007年比2006年人均利税增长率为
(万元).因此,该厂2007年比2006年人均利税增长率为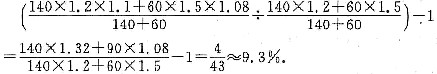
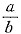 ,鸡肉每公斤价格
,鸡肉每公斤价格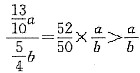 。条件(1)、条件(2)联合起来充分.故选(C).
。条件(1)、条件(2)联合起来充分.故选(C).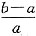 =32%,有b=1.32a;现在利润为b-(1+x)a,利润率为
=32%,有b=1.32a;现在利润为b-(1+x)a,利润率为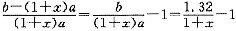 .由利润率降为20%,有
.由利润率降为20%,有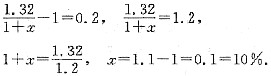


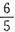 a,第
a,第

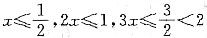 ,|3x-2|-|3x-7|=2-3x+3x-7=-5,条件(2)也不充分.故选(E).
,|3x-2|-|3x-7|=2-3x+3x-7=-5,条件(2)也不充分.故选(E). ,条件(1)不充分.
,条件(1)不充分.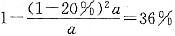 ,即条件(2)充分.故选(B).
,即条件(2)充分.故选(B).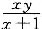 =20%,由条件
=20%,由条件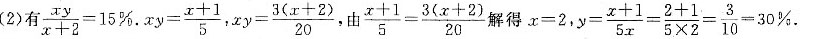 ,从而条件(1)、条件(2)联合起来充分.故选(C).
,从而条件(1)、条件(2)联合起来充分.故选(C).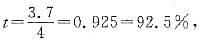
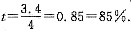
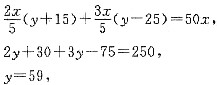
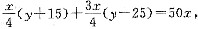
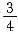 下车,男生无人下车.
下车,男生无人下车.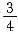 的女生和
的女生和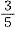 的男生都是共青团员,则该班女生人数与男生人数之比为2:3.
的男生都是共青团员,则该班女生人数与男生人数之比为2:3.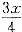 ,男生团员人数为
,男生团员人数为