银符考试题库B12
现在是:
试卷总分:100.0
您的得分:
考试时间为:
点击“开始答卷”进行答题
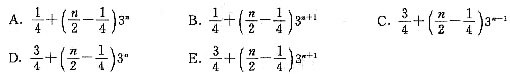
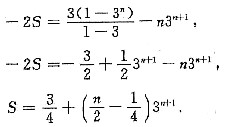
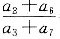 =
= 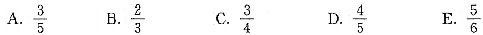
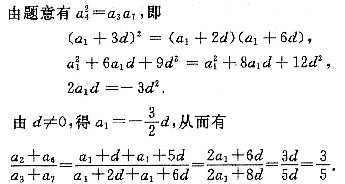


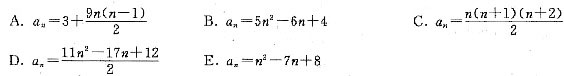
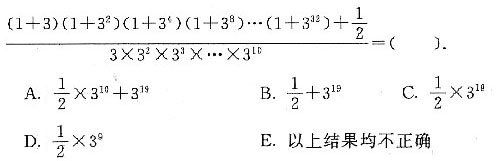
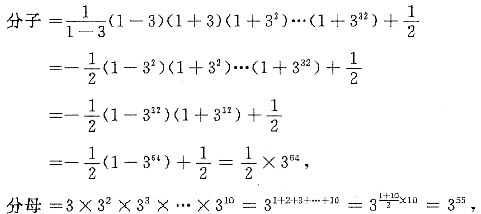

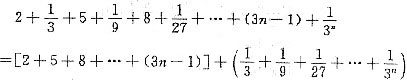
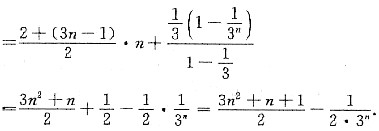
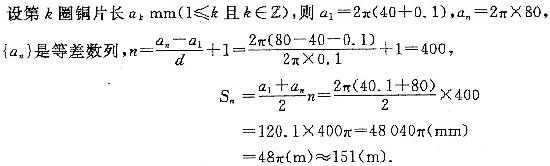
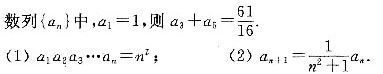
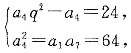
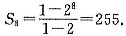
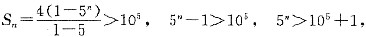
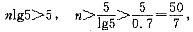
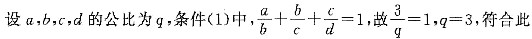

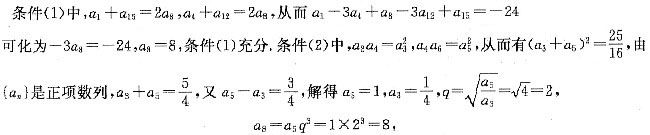
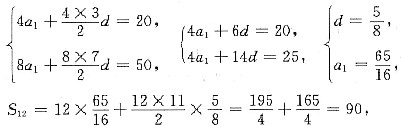
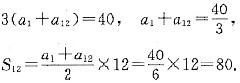


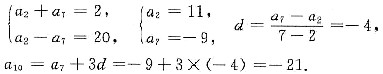
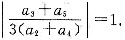
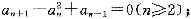
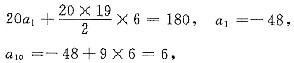
 ,则am是数列{an}中的最大项。
,则am是数列{an}中的最大项。
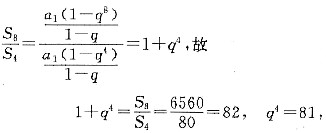
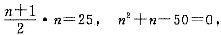
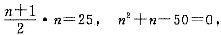 解得n=6或n=-1(舍),条件(2)充分,故选(B).
解得n=6或n=-1(舍),条件(2)充分,故选(B).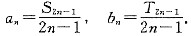
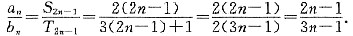
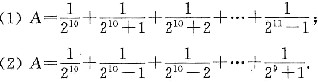
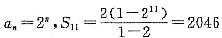 ,条件(2)也不充分.将条件(1)、条件(2)联合起来考虑,由条件(2),a1=2,a2=4,再由条件(2),a2n-1=2,a2n=4(n∈N+).
,条件(2)也不充分.将条件(1)、条件(2)联合起来考虑,由条件(2),a1=2,a2=4,再由条件(2),a2n-1=2,a2n=4(n∈N+).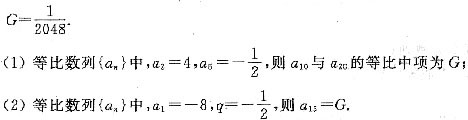


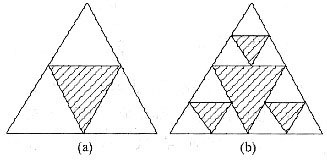
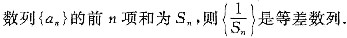


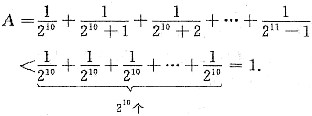
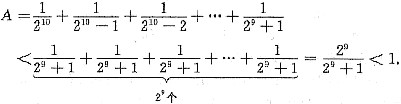
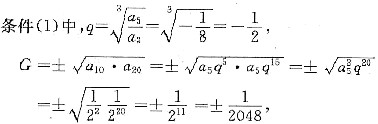
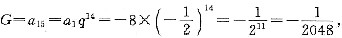
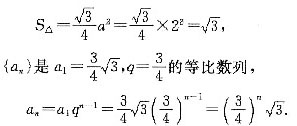


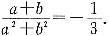
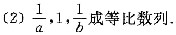


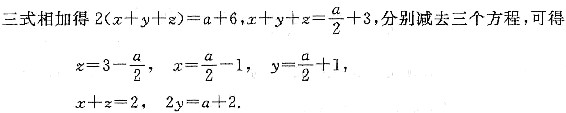
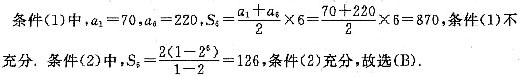
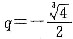 ;
;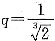 .
.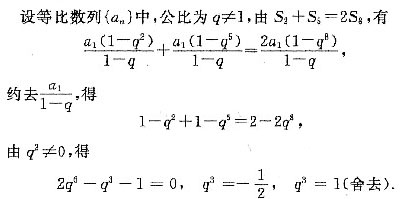
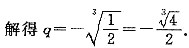
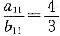 .
.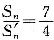 ;
;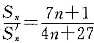 .
.
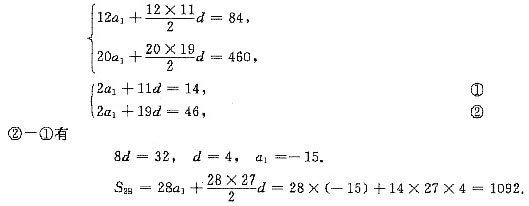
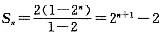 ,条件(1)不充分.条件(2)中,令an=1,{an}与{an+1}均为等比数列.但Sn=n,条件(2)也不充分.将条件(1)和条件(2)联合起来考虑,由{an}成等比数列与条件(1)有an=2qn-1,由条件(2)(an+1)也成等比数列,有a1+1,a2+1,a3+1成等比数列,从而
,条件(1)不充分.条件(2)中,令an=1,{an}与{an+1}均为等比数列.但Sn=n,条件(2)也不充分.将条件(1)和条件(2)联合起来考虑,由{an}成等比数列与条件(1)有an=2qn-1,由条件(2)(an+1)也成等比数列,有a1+1,a2+1,a3+1成等比数列,从而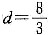 ,Sn0是前n项和Sn中的最小值;
,Sn0是前n项和Sn中的最小值;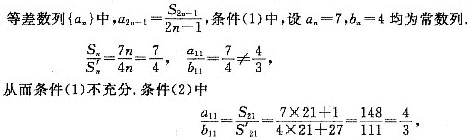
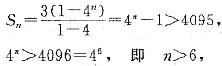
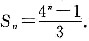
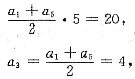
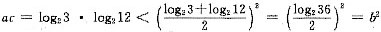 ,(由log23≠log212知以上均值不等式中等号不成立),知a,b,c不成等比数列,条件(1)充分.条件(2)中,a=b=c,常数列既是等差数列(d=0)又是等比数列(q=1),条件(2)不充分.故选(A).
,(由log23≠log212知以上均值不等式中等号不成立),知a,b,c不成等比数列,条件(1)充分.条件(2)中,a=b=c,常数列既是等差数列(d=0)又是等比数列(q=1),条件(2)不充分.故选(A).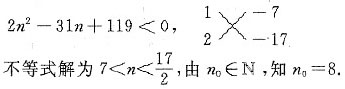
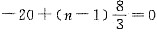 ,
,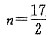 ,{an}前8项为负,第9项以后皆正,所以,S8最小,n0=8,条件(1)充分.条件(2)中,{an}是首项正公差负的递减等差数列,令an=0,即20+(n-1)(-4)=0,n=6,{an}前5项为正,第6项为零,第7项以后皆负,n=5或n=6时Sn最大,n0=5或n0=6.条件(2)不充分,故选(A).
,{an}前8项为负,第9项以后皆正,所以,S8最小,n0=8,条件(1)充分.条件(2)中,{an}是首项正公差负的递减等差数列,令an=0,即20+(n-1)(-4)=0,n=6,{an}前5项为正,第6项为零,第7项以后皆负,n=5或n=6时Sn最大,n0=5或n0=6.条件(2)不充分,故选(A).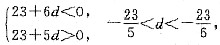
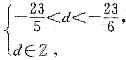
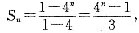
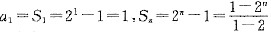 ,数列{an}是首项为1,公比为2的等比数列,an=2n-1,同条件(1)等价,条件(2)也充分.故选(D).
,数列{an}是首项为1,公比为2的等比数列,an=2n-1,同条件(1)等价,条件(2)也充分.故选(D).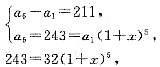
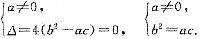
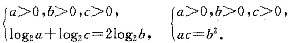
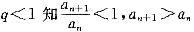 (n∈N+),因此,{an}是递增数列.故选(C).
(n∈N+),因此,{an}是递增数列.故选(C).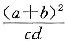 的取值范围是(-∞,0)∪(4,+∞).
的取值范围是(-∞,0)∪(4,+∞).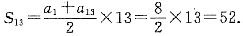
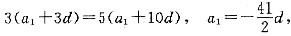
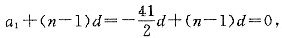
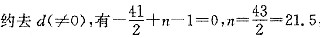 ,{an}是首项负公差正的递增等差数列,前21项均为负,从第22项开始均为正,因此Sn的最小值是S21条件(1)、条件(2)联合起来充分,故选(C).
,{an}是首项负公差正的递增等差数列,前21项均为负,从第22项开始均为正,因此Sn的最小值是S21条件(1)、条件(2)联合起来充分,故选(C).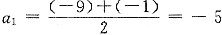 ,由条件(2),
,由条件(2),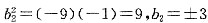 ,但b2必须与-9,-1同号(q>0,b1,b2,b3全负;q<0,b1,b3为正,b2为负),因而b2=3舍,取b2=-3,
,但b2必须与-9,-1同号(q>0,b1,b2,b3全负;q<0,b1,b3为正,b2为负),因而b2=3舍,取b2=-3,