一、填空题1. 分数单位是
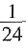
的分数中,大于
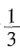
且小于
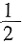
的最简分数的个数是______。
1。
[解析] 分数单位是
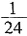
的分数中,大于
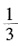
且小于
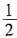
的分数共有
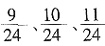
三个,其中最简分数只有
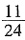
一个。
2. 一个由若干相同小正方体搭成的立体图形,从正面看是
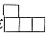
,从左面看是
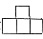
,要搭成这样的立体图形,则需要小正方体的个数至少是______。
3. 已知集合A={x|(x+1)(x-3)<0},B={x||x|>2},则A∩B等于______。
{x|2<x<3}。
[解析] 集合A={x|-1<x<3},B={x|x<-2或x>2},则
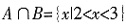
。
4. 函数y=a
x在[0,1]上的最大值与最小值的和为3,则a等于______。
2。
[解析] 由于y=ax一定是单调函数,则该函数在[0,1]上的最大值与最小值一定在x=0和x=1时取得,即a0+a1=3,解得a=2。
5. 某影院有座位60排,每排50个座位,一次报告会坐满了听众,会后留下座位号为20的所有听众进行座谈,这种抽样方法是______。
系统抽样。
[解析] 本题主要考查抽样方法的种类,本题所选取的为系统抽样方法。
6. 甲、乙两车间原有人数的比为4:3,甲车间调12人到乙车间后,甲、乙两车间的人数变为2:3,甲车间原有人数是______。
40。
[解析] 设甲车间原有4x人,乙车间原有3x人,则有
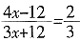
,解得x=10,所以甲车间原有40人。
另解,甲、乙两车间原来人数之比为4:3=20:15,调整后人数之比为2:3=14:21,可知甲车间减少了20-14=6份=12人,每份2人,则甲车间原有20×2=40人。
7. 对于-1≤a≤1,不等式x
2+(a-2)x+1-a>0恒成立的x的取值范围是______。
8. tan300°+cot405°的值是______。
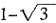
。
[解析]
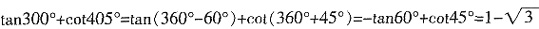
。
9. 在等差数列{a
n}中,已知a
1=2,a
2+a
3=13,则a
4+a
5+a
6等于______。
42。
[解析] 在等差数列{an}中,已知a1=2,a2+a3=13,∴d=3,a5=14,a4+a5+a6=3a5=42。
10. 在Rt△ABC中,
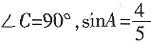
,则cosB的值等于______。
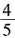
。
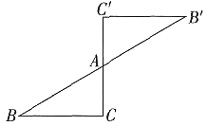
11. 如图是一个以点A为对称中心的中心对称图形,若∠C=90°,∠B=30°,AC=1,则BB'的长为______。
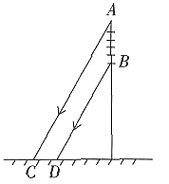
12. 如图,一根电线杆的接线柱部分AB在阳光下的影子CD的长为1米,太阳光线与地面的夹角∠ACD=60°,则AB的长为______。
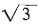
。
13.

=______
-2+4i。
[解析]
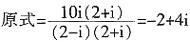
。
14. 设a>0,a≠1,则“函数f(x)=a
x在R上是减函数”,是“函数g(x)=(2-a)x
3在R上是增函数”的______。
充分不必要条件。
[解析] p:“函数f(x)=ax在R上是减函数”等价于0<a<1;q:“函数g(x)=(2-a)x3在R上是增函数”等价于2-a>0,即0<a<2且a≠1,故p是q成立的充分不必要条件。
15. 曲线
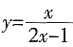
在点(1,1)处的切线方程为______。
x+y-2=0。
[解析] 先求导函数,其(1,1)处切线的斜率为-1,故切线方程为y-1=-(x-1),即x+y-2=0。
二、判断题5. 圆柱的底面半径扩大3倍,高缩小3倍,它的体积不变。
对 错
B
[解析] 圆柱的底面半径扩大3倍,高缩小3倍,它的体积增大3倍。
8. 一种商品,先降价10%,再提价10%,商品的价格与原来一样。
对 错
B
[解析] 先降价10%,再提价10%,商品的价格为99%
三、选择题1. 已知U=R,A={x|x>0),B={x|x≤-1},则
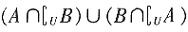
=______。
A.
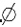
B.{x|x≤0)
C.{x|x>-1} D.{x|x>0或x≤-1}
A B C D
D
[解析] 由于
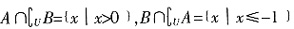
,则

。
4. 已知{a
n}是等比数列,
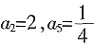
,则a
1a
2+a
2a
3+…+a
na
n+1=______。
A.16(1-4
-n) B.16(1-2
-n)
C.
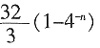
D.
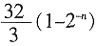
A B C D
C
[解析] 由
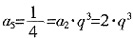
,解得
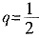
。数列a
na
n+1仍是等比数列,其首项是a
1a
2=8,公比为
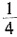
。所以,
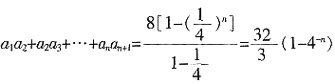
。
5. 从底面半径为1,高为4的圆柱体中掏出一个长方体,然后再在这个长方体中掏出一个最大的圆柱体,则掏出的圆柱体体积最大为______。
A.
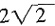
B.2
C.2π D.4π
A B C D
C
[解析] 要想掏出的圆柱体的体积最大,则要求在此之前掏出的长方体的底面为正方形,其横截面如图所示:
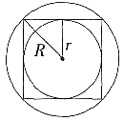
设R为大圆半径,r为小圆半径,则有
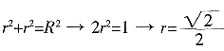
,则小圆柱体的体积为πr
2×h=π×

四、解答题1. 某商店到苹果产地收购了2吨苹果,收购价为每千克1.20元,从产地到商店的距离是400千米,运费为每吨货物每运1千米收1.50元,如果在运输及销售过程中的损耗为10%,那么商店要实现15%的利润率,零售价是每千克多少元?
设零售价为x元每千克,由题意可得:
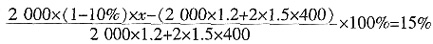
2. 甲、乙两车分别从A、B两地出发,相向而行,出发时,甲、乙的速度比是5:4,相遇后,甲的速度减少20%,乙的速度增加20%,这样,当甲到达B时,乙离A地还有10千米。那么A、B两地相距多少千米?
由题意可知,相遇后速度比为[5×(1-20%)]:[4×(1+20%)]=5:6,假设全程为9份,相遇时甲走了5份,乙走了4份,之后速度发生变化,这样甲到达B地,甲又走了4份,根据速度变化后的比值,乙应该走了4×
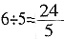
份,这样距A地还有
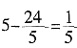
份,所以全程为
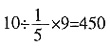
千米。
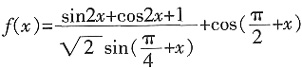 。
。3. 当
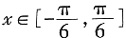
时,求f(x)的最大值;
4. 若-π<θ<0,且f(0)=2,求tanθ的值。
f(θ)=2cosθ-sinθ=2,即
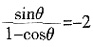
,又
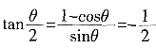
,且
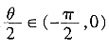
,故
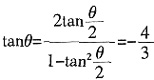
。
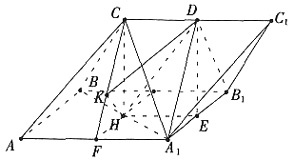
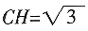 ,设D为CC1中点,
,设D为CC1中点,5. 求证:CC
1⊥平面A
1B
1D;
因为CC
1∥AA。且正方形中AA
1⊥A
1B
1,所以CC
1⊥A
1B
1,取A
1B
1中点E,则HE//BB
1∥CC
1且
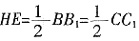
,又D为CC
1的中点,所以
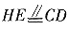
,得平行四边形HEDC,因此CH∥DE,又CH⊥平面AA
1B
1B,得CH⊥HE,DE⊥HE,所以DE⊥CC
1,故CC
1⊥平面A
1B
1D。
6. 求DH与平面AA
1C
1C所成角的正弦值。
取AA
1中点F,连CF,作HK⊥CF于K,因为CH//DE,CF∥A
1D,所以平面CFH∥平面A
1B
1D,由(1)得CG
1⊥平面A
1B
1D,所以CC
1⊥平面CFH,又HK
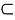
平面CFH,所以HK⊥CC
1,又HK⊥CF,得HK⊥平面AA
1C
1C,所以DH与平面AA
1C
1C所成角为∠HDK,在Rt△CFH中,
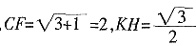
。在Rt△DHK中,由于DH=
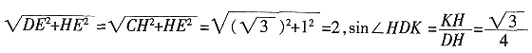
7. 求数列{a
n}的通项公式;
设等差数列{a
n}的公差为d,由已知条件可得
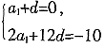
解得
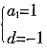
故数列{a
n}的通项公式为a
n=2-n。
8. 求数列
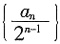
的前n项和。
设数列
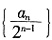
的前n项和为S
n,即
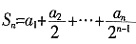
,故S
1=1,
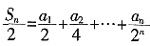
所以,当n>1时,
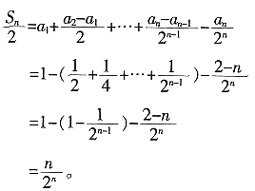
所以
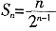
。n=1时也满足该式。
综上,数列
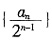
的前n项和
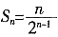
。
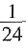 的分数中,大于
的分数中,大于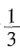 且小于
且小于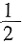 的最简分数的个数是______。
的最简分数的个数是______。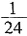 的分数中,大于
的分数中,大于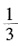 且小于
且小于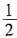 的分数共有
的分数共有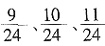 三个,其中最简分数只有
三个,其中最简分数只有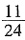 一个。
一个。 ,从左面看是
,从左面看是 ,要搭成这样的立体图形,则需要小正方体的个数至少是______。
,要搭成这样的立体图形,则需要小正方体的个数至少是______。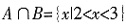 。
。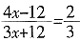 ,解得x=10,所以甲车间原有40人。
,解得x=10,所以甲车间原有40人。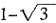 。
。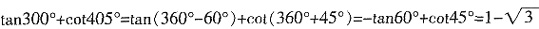 。
。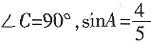 ,则cosB的值等于______。
,则cosB的值等于______。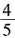 。
。

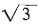 。
。 =______
=______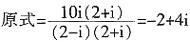 。
。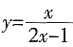 在点(1,1)处的切线方程为______。
在点(1,1)处的切线方程为______。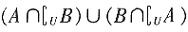 =______。
=______。 B.{x|x≤0)
B.{x|x≤0)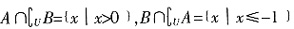 ,则
,则 。
。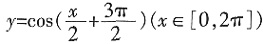 的图象和直线
的图象和直线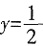 的交点个数是______。
的交点个数是______。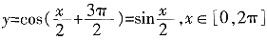 。作出原函数图象,截取x∈[0,2π]部分,其与直线
。作出原函数图象,截取x∈[0,2π]部分,其与直线 的交点个数是2个。
的交点个数是2个。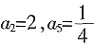 ,则a1a2+a2a3+…+anan+1=______。
,则a1a2+a2a3+…+anan+1=______。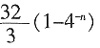
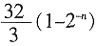
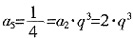 ,解得
,解得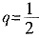 。数列anan+1仍是等比数列,其首项是a1a2=8,公比为
。数列anan+1仍是等比数列,其首项是a1a2=8,公比为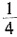 。所以,
。所以,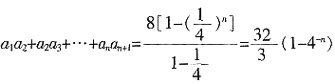 。
。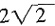 B.2
B.2
 ,则小圆柱体的体积为πr2×h=π×
,则小圆柱体的体积为πr2×h=π×
 份,这样距A地还有
份,这样距A地还有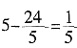 份,所以全程为
份,所以全程为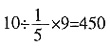 千米。
千米。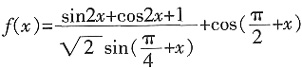 。
。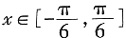 时,求f(x)的最大值;
时,求f(x)的最大值;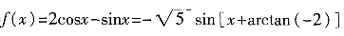 ,因
,因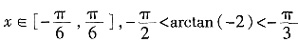 ,故x+
,故x+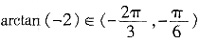 ,因此,当
,因此,当 ,即
,即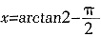 时,
时,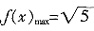 。
。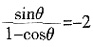 ,又
,又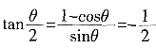 ,且
,且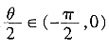 ,故
,故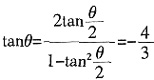 。
。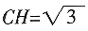 ,设D为CC1中点,
,设D为CC1中点,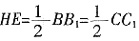 ,又D为CC1的中点,所以
,又D为CC1的中点,所以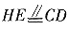 ,得平行四边形HEDC,因此CH∥DE,又CH⊥平面AA1B1B,得CH⊥HE,DE⊥HE,所以DE⊥CC1,故CC1⊥平面A1B1D。
,得平行四边形HEDC,因此CH∥DE,又CH⊥平面AA1B1B,得CH⊥HE,DE⊥HE,所以DE⊥CC1,故CC1⊥平面A1B1D。 平面CFH,所以HK⊥CC1,又HK⊥CF,得HK⊥平面AA1C1C,所以DH与平面AA1C1C所成角为∠HDK,在Rt△CFH中,
平面CFH,所以HK⊥CC1,又HK⊥CF,得HK⊥平面AA1C1C,所以DH与平面AA1C1C所成角为∠HDK,在Rt△CFH中,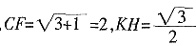 。在Rt△DHK中,由于DH=
。在Rt△DHK中,由于DH=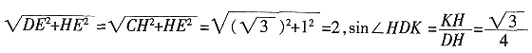

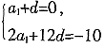
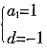
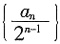 的前n项和。
的前n项和。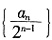 的前n项和为Sn,即
的前n项和为Sn,即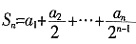 ,故S1=1,
,故S1=1,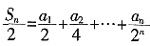
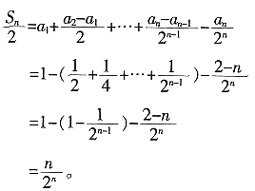
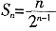 。n=1时也满足该式。
。n=1时也满足该式。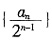 的前n项和
的前n项和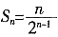 。
。