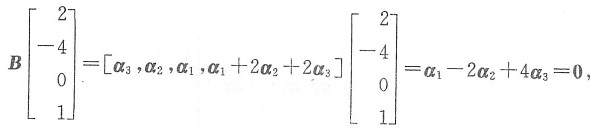一、选择题1. 设
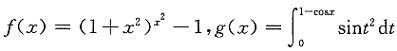
,则x→0时f(x)是g(x)的______.
- A.高阶无穷小
- B.低价无穷小
- C.同阶的非等价无穷小
- D.等价无穷小
A B C D
B
[解析] 归结为求极限
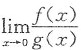
.用等价无穷小代换和洛必达法则求之.
解一
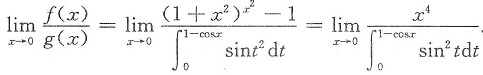
因分母为x的(2+1)×2=6阶无穷小量,而分子为x的4阶无穷小量,因而f(x)是g(x)的低阶无穷小.仅(B)入选.
解二
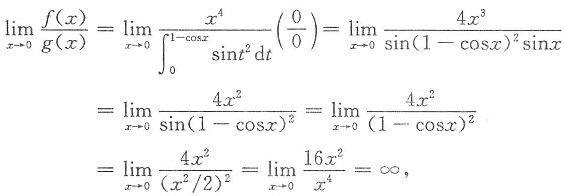
故f(x)为g(x)的低阶无穷小.仅(B)入选.
解三 f(x)~x
4(x→0),g(x)为(2+1)×2=6阶无穷小量(x→0).
显然,f(x)为g(x)的低阶无穷小.仅(B)入选.
2. 曲线r=ae
bθ(a>0,b>0),从θ=0到θ=β(β>0)的一段弧长为______.
A.
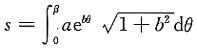
B.
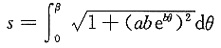
C.
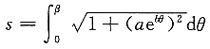
D.
A B C D
A
[解析] 利用弧长的计算公式计算.
解一
仅(A)入选.
解二 令
则其弧长公式为
仅(A)入选.
3. 设f(x),g(x)在点x=0的某邻域内连续,且f(x)具有一阶连续导数,满足

时,则______.
- A.x=0为f(x)的极小值点
- B.x=0为f(x)的极大值点
- C.(0,f(0))为曲线y=f(x)的拐点
- D.x=0不是f(x)的极值点,(0,f(0))也不是曲线y=f(x)的拐点
A B C D
C
[解析] 由题设易知f'(0)=0.为判断x=0的性质,只好考察x=0的附近f"(x)是否改变符号,如改变符号,(0,f(0))为拐点.
由
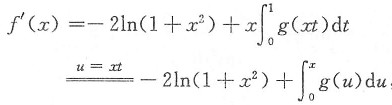
有
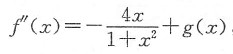
于是
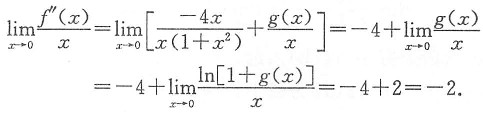
可见在x=0的左、右两侧f"(x)变号.
因此(0,f(0))为曲线y=f(x)的拐点.仅(C)入选.
4. 设f(x)是连续函数,F(x)是f(x)的原函数,则______.
- A.当f(x)是奇函数时,F(x)必是偶函数
- B.当f(x)是偶函数时,F(x)必是奇函数
- C.当f(x)是周期函数时,F(x)必是周期函数
- D.当f(x)是单调增函数时,F(x)必是单调增函数
A B C D
A
[解析] 利用f(x)的所有原函数的性质判别.
f(x)的所有原函数可写为
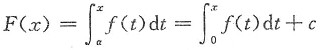
(c为任意常数).
它有下述常用的性质:
(1)若f(x)是奇函数,则
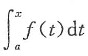
必为偶函数’
(2)若f(x)为偶函数,则只有当c=0时,
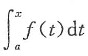
才为奇函数;
(3)若f(x)为周期函数,则存在常数T,使得对任意x,有f(x+T)=f(x),而
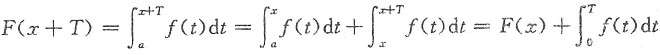
即只有
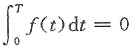
时,F(x)才是周期函数’
(4)若f(x)为单调增函数,对任意x
1,x
2,不妨设x
1<x
2,有f(x
1)<f(x
2),而
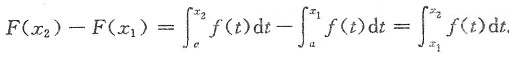
要想F(x)是单调增函数.则应有

,而由x
1,x
2的任意性知,必须有f(x)>0才行.
解一 设
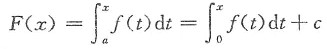
(c为任意常数),
若f(x)为奇函数,则
f(x)=-f(x),
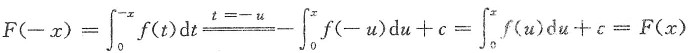
故F(x)为偶函数.仅(A)入选.
解二 令f(x)=x
2,

,则可排除(B);
令f(x)=1,F(x)=x,则可排除(C);
令f(x)=x,
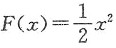
,则可排除(D);
故仅(A)入选.
6. 设
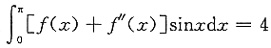
,f(0)=1,则f(π)=______.
A B C D
D
[解析] 注意到被积函数含有导函数,应先利用分部积分法求出定积分.
有人可能认为
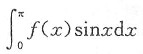
算不出来,但不要急,在计算过程中也可能产生
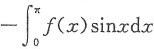
这一项,因而它会自动消失.
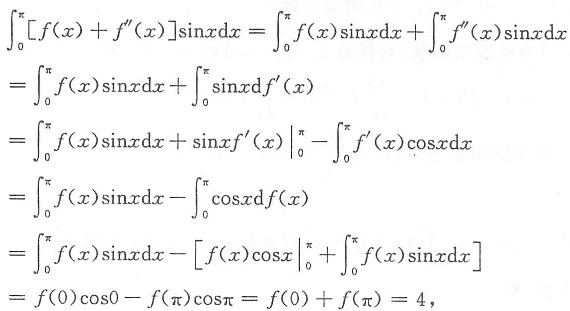
即 f(π)=4-f(0)=4-1=3.
故仅(D)入选.
8. 设A,B均为n阶方阵,且A为可逆矩阵,B为不可逆矩阵,A
*,B
*分别为A,B的伴随矩阵,则______.
- A.A*+B*必为可逆矩阵
- B.A*+B*必为不可逆矩阵
- C.A*B*必为可逆矩阵
- D.A*B*必为不可逆矩阵
A B C D
D
[解析] 可利用A
*的秩与A的秩的关系判别.当A为满秩矩阵(或为列满秩矩阵)时,还可利用秩(AB)=秩(B),简易判别.
解一 因A为可逆矩阵,故秩(A)=n,因而秩(A
*)=n,而B为不可逆矩阵,故秩(B)≤n-1,从而秩(B
*)≤1.于是
秩(A
*B
*)=秩(B
*)≤1,
故A
*B
*必为不可逆矩阵.仅(D)入选.
解二 用友证法证之.如A
*B
*可逆,由题设又知A可逆,则A
*=|A|A
-1可逆.(A
*)
-1存在,则(A
*)
-1(A
*B
*)为两个可逆矩阵的乘积,故也可逆,即
(A
*)
-1A
*B=[(A
*)
-1A
*]B
*=B
* 可逆,进而B可逆.这与题设矛盾,故A
*B
*不可逆.仅(D)入选。
解三 用排错法确定选项.设
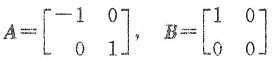
则A可逆,B不可逆,易求得

则
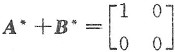
不可逆,且
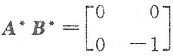
也不可逆.因而(A)、(C)都不对
如令
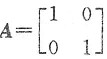
,则

.如令
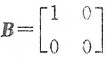
,则

因

,故A
*+B
*可逆,(B)也不对,仅(D)入选.
二、填空题1.
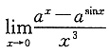
=______.
[解析] 分子为两同底指数函数差,先提公因式,再用等价无穷小代换求之.
原式
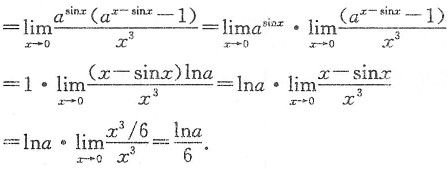
2. 设
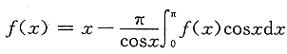
,则f(x)=______.
[解析] 注意到
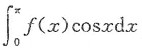
为常数,由此可先将
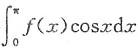
求出,再求f(x).
在式①两边同乘cosx,再在[0,π]上积分得到

故
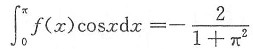
从而
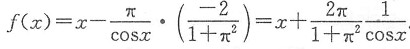
3. 设f(x)为可导的以4为周期的周期函数,且
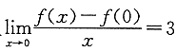
,则曲线y=f(x)在点(-4,0)处的法线方程为______.
[解析] 首先要了解导数的几何意义.在几何上,函数y=f(x)在点x
0处的导数f'(x
0)是曲线y=f(x)在点(x
0,f(x
0))处的切线斜率,因而y=f(x)过其上一点(x
0,f(x
0))的切线方程和法线方程分别为
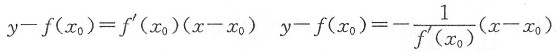
因f(x)为导数的以4为周期的周期函数,则f'(x)也是以4为周期的可导函数,即f'(-4)=f'(0).而
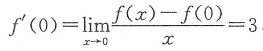
故f'(-4)=3,所以法线方程为

4. 已知
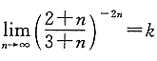
,则
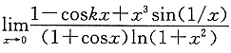
=______.
[解析] 先求出k,将其代入所求极限,用等价无穷小代换求之.k可用公式
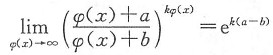
求之.
由
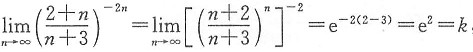
得到
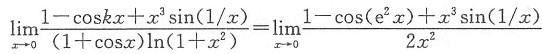
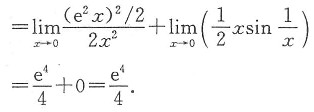
5. 已知
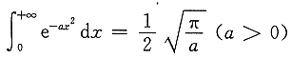
,则积分
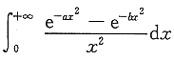
(a>0,b>0)的值等于______.
[解析] 所求积分既是无穷限的反常积分,又是带瑕点x=0的无界函数的反常积分.使用其定义,利用已知结果及分部积分法求之.
由分部积分公式得
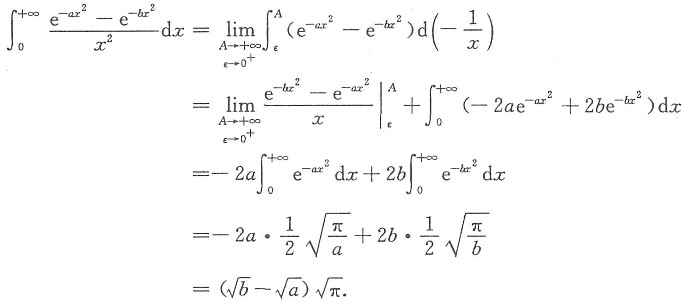
注意
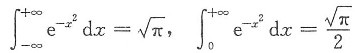
.这是常用结论应记住.
6. 设
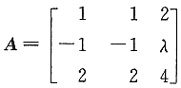
,B为三阶非零矩阵,且满足BA=O,则当λ满足______时,B的秩恰为1.
λ≠-2
[解析] 因B为三阶非零矩阵,故秩(B)≥1.下面只证秩(B)≤1.这就需要利用条件BA=O去证明.
由题设知秩(B)≥1,又由BA=O知,
秩(A)+秩(B)≤3, 即 秩(B)≤3-秩(A).
当λ≠-2时,秩(A)=2,于是有秩(B)≤3-2=1,从而秩(B)=1.
三、解答题设u=f(x,y,z),且
x=rcosθsinφ,y=rsinθsinφ,z=rcosφ,
证明:1. 若
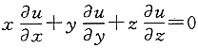
,则u仅是θ与φ的函数;
所谓u仅是θ与φ的函数,就意味着u与r无关.由于
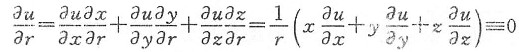
所以u不依赖于r.
仅需证明
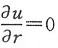
;
2. 若
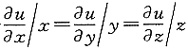
,则u仅是r的函数.
同(1)相类似,由题设得
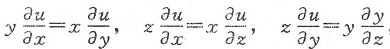
则
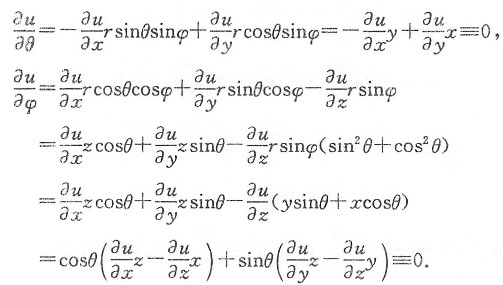
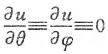
,说明u与θ、φ均无关,即u仅是r的函数,
仅需证明
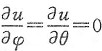
.
3. 设f(x)为在[a,b]上连续的非负函数,且在(a,b)内可导,试证:至少存在一点ξ∈(a,b),使得
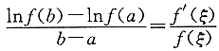
对F(x)=lnf(x)在[a,b]上使用拉格朗日中值定理.
证令F(x)=lnf(x),则F(x)在[a,b]上连续,在(a,b)内可导,且
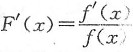
由拉格朗日中值定理知,存在ξ∈(a,b),使得
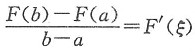
,即
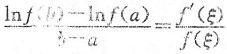
4. 设
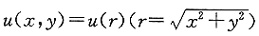
,当r≠0时有连续的二阶偏导数,且满足

求函数u(x,y).
由复合函数求导法建立u对x,y的偏导数,以及u对r的导数的关系.将题设中的方程①转化为u(r)的常微分方程,然后求出u(r).
由于u(x,y)是u(r)与

的复合函数,有
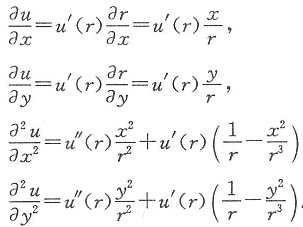
将它们相加得
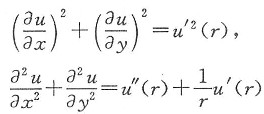
于是题设中所给方程①变成
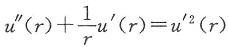
令p=u'(r),降阶得

,改写成
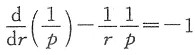
两边乘
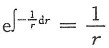
得
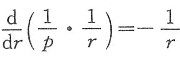
,积分得
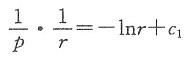
,即
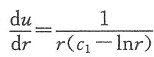
再积分得
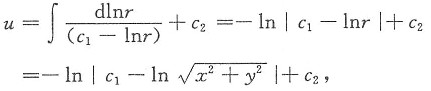
其中c
1,c
2为任意常数.
5. 设参数方程
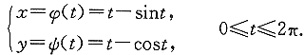
求证:
(Ⅰ)由参数方程确定连续函数y=y(x)(0≤x≤2π);
(Ⅱ)y=y(x)在[0,π]单调上升,在[π,2π]单调下降;
(Ⅲ)y=y(x)在[0,2π]是凸函数.
(1)证明x=φ(t)在[0,2π]存在连续的反函数;
(2)证明
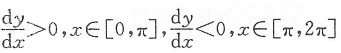
(3)证明
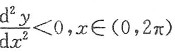
证 (Ⅰ)φ'(t)=1-cost>0(t∈(0,2π)),φ'(0)=φ'(2π)=0,
又φ(t)在[0,2π]上连续,故φ(t)在[0,2π]上单调上升,值域为
[φ(0),φ(2π)]=[0,2π],
得x=φ(t)在[0,2π]上存在连续的反函数t=t(x),定义域为[0,2π].
因此,
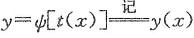
在[0,2π]上连续.
(Ⅱ)由反函数的可导性及复合函数的可导性知,y=y(x)在(0,2π)内可导,由参数式求导法,有
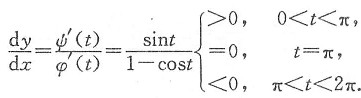
由于t∈[0,π],有x∈[0,π];t∈[π,2π],x∈[π,2π],
于是
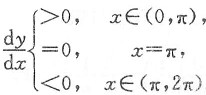
因此,y=y(x)在[0 π]上单调上升,在[π,2π]上单调下降.
(Ⅲ)由于y(x)在[0,2π]上连续,则由x∈(0,2π)时,有
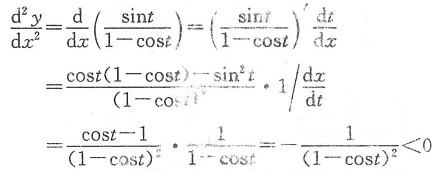
(t∈(0,2π),即x∈(0,2π).y=y(x)在[0,2π]上是凸函数.
6. 求证函数
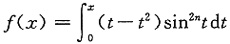
在区间(0,+∞)内的极大值不超过
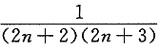
,其中n为正整数.
先求出f'(x),求出在(0,+∞)内最大值点,再利用sin
2nt<t
2n放大极(最)大值.例得证.
证 因f'(x)=(x-x
2)sin
2nx,当0<x<1时,f'(x)>0;当x>1时,f'(x)<0.故f(x)在(0,+∞)内的最大值为
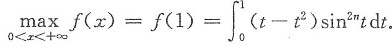
又当0<t<1时,t-t
2>0;当
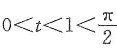
时,sint<t,有sin
2nt<t
2n.于是
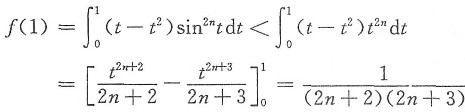
7. 设二阶可微函数满足方程
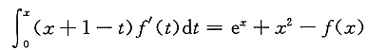
求f(x).
在所给方程两边分别对x求一阶、二阶导数以建立关于f(x)的微分方程初值问题,然后再求解,得到f(x)的表示式.
在所给方程两边关于x分别求一阶和二阶导数,得到
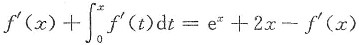
且
f'(0)=1/2,
f"(x)+f'(x)=e
x+2-f"(x).
故得微分方程的初值问题

①
则对应齐次方程的特征方程为λ
2+λ/2=0,解得
λ
1=0,λ
2=-1/2.
对应齐次方程的通解为
Y=c
1+c
2e
-x/2.
令非齐次方程的一个特解为
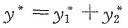
=Ax+Be
x,
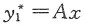
是因为1=1·e
0x,而0为特征根,故
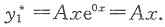
代入方程①得到A=2,B=1/3,故
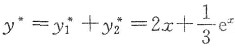
因而,原方程的通解为
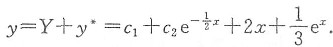
由y(0)=1,f'(0)=1/2,得到
c
1+c
2+1/3=1,-c
2/2+2+1/3=1/2,
解得c
1=-3,c
2=11/3,故
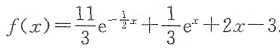
8. 设由x=0,x=π/2,y=sinx(0≤x≤π/2),y=t(0≤t≤1)所围区域的面积为S(t),求S(t)的最大值与最小值.
先根据定积分的几何意义求出S(t)的表示式,再求出其极值点.
如图所示,y=t将S(t)分为两部分,且
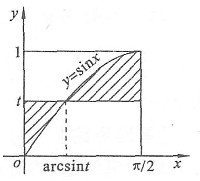

令S'(t)=0得唯一驻点
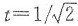
.又
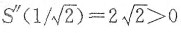
,故
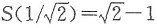
为极小值点.又S(0)=1,S(1)=π/2-1,所以S(t)的最大值为1,最小值为
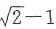
.
9. 证明α
1,α
2,…,α
3线性无关;
利用线性无关的定义证之;
令
k1α1+k2α2+…+knαn=0.
①
由题设
Aα1=α2,Aα2=α3,…,Aαn-1=αn,
有
Anα1=An-1α2=…=Aαn=0.
将An-1左乘式①,得k1αn=0.由于αn≠0,故k1=0.
再依次用An-2,An-3,…乘式①,可得
k2=k3=…=kn=0,
所以α1,α2,…,αn线性无关.
10. 求A的特征值、特征向量.
利用相关矩阵的性质求之.
由于
A[α
1,α
2,…,α
n]=[α
2,α
3,…,α
n,0]
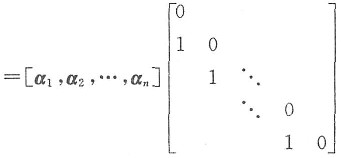
因为α
1,α
2,…,α
n线性无关,矩阵[α
1,α
2,…,α
n]可逆,从而
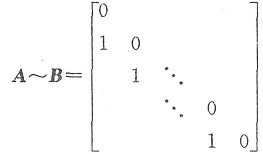
得知A的特征值全为0.又因
秩(A)=秩(B)=n-1,
所以Ax=0的基础解系由n-秩(A)=1个向量组成,由Aα
n=0·α
n知,A的线性无关的特征向量为α
n,全部特征向量为kα
n,k≠0为任意常数.
11. 已知A=[α
1,α
2,α
3,α
4]
T是四阶矩阵,α
1,α
2,α
3,α
4是四维列向量.若方程组Ax=β的通解是
[1,2,2,1]
T+k[1,-2,4,0]
T,
又B=[α
3,α
2,α
1,β-α
4],求方程组.Bx=α
1-α
2的通解.
已知方程组的通解要能由解的结构找出基础系及特解,还要能用线性方程组的向量形式求出齐次方程组与非齐次线性方程组的解.
由方程组Ax=β的解的结构,可知
秩(A)=秩(α
1,α
2,α
3,α
4)=3,
且
α
1+2α
2+2α
3+α
4=β, α
1-2α
2+4α
3=0.
因为
B=[α
3,α
2,α
1,β-α
4]=[α
3,α
2,α
1,α
1+2α
2+2α
3],
且α
1,α
2,α
3线性相关,故秩(B)=2.
由
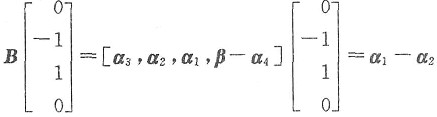
知,[0,-1,1,0]
T是方程组Bx=α
1-α
2的一个解.
又由

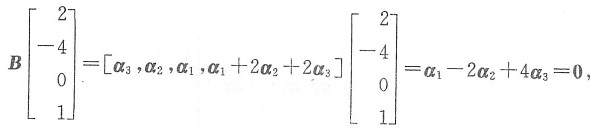
可知[4,-2,1,0]
T,[2,-4,0,1]
T是Bx=0的两个线性无关的解,故Bx=α
1-α
2的通解为
[0,-1,1,0]
T+k
1[4,-2,1,0]
T+k
2[2,-4,0,1]
T.
其中k
1,k
2为任意常数.
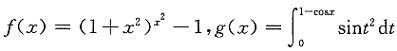 ,则x→0时f(x)是g(x)的______.
,则x→0时f(x)是g(x)的______.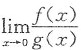 .用等价无穷小代换和洛必达法则求之.
.用等价无穷小代换和洛必达法则求之.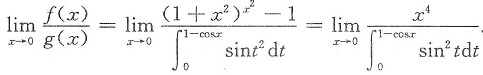
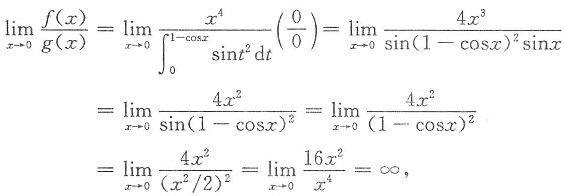
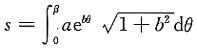
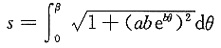
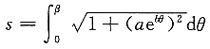
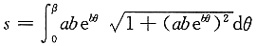
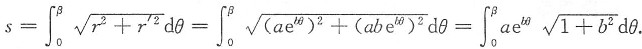
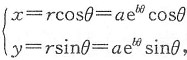 则其弧长公式为
则其弧长公式为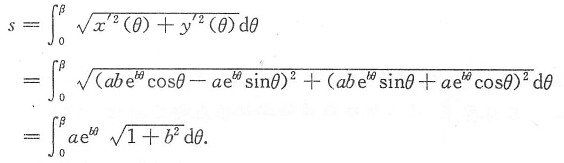
 时,则______.
时,则______.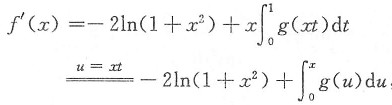
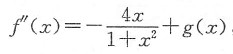
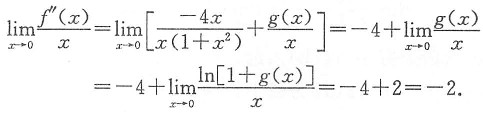
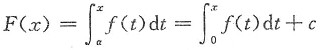 (c为任意常数).
(c为任意常数).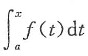 必为偶函数’
必为偶函数’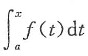 才为奇函数;
才为奇函数;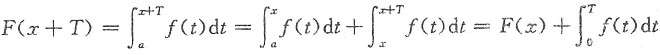
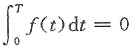 时,F(x)才是周期函数’
时,F(x)才是周期函数’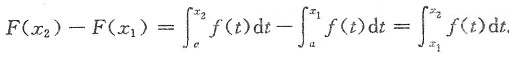
 ,而由x1,x2的任意性知,必须有f(x)>0才行.
,而由x1,x2的任意性知,必须有f(x)>0才行.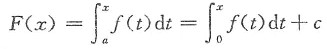 (c为任意常数),
(c为任意常数),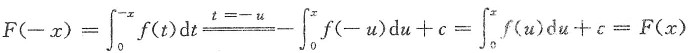
 ,则可排除(B);
,则可排除(B);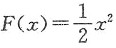 ,则可排除(D);
,则可排除(D);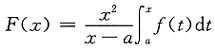 ,其中f(t)是连续函数,则
,其中f(t)是连续函数,则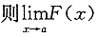 等于______.
等于______.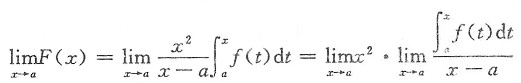
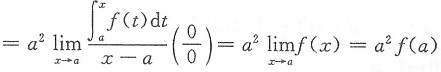
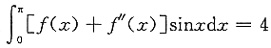 ,f(0)=1,则f(π)=______.
,f(0)=1,则f(π)=______.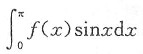 算不出来,但不要急,在计算过程中也可能产生
算不出来,但不要急,在计算过程中也可能产生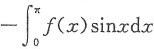 这一项,因而它会自动消失.
这一项,因而它会自动消失.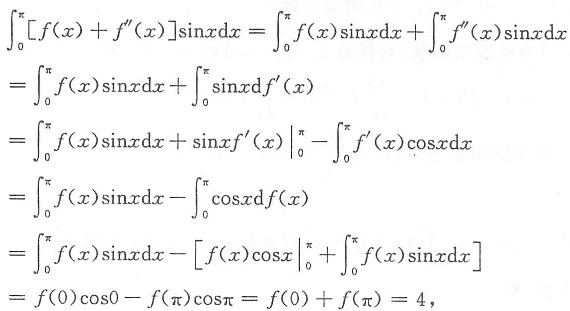
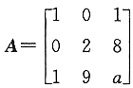 的特征值,则a=______.
的特征值,则a=______.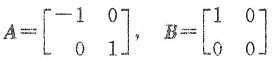

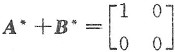 不可逆,且
不可逆,且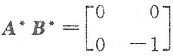 也不可逆.因而(A)、(C)都不对
也不可逆.因而(A)、(C)都不对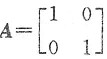 ,则
,则 .如令
.如令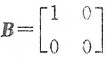 ,则
,则
 ,故A*+B*可逆,(B)也不对,仅(D)入选.
,故A*+B*可逆,(B)也不对,仅(D)入选.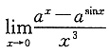 =______.
=______.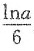
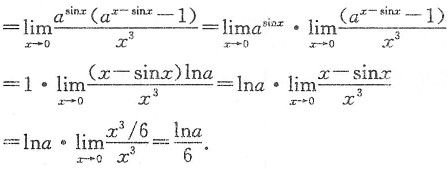
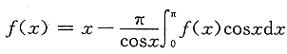 ,则f(x)=______.
,则f(x)=______.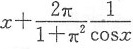
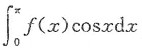 为常数,由此可先将
为常数,由此可先将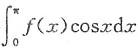 求出,再求f(x).
求出,再求f(x).
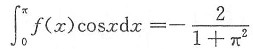
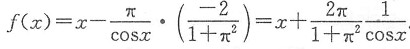
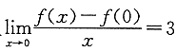 ,则曲线y=f(x)在点(-4,0)处的法线方程为______.
,则曲线y=f(x)在点(-4,0)处的法线方程为______.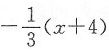
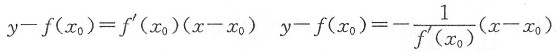
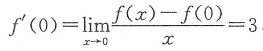

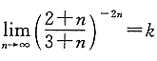 ,则
,则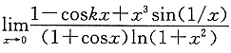 =______.
=______.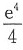
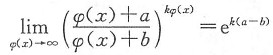
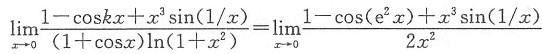
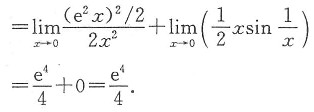
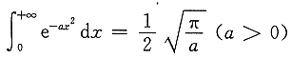 ,则积分
,则积分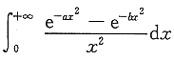 (a>0,b>0)的值等于______.
(a>0,b>0)的值等于______.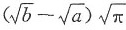
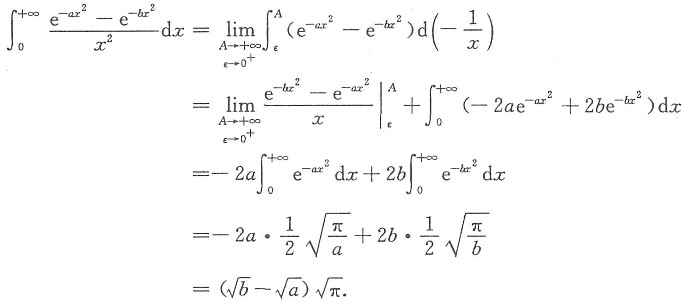
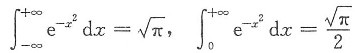 .这是常用结论应记住.
.这是常用结论应记住.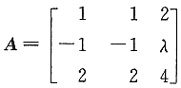 ,B为三阶非零矩阵,且满足BA=O,则当λ满足______时,B的秩恰为1.
,B为三阶非零矩阵,且满足BA=O,则当λ满足______时,B的秩恰为1.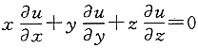 ,则u仅是θ与φ的函数;
,则u仅是θ与φ的函数;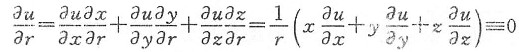
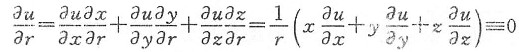
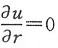 ;
;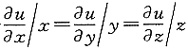 ,则u仅是r的函数.
,则u仅是r的函数.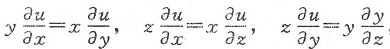
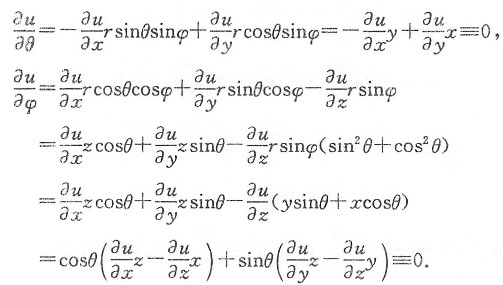
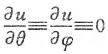 ,说明u与θ、φ均无关,即u仅是r的函数,
,说明u与θ、φ均无关,即u仅是r的函数,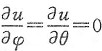 .
.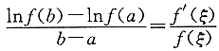
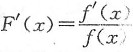
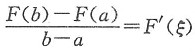 ,即
,即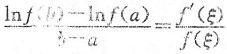
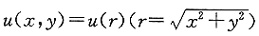 ,当r≠0时有连续的二阶偏导数,且满足
,当r≠0时有连续的二阶偏导数,且满足
 的复合函数,有
的复合函数,有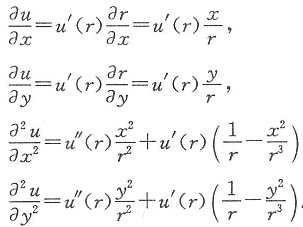
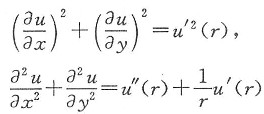
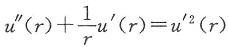
 ,改写成
,改写成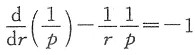
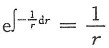 得
得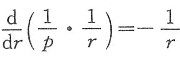 ,积分得
,积分得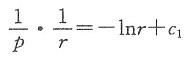 ,即
,即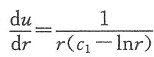
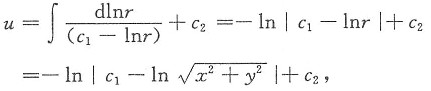
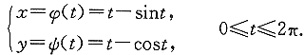
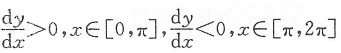
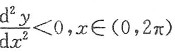
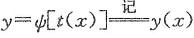 在[0,2π]上连续.
在[0,2π]上连续.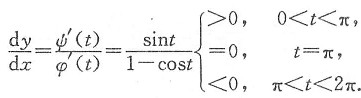
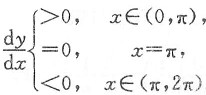
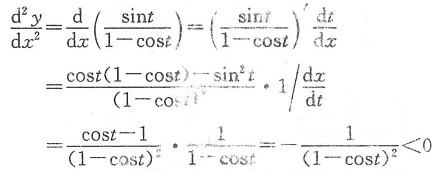
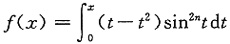 在区间(0,+∞)内的极大值不超过
在区间(0,+∞)内的极大值不超过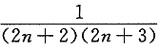 ,其中n为正整数.
,其中n为正整数.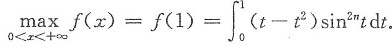
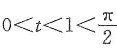 时,sint<t,有sin2nt<t2n.于是
时,sint<t,有sin2nt<t2n.于是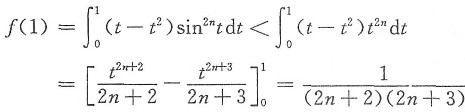
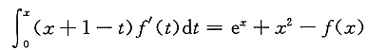
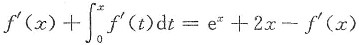
 ①
①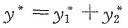 =Ax+Bex,
=Ax+Bex,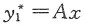 是因为1=1·e0x,而0为特征根,故
是因为1=1·e0x,而0为特征根,故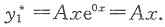
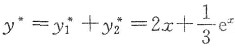
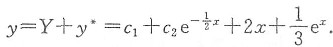
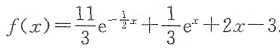


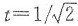 .又
.又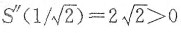 ,故
,故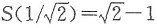 为极小值点.又S(0)=1,S(1)=π/2-1,所以S(t)的最大值为1,最小值为
为极小值点.又S(0)=1,S(1)=π/2-1,所以S(t)的最大值为1,最小值为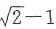 .
.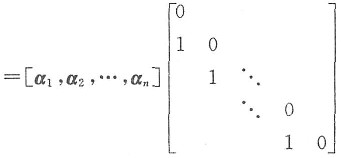

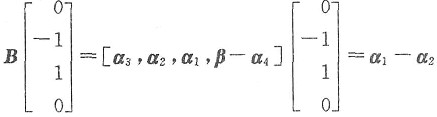 知,[0,-1,1,0]T是方程组Bx=α1-α2的一个解.
知,[0,-1,1,0]T是方程组Bx=α1-α2的一个解.