一、选择题4. 设z=y
2x,则
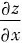
等于______.
- A.2xy2x-1
- B.2y2x
- C.y2xlny
- D.2y2xlny
A B C D
D
本题考查的知识点为偏导数的运算.
z=y
2x,若求
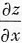
,则需将z认定为指数函数.从而有
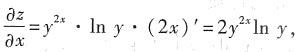
可知应选D.
8. 二元函数z=(x+1)
y,则
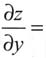
______.
- A.xy
- B.yxy
- C.(x+1)yln(x+1)
- D.y(x+1)y-1
A B C D
C
[解析] z=(x+1)
y,求
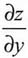
时,认定x为常量,因此z为y的指数函数.
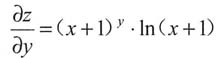
,因此选C.
二、填空题1. 设

,则f'(0)=______.
2. 设f(x+1)=x
2-3x+4,则f(x)=______.
3. 设函数y=x
2+sinx,则dy______.
(2x+cosx)dx
[解析] 本题考查的知识点为微分运算.
解法1 利用dy=y'dx.由于y'=(x2+sinx)'=2x+cosx,
可知 dy=(2x+cosx)dx.
解法2 利用微分运算法则dy=d(x2+sinx)=dx2+dsinx=(2x+cosx)dx.
4. 已知y
(n-2)=xln x,则y
(n)______。
5. 过点M
0(1,-1,0)且与平面x-y+3z=1平行的平面方程为______.
(x-1)-(y+1)+3z=0(或x-y+3z=2).
[解析] 本题考查的知识点为平面方程.
已知平面π1:x-y+3z=1的法线向量n1=(1,-1,3).所求平面π与π1,平行,则平面π的法线向量n∥n1,可取n=(1,-1,3),由于所给平面过点M0(1,-1,0).由平面的点法式方程可知所求平面方程为
(x-1)-[y-(-1)]+3(z-0)=0,
即 (x-1)-(y+1)+3z=0,
或写为 x-y+3z=2.
6. 微分方程y'-y=1的通解为______.
y=Cex-1
[解析] 本题给定方程是可分离变量的微分方程,也是一阶线性微分方程.
解法Ⅰ
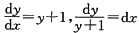
,
ln(y+1)=x+C
1,
y+1=Ce
x(其中
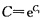
),即通解为y=Ce
x-1.
解法Ⅱ p(x)=-1,q(x)=1.
y=e
-∫p(x)dx[∫q(x)e
∫p(x)dxdx+C]-e
∫dx[∫e
∫dxdx+C]=e
x[∫e
-xdx+C]
=e
x[-e
-x+C]=Ce
x-1.
7. 设
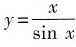
,则y'=______.
[解析] 本题考查的知识点为导数的四则运算.
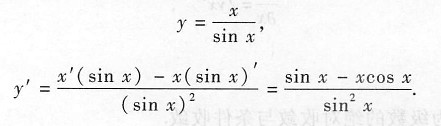
8.

9.
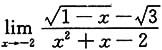
=______.
10.
