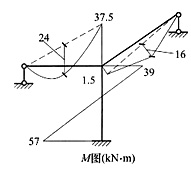
二、计算题1. 试确定下图所示结构位移法基本未知量数目和基本结构。两根链杆a和b需考虑变形。
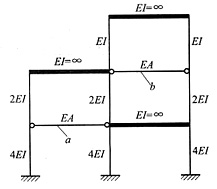
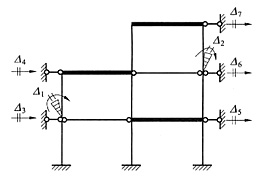
有7个基本位移未知量,基本结构如下图所示。
2. 用位移法计算下图所示刚架结构并作其弯矩图。

令

,其基本体系(注意各杆线刚度)和结构弯矩图如下图(a)、(b)所示。

3. 用位移法计算下图所示结构,并作M图,EI=常数。

M图如下图所示。

4. 用位移法作下图所示结构M图。EI=常数。

令

,基本体系如下图(a)所示。
位移法基本方程:

绘制

、M
P图如下图(b)~(d)所示。
系数及自由项:k
11=16i,

,
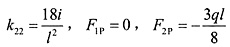
。
代入得位移法方程:

解方程得:

弯矩图如下图(e)所示。

5. 用位移法计算下图所示结构,并作M图。各杆材料相同。

本题含有结点力偶,需注意。将B、C结点角位移分别看作Δ
1和Δ
2(顺时针)。
求得

,k
12=k
21=E
I,k
22=7EI,F
1P=20kN·m,F
2P=-40kN·m。
解得
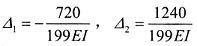
。
M图如下图所示。
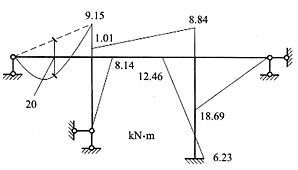
6. 用位移法计算下图所示结构,并作M图。已知:q=16.5kN/m,各杆l=4m,EI=常数。
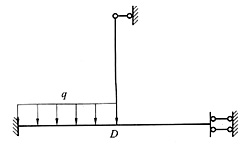
本题取

、Δ
D(↓)为基本未知量,令

,用位移法求得φ
D=8.8,Δ
D=61.6。结构M图如下图所示。

7. 用位移法计算下图所示结构,并作出其M图。各杆的EI=常数。
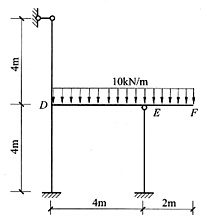
本题只取

、Δ
D(→)为基本未知量,EF段可按悬臂处理,所以只有两个基本未知量。令

,可得
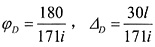
。结构M图如下图所示。

8. 用位移法计算下图所示结构并作其弯矩图。

本题只取

、Δ
E(→)为基本未知量。结构M图如下图所示。

9. 用位移法计算下图所示结构,作M图。

本题只取

、Δ
D(→)为基本未知量,并可求得

。结构M图如下图所示。

10. 用位移法作下图所示结构弯矩图,写出分析过程。

本题只有两个水平线位移基本未知量。结构M图如下图所示。

11. 作下图所示结构的弯矩图。i为各杆线刚度,忽略轴向变形的影响。
利用对称性取半结构如下图(a)所示,整个结构M图如下图(b)所示。

12. 用位移法作下图所示结构M图,EI=常数。

结构M图如下图所示。
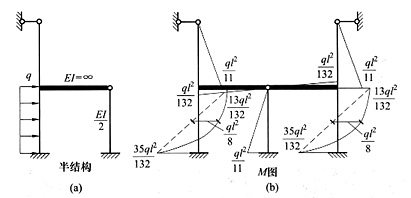
13. 用位移法计算下图所示对称刚架,作M图。已知EI
1=∞,其余各杆EI=常数,q=4kN/m。

结构M图如下图所示。

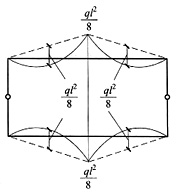
14. 试用较简便的方法作下图所示结构的弯矩图。除注明者外,其他杆件的EI为常数。

利用对称性取半结构如下图(a)所示(注意中间柱刚度减半),整个结构M图如下图(b)所示(中间柱弯矩为半结构弯矩的2倍)。
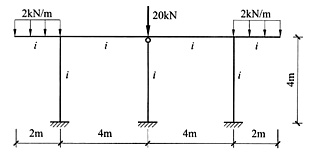
15. 计算下图所示结构(忽略轴向变形),并作出弯矩M图。EI=常数。

由于忽略轴向变形,故右侧三个刚架受弯状态相同,且都只有一个结点角位移,计算亦相同。整个结构M图如下图所示。

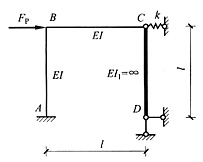
16. 试用位移法绘制下图所示结构的弯矩图,已知C点处弹簧刚度系数k=EI/l
3。
M图如下图所示。

17. 作出下图所示结构的弯矩图,横梁的刚度无穷大,柱子的刚度EI=常数,弹簧的刚度系数k=3EI/8。

M图如下图所示。

18. 用位移法计算下图所示结构并作M图。

M图如下图所示。