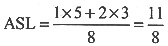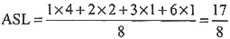一、单项选择题 (下列每题给出的4个选项中,只有一个最符合试题要求)
4. 在对长度为n的顺序存储的有序表进行折半查找时,对应的二叉判定树的高度为______。
A.n
B.
C.
D.
D
[解析] 折半查找的平均查找长度可用二叉判定树分析,其高度与完全二叉树相同,根据完全二叉树的性质,有
。
19. 对于长度为9的有序顺序表,若采用折半查找,在相等查找概率的情况下查找成功的平均查找长度为______,查找不成功的平均查找长度为34/10。
C
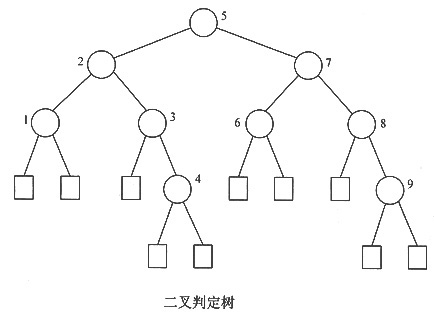
[解析] 在长度为9的有序顺序表中进行折半查找,在相等查找概率下的查找性能可以用如下图所示的二叉判定树来分析。
每个圆形结点代表表中的一个数据元素,结点旁边附加的数字是该数据元素在表中的序号。在相等查找概率的情况下,查找成功的平均查找长度和查找不成功的平均查找长度分别为
ASL
succ =(1×1+2×2+3×4+4×2)/9=25/9
ASL
unsucc =(3×6+4×4)/10=34/10
20. 下面关于m阶B树的说法中,正确的是______。
①每个结点至少有两棵非空子树
②B树中每个结点至多有m-1个关键字
③所有失败结点在同一层次上
④当插入一个索引项引起B树结点分裂后,树长高一层
B
[解析] 根据m阶B树的定义,每个结点至多有m棵子树,所以至多有m-1个关键字;所有失败结点都在同一层上,所以②③正确。①④不正确,因为除根结点之外所有非失败结点至少有
棵子树;当插入一个索引项引起B树结点分裂后,只有当根结点需要分裂时,树才长高一层。综合以上分析,本题选B。
22. 含有n个结点(不包括失败结点)的m阶B树至少包含______个关键字。
A.n
B.(m-1)×n
C.
D.
D
[解析] 根据m阶B树的定义,除根结点之外所有非失败结点至少有
棵子树,所以除根结点之外的所有非失败结点至少有
-1个关键字,根结点至少有1个关键字,所以共有(n-1)×(
-1)+1个关键字。
25. 在一棵含有n个关键字的m阶B树中进行查找,至多读盘______次。
A.log
2 n
B.1+log
2 n
C.
D.
C
[解析] 在具有n个关键字的m阶B树中进行查找时,从根结点到关键字所在结点的路径上所涉及的结点数最多等于树的高度
,而每访问一个结点,最多读1次盘,因此读盘次数最多为h。
27. 如果在一棵m阶B树中删除关键字导致结点需要与其右兄弟或左兄弟结点合并,那么被删关键字所在结点的关键字数在删除之前应为______。
A.
B.
C.
D.
B
[解析] 根据m阶B树的定义,除根结点之外每个非失败结点至少有
个关键字。因为在B树中不论被删关键字在哪一层的结点上,最后都能归结到叶结点上的删除。如果在删除关键字之前叶结点中关键字数已经是
,那么在删除关键字之后该结点的关键字数不足
就必须进行结点的调整,当然不一定是结点合并,还要看兄弟结点内的关键字数。但如果要做结点合并,其兄弟结点关键字数一定也是
。
30. 设高度为h的m阶B树有n个关键字,即第h+1层是失败结点,那么n至少为______。
A.
B.
C.
D.
A
[解析] 根据m阶B树最大高度的推导,到了失败结点这一层
,因此有n≥
。
二、综合应用题 1. 给出在一个递增有序表A中采用二分查找算法查找值为x的元素的递归算法。
每次在当前序列中取序列中点作为区域划分界限,然后对子区域分别递归地进行查找即可,代码如下:
2. 使用散列函数:
H(k)=3k mod 11
并采用链地址法处理冲突。试对关键字序列(22,41,53,46,30,13,01,67)构造哈希表,求等概率情况下查找成功的平均查找长度,并设计构造哈希表的完整的算法。
本题的哈希表构造过程如下:
(1)H(22)=3*22 mod 11=0
(2)H(41)=3*41 mod 11=2
(3)H(53)=3*53 mod 11=5
(4)H(46)=3*46 mod 11=6
(5)H(30)=3*30 mod 11=2
(6)H(13)=3*13 mod 11=6
(7)H(1)=3*01 mod 11=3
(8)H(67)=3*67 mod 11=3
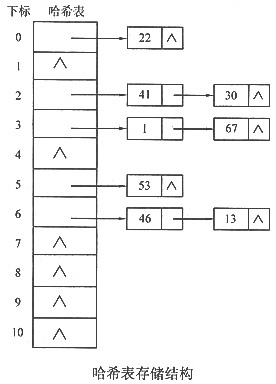
用链表法解决冲突的哈希表存储结构如下图所示。
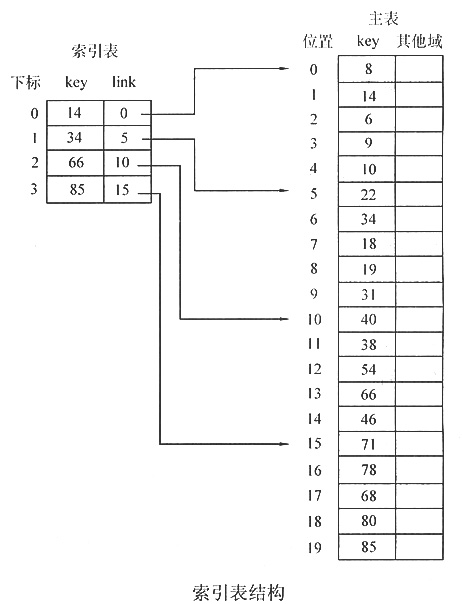
查找成功的平均查找长度为
构造本哈希表的程序代码如下:
typedef struct node
{
int key;
struct node *next;
} hashnode;
hashnode ht[M]; //假设M是已经定义的常量
void chash()
{
int x[]={22,41,53,46,30,13,1,67},i,j;
hashnode *p;
for(i=0;i<M;++i) //表头均置空
ht[i].next=NULL;
for(i=0;i<N;++i) //假设N是已经定义的常量
{
p=(hashnode *)malloc(sizeof(hashnode));
p=>key=x[i];
j=(3*x[i]) % M;
p->next=ht[j].next; //将p结点插入到ht[j]之后
ht[j].next=p;
}
}
3. 给定整型数组B[0,…,M][0,…,N]。已知B中数据在每一维方向上都按从小到大的次序排列,且整型变量x在B中存在。设计一个程序段,找出一对满足B[i][j]=x的i,j值,找到后输出i和j的值,要求比较次数不超过M+N。
实现本题功能的程序代码如下,可以验证其比较次数不超过m+n。
4. 编写一个函数,利用二分查找算法在一个有序表中插入一个元素x,并保持表的有序性。
先在有序表r中利用二分查找算法查找关键字值等于或小于x的结点,m指向正好等于x的结点或l指向关键字正好大于x的结点,然后采用移动法插入x结点即可。
5. 以下图所示的索引表结构为例,设计一个进行数据查找的算法。
先在索引表I中找出x在主表中的位置区间[1,h],由于索引表按关键字key的顺序排序,所以这里的查找采用二分查找法。然后在主表A中的[1,h]区间中查找元素x,由于主表是无序的,所以这里的查找采用顺序查找法。
6. 使用散列函数:
H(k)=3k mod 11
并采用开放地址法处理冲突,所求下一地址函数为
d
1 =H(k)
d
i =(d
i-1 +((7k mod 10)+1)%11(i=2,3,…)
试在0~10的散列地址空间中对关键字序列(22,41,53,46,30,13,01,67)构造哈希表,求等概率情况下查找成功的平均查找长度,并设计构造哈希表的完整的算法。
本题的哈希表构造过程如下:
(1)H(22)=3*22 mod 11=0比较1次
(2)H(41)=3*41 mod 11=2比较1次
(3)H(53)=3*53 mod 11=5比较1次
(4)H(46)=3*46 mod 11=6比较1次
(5)H(30)=3*30 mod 11=2冲突
d1=H(30)=2
H(30)=(2+(7*30 mod 10)+1)mod 11=3比较2次
(6)H(13)=3*13 mod 11=6冲突
d1=H(13)=6
H(13)=(6+(7*13 mod 10)+1)mod 11=8比较2次
(7)H(1)=3*01 mod 11=3冲突
d1=H(1)=3
H(1)=(3+(1*7 mod 10)+1)mod 11=0冲突
d2=H(1)=0
H(1)=(0+(1*7 mod 10)+1)mod 11=8冲突
d3=H(1)=8
H(1)=(8+(1*7 mod 10)+1)mod 11=5冲突
d4=H(1)=5
H(1)=(5+(1*7 mod 10)+1)mod 11=2冲突
d5=H(1)=2
H(1)=(2+(1*7 mod 10)+1)mod 11=10比较6次
(8)H(67)=3*67 mod 11=3冲突
d1=H(67)=3
H(67)=(3+(7*67 mod 10)+1)mod 11=2冲突
d2=H(67)=2
H(67)=(2+(7*67 mod 10)+1)mod 11=1比较3次
构造本哈希表的程序代码如下:
struct hterm
{
int key; //关键字值
int si; //散列次数
};
struct hterm hlist[M]; //假设M=11是已定义的常量
int i,adr,sum,d;
int x[N]={22,41,53,46,30,13,1,67}; //关键字赋值
//假设N=8是已定义的常量
float average;
void chash() //创建哈希表
{
for(i=0;i<M;++i) //置初值
{
hlist[i].key=0;
hlist[i].si=0;
}
for(i=0;i<N;++i)
{
sum=0;
adr=(3*x[i]) % M;
d=adr;
if(hlist[adr].key==0)
{
hlist[adr].key=x[i];
hlist[adr].si=1;
}
else
{
do //处理冲突
{
d=(d+(x[i]*7) % 10+1) % M;
sum=sum+1;
} while(hlist[d].key!=0);
hlist[d].key=x[i];
hlist[d].si=sum+1;
}
}
}
7. 使用散列函数:
H(k)=3k mod 11
采用开放地址法处理冲突时,设计一个算法查找一个指定元素值的位置。
实现本题功能的函数代码如下:
8. 使用散列函数:
H(k)=3k mod 11
采用链地址法处理冲突时,设计一个算法删除一个指定的结点。
实现本题功能的函数代码如下:
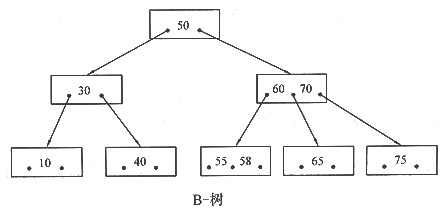
9. 有一棵如下图所示的B-树(m=3),设计一个算法对其进行先序遍历(遍历到结点时直接输出结点中的关键字)和查找给定值的结点,要求写出B-树结点结构。
对B-树的线序遍历和查找算法与二叉排序树相应的算法相似。
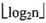
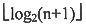
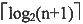
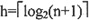 。
。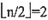 。
。
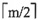 棵子树;当插入一个索引项引起B树结点分裂后,只有当根结点需要分裂时,树才长高一层。综合以上分析,本题选B。
棵子树;当插入一个索引项引起B树结点分裂后,只有当根结点需要分裂时,树才长高一层。综合以上分析,本题选B。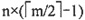
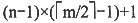
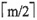 棵子树,所以除根结点之外的所有非失败结点至少有
棵子树,所以除根结点之外的所有非失败结点至少有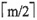 -1个关键字,根结点至少有1个关键字,所以共有(n-1)×(
-1个关键字,根结点至少有1个关键字,所以共有(n-1)×(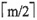 -1)+1个关键字。
-1)+1个关键字。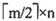
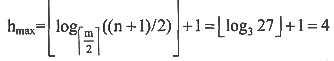 。
。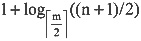
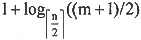
 ,而每访问一个结点,最多读1次盘,因此读盘次数最多为h。
,而每访问一个结点,最多读1次盘,因此读盘次数最多为h。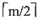
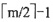
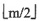
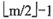
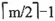 个关键字。因为在B树中不论被删关键字在哪一层的结点上,最后都能归结到叶结点上的删除。如果在删除关键字之前叶结点中关键字数已经是
个关键字。因为在B树中不论被删关键字在哪一层的结点上,最后都能归结到叶结点上的删除。如果在删除关键字之前叶结点中关键字数已经是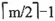 ,那么在删除关键字之后该结点的关键字数不足
,那么在删除关键字之后该结点的关键字数不足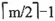 就必须进行结点的调整,当然不一定是结点合并,还要看兄弟结点内的关键字数。但如果要做结点合并,其兄弟结点关键字数一定也是
就必须进行结点的调整,当然不一定是结点合并,还要看兄弟结点内的关键字数。但如果要做结点合并,其兄弟结点关键字数一定也是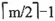 。
。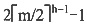
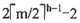
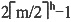
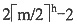
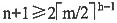 ,因此有n≥
,因此有n≥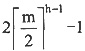 。
。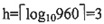 。
。