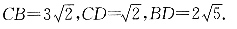一、单项选择题1. 复数
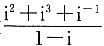
等于______.
A.
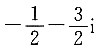
B.
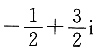
C.
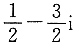
D.
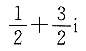
A B C D
C
[解析]
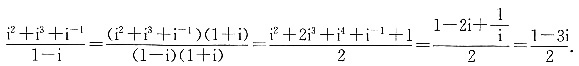
12. 一个圆锥的侧面展开图是半径为1的半圆,则该圆锥的底面半径是______.
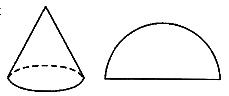
A.1
B.
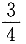
C.
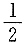
D.9
A B C D
C
[解析] 设圆锥底面半径为r,根据题意得:
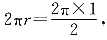
解得
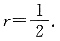
14. 已知a=3,且
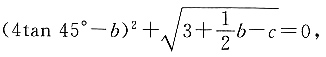
以a,b,c为边长组成的三角形面积等于______.
A B C D
A
[解析] 因为
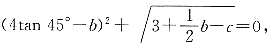
所以4tan 45°-b=0,3+
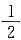
b-c=0,所以b=4,c=5.又因为a
2+b
2=9+16=25=c
2,所以△ABC是直角三角形,且a,b为两条直角边,所以△ABC的面积
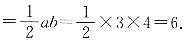
故选A.
二、填空题1. 已知平面π
1:x+2y-5z+7=0与平面π
2:4x+3y+mz+13=0垂直,则m=______.
2
[解析] 两平面的法向量分别为:n
1=(1,2,-5);n
2=(4,3,m),由两平面垂直
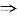
4+6-5m=0
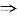
m=2.
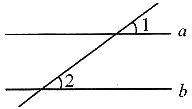
2. 如下图,已知直线a∥b,∠1=40°,则∠2=______.
40°
[解析] 因为直线a∥b,∠1和∠2为同位角,所以∠1=∠2=40°.
3. 已知函数
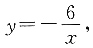
当x=-2时,y的值是______.
4. 在Rt△ABC中,∠C=90°,
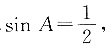
则∠A=______.
30°
[解析] 因为在Rt△ABC中,∠C=90°,所以∠A为锐角,且

所以∠A=30°.
5. 已知关于x的方程3x-2m=4的解是x=m,则m的值是______.
4
[解析] 因为x=m是该方程的解,所以将其代入方程,方程仍成立,即3m-2m=4,m=4.
三、解答题1. 如下图,直线y=kx将抛物线y=2x-x
2与x轴所围成的图形分为面积相等的两个部分,求k的值.
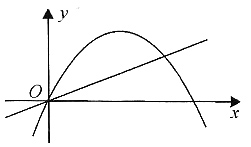
解:抛物线y=2x-x
2与x轴两交点的横坐标为x
1=0,x
2=2,所以抛物线与x轴所围图形的面积
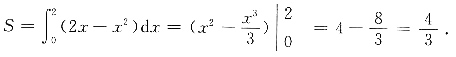
抛物线y=2x-x
2与y=kx两交点的横坐标为x'=0,x'
2=2-k,
所以
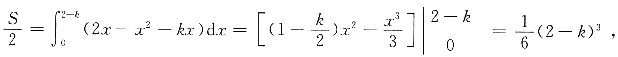
又知
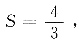
所以(2-k)
3=4,则

2. 已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球.现从甲、乙两个盒内各任取2个球.设ξ为取出的4个球中红球的个数,求ξ的分布列和数学期望.
解:由题意,ξ可取0,1,2,3.
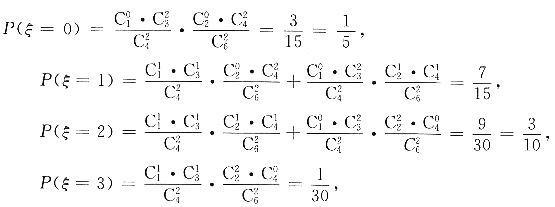

3. 已知椭圆
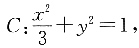
设直线l与椭圆C交于A、B两点,坐标原点O到直线l的距离为
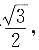
|AB|的最大值.
解:设直线l为y=kx+b,联立方程组
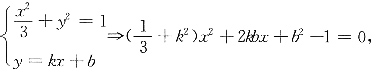
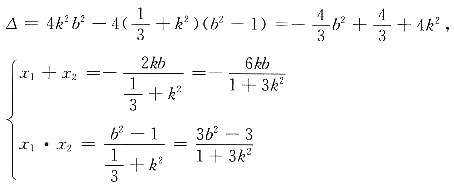
(1)当AB⊥x轴时,
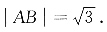
(2)当AB与x轴不垂直时,设直线l的方程为y=kx+m,A(x
1,y
1),B(x
2,y
2),
原点O到直线l的距离为
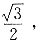
所以
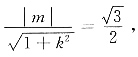
得到
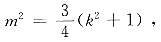
将y=kx+m代入椭圆方程得到
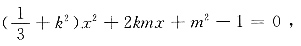
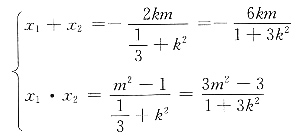
则
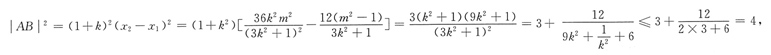
所以当且仅当
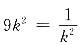
时,|AB|
2取最大值4,则|AB|最大值为2.
(3)当k=0时,
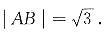
所以,综合上述情况,|AB|最大值为2.
4. 求f(x)的导函数f'(x)的最小值;
解:f(x)=e
x-e
-x-ax,所以
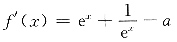
因为e
x>0恒成立,所以
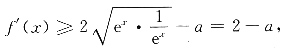
即f'(x)最小值为2-a.
5. 若对所有x≥0都有f(x)≥0,求a的取值范围.
解:因为对于所有x≥0,都有f(x)≥0,而f(0)=0,所以f(x)≥0,
即e
x+e
-x-a≥0
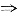
e
x+e
-x≥a,又因为e
x+e
-x≥2,所以a≤2.
6. 已知数列{a
n}中,a
1=a,S
n是数列{a
n}的前n项和,且满足S
n+S
n-1=3n
2(n=2,3,4,…),试确定a的取值集合M,使a∈M时,数列{a
n}是单调递增数列.
解:由题S
n+S
n-1=3n
2 ①
S
n+1+S
n=3(n+1)
2 ②
②-①得:
S
n+1-S
n-1=a
n+1+a
n=6n+3 ③
同理,S
n+2-S
n=a
a+2+a
n+1=6(n+1)+3=6n+9 ④
④-③得
a
n+2-a
n=6
再由S
2+S
1=3×2
2=12
得a
2=12-2a
1=12-2a
a
4=18-2a
a
6=24-2a
.
.
.
a
2k=6(k+1)-2a (k∈N
+)
同理得a
2k+1=6k-3+2a (k∈N
+)
由题意{a
n}是单调递增数列有:
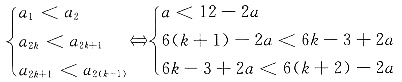
解得:
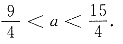
所以
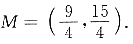
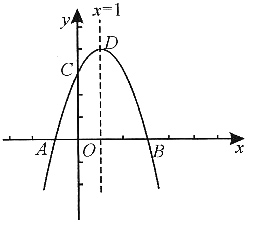
7. 直接写出抛物线与x轴另一个交点B的坐标;
解:抛物线与x轴的一个交点坐标为(-1,0),且对称轴为直线x=1,则抛物线与x轴的另一个交点坐标为(3,0).
8. 求抛物线的解析式;
解:设抛物线的方程为y=ax
2+bx+c,则根据题意得:
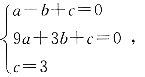
解得
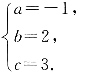
所以抛物线的解析式为:y=-x
2+2x+3.
9. 设抛物线的顶点为D,在其对称轴的右侧的抛物线上是否存在点P,使得△PDC是等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;
解:存在.由y=-x
2+2x+3得,D点坐标为(1,4),对称轴为x=1.
①若以CD为底边,则PD=PC,设P点坐标为(x,y).
根据两点间距离公式得x
2+(3-y)
2=(x-1)
2+(y-4)
2,即y=4-x.又P点(x,y)在抛物线上,所以4-x=-x
2+2x+3,即x
2-3x+1=0.解得
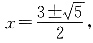
又因为点P在对称轴右侧的抛物线上,所以
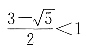
(舍去)所以

所以
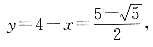
即点P坐标为

②若以CD为一腰,因为点P在对称轴右侧的抛物线上,所以只可能有CD=PD,由抛物线对称性知,点P与点C关于直线x=1对称,此时点P坐标为(2,3).
所以由①②可知符合条件的点P坐标为
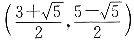
或(2,3).
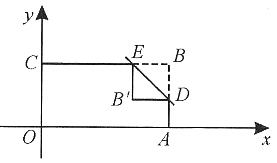
10. 若点M是抛物线上一点,以B、C、D、M为顶点的四边形是直角梯形,试求出点M的坐标.
解:由B(3,0),C(0,3),D(1,4),根据两点间距离公式,得
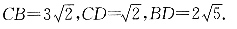
所以CD
2+CB
2=BD
2,所以∠BCD=90°.
设对称轴交x轴于点E,过C作CM⊥DE,交抛物线于点M,垂足为F,在Rt△DCF中,因为CF=DF=1,所∠CDF=45°,由抛物线对称性可知,∠CDM=2×45°=90°,所以点M的坐标为(2,3).所以DM//BC,所以四边形BCDM为直角梯形.
由∠BCD=90°及题意可知,以BC为一底时,顶点M在抛物线上的直角梯形只有上述一种情况;以CD为一底或以BD为一底,且顶点M在抛物线上的直角梯形均不存在.
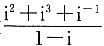 等于______.
等于______.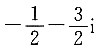
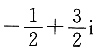
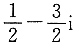
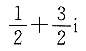
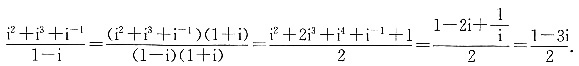
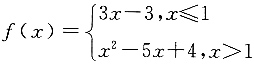 的图象和函数g(x)=log2x的图象的交点个数是______.
的图象和函数g(x)=log2x的图象的交点个数是______.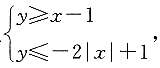 所表示的平面区域的面积为______.
所表示的平面区域的面积为______.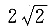
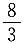
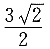
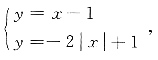 解得
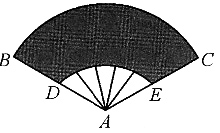
解得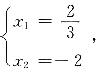 不等组表示的平面区域面积为
不等组表示的平面区域面积为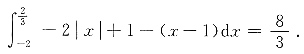
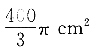
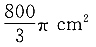
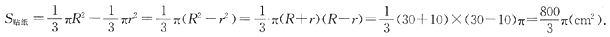
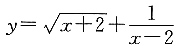 中,自变量x的取值范围是______.
中,自变量x的取值范围是______.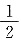 ∠B+
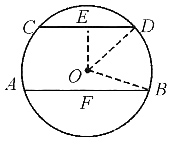
∠B+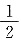 ∠C=180°,故∠BOC=180°-
∠C=180°,故∠BOC=180°-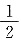 (∠B+∠C)=115°.
(∠B+∠C)=115°.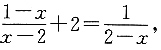 可知方程______.
可知方程______.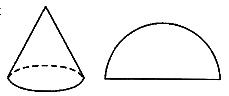
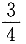
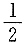
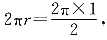 解得
解得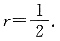
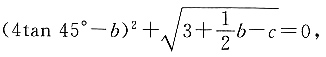 以a,b,c为边长组成的三角形面积等于______.
以a,b,c为边长组成的三角形面积等于______.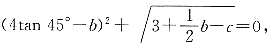 所以4tan 45°-b=0,3+
所以4tan 45°-b=0,3+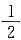 b-c=0,所以b=4,c=5.又因为a2+b2=9+16=25=c2,所以△ABC是直角三角形,且a,b为两条直角边,所以△ABC的面积
b-c=0,所以b=4,c=5.又因为a2+b2=9+16=25=c2,所以△ABC是直角三角形,且a,b为两条直角边,所以△ABC的面积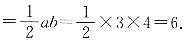 故选A.
故选A.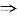 4+6-5m=0
4+6-5m=0 m=2.
m=2.
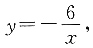 当x=-2时,y的值是______.
当x=-2时,y的值是______.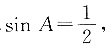 则∠A=______.
则∠A=______. 所以∠A=30°.
所以∠A=30°.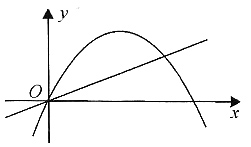
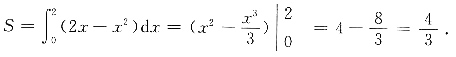
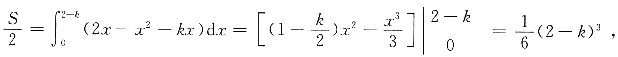
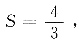 所以(2-k)3=4,则
所以(2-k)3=4,则
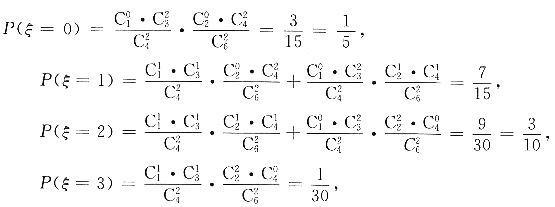


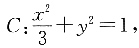 设直线l与椭圆C交于A、B两点,坐标原点O到直线l的距离为
设直线l与椭圆C交于A、B两点,坐标原点O到直线l的距离为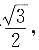 |AB|的最大值.
|AB|的最大值.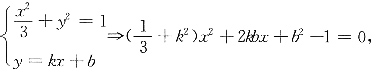
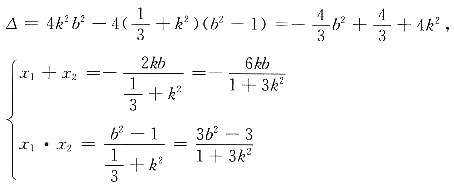
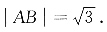
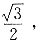 所以
所以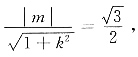 得到
得到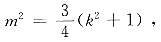
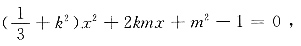
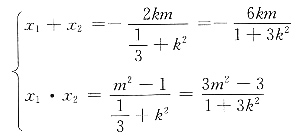
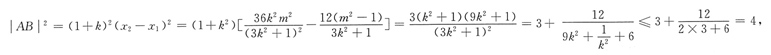
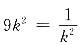 时,|AB|2取最大值4,则|AB|最大值为2.
时,|AB|2取最大值4,则|AB|最大值为2.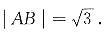
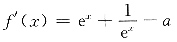
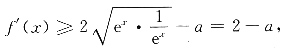 即f'(x)最小值为2-a.
即f'(x)最小值为2-a.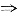 ex+e-x≥a,又因为ex+e-x≥2,所以a≤2.
ex+e-x≥a,又因为ex+e-x≥2,所以a≤2.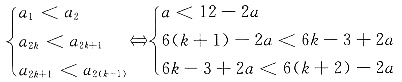
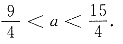
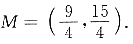

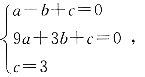
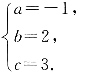
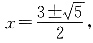 又因为点P在对称轴右侧的抛物线上,所以
又因为点P在对称轴右侧的抛物线上,所以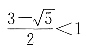 (舍去)所以
(舍去)所以
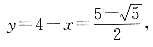 即点P坐标为
即点P坐标为
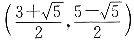 或(2,3).
或(2,3).