第一部分 客观题7. 已知a>0,b>0,则

的最小值为______.
A.2
B.

C.4
D.5
A B C D
C
[解析] 已知a>0,b>0,因此

则

当且仅当a=b时,“=”成立,于是

当且仅当

即a=b=1时,“=”成立.故当a=b=1时,原式的最小值为4.
10. 已知复数z=z+yi,z,y∈R,i为虚数单位,则下列表达式中正确的是______.
A.
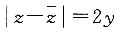
B.|z|≤|x|+|y|
C.
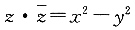
D.z
2=x
2+y
2 A B C D
B
[解析] 由题意得z=x+yi,则

=z-yi,A项,|z-

|=|2y|≥2y,故A项错误;B项,

故B项正确;C项,

=(x+yi)(x-yi)=x
2+y
2,故C项错误;D项,z
2=x
2-y
2+2xyi,故D项错误,因此答案为B.
12. 已知函数
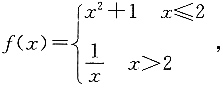
则f(f(2))=______.
A.
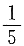
B.5
C.26
D.
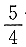
A B C D
A
[解析] 由题可知,f(2)=2
2+1=5,则f(f(2))=f(5)=

,故答案为A.
15. 抛物线y
2=x的焦点到准线的距离为______.
A.
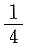
B.

C.1
D.2
A B C D
B
[解析] 南题意可知抛物线方程为y
2=x,则

因此抛物线焦点到准线的距离为

答案为B.
16. 一个样本中有五个数据,分别为a,1,2,3,5.若该样本的平均值为2,则样本的方差为______.
A.16
B.4
C.2
D.

A B C D
B
[解析] 由题意可知,

解得a=-1,则样本方差为S
2=

(-1-2)
2+(1-2)
2+(2-2)
2+(3-2)
2+(5-2)
2]=4.
20. 在(1-2x)
5的展开式中的x
3的系数是______.
A B C D
C
[解析] 二项式(1-2x)
5展开式的通项公式为

令r=3,则x
3的系数为

故答案为C.
21. 已知{a
n}(n∈N
*)为等差数列,其前n项和为S
n且满足a
1=-13,a
4+a
6=-10,则当S
n取得最小值时,n为______.
A B C D
B
[解析] 设数列的公差为d,因为a1=-13,又a1+a6=2a1+8d=-10,解得d=2,则Sn=-13n+n(n-1)=(n-7)2-49,因此当n=7时,Sn有最小值.
22. 已知某数列{a
n}(n∈N
*)的首项a
1≠0,记其前n项和为S
n若满足等式S
n+1=2S
n+a
1,则
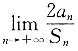
=______.
A.0
B.
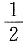
C.1
D.2
A B C D
C
[解析] 由题S
n+1=2S
n+a
1①可知S
n=2S
n-1+a
1②,则①-②得a
n+1=2a
n数列{a
n}是首项为a
1,公比q为2的等比数列,则

23. 在△ABC中,M是BC的中点,AM=1,点P在AM上,且满足
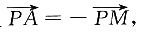
求
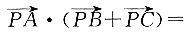
______.
A.-2
B.
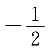
C.
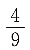
D.2
A B C D
B
[解析] 因为AM=1,点P在AM上且

,因此

又

则
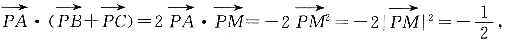
答案为B.
24. 向量a的模|a|=1,向量b的模|b|=2,且满足
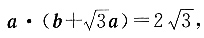
则向量a与向量b的夹角为______.
A.
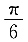
B.
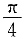
C.
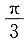
D.
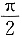
A B C D
A
[解析] 由题可知

|a|=1,|b|=2,因为a·(b+

)=|a||b|cos<a,b>+

=2cos<a,b>+

×1
2=

解得

因为夹角θ∈[0,π],故向量a,b的夹角为

答案为A.
25. 已知等比数列{a
n)中,a
2=1,且公比q<0,则其前三项的和S
3的取值范围是______.
- A.(-∞,-1]
- B.(-∞,0)∪(1,+∞)
- C.[3,+∞)
- D.(-∞,-1]∪[3,+∞)
A B C D
A
[解析] 由已知a
2=1,得S
3=a
1+a
2+a
3=

+1+q,又q<0,
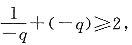
当且仅当q=-1时,“=”成立,所以

所以S
3≤-1,因此答案为A.
27. 若函数

x∈[0,π],则f(x)的值域为______.
A.[-2,2]
B.
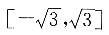
C.[-1,1]
D.

A B C D
D
[解析] 函数

又x∈[0,π]即
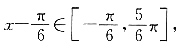
所以
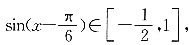
故函数f(x)的值域为

28. 若将函数f(x)=sinωx向右移动

个单位后的函数过定点
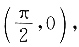
则ω的最小值可以是______.
A.

B.4
C.

D.2
A B C D
B
[解析] 由题可知,函数f(x)=sinωx向右移动
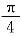
个单位后变为
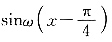
其经过点
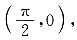
即

因此ω的最小值为4.
29. 下列函数中,在区间

上单调递减,且周期为π的函数是______.
A.

B.

C.

D.

A B C D
A
[解析] 由
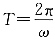
可知A项和B项的函数周期为π,又因为在区间
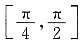
上,
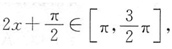
函数
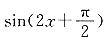
单调递减,函数
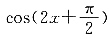
单调递增,因此答案为A.
30.

______.
A.

B.1
C.
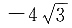
D.

A B C D
C
[解析]

34. 设三棱柱的侧棱垂直于底面,所有棱长都为a,顶点都在一个球面上,则该球的表面积为______.
A.πa
2 B.5πa
2 C.
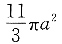
D.

A B C D
D
[解析] 由题可知三棱柱是棱长都为a的正三棱柱,上下底面中心连线的中点就是球心,则其外接球的半径为

则球的表面积为
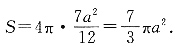
故答案为D.
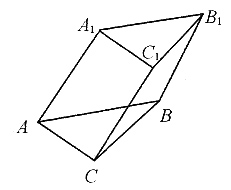
35. 在三棱柱ABC-A
1B
1C
1中,∠ACB=90°,∠ACC
1=60°,∠BCC
1=45°,侧棱CC
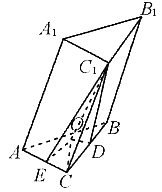
1的长为1,则该三棱柱的高是多少______.
A.

B.1
C.
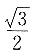
D.
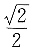
A B C D
A
[解析] 如下图,过点C
1作C
1O上平面ACB于O,C
1E⊥AC于E,C
1D⊥CB于D,因此OE⊥AC,OD⊥CB,又∠ACB=90°,则四边形ECDO为矩形,CE=DO,又CC
1=1,在Rt△C
1EC中,∠ECC
1=60°,则

在Rt△C
1DC中,∠C
1CD=45°,则

因此三棱柱的高为
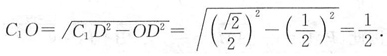
36. 三棱柱ABC-A
1B
1C
1各棱长相等,侧棱垂直于底面,点D是侧面BB
1C
1C的中心,求AD与平面BB
1C
1C所成的角______.
A B C D
A
[解析] 如下图,过D点作DE⊥BC于E,连接AE,所以AE⊥DE,则∠ADE为AD与平面BB
1C
1C所成的角.设各棱长为1,因为BB
1C
1C是正方形,则

又

则AD=1,因此∠ADE=60°,故AD与平面BB
1C
1C所成的角为60°.

39. 从2,3,4,5,6中取两个不同的数,事件A=“取到的两个数之和为偶数”,事件B=“取到的两个数都为偶数”,则P(B|A)=______.
A.
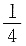
B.
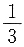
C.
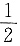
D.

A B C D
D
[解析] 由题可知,

因此
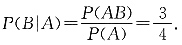
41. 双曲线的一个端点到两焦点的距离比为
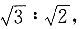
则双曲线的离心率为______.
A.

B.
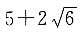
C.
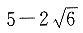
D.

A B C D
C
[解析] 由题双曲线一个端点到两焦点的距离比为
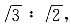
设这一端点到两焦点的距离为
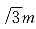
和

,则
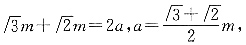
因此

故

43.

取得最值时的坐标为______.
A.
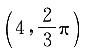
B.
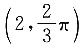
C.
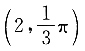
D.
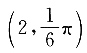
A B C D
A
[解析]
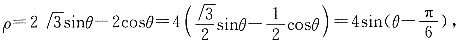
因此,当
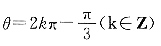
时,ρ
min=-4;当
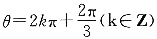
时,ρ
max=4.将四个选项逐一代入,可知A项符合题意.
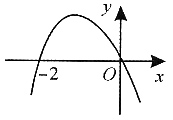
45. 若对任意的使不等式组

成立的实数x,y都能使不等式x-2y+m≤0成立,则实数m的取值范围是______.
A.0≤m≤1
B.1≤m≤3
C.m≤0
D.
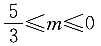
A B C D
C
[解析] 由已知可画出图形,如图所示,图中阴影部分为不等式组所确定的实数x,y的取值范围.若想对于所取任意实数x,y均能使x-2y+m≤0成立,则在图象中,阴影部分全部在直线x-2y+m=0的图象的上半部分,故当x-2y+m=0过A点时,m有最大值.由

可得,
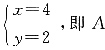
的坐标为(4,2),将其代入直线x-2y+m=0,可得m=0,所以m的取值范围为m≤0.
47. 直线y=x+b与曲线

有公共点,则b的取值范围是______.
A.[-3,-1]
B.

C.
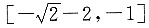
D.
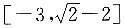
A B C D
C
[解析] 由题可知,曲线
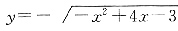
表示圆(x-2)
2+y
2=1的下半圆,如下图所示,直线交圆于点(1,0)时,b=-1;直线与圆相切时,即点(2,0)到直线的距离为1,
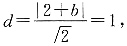
则

(舍)或

因此若直线y=x+b与圆有交点,b的取值范围为
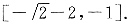
49. 下列为无穷小的是______.
A.
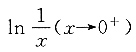
B.lnx(x→1)
C.cosx(x→0)
D.
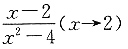
A B C D
B
[解析] 因为
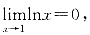
所以函数lnx是当x→1时的无穷小.
52. y=x
3-2x
2-x+2与x轴所围成的平面图形的面积为______.
A.
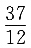
B.
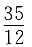
C.
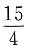
D.
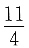
A B C D
A
[解析] 由已知得,曲线与x轴的交点为-1,1,2,图象先增后减再增,在区间(-1,1)上,曲线在x轴上方,在区间(1,2)上.曲线在x轴下方,因此曲线与x轴围成的平面图形面积
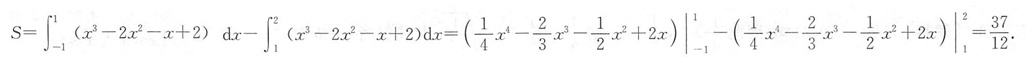
59. 设函数f(x)=ax
3+3x
2,若

则f(x)的拐点为______.
A.(a,3)
B.(-4,8)
C.(-1,1)
D.
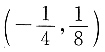
A B C D
D
[解析] 因为
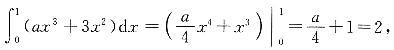
即a=4,所以f(x)=4x
3+3x
2,所以f'(x)-12x
2+6x,f''(x)=24x+6.f''(x)=0.即

所以该曲线的拐点为
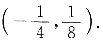
第二部分 主观题1. 求过点(2,-1,4)、(-1,3,-2)、(0,2,3)的平面方程.
解:设平面方程为Ax+By+Cz+D=0,将三点坐标代入得
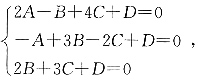
解得平面方程为14x+9y-z-15=0.
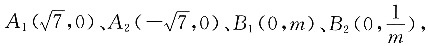 A1B1与A2B2交于点N,点N的轨迹为曲线C.
A1B1与A2B2交于点N,点N的轨迹为曲线C.2. 求C的函数表达式;
解:设N点坐标为(x,y),
则直线A
1B
1的斜率为
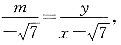
直线A
2B
2的斜率为
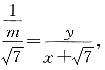
因此
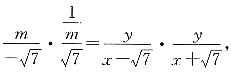
得到曲线C的轨迹方程为
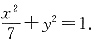
3. 过点

的直线l交曲线C于P、Q两点,若以PQ为直径的圆与y轴相切,求直线l的方程.
解:设直线l的方程为

与椭圆C联立得,
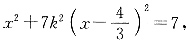
整理得,

设P(x
1,y
1),Q(x
2,y
2)
所以
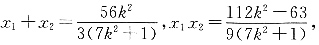
因为以PQ为直径的圆与y轴相切,
所以
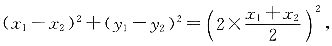
整理得
k
2(x
1+x
2)
2-4(k
2+1)x
1x
2=0,
将
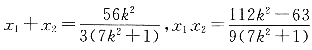
代入解得,k
2=1,即k=±1,
所以直线l的方程为3x-3y-4=0或3x+3y-4=0.

4. 讨论f(x)的单调性;
解:因为
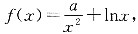
则函数的定义域为x∈(0,+∞),

若a≤0,必有f'(x)>0,即f(x)在定义域x∈(0,+∞)上为单调递增函数;
若a>0,当f'(x)≥0,即
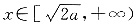
时,f(x)为单调递增函数,当f'(x)≤0,即
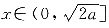
时,f(x)为单调递减函数.
5. 若对任意的
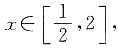
有xf(x)≥1,求a的取值范围.
解:当

时,因为
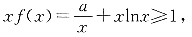
故a≥x-x
2lnx,
令g(x)=x-x
2lnx,则g'(x)=1-2xlnx-x,
令g'(x)=0,即1-2xlnx-x=0,整理得,
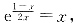
解得x=1,
即当x=1时,g(x)
max=x-x
2lnx=1-1
2·lnl=1
所以a≥g(x)
max=1,即a≥1.
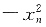 +xn+c,n∈N*,求{xn}是递增数列时c的取值范围.
+xn+c,n∈N*,求{xn}是递增数列时c的取值范围.
板书设计如下:
假设{xn)是递增数列,x1=0得,x2=c,x3=-c2+2c,
由x1<x2<x3得,0<c<1,
由xn<xn+1=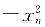 +xn+c知
+xn+c知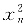 <c,即对任意的n≥1有
<c,即对任意的n≥1有
注意到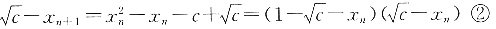
由①和②可得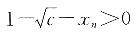 即
即
由②和xn≥0还可得,对任意n≥1都有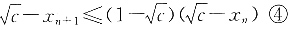
反复运用④得
将③和⑤相加得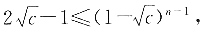 知对任意n≥1成立.
知对任意n≥1成立.
根据指数函数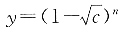 的性质,得
的性质,得
故c的取值范围是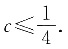
6. 你认为上述解答是否完善,若不完善,请进行补充。
不完善的地方有:①未综合前后c的范围,结果应为
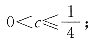
②只证明了充分性,未证明必要性(证明过程略);
7. 分析隐含的数学思想方法,并根据该思想方法写出教学目标.
本题隐含了抽象与推理、转化与化归、数列与函数等数学思想方法.
教学目标:巩固数列的概念及其性质,灵活运用不等式及其性质,理解充要条件的意义.
 的最小值为______.
的最小值为______.
 则
则 当且仅当a=b时,“=”成立,于是
当且仅当a=b时,“=”成立,于是 当且仅当
当且仅当 即a=b=1时,“=”成立.故当a=b=1时,原式的最小值为4.
即a=b=1时,“=”成立.故当a=b=1时,原式的最小值为4.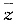 ,i为虚数单位,若z=1+i,则(z-1)(
,i为虚数单位,若z=1+i,则(z-1)(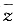 +1)=______.
+1)=______.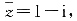 因此(z-1)(
因此(z-1)(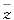 +1)=(1+i-1)(1-i+1)=1+2i.
+1)=(1+i-1)(1-i+1)=1+2i.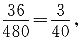 故从各层中抽取的人数分别是
故从各层中抽取的人数分别是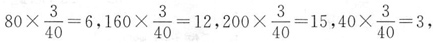 答案为C.
答案为C.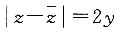
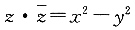
 =z-yi,A项,|z-
=z-yi,A项,|z- |=|2y|≥2y,故A项错误;B项,
|=|2y|≥2y,故A项错误;B项, 故B项正确;C项,
故B项正确;C项, =(x+yi)(x-yi)=x2+y2,故C项错误;D项,z2=x2-y2+2xyi,故D项错误,因此答案为B.
=(x+yi)(x-yi)=x2+y2,故C项错误;D项,z2=x2-y2+2xyi,故D项错误,因此答案为B.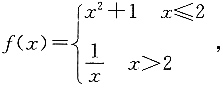 则f(f(2))=______.
则f(f(2))=______.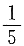
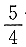
 ,故答案为A.
,故答案为A.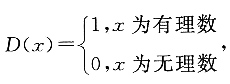 则下列结论错误的是______.
则下列结论错误的是______.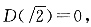 D(2)=1,所以D(x)不是单调函数,D项正确.故答案为A.
D(2)=1,所以D(x)不是单调函数,D项正确.故答案为A.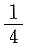

 因此抛物线焦点到准线的距离为
因此抛物线焦点到准线的距离为 答案为B.
答案为B.
 解得a=-1,则样本方差为S2=
解得a=-1,则样本方差为S2= (-1-2)2+(1-2)2+(2-2)2+(3-2)2+(5-2)2]=4.
(-1-2)2+(1-2)2+(2-2)2+(3-2)2+(5-2)2]=4.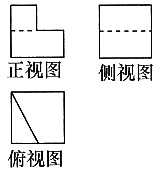
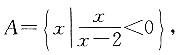 集合B={x||x-2|<1},则“m∈A”是“m∈B”的______.
集合B={x||x-2|<1},则“m∈A”是“m∈B”的______. 令r=3,则x3的系数为
令r=3,则x3的系数为 故答案为C.
故答案为C.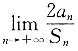 =______.
=______.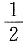

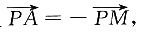 求
求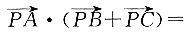 ______.
______.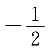
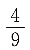
 ,因此
,因此 又
又 则
则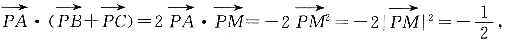 答案为B.
答案为B.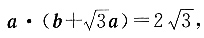 则向量a与向量b的夹角为______.
则向量a与向量b的夹角为______.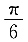
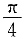
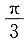
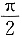
 |a|=1,|b|=2,因为a·(b+
|a|=1,|b|=2,因为a·(b+ )=|a||b|cos<a,b>+
)=|a||b|cos<a,b>+ =2cos<a,b>+
=2cos<a,b>+ ×12=
×12= 解得
解得 因为夹角θ∈[0,π],故向量a,b的夹角为
因为夹角θ∈[0,π],故向量a,b的夹角为 答案为A.
答案为A. +1+q,又q<0,
+1+q,又q<0,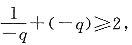 当且仅当q=-1时,“=”成立,所以
当且仅当q=-1时,“=”成立,所以 所以S3≤-1,因此答案为A.
所以S3≤-1,因此答案为A.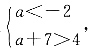 解得-3<a<-2,因此答案为C.
解得-3<a<-2,因此答案为C. x∈[0,π],则f(x)的值域为______.
x∈[0,π],则f(x)的值域为______.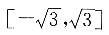

 又x∈[0,π]即
又x∈[0,π]即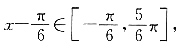 所以
所以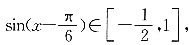 故函数f(x)的值域为
故函数f(x)的值域为
 个单位后的函数过定点
个单位后的函数过定点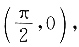 则ω的最小值可以是______.
则ω的最小值可以是______.

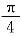 个单位后变为
个单位后变为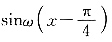 其经过点
其经过点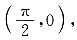 即
即 因此ω的最小值为4.
因此ω的最小值为4. 上单调递减,且周期为π的函数是______.
上单调递减,且周期为π的函数是______.



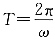 可知A项和B项的函数周期为π,又因为在区间
可知A项和B项的函数周期为π,又因为在区间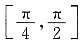 上,
上,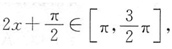 函数
函数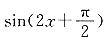 单调递减,函数
单调递减,函数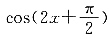 单调递增,因此答案为A.
单调递增,因此答案为A. ______.
______.
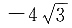


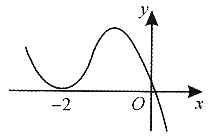
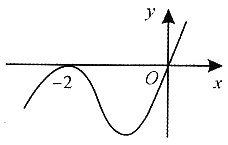
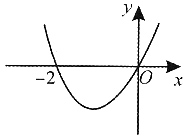
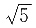

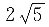
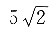
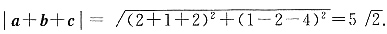
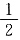 -0.023=0.477.
-0.023=0.477.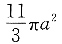

 则球的表面积为
则球的表面积为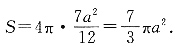 故答案为D.
故答案为D.

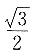
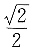
 在Rt△C1DC中,∠C1CD=45°,则
在Rt△C1DC中,∠C1CD=45°,则 因此三棱柱的高为
因此三棱柱的高为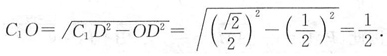

 又
又 则AD=1,因此∠ADE=60°,故AD与平面BB1C1C所成的角为60°.
则AD=1,因此∠ADE=60°,故AD与平面BB1C1C所成的角为60°.
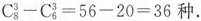
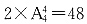 种,一共有2×48=96种;又因仅有中间行的数字之和为8,即上下两行中,每行两数字之和都不能为8,故还需减去其他行存在两数字之和为8的情况,所以所求的排法确
种,一共有2×48=96种;又因仅有中间行的数字之和为8,即上下两行中,每行两数字之和都不能为8,故还需减去其他行存在两数字之和为8的情况,所以所求的排法确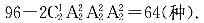
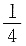
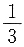
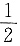

 因此
因此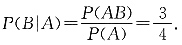
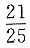
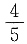
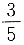
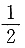
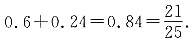
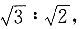 则双曲线的离心率为______.
则双曲线的离心率为______.
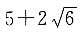
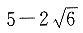

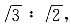 设这一端点到两焦点的距离为
设这一端点到两焦点的距离为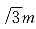 和
和 ,则
,则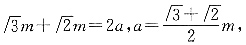 因此
因此 故
故
 取得最值时的坐标为______.
取得最值时的坐标为______.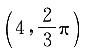
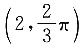
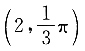
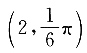
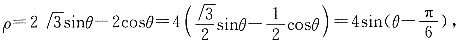 因此,当
因此,当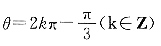 时,ρmin=-4;当
时,ρmin=-4;当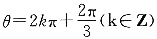 时,ρmax=4.将四个选项逐一代入,可知A项符合题意.
时,ρmax=4.将四个选项逐一代入,可知A项符合题意. 成立的实数x,y都能使不等式x-2y+m≤0成立,则实数m的取值范围是______.
成立的实数x,y都能使不等式x-2y+m≤0成立,则实数m的取值范围是______.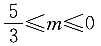
 可得,
可得,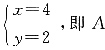 的坐标为(4,2),将其代入直线x-2y+m=0,可得m=0,所以m的取值范围为m≤0.
的坐标为(4,2),将其代入直线x-2y+m=0,可得m=0,所以m的取值范围为m≤0. 有公共点,则b的取值范围是______.
有公共点,则b的取值范围是______.
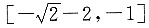
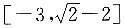
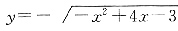 表示圆(x-2)2+y2=1的下半圆,如下图所示,直线交圆于点(1,0)时,b=-1;直线与圆相切时,即点(2,0)到直线的距离为1,
表示圆(x-2)2+y2=1的下半圆,如下图所示,直线交圆于点(1,0)时,b=-1;直线与圆相切时,即点(2,0)到直线的距离为1,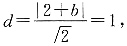 则
则 (舍)或
(舍)或 因此若直线y=x+b与圆有交点,b的取值范围为
因此若直线y=x+b与圆有交点,b的取值范围为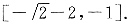

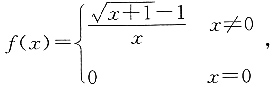 则x=0是______.
则x=0是______.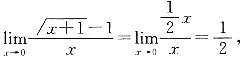 又f(0)=0,所以x=0是函数的可去间断点.
又f(0)=0,所以x=0是函数的可去间断点.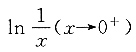
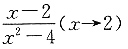
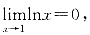 所以函数lnx是当x→1时的无穷小.
所以函数lnx是当x→1时的无穷小.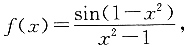 则______.
则______.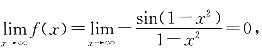 因此y=0是曲线的渐近线.
因此y=0是曲线的渐近线.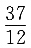
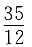
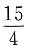
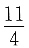
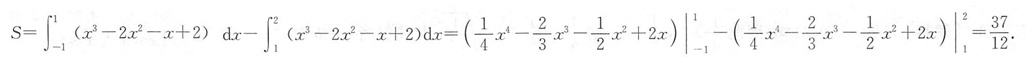
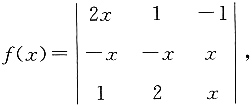 则x3的系数为______.
则x3的系数为______.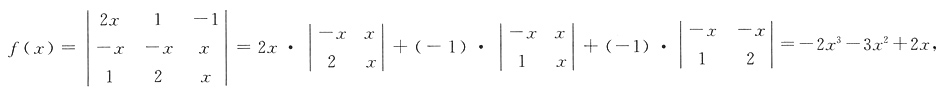 因此x3的系数为-2.
因此x3的系数为-2.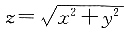 可以由______.
可以由______.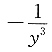
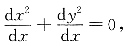 即
即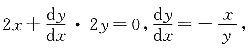 则
则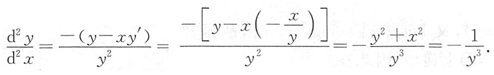
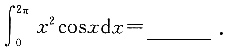
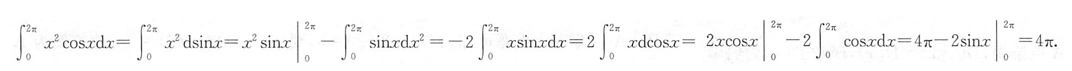
 又因为f''(x)>0,则函数f'(x)在[0,1]上单调递增,而0<ξ<1,故f'(0)<f'(ξ)<f'(1),即f'(0)<f(1)-f(0)<f'(1).
又因为f''(x)>0,则函数f'(x)在[0,1]上单调递增,而0<ξ<1,故f'(0)<f'(ξ)<f'(1),即f'(0)<f(1)-f(0)<f'(1). 则f(x)的拐点为______.
则f(x)的拐点为______.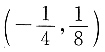
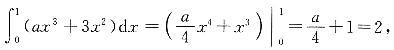 即a=4,所以f(x)=4x3+3x2,所以f'(x)-12x2+6x,f''(x)=24x+6.f''(x)=0.即
即a=4,所以f(x)=4x3+3x2,所以f'(x)-12x2+6x,f''(x)=24x+6.f''(x)=0.即 所以该曲线的拐点为
所以该曲线的拐点为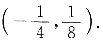
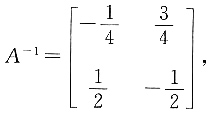 则A的特征值为______.
则A的特征值为______.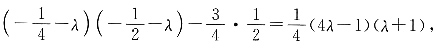 因此A-1的特征值为
因此A-1的特征值为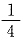 和-1,则A的特征值为4和-1.答案为D.
和-1,则A的特征值为4和-1.答案为D.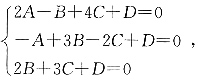 解得平面方程为14x+9y-z-15=0.
解得平面方程为14x+9y-z-15=0.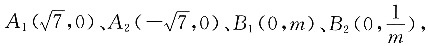 A1B1与A2B2交于点N,点N的轨迹为曲线C.
A1B1与A2B2交于点N,点N的轨迹为曲线C.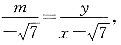
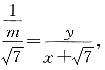
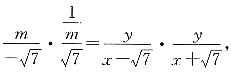 得到曲线C的轨迹方程为
得到曲线C的轨迹方程为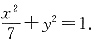
 的直线l交曲线C于P、Q两点,若以PQ为直径的圆与y轴相切,求直线l的方程.
的直线l交曲线C于P、Q两点,若以PQ为直径的圆与y轴相切,求直线l的方程. 与椭圆C联立得,
与椭圆C联立得,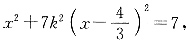 整理得,
整理得,
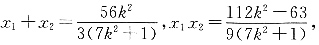
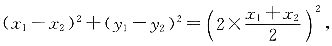 整理得
整理得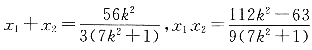 代入解得,k2=1,即k=±1,
代入解得,k2=1,即k=±1,
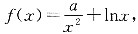 则函数的定义域为x∈(0,+∞),
则函数的定义域为x∈(0,+∞),
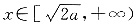 时,f(x)为单调递增函数,当f'(x)≤0,即
时,f(x)为单调递增函数,当f'(x)≤0,即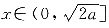 时,f(x)为单调递减函数.
时,f(x)为单调递减函数.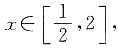 有xf(x)≥1,求a的取值范围.
有xf(x)≥1,求a的取值范围. 时,因为
时,因为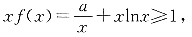
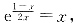 解得x=1,
解得x=1,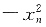 +xn+c,n∈N*,求{xn}是递增数列时c的取值范围.
+xn+c,n∈N*,求{xn}是递增数列时c的取值范围.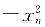 +xn+c知
+xn+c知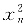 <c,即对任意的n≥1有
<c,即对任意的n≥1有
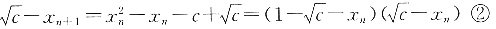
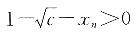 即
即
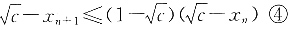

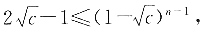 知对任意n≥1成立.
知对任意n≥1成立.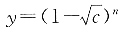 的性质,得
的性质,得
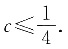
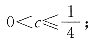 ②只证明了充分性,未证明必要性(证明过程略);
②只证明了充分性,未证明必要性(证明过程略);