一、1. 一半径等于3mm的导体球,处于ε
r=2.5的介质中,已知距离球心2m处的电场强度为1mV/m,求导体球上的电荷。
由对称性可知,该导体球引起的电场只与r有关。由介质中的高斯定理,有:
E·ε
0ε
r·4πr
2=Q
则可得:Q=10
-3ε
0×2.5×4π×4=0.04πε
0 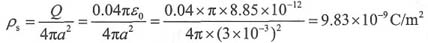
(导体电荷只能分布在表面)
二、1. 矢量E=(yz-3x)e
x+xze
y+xye
z是否可能是静电场的解?如果是,则求与之对应的源和电位。
若是静电场的解,应满足
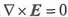
,因此:
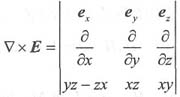
所以 e
x(x-x)+e
y(y-y)+e
z(z-z)=0
则矢量E是静电场的解。
对应的源:
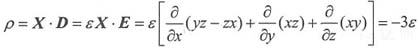
由E=-X·ρ可得:
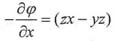
则有:
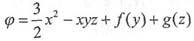
因有:
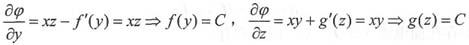
所以:
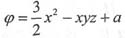
(a为常数)
三、1. 如下图所示,假设同轴线内、外导体半径分别为a和b,内、外导体间填充μ
1、μ
2两种介质,并各占一半的空间,求内、外导体间的磁场强度。
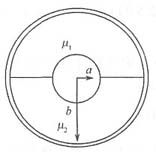
设同轴线中通过的电流为I,同轴线的内、外导体之间的磁场沿
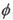
方向。在两种介质的分界面上,只有法向分量,根据边界条件,B的法向分量连续,即:
B
1=B
2=e
ρB
利用安培环路定律,有πρ(H
1+H
2)=I,即:
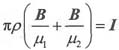
则可得:
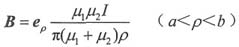
因此有:
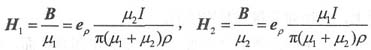
四、1. 从麦克斯韦方程出发,导出两不同介质的边界条件。
(1)H的边界条件。如下图所示为两种介质的分界面,1区介质的参数为μ
1、ε
1和σ
1;2区介质的参数为μ
2、ε
2和σ
2。
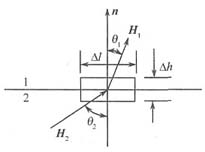
在分界面上取一个无限靠近分界面的无穷小矩形闭合路径,并使两边落在分界面的两侧,若取小矩形闭合回路的边长为无穷小量Δh→0,宽为高阶无穷小量Δl。且小矩形闭合回路围成的面元的方向为a
s。设分界面单位法向矢量为n,分界面上面电流密度为J
s,将积分形式的麦克斯韦第一方程式应用于此矩形闭合回路,忽略高阶无穷小量时可得:
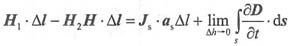
因此有:
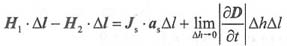
对于实际的电磁场,场量随时间是连续变化的,则
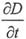
是有限量,当Δh→0时,
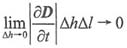
。而Δl=a
s×nΔl,于是得:
(H
1-H
2)·a
s×nΔl=J
s·a
sΔl
经过简单的矢量混合积变换得:n×(H
1-H
2)·a
sΔl=J
s·a
sΔl
由于小矩形闭合回路的选取具有任意性,则可得:
n×(H
1-H
2)=J
s 若分界面上不存在面电流(即J
s=0)时,则有:
n×(H
1-H
2)=0
由此可见,当分界面上分布有源面电流时,H从一种介质进入另一种介质时,其切向分量会发生突变,其突变量就等于分界面上的面电流密度。若分界面上没有面电流,则H的切向分量是连续的。
(2)E的边界条件。将麦克斯韦第二方程的积分形式用于如下图所示的无穷小矩形闭合回路,可得
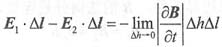
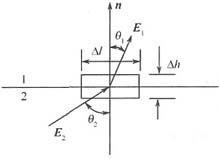
式中,
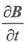
是有限量,当Δh→0时,
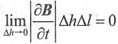
,可得:
(E
1-E
2)·a
s×nΔl=0
即:n×(E
1-E
2)=0
说明E在分界面上,其切向分量总是连续的。
(3)B的边界条件。存不同介质的分界面上取一小扁形闭合柱面,如下图所示。
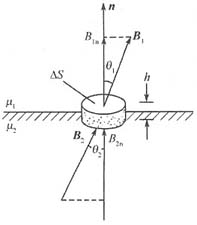
将麦克斯韦第三方程的积分式应用于此闭合面可得:

因此可得n·(B
1-B
2)=0,即:B
1n-B
2n=0
这说明B在分界面上的法向分量总是连续的。
(4)D的边界条件。将麦克斯韦第四方程的积分式应用于分界面上所取的一小扁形闭合柱面上可得:
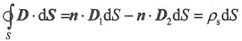
由此可得:n·(D
1-D
2)=ρ
s 若分界面上不存在源面电荷,则:
D
1n-D
2n=0或n·(D
1-D
2)=0
当分界面上存在自由面电荷时,D的法向分量不连续,其增量就等于分界面上自由电荷面密度。若分界面上没有自由面电荷分布,则D的法向分量在分界面上连续。
在不同介质的分界面上的边界条件可归纳为:
分界面上存在源J
s和ρ
s 分界面上无源分布
n×(H
1-H
2)=J
s n×(H
1-H
2)=0
n×(E
1-E
2)=0 n×(E
1-E
2)=0
或者:n·(B
1-B
2)=0 n·(B
1-B
2)=0
n·(D
1-D
2)=ρ
s n·(D
1-D
2)=0
五、1. 写出麦克斯韦方程组的微分形式,由麦克斯韦方程组的两个旋度方程和电荷守恒定律导出两个散度方程。
(1)麦克斯韦方程组的微分形式描述空间任意一点场的变化规律,具体如下:
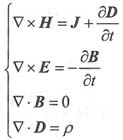
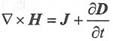
表明时变磁场不仅由传导电流产生,也由位移电流产生,揭示时变电场产生时变磁场;
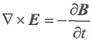
表明时变磁场产生时变电场;
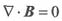
表明磁通永远是连续的,磁场是无散度场;
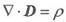
表明空间任意点的若有电荷存在,电位移线在该点发出或汇聚。
(2)麦克斯韦方程组的两个旋度方程为:
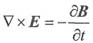
①
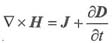
②
对①式求散度:
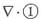
:已知
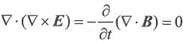
设

,相对时间t而言是常数,由初始条件确定。
假设初始时刻B=0或B=常矢(稳恒场)则:
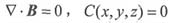
对②式求散度
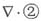
。设:
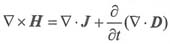
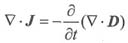
由电荷守恒定律

,得散度方程:
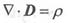
上述推导即为波动方程的推导。
对①式两边求旋度,可得:
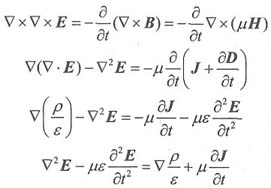
以上推导中利用了矢量恒等式及其
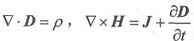
。
同理可推出关于磁场满足的方程:
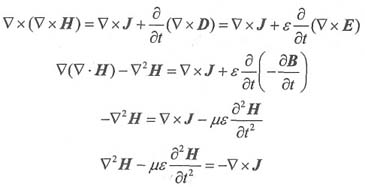
九、1. 证明任意一个线极化波可以分解为两个幅度相同、旋向相反的圆极化波。
证明:已知线极化波的电场可以写成:

上式可以表示成:
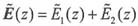
其中
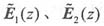
为圆极化波,即:

而且
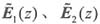
为左右旋的圆极化波。
所以任意一个线极化波可以分解为两个幅度相同、旋向相反的圆极化波。