一、选择题下列每题给出的四个选项中,只有一个选项是符合题目要求的。
1. 当x→0时,下列函数为无穷大量的是______。
A.
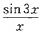
B.cotx
C.
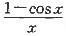
D.
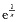
A B C D
B
[解析] 这里采用排除法,
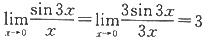
,故排除A;
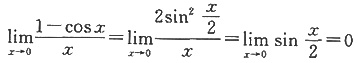
故排除C;当x从负方向趋于0时
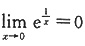
,故排除D,选B。
3. 设

,则______。
A.
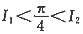
B.
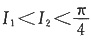
C.
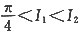
D.
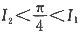
A B C D
A
[解析] 当0<x<
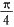
时,sinx<x,故
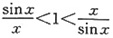
,所以有
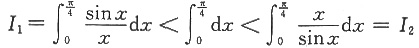
即
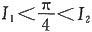
,选A。
4. 设函数z=arctan e
-xy,则dz=______。
A.
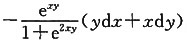
B.
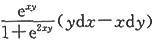
C.
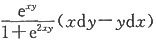
D.
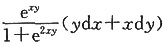
A B C D
A
[解析]
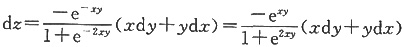
,选A。
5. 将二阶矩阵A的第2列加到第1列得矩阵B,再交换B的第1行与第2行得单位矩阵,则A=______。
A.
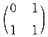
B.
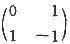
C.
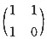
D.
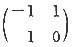
A B C D
D
[解析]
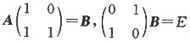
,所以
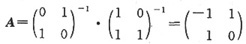
,选D。
6. 设A为4×3矩阵,η
1,η
2,η
3是非齐次线性方程组Ax=β的3个线性无关的解,k
1,k
2为任意常数,则Ax=β的通解为______。
A.
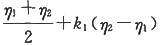
B.
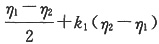
C.
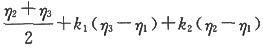
D.
A B C D
C
[解析] 因为η
1,η
2,η
3是Ax=β的线性无关解,所以η
2-η
1,η
3-η
1,是Ax=0的两个线性无关解,而
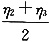
是Ax=β的解,故
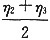
+k
1(η
3-η
1)+k
2(η
2-η
1)是Ax=β的通解,选C。
7. 设随机事件A,B满足A
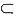
B且0<P(A)<1,则必有______。
A.P(A)≥P(A|A∪B)
B.P(A)≤P(A|A∪B)
C.P(B)≥P(B|A)
D.P(B)≤P(B|
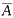
)
A B C D
B
[解析] 因为0<P(A)<1,A
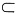
B,故0<P(A)≤P(B)≤1。又A∪B=B,AB=A,所以
P(A|A∪B)=P(A|B)=
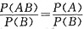
≥P(A),选B。
8. 设总体X服从参数为λ(λ>0)的泊松分布,X
1,X
2,…,X
n(n≥2)为来自总体的简单随机样本,则对于统计量
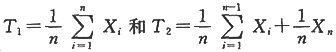
,有______。
- A.ET1>ET2,DT1>DT2
- B.ET1>ET2,DT1<DT2
- C.ET1<ET2,DT1<DT2
- D.ET1<ET2,DT1<DT2
A B C D
D
[解析] 因为X
1,X
2,…,X
n是来自参数为λ的泊松分布的简单随机样本,则有
E(X
1)=E(X
2)=…=E(X
n)=λ,D(X
1)=D(X
2)=…=D(X
n)=λ,那么
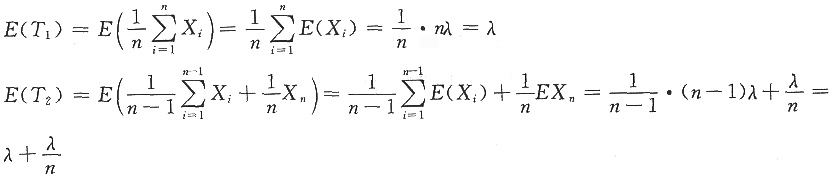
所以E(T
1)<E(T
2)。
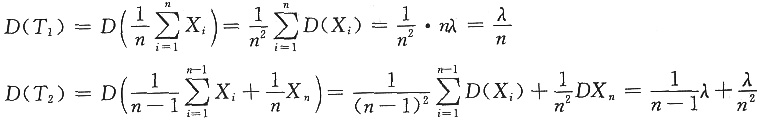
所以D(T
1)<D(T
2)。
选D。
二、填空题1. 设函数
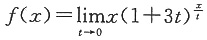
,则f'(x)=______。
(1+3x)e3x
[解析]
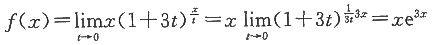
f'(x)=e
3x+3xe
3x=(1+3x)e
3x。
2. 曲线y=x
3-3x
2+3x+1在其拐点处的切线方程是______。
y=2
[解析] y'=3x
2-6x+3,y"=6x-6,
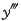
=6,所以点(1,2)为曲线的拐点,而y'(1)=0,所以y=2为拐点处的切线方程。
3. 反常积分
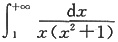
=______。
[解析]
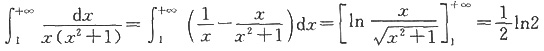
。
4. 设函数z=(2x+y)
3xy,则
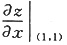
=______。
27(2+3ln3)
[解析]
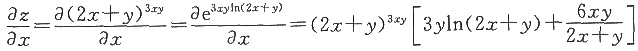
所以
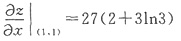
5. 设矩阵
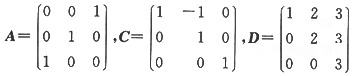
且3阶矩阵B满足ABC=D,则|B
-1|=______。
[解析] 因为|A|=-1,|B|=1,|C|=6,|ABC|=|D|,故
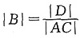
,所以
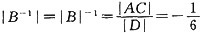
。
6. 设二维随机变量(X,Y)服从正态分布N(μ,μ,σ
2,σ
2,0),则E(XY
2)=______。
μ(σ2+μ2)
[解析] 因为ρ=0,故X与Y相互独立,即有E(XY2)=EXE(Y2)=μE(Y2),而Y~N(μ,σ2),所以DY=E(Y2)-(EY)2,即
E(Y2)=DY+(EY)2=σ2+μ2,故E(XY2)=μ(σ2+μ2)。
三、解答题解答应写出文字说明、证明过程或演算步骤。
1. 设函数
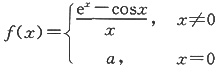
在x=0处连续,求
(Ⅰ)a的值;
(Ⅱ)f'(x)。
(Ⅰ)因为
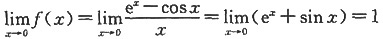
,而f(0)=a,故a=1时f(x)在x=0处连续。
(Ⅱ)当x≠0时,
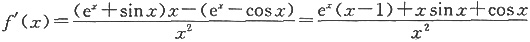
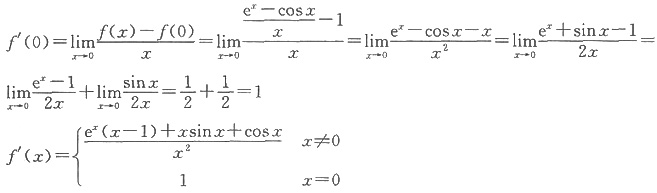
2. 求不定积分
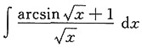
。
3. 设函数y=y(x)是微分方程xdy+(x-2y)dx=0满足条件y(1)=2的解,求曲线y=y(x)与x轴所围图形的面积S。
xdy+(x-2y)dx=0,即

,故
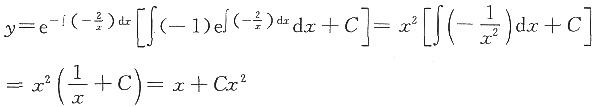
代入初始条件y(1)=2,得C=1,故y=x
2+x。曲线y=x
2+x与X轴交点为(-1,0),(0,0),所以
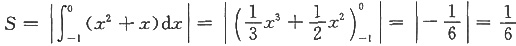
。
4. 证明:当0<x<
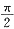
时,
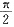
<xsinx+2cosx<2。
证明:令f(x)=xsinx+2cosx,0≤x≤
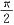
则f'(x)=sinx+xcosx-2sinx=xcosx-sinx
f"(x)=-xsinx+cosx-cosx=-xsinx<0,0<x<
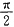
即f'(x)在
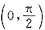
内单调递减,又f'(x)在x=0处连续,故f'(x)<f'(0)<0,即f(x)在
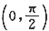
内单调递减,又f(x)在x=0及
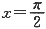
连续,故
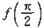
<f(x)<f(0),即
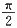
<xsinx+2cosx<2
5. 计算二重积分
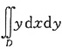
,其中D={(x,y)|x
2+(y-1)
2≤1,x≥0}。
利用极坐标变换,令x=rcosθ,y=rsinθ,则
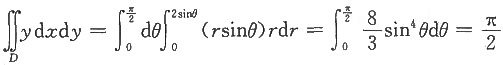
6. 已知α
1=(1,2,1)
T,α
2=(1,1,2)
T,α
3=(1,-1,4)
T,β=(1,0,a)
T,问a为何值时,
(Ⅰ)β不能由α
1,α
2,α
3线性表示;
(Ⅱ)β可由α
1,α
2,α
3线性表示,并写出一般表达式。
β能否由α
1,α
2,α
3线性表示,也就是
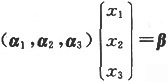
是否有解,而
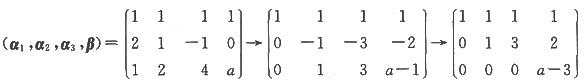
(Ⅰ)当a≠3时,r(α
1,α
2,α
3)≠r(α
1,α
2,α
3,β),方程组
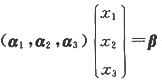
无解,故此时β不能由α
1,α
2,α
3线性表示。
(Ⅱ)当a=3时,r(α
1,α
2,α
3)=r(α
1,α
2,α
3,β)=2,线性方程组
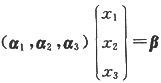
有解,β可由α
1,α
2,α
3线性表示,且因
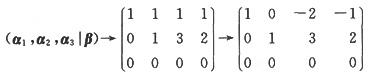
,则
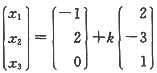
,于是β=(2k-1)α
1+(-3k+2)α
2+kα
3。
7. 已知1是矩阵
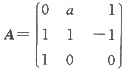
的二重特征值
(Ⅰ)求a的值;
(Ⅱ)求可逆矩阵P和对角矩阵Q,使P
-1AP=Q。
(Ⅰ)1是A的二重特征值,设λ是A的另一个特征值,trA=1+1+λ=0+1+0=1,所以λ=-1,即|-E-A|=0,即
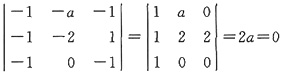
,所以a=0。
(Ⅱ)
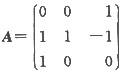
,对于特征值λ=1,有
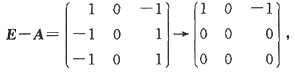
故对应于λ=1的两个线性无关的特征向量
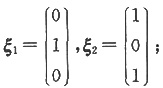
对于λ=-1,有
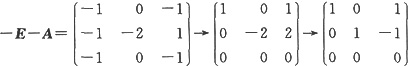
,故对应于λ=-1的特征向量
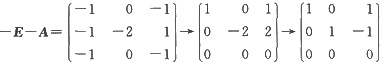
,则有P
-1AP=Q。
8. 设随机变量X与Y的概率分布分别为
| X | 0 | 1 |
| P | 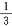 | 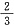 |
且P(X
2=Y
2)=1
(Ⅰ)求二维随机变量(X,Y)的概率分布;
(Ⅱ)求EX,EY及X与Y的相关系数ρ
XY。
(Ⅰ)因为P(X
2=Y
2)=1,所以P(X
2≠Y
2)=1-1=0,则
P(X=1,X
2≠Y
2)=P(X=1,Y=0)=P(X=1|X
2≠Y
2)P(X
2≠Y
2)=0
又P(X=0,X
2≠Y
2)=P(X=0,Y=1)+P(X=0,Y=-1)=0,则
P(X=0,Y=1)=P(X=0,Y=-1)=0
而P(X=0,Y=0)=P(X=0)-P(X=0,Y=1)-P(X=0,Y=-1)=
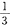
P(X=1,Y=-1)=P(Y=-1)-P(X=0,Y=-1)=
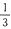
P(X=1,Y=1)=P(Y=1)-P(X=0,Y=1)=
故(X,Y)的概率分布为
(Ⅱ)

而
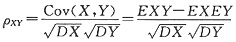
EXY=(-1)·1·
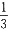
+1·1·
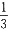
=0,故ρ
XY=0
9. 设二维随机变量(X,Y)服从区域G上的均匀分布,其中G是由x-y=0,x+y=2与y=0所围成的三角形区域。
(Ⅰ)求X的边缘密度f
X(x);
(Ⅱ)求P{X-Y≤1}。