一、信息技术基础 (每小题提供4个选项,只有一个选项符合题意)
三、填空题 1.
______.
[解析]
2. 两个质数的和是100,这两个质数的乘积最大是______.
2491
[解析] 若使两个质数的乘积最大.应使得这两个质数最接近.和为100的两个质数有3和97、11和89、17和83、29和71、41和59、47和53,其中47和53最接近,故两者乘积应为所求的最大乘积,是47×53=2491.
3. 在一个锅里烙饼.每次只能烙两张饼,两面都要烙,每面3分钟,烙9张饼需要______分钟.
27
[解析] 需要注意的是.不是每张饼都要将两面都烙好才出锅,两个面可以分开烙,而不是连续的,否则烙最后一张饼的两个面时,有半个锅是空着的,会浪费时间.所以烙饼要按面计算时间,已知每面3分钟.一锅同时烙两张饼,相当于3分钟烙两面,现在要烙9张饼共18面,故所需时间为18÷2×3=27(分钟).
4. 如果将五个分数
从大到小排成一列,中间的一个数是______.
[解析] 五个分数可化为
,按从大到小的顺序排列为
,则中间的数为
,即
.
5. a为自然数,当
为可约分数时,a的最小值是______.
11
[解析] 因为
为可约分数,可设x(3a+5)=y(a+8),整理得
,由于a为自然数,19又是质数,所以
可化为
(n∈N
+ )的形式,且n=1时,a有最小值11.
6. 一只蚯蚓白天向上爬3米,晚上滑下2米,照这样计算,蚯蚓从井底爬到井外(井高10米)需______天______夜.
8 7
[解析] 由已知可推得,当蚯蚓爬了7天7夜时,所在的位置距井底7米,所以只要第8天白天再向上爬3米即可爬到井外,不用再下滑2米了.
7. 一个最简分数,分子减去能被2、3整除的最小一位数,分母加上最小的质数,所得的分数的倒数是
,原来的最简分数是______.
[解析]
的倒数是
,最小的质数是2.能被2、3整除的最小的数是6,由此可得原来的最简分数为
.
8. 一块手表,每分钟比标准时间快2秒钟,早晨8时整将手表调准,问当这块手表第一次指向12时时,标准时间此时应是______.
11时52分
[解析] 由题干“每分钟比标准时间快2秒钟”可知,这块表走1小时比标准时间快2分钟.走4小时快8分钟,故手表第一次指向12时的标准时间为11时52分.
9. 有一串分数:
,…,其中第2013个数是______.
[解析] 原分数列可写成:
,其通式为
,所以第2013个数为
.
10. 甲、乙两港相距208千米,一艘船从甲港开往乙港,顺水行8小时到达,从乙港返回甲港,逆水行13小时到达,水流速度是______千米/时.
5
[解析] 设甲船速度是x千米/时,水流速度是y千米/时.由题意可得
解得
所以水流速度为5千米/时.也可直接列算术式求水流速度,(208÷8-208÷13)÷2=5(千米/时).
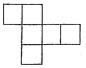
11. 一个正方形被分成5个相同的长方形(如下图),每个长方形的周长都是48厘米,这个正方形的周长是______厘米.
80
[解析] 设正方形边长为x厘米,则由题意可得
,解得x=20,所以正方形的周长为20×4=80厘米.也可以将5个长方形的周长加和。则由图可知,其和相当于12个正方形的边长的和,即是正方形周长的3倍,所以正方形周长为48×5÷3=80厘米.
12. 甲、乙、丙三人共有54元钱,甲用了自己钱数的
,乙用了自己钱数的
,丙用了自己钱数的
,各买了一支相同的钢笔,那么甲和丙两人剩下的钱共有______元.
14
[解析] 设甲有x元钱,乙有y元钱,丙有z元钱.由题意可得
解得
所以甲和丙两人剩下的钱共有
元.
13. 下图中直角梯形ABCD的面积是______cm
2 .
200
[解析] 由图可知,AB+CD=BC,所以
.
14. 甲、乙两人在跑道上以固定的速度练习赛跑,甲乙相距50米,两人同时出发,甲追乙,当甲追了100米时,还距乙10米,甲还要跑______米才能追上乙.
25
[解析] 设甲还要跑x米才能追上乙.由题意可知甲追了100米时,甲乙之间的距离缩短了40米,甲追上乙还要再跑x米.同时甲乙之间的距离缩短10米.由于甲乙速度不变,故
,解得x=25.即甲还要跑25米才能追上乙.
15. 有50张3元邮票和30张5元邮票,用这些邮票能组成______
292
[解析] 设3元的邮票用x张,5元的邮票用y张,则原题可转化为求满足
(x,y,k∈N
+ )的k的个数.当k取1,2,4,7,293,296,298,299这8个数时,方程组无解,所以k的个数为300-8=292,故用这些邮票能组成292种不同邮资.
四、判断题 1. 所有的偶数都是合数.
B
[解析] 0是偶数,但0既不是质数也不是合数;2是偶数,但2是质数而不是合数.故题干说法错误.
2. 真分数的倒数大于1,假分数的倒数一定比1小.
B
[解析] 真分数的倒数大于1,但假分数的倒数不一定比1小,也可能等于1.故题干说法错误.
3. 已知
,且A、B、C、D、E都不为0,把A、B、C、D、E按从小到大的顺序排列,第2个数是C.
B
[解析] 原式可化为100A=48B=80C=75D=50E,若A、B、C、D为正数,则按从小到大的顺序排列为A<C<D<E<B.第二个数是C,若A、B、C、D为负数,则从小到大的顺序排列为B<E<D<C<A.第二个数为E.因此题干说法错误.
4. 两人轮流报数,每次只能报1或2,把两人报的所有数加起来,谁报数后和是10,谁就获胜,如果你先报数,为了确保获胜,你第一次应报1.
A
[解析] 由题意得要想抢到报数后的和正好为10,那只要先抢到7就能获胜,因为此时无论对方报1还是2都无法达到10,又7=1+3+3,所以为了确保获胜,先报数时应报1.故题干说法正确.
5. 当水结成冰时,体积增加了
,当冰化成水时,体积减少了
.
B
[解析] 设水的体积为1,当水结成冰时,体积增加了
,变为
,冰再化成水时,体积重新变成1,此时体积减少了
.故题干说法错误.
6. 从一副扑克牌中拿出大小王,在剩下的52张中至少摸出17张,才能保证至少有5张牌是同花色的.
A
[解析] 当摸4次4张不同花色的牌,即摸16张以后,第17次再摸一张,至少有5张牌是同花色的.
7. 2005
5 的个位是5,2006
6 的个位是6,那么2007
7 的个位是7.
B
[解析] 20055 的个位是5,20066 个位是6,利用尾数法计算可得20077 的个位是3.故题干说法错误.
8. 一共有200kg糖,每袋装
kg,这些糖最多可以装满333袋,还剩2kg.
B
[解析] 由题意可得最多可以装的袋数为
袋,故最多可以装满333袋,还剩
袋,即
.题干说法错误.
五、选择题 (下列各题只有一个正确的答案)
6. 如图所示,用红、绿、蓝、黄四种颜色,涂编号为1、2、3、4的长方形,使任何相邻两个长方形的颜色都不同.一共有______种不同的涂法.
B
[解析] 四个长方形涂4种颜色有
种涂法,涂3种颜色有
种涂法,涂2种颜色有
种涂法,故共有24+48+12=84种涂法.
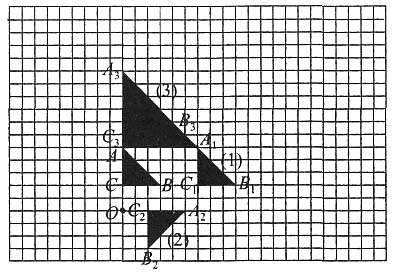
六、解答题 1. 按要求作图.
(1)画出把小旗向右平移6格后的图形.
(2)画出小旗绕O点按顺时针方向旋转90°后的图形.
(3)画出小旗按2:1扩大后的图形.
解:
2. 将厚度为0.1cm的纸在直径为10cm的圆筒上卷成直径为20cm的卷筒纸.你能求出这筒纸的总长度吗?(圆周率取3)
解:由题意可知,纸每绕网筒一圈,圆筒半径就增大0.1cm,故卷筒纸共有(20-10)÷2÷0.1=50层,而这50层纸的半径分别为5.1,5.2,5.3,…,9.9,10,
故这筒纸的总长度
.
答:这筒纸的总长度为2265cm.
3. 红领巾小学五、六年级的同学步行去森林公园春游,他们同时从学校出发,步行过程中速度不变.当五年级同学已行路程与未行路程的比是7:2时,六年级同学已行了5千米.当六年级同学到达森林公园时,五年级同学还有
的路程未行.红领巾小学到森林公园的路程有多少千米?
解:方法一:
设红领巾小学到森林公园的路程有x千米,五年级学生速度为a千米/时,六年级学生速度为b千米/时.
由题意可得:
解得x=6.
方法二:
根据已知,可列出计算红领巾小学到森林公园的路程的算式
.
答:红领巾小学到森林公园的路程有6千米.
4. 要运一批大米和面粉,若用小车运,每次能运2包大米和4包面粉,结果面粉运完了,大米还剩10包.若用大车运,每次能运6包大米和10包面粉,结果大米运完了,面粉还剩10包.求大米和面粉各有多少包?
解:设单独用小车运,到面粉运完,共运了x趟,单独用大车运,到大米运完,共运了y趟.
由题意可得
,解得
,
所以大米共有2×40+10=90包,面粉共有4×40=160包.
答:大米有90包,面粉有160包.
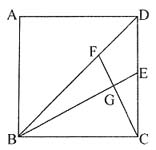
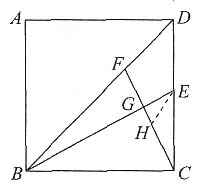
5. 如图,在正方形ABCD中,BF:FD=7:4,E是CD的中点,连接BE、CF交于点G,求CG:GF的比是多少?
解:如下图所示,过E作EF∥BD,交CF于H.
所以
,CH=FH,
又因为△EHG∽△BFG
所以
,
所以
,
所以
,
即CG:GF=11:7.
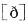 ,ABCD四个选项中“th”分别读[θ][θ][θ]
,ABCD四个选项中“th”分别读[θ][θ][θ]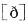 ,因此答案选D.
,因此答案选D.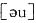 [au]
[au]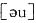
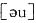 ,因此答案选B.
,因此答案选B.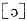 ,ABCD四个选项中“o”分别读
,ABCD四个选项中“o”分别读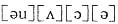 ,因此答案选C.
,因此答案选C.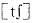 ,ABCD四个选项中“ch”分别读[k]
,ABCD四个选项中“ch”分别读[k]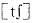 [k][k],因此答案选B.
[k][k],因此答案选B.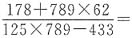 ______.
______.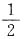
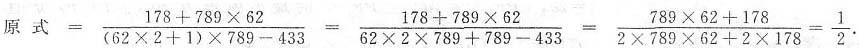
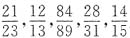 从大到小排成一列,中间的一个数是______.
从大到小排成一列,中间的一个数是______.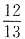
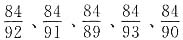 ,按从大到小的顺序排列为
,按从大到小的顺序排列为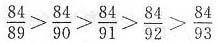 ,则中间的数为
,则中间的数为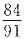 ,即
,即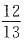 .
.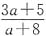 为可约分数时,a的最小值是______.
为可约分数时,a的最小值是______.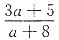 为可约分数,可设x(3a+5)=y(a+8),整理得
为可约分数,可设x(3a+5)=y(a+8),整理得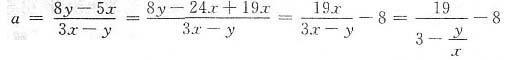 ,由于a为自然数,19又是质数,所以
,由于a为自然数,19又是质数,所以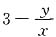 可化为
可化为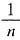 (n∈N+)的形式,且n=1时,a有最小值11.
(n∈N+)的形式,且n=1时,a有最小值11.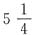 ,原来的最简分数是______.
,原来的最简分数是______.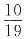
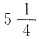 的倒数是
的倒数是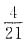 ,最小的质数是2.能被2、3整除的最小的数是6,由此可得原来的最简分数为
,最小的质数是2.能被2、3整除的最小的数是6,由此可得原来的最简分数为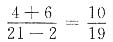 .
.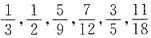 ,…,其中第2013个数是______.
,…,其中第2013个数是______.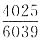
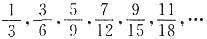 ,其通式为
,其通式为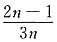 ,所以第2013个数为
,所以第2013个数为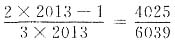 .
.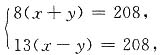 解得
解得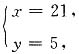 所以水流速度为5千米/时.也可直接列算术式求水流速度,(208÷8-208÷13)÷2=5(千米/时).
所以水流速度为5千米/时.也可直接列算术式求水流速度,(208÷8-208÷13)÷2=5(千米/时).
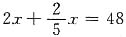 ,解得x=20,所以正方形的周长为20×4=80厘米.也可以将5个长方形的周长加和。则由图可知,其和相当于12个正方形的边长的和,即是正方形周长的3倍,所以正方形周长为48×5÷3=80厘米.
,解得x=20,所以正方形的周长为20×4=80厘米.也可以将5个长方形的周长加和。则由图可知,其和相当于12个正方形的边长的和,即是正方形周长的3倍,所以正方形周长为48×5÷3=80厘米.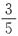 ,乙用了自己钱数的
,乙用了自己钱数的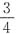 ,丙用了自己钱数的
,丙用了自己钱数的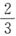 ,各买了一支相同的钢笔,那么甲和丙两人剩下的钱共有______元.
,各买了一支相同的钢笔,那么甲和丙两人剩下的钱共有______元. 解得
解得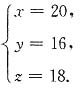 所以甲和丙两人剩下的钱共有
所以甲和丙两人剩下的钱共有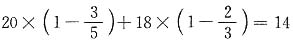 元.
元.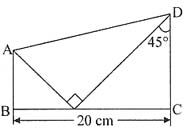
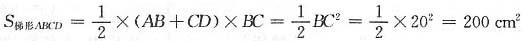 .
. ,解得x=25.即甲还要跑25米才能追上乙.
,解得x=25.即甲还要跑25米才能追上乙.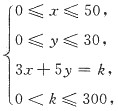 (x,y,k∈N+)的k的个数.当k取1,2,4,7,293,296,298,299这8个数时,方程组无解,所以k的个数为300-8=292,故用这些邮票能组成292种不同邮资.
(x,y,k∈N+)的k的个数.当k取1,2,4,7,293,296,298,299这8个数时,方程组无解,所以k的个数为300-8=292,故用这些邮票能组成292种不同邮资.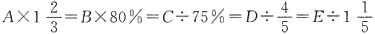 ,且A、B、C、D、E都不为0,把A、B、C、D、E按从小到大的顺序排列,第2个数是C.
,且A、B、C、D、E都不为0,把A、B、C、D、E按从小到大的顺序排列,第2个数是C.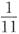 ,当冰化成水时,体积减少了
,当冰化成水时,体积减少了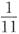 .
.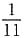 ,变为
,变为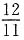 ,冰再化成水时,体积重新变成1,此时体积减少了
,冰再化成水时,体积重新变成1,此时体积减少了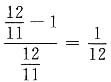 .故题干说法错误.
.故题干说法错误.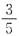 kg,这些糖最多可以装满333袋,还剩2kg.
kg,这些糖最多可以装满333袋,还剩2kg.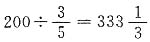 袋,故最多可以装满333袋,还剩
袋,故最多可以装满333袋,还剩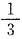 袋,即
袋,即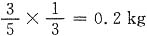 .题干说法错误.
.题干说法错误.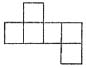
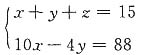 ,因5x-2y=44,又44和2y都是偶数,可知5x也是偶数,即x为偶数,且5x>44,即x>8.8,所以x≥10.当x=10时,y=3,z=2;当x=12时,y=8,z=-5<0,不合题意.故应取x=10,y=3,z=2,即有2道题未答.
,因5x-2y=44,又44和2y都是偶数,可知5x也是偶数,即x为偶数,且5x>44,即x>8.8,所以x≥10.当x=10时,y=3,z=2;当x=12时,y=8,z=-5<0,不合题意.故应取x=10,y=3,z=2,即有2道题未答. 种涂法,涂3种颜色有
种涂法,涂3种颜色有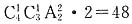 种涂法,涂2种颜色有
种涂法,涂2种颜色有 种涂法,故共有24+48+12=84种涂法.
种涂法,故共有24+48+12=84种涂法.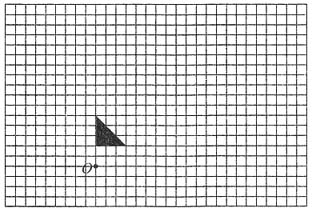
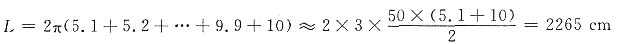 .
.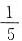 的路程未行.红领巾小学到森林公园的路程有多少千米?
的路程未行.红领巾小学到森林公园的路程有多少千米?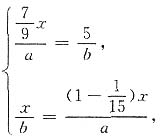
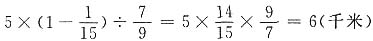 .
.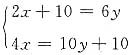 ,解得
,解得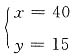 ,
,
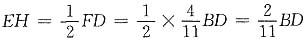 ,CH=FH,
,CH=FH,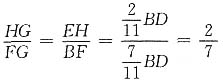 ,
,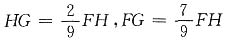 ,
, ,
,