一、选择题 (在每小题列出的四个备选项中只有一个是符合题目要求的)
1. 下列运算正确的是______.
A.
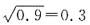
B.0.1
3=0.0001
C.
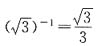
D.
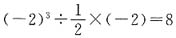
A B C D
C
[解析] A项,
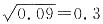
,故A项错误;B项,0.1
3=0.001,故B项错误;D项,
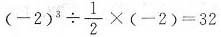
,故D项错误.C项运算正确.故答案选C.
6. 在“x
2□2xy□y
2”的空格□中,分别填上“+”或“-”,在所得的代数式中,能构成完全平方式的概率是______.
A.

B.
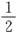
C.
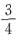
D.1
A B C D
B
[解析] 在方框中填“+”或“-”共有4种填法,分别为“+-”“++”“-+”“--”.当填入“++”“-+”时,能构成完全平方式,故概率为
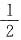
.
7. 若a∈R,则“a=1”是“复数z=a
2-1+(a+1)i是纯虚数”的______.
- A.充分非必要条件
- B.必要非充分条件
- C.充要条件
- D.既不充分也不必要条件
A B C D
C
[解析] 当a=1时,复数z=2i,为纯虚数,故a=1是复数z=a
2-1+(a+1)i是纯虚数的充分条件;当复数z=a
2-1+(a+1)i是纯虚数时,即
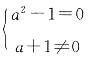
,求得a=1,故a=1是复数z=a
2-1+(a+1)i是纯虚数的必要条件.因此答案为C.
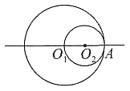
8. 如图,⊙O
1和⊙O
2内切于点A,其半径分别是4和2,将⊙O
2沿直线O
1O
2平移至两圆外切时,⊙O
2移动的距离是______.
A B C D
D
[解析] 当⊙O2向右平移时,若使⊙O2与⊙O1外切,则移动距离为4;当⊙O2向左平移时,若使⊙O2与⊙O1外切,则移动距离为8时,故答案为D.
11. 已知点(-5,y
1),(1,y
2),(10,y
3)在函数y=(x-2)
2+c的图象上,则y
1,y
2,y
3的大小关系是______.
- A.y1>y2>y3
- B.y3>y1>y2
- C.y3>y2>y1
- D.y2>y1>y3
A B C D
B
[解析] 将三个点分别带入函数可得,y1=49+c,y2=1+c,y3=64+c.故y3>y1>y2.本题也可根据二次函数图象的对称性进行判断.
12. 在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,若a=2,b=3,
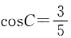
,则△ABC的面积等于______.
A.
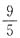
B.
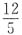
C.
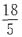
D.
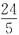
A B C D
B
[解析] 根据三角形的面积公式可得
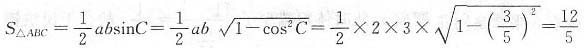
.
14. 如图,在某公园高为60米的观测塔CD的顶端C处测得两景点A,B的俯角分别是30°和60°,且点A、D、B在同一条直线上,则景点A、B之间的距离为______米.
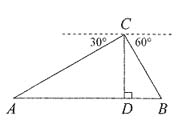
A.
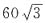
B.

C.
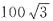
D.
A B C D
B
[解析] 由图可知,∠ACB=90°,∠A=30°,∠B=60°,所以
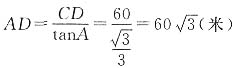
,
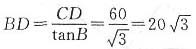
(米),故
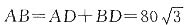
(米).
15. 要得到
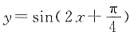
的图象,只需将y=sin2x的图象______.
A.向左平移
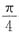
个单位
B.向右平移
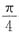
个单位
C.向左平移
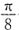
个单位
D.向右平移
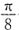
个单位
A B C D
C
[解析] 因为
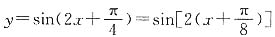
,所以只需将y=sin2x的图象向左平移
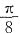
个单位即可得到
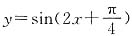
的图象,故答案选C.
二、综合知识判断题3. “丝绸之路”是古代横跨亚、美两洲,各国进行陆路贸易的商旅大道.
对 错
B
[解析] 丝绸之路是指起始于古代中国,连接亚洲、非洲和欧洲的古代路上商业贸易路线.故题干说法错误.
5. 《国家中长期教育改革和发展规划纲要(2010—2020年)》指出,我国教育的战略目标是:到2020年,基本普及义务教育,基本形成学习型社会,进入人力资源强国行列.
对 错
B
[解析] 《国家中长期教育改革和发展规划纲要(2010—2020年)》指出,我国教育的战略目标是:到2020年,基本实现教育现代化,基本形成学习型社会,进入人力资源强国行列.故题干说法错误.
三、填空题1. 若关于x的方程
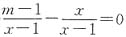
有增根,则m的值是______.
2
[解析] 在分式方程化为整式方程的过程中,若整式方程的根能使此方程的最简公分母为零,那么这个根就是原分式方程的增根,所以方程
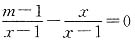
的增根应为x=1.原方程化为整式方程得m=x+1,又原方程有增根x=1,所以m=2.
2. 若
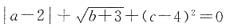
,则c-b
a=______.
-5
[解析] 由题意可得

所以c-b
a=4-(-3)
2=-5.
3. 若函数
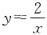
与y=x-1的图象的交点坐标为(a,b),则
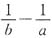
的值为______.
[解析] 因为函数
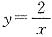
与y=x-1的图象交于(a,b),即
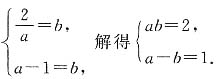
所以
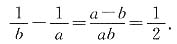
4. 若α是第四象限的角,
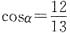
,则sinα=______.
[解析] 因为
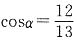
,所以
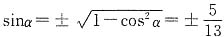
.又因为α是第四象限的角,即sinα<0,所以
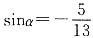
.
5. 如下图,将矩形纸片ABCD沿EF折叠,使点D与BC边的中点D'重合,若BC=8,CD=6,则CF=______.
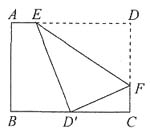
[解析] 由题于可知DF=D'F,设CF=x,则DF=6-x,即D'F=DF=6-x.又BC=8,D'为BC的中点,所以D'C=4.在Rt△D'CF中,D'F
2=D'C
2+CF
2,即(6-x)
2=4
2+x
2,解得
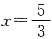
,所以
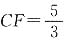
.
6. 如下图,函数y=ax-1的图象过点(1,2),则不等式ax-1>2的解集是______.
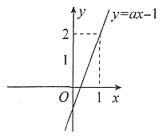
{x|x>1}>1
[解析] 因为函数y=ax-1过点(1,2),所以将其代入即a-1=2,解得a=3.所以不等式ax-1>2可化为3x-1>2,解得x>1,所以解集为{x|x>1}.
7. 已知椭圆
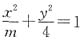
的离心率
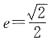
,则m的值等于______.
2或8
[解析] 当m>4时,椭圆离心率
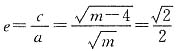
,解得m=8;当m<4时,椭圆离心率
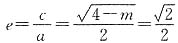
,解得m=2,所以m=2或m=8.
8. 如下图,AB是⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且CO=CD,则∠PCA的度数是______.

67.5°
[解析] 因为PD与圆O相切,所以∠OCD=∠OCP=90°.又CO=CD,则∠COD=∠D=45°.因为OC=OA,∠COD=∠DAC+∠OCA,所以

,所以∠PCA=∠OCP-∠OCA=67.5°.
9. 圆x
2+y
2-2y-4=0的圆心到直线3x+4y-6=0的距离为______.
[解析] 圆x
2+y
2-2y-4=0可化为x
2+(y-1)
2=5,故其圆心坐标为(0,1).圆心O(0,1)到直线3x+4y-6=0的距离
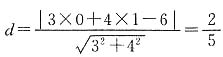
.
10. 设平面向量a=(3,5),b=(-2,1),则a-2b=______.
(7,3)
[解析] a-2b=(3,5)-(-2×2,1×2)=(3+4,5-2)=(7,3).
四、解答题1. 先化简
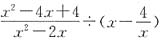
,然后从
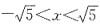
的范围内选取一个合适的整数作为x的值代入求值.
解:
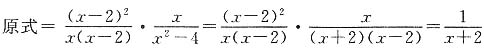
,
又因为
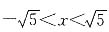
,且x≠0,x≠±2,
所以取x=1,则原式=

.(取x=-1亦可)
2. 填空:在由原方程得到方程①的过程中,利用了______法,体现了______的数学思想;
3. 在实数范围内求出原方程的解.
解:设x2-x=y,则原方程可化为y2-4y-12=0,
解得y1=6,y2=-2.
当y=6时,x2-x=6,解得x1=-2,x2=3;
当y=-2时,x2-x=-2,Δ<0,此方程无实数根.
所以原方程的解为x1=-2,x2=3.
4. 求中三等奖的概率;
解:设“中三等奖”的事件为A,“中奖”的事件为B,“中一等奖”的事件为C,“中二等奖”的事件为D.
因为“中三等奖”的情况有4种,故其概率
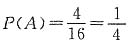
.
5. 求中奖的概率.
解:“中一等奖”的情况有2种,其概率
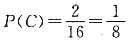
,
“中二等奖”的情况有3种,其概率
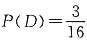
,
则由互斥事件的加法公式得,
“中奖”的概率
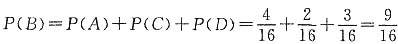
.
6. 已知{a
n}是公差不为零的等差数列,a
1=7,且a
3,a
6,a
10成等比数列.求数列{a
n}前20项的和S
20.
解:设数列{a
n}的公差为d,则由a
1=7,且a
3,a
6,a
10成等比数列得,
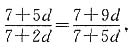
解得d=1或d=0,
由题意可知,公差d≠0,所以d=1.
所以
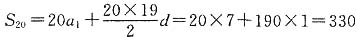
.
7. 如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.请判断CD与⊙O的位置关系,并说明理由.
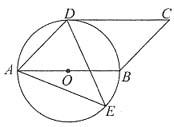
解:CD与⊙O相切.
理由:连接OD,如下图所示.
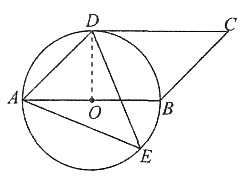
因为∠AED=45°,所以∠AOD=90°,
因为四边形ABCD是平行四边形,所以DC∥AB.
所以∠CDO=∠AOD=90°,即OD⊥CD,
又因为OD是⊙O的半径,
所以CD是⊙O的切线.
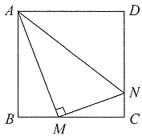
8. 求证:△ABM∽△MCN;
证明:因为四边形ABCD是正方形,所以∠B=∠C=90°,∠BAM+∠AMB=90°.
因为AM⊥MN,所以∠AMN=90°,∠AMB+∠CMN=90°.
所以∠BAM=∠CMN,∠AMB=∠MNC,所以△ABM∽△MCN.
9. 设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式;当点M运动到什么位置时,梯形ABCN的面积最大?并求出最大值.
解:由上一小题的证明可知,△ABM∽△MCN,
所以
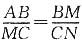
,即
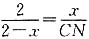
,
所以
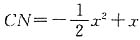
,
所以
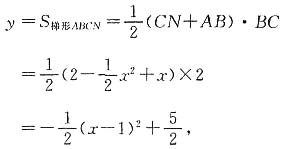
所以当x=1时,y有最大值,最大值为
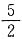
,此时M运动到BC的中点.
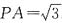 .
.
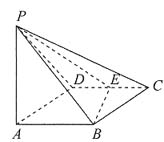
10. 证明:平面PBE⊥平面PAB;
证明:如图所示,连接BD.

因为四边形ABCD是菱形,且∠BCD=60°,所以△BCD为等边三角形.
又因为E是CD的中点,所以BE⊥CD,
又因为AB∥CD,所以BE⊥AB.
又PA⊥平面ABCD,BE
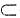
平面ABCD,所以PA⊥BE.
而PA∩AB=A,所以BE⊥平面PAB,
又BE
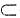
平面PBE,所以平面PBE⊥平面PAB.
11. 求二面角A-BE-P的大小.
由上一小题知,BE⊥平面PAB,PB
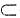
平面PAB,所以PB⊥BE,
又AB⊥BE,所以∠PBA是二面角A-BE-P的平面角.
在Rt△PSB中,
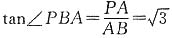
,
因为∠PBA∈(0,π)所以∠PBA=60°,
所以二面角A-BE-P的大小是60°.
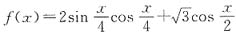 .
.13. 令
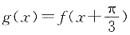
,判断函数g(x)的奇偶性,并说明理由.
证明:由上一小题可知,
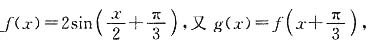
所以
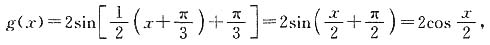
又
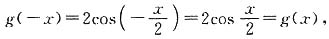
所以函数g(x)是偶函数.
14. 求椭圆C的方程;
解:由题意设椭圆C的方程为
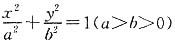
,且可知左焦点为F'(-2,0).
又|AF|=3,
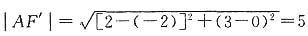
,
从而有
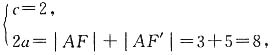
解得
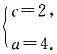
又c
2=a
2-b
2,所以b
2=12,
所以椭圆C的方程为
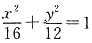
.
15. 是否存在平行于OA的直线l,使得直线l与椭圆C有公共点,且直线OA与l的距离等于4?若存在,求出直线l的方程;若不存在,说明理由.
解:假设存在符合题意的直线l,其方程为
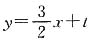
,
则由
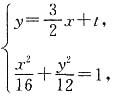
得3x
2+3tx+t
2-12=0.
因为直线l与椭圆C有公共点,
所以Δ=(3t)
2-4×3(t
2-12)≥0,解得
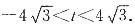
又因为直线OA与l的距离d=4,所以
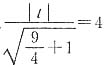
.
解得
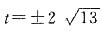
.
由于
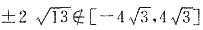
,所以符合题意的直线l不存在.
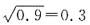
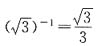
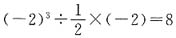
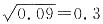 ,故A项错误;B项,0.13=0.001,故B项错误;D项,
,故A项错误;B项,0.13=0.001,故B项错误;D项,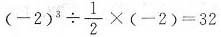 ,故D项错误.C项运算正确.故答案选C.
,故D项错误.C项运算正确.故答案选C.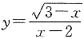 中,自变量x的取值范围是______.
中,自变量x的取值范围是______.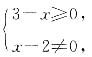 解得x≤3且x≠2.
解得x≤3且x≠2.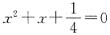 根的情况是______.
根的情况是______. ,故方程有两个相等的实数根.
,故方程有两个相等的实数根.
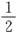
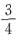
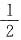 .
.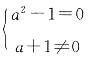 ,求得a=1,故a=1是复数z=a2-1+(a+1)i是纯虚数的必要条件.因此答案为C.
,求得a=1,故a=1是复数z=a2-1+(a+1)i是纯虚数的必要条件.因此答案为C.
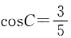 ,则△ABC的面积等于______.
,则△ABC的面积等于______.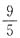
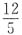
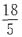
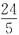
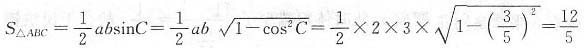 .
. ABCD的周长为22cm,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于点E,则△ABE的周长为______.
ABCD的周长为22cm,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于点E,则△ABE的周长为______.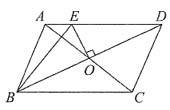
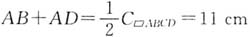 ,C△ABE=AB+BE+AE=AB+DE+AE=AB+AD=11cm.
,C△ABE=AB+BE+AE=AB+DE+AE=AB+AD=11cm.
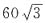

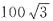
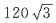
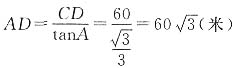 ,
,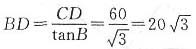 (米),故
(米),故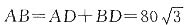 (米).
(米).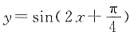 的图象,只需将y=sin2x的图象______.
的图象,只需将y=sin2x的图象______.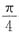 个单位
个单位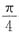 个单位
个单位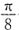 个单位
个单位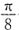 个单位
个单位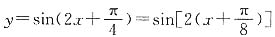 ,所以只需将y=sin2x的图象向左平移
,所以只需将y=sin2x的图象向左平移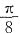 个单位即可得到
个单位即可得到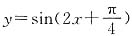 的图象,故答案选C.
的图象,故答案选C.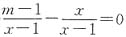 有增根,则m的值是______.
有增根,则m的值是______.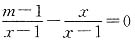 的增根应为x=1.原方程化为整式方程得m=x+1,又原方程有增根x=1,所以m=2.
的增根应为x=1.原方程化为整式方程得m=x+1,又原方程有增根x=1,所以m=2.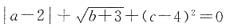 ,则c-ba=______.
,则c-ba=______. 所以c-ba=4-(-3)2=-5.
所以c-ba=4-(-3)2=-5.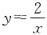 与y=x-1的图象的交点坐标为(a,b),则
与y=x-1的图象的交点坐标为(a,b),则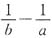 的值为______.
的值为______.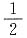
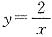 与y=x-1的图象交于(a,b),即
与y=x-1的图象交于(a,b),即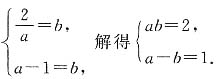 所以
所以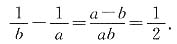
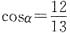 ,则sinα=______.
,则sinα=______.
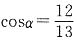 ,所以
,所以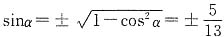 .又因为α是第四象限的角,即sinα<0,所以
.又因为α是第四象限的角,即sinα<0,所以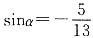 .
.
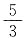
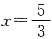 ,所以
,所以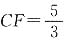 .
.
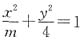 的离心率
的离心率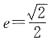 ,则m的值等于______.
,则m的值等于______.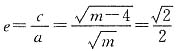 ,解得m=8;当m<4时,椭圆离心率
,解得m=8;当m<4时,椭圆离心率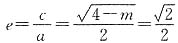 ,解得m=2,所以m=2或m=8.
,解得m=2,所以m=2或m=8.
 ,所以∠PCA=∠OCP-∠OCA=67.5°.
,所以∠PCA=∠OCP-∠OCA=67.5°.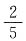
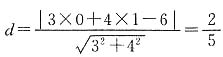 .
.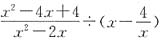 ,然后从
,然后从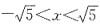 的范围内选取一个合适的整数作为x的值代入求值.
的范围内选取一个合适的整数作为x的值代入求值.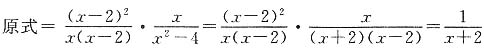 ,
,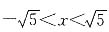 ,且x≠0,x≠±2,
,且x≠0,x≠±2, .(取x=-1亦可)
.(取x=-1亦可)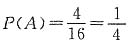 .
.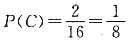 ,
,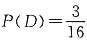 ,
,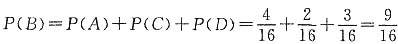 .
.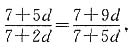
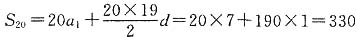 .
.


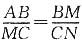 ,即
,即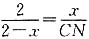 ,
,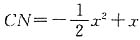 ,
,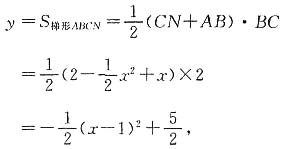
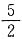 ,此时M运动到BC的中点.
,此时M运动到BC的中点.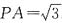 .
.

 平面ABCD,所以PA⊥BE.
平面ABCD,所以PA⊥BE. 平面PBE,所以平面PBE⊥平面PAB.
平面PBE,所以平面PBE⊥平面PAB. 平面PAB,所以PB⊥BE,
平面PAB,所以PB⊥BE,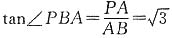 ,
,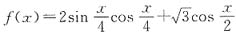 .
.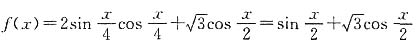
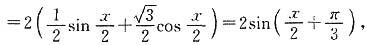
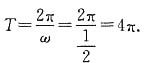
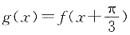 ,判断函数g(x)的奇偶性,并说明理由.
,判断函数g(x)的奇偶性,并说明理由.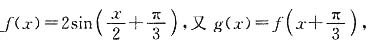
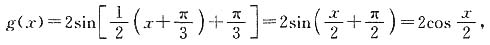
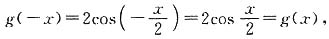
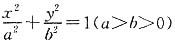 ,且可知左焦点为F'(-2,0).
,且可知左焦点为F'(-2,0).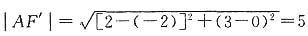 ,
,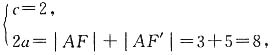
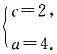
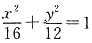 .
.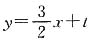 ,
,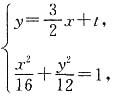 得3x2+3tx+t2-12=0.
得3x2+3tx+t2-12=0.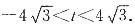
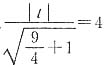 .
.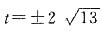 .
.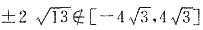 ,所以符合题意的直线l不存在.
,所以符合题意的直线l不存在.