单项选择题1. 某建筑基槽宽5m,长20m,开挖深度为6m,基底以下为粉质黏土。在基槽底面中间进行平板载荷试验,采用直径为800mm的圆形承压板。载荷试验结果显示,在p-s曲线线性段对应100kPa压力的沉降量为6mm。试计算,基底土层的变形模量E
o值最接近下列哪个选项?
- A.6.3MPa
- B.9.0MPa
- C.12.3MPa
- D.14.1MPa
A B C D
B
[解析] 首先判断该试验属于浅层还是深层平板载荷试验:虽然试验深度为6m,但基槽宽度已大于承压板直径的3倍,故属于浅层载荷试验。
根据《岩土工程勘察规范》GB 50021—2001(2009年版)公式(10.2.5-1)计算变形模量:
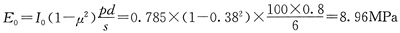
该题的考点在于确定平板载荷试验的试验条件,究竟属于浅层还是深层。深层载荷试验和浅层载荷试验的区别在于,试土是否存在边载,荷载是否作用于半无限体的内部。同时,即使有边载存在,如果试验深度过浅(边载过小)也不符合深层载荷试验变形模量计算假定荷载作用于半无限体内部的条件。因此,《岩土工程勘察规范》GB 50021—2001(2009年版)规定:“深层平板载荷试验的试验深度不应小于5m”;“浅层平板载荷试验的试坑宽度或直径不应小于承压板宽度或直径的三倍;深层平板载荷试验的试井直径应等于承压板直径;当试井直径大于承压板直径时,紧靠承压板周围土的高度不应小于承压板直径”。据此,题目给定的条件应属浅层平板载荷试验。
公式(10.2.5-1)中,I
o为承压板的形状系数(圆形板为0.785,方形板为0.866),μ为土的泊松比,规范都已给出,注意不要用错。
若不加判断或判断错误,按规范深层载荷板公式(10.2.5-2)计算:
E
o=
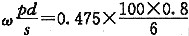
=6.33MPa
会选择错误答案A。
阅卷中发现有考生看到试验深度为6m,就简单地判定为深层载荷试验,而导致解答错误的情况。
2. 取网状构造冻土试样500g,待冻土样完全融化后,加水调成均匀的糊状,糊状土质量为560g,经试验测得糊状土的含水量为60%。问冻土试样的含水量最接近下列哪个选项?
A B C D
A
[解析] 直接由《土工试验方法标准》公式(4.0.6)计算
ω=
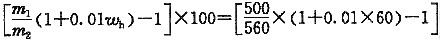
×100=42.9%
该题可不用规范公式,直接通过指标换算得出答案。
该题是希望考生了解冻土的特殊构造以及冻土试验的一些特殊要求。对于层状和网状结构的冻土,由于结冰水在土中赋存的不均匀,测含水量时要求取较大的试样,待其完全融化后,调成均匀糊状(土太湿时,多余的水分让其自然蒸发或用吸球吸出,但不得将土粒带出;土太干时,可适当加水),测求糊状土的含水量,再换算出原状冻土的含水量。
最简单的解题方法是由规范给定的公式直接计算得出答案,考生也可通过土的三相指标换算得出答案:
设试样中土粒质量为m
s(注意:试验过程中土粒质量没有变化)
m
s×60%+m
s=560
m
s=350g
原状冻土的含水量为:(500-350)/350=42.9%
结果一样。
3. 取某土试样2000g,进行颗粒分析试验,测得各级筛上质量见下表,筛底质量为560g。已知土样中的粗颗粒以棱角形为主,细颗粒为黏土。问下列哪一选项对该土样的定名最准确?
颗粒分析试验结果
| 孔径(mm) | 20 | 10 | 5 | 2.0 | 1.0 | 0.5 | 0.25 | 0.075 |
| 筛上质量(g) | 0 | 100 | 600 | 400 | 100 | 50 | 40 | 150 |
A B C D
C
[解析] 首先看颗分结果:大于2mm颗粒含量=(100+600+400)/2000=55%,大于50%
粗颗粒以棱形为主,属角砾;
再看小于0.075mm的细颗粒含量为
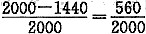
=28%,大于25%,属混合土;
细颗粒为黏土,定名为含黏土角砾。
上年度试题中曾有一道关于混合土的知识题,考生答对率很低。混合土作为一种特殊土,由于其工程性质的特殊性,在勘察、测试和评价方面有着不同的要求,希望引起重视。
目前土的分类和定名主要依据颗粒级配或塑性指数。
《岩土工程勘察规范》GB 50021—2001(2009年版)第6.4.1条规定:
由细粒土和粗粒土混杂且缺乏中间粒径的土应定名为混合土。
当碎石土中粒径小于0.075mm的细粒土质量超过总质量的25%时,应定名为粗粒混合土;当粉土或黏性土中粒径大于2mm的粗粒土质量超过总质量的25%时,应定名为细粒混合土。
对混合土的细分定名,规范第3.3.6条第3款规定:“对混合土,应冠以主要含有的土类定名”,并在条文说明中给出了定名的示例。
该题在解题时须注意,土样的总质量为2000g,筛底质量即为小于0.075mm的细颗粒质量为560g。
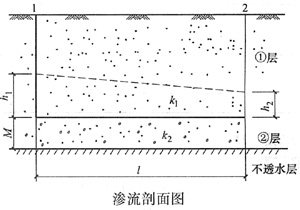
4. 图为一工程地质剖面图,图中虚线为潜水水位线。已知:h
1=15m,h
2=10m,M=5m,l=50m,第①层土的渗透系数k
1=5m/d,第②层土的渗透系数k
2=50m/d,其下为不透水层。问通过1、2断面之间的单宽(每米)平均水平渗流流量最接近下列哪个选项的数值?
- A.6.25m3/d
- B.15.25m3/d
- C.25.00m3/d
- D.31.25m3/d
A B C D
D
[解析] 1、2两断面间的水力梯度:i=
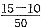
=0.1
第1层土的单宽渗流流量:q
1=
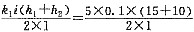
=6.25m
3/d
第2层土的单宽渗流流量:q
2=k
2iM×1=50×0.1×5×1=25m
3/d
整个断面的渗流流量:q=q
1+q
2=6.25+25=31.25m
3/d
答案D。
若只计算第一层的渗流量,为答案A。
题图所给出的为一典型的冲积层二元结构,通常下部为河床相沉积,颗粒较粗;上部
为河漫滩相沉积,颗粒较细。地下水为潜水,稳定层流运动,符合达西定律:q=kiA。
依照达西定律,分层按平均断面计算即可得出正确答案。
本题亦可按照等效渗透系数计算:
取中间断面,按流量相等的条件计算的水平向等效渗透系数为:
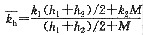
=17.86m/d
q=
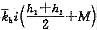
×1=17.86×0.1×17.5=31.25m
3/d
5. 在地面作用矩形均布荷载p=400kPa,承载面积为4m×4m。试求承载面积中心O点下4m深处的附加应力与角点C下8m深处的附加应力比值,最接近下列何值?(矩形均布荷载中心点下竖向附加应力系数α
o可由下表查得)
附加应力系数αo | z/b | l/b |
|
| 1.0 | 2.0 |
| 0.0 | 1.000 | 1.000 |
| 0.5 | 0.701 | 0.800 |
| 1.0 | 0.336 | 0.481 |
A B C D
D
[解析] (1)求σ
zo:由z/b=4/4=1.0,l/b=4/4=1.0,查表得α
o=0.336
承载面积中心O点下z=4m处M
o点的附加应力σ
zo=α
op=0.336×400=134.4kPa
(2)求σ
zc:由

=1.0,
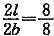
=1.0,查表得α
o=0.336
承载面积角点C下z=8m处M
c点的附加应力σ
zc=

×0.336×400=33.6kPa
(3)
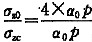
=4
本题考点是:求解矩形面积上均布荷载作用下基础底面下各点附加应力。
基础下各点的附加应力采用布辛奈斯克解公式求解,设矩形面积的长度和宽度分别为l和b,作用于地基上的竖向均布荷载为p
o,利用角点应力表达式和叠加原理,可以计算平面上任一点下任意深度z处的附加应力值。根据《建筑地基基础设计规范》附录K,由z/b、z/b可以查出角点下的附加应力系数,则附加应力σ
z=α·p
o。
求中心点下的附加应力系数时,通过中心点将方形承载面积划分为4个小的方形面积,利用角点应力表达式和叠加原理,求长度和宽度分别为
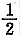
l和
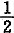
面积下的角点的
附加应力系数,再乘以4。
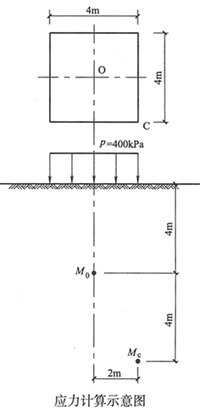
本题给出的是中心点附加应力系数表,从表中可查出中心点下的附加应力系数,计算角点下的附加应力系数时,求长度和宽度分别为2l和2b面积下的中心点的附加应力系数,再除以4,则附加应力σ
z=α·p
o。
根据《建筑地基基础设计规范》附录K,计算过程如下:
(1)求σ
zo:由
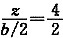
=2,
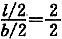
=1,查表得
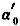
=0.084
则α
o=4×0.084=0.336
承载面积中心O点下z=4m处M
o点的附加应力σ
zo=α
op=0.336×400=134.4kPa
(2)求σ
zc:由z/b=8/4=2,l/b=4/4=1.0查表得α
o=0.084
承载面积角点C下z=8m处M
c点的附加应力σ
zc=α
op=0.084×400=33.6kPa
(3)
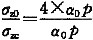
=4
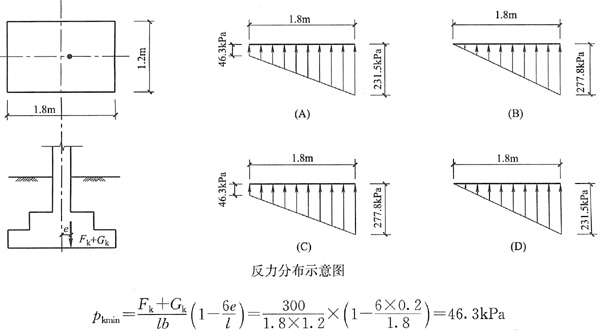
6. 如图所示柱基础底面尺寸为1.8m×1.2m,作用在基础底面的偏心荷载F
k+G
k=300kN,偏心距e=0.2m,基础底面应力分布最接近下列哪个选项?
A B C D
A
[解析] e=0.2m<b/6=1.8/6=0.3m 为小偏心
p
kmax=
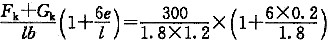
=231.48KPa
解答时,先做小偏心判断,确定应力分布为梯形,然后只计算P
max亦可。
本题考点是:掌握偏心荷载作用下,基础底面压力分布的计算方法。
偏心荷载作用下,基础底面压力分布分为梯形和三角形两种。首先应计算偏心距e,并与b/6比较,当e<b/6时为小偏心,荷载分布为梯形,当e>b/6时,为大偏心,荷载分布为三角形。
小偏心、荷载为梯形时,根据《建筑地基基础设计规范》中公式(5.2.2-2)及公式(5.2.2-3),计算基础边缘应力的最大值及最小值。
p
kmax=
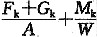
p
kmin=
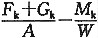
其中M
k=(F
k+G
k)e W=
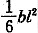
代入以上两式,得
p
kmax=
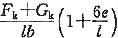
p
kmin=
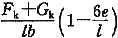
当偏心距e>b/6时,为大偏心,荷载分布为三角形,p
kmax应按下式计算:
p
kmax=
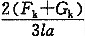
7. 如图所示矩形基础,地基土的天然重度γ=18kN/m
3,饱和重度γ
sat=20kN/m
3,基础及基础上土重度γ
G=20kN/m
3,η
b=0,η
d=1.0。估算该基础底面积最接近下列何值?
- A.3.2m2
- B.3.6m3
- C.4.2m2
- D.4.6m2
A B C D
B
[解析] (1)求地基承载力特征值
f
a=f
ak+η
bγ(b-3)+η
dγ
m(d-0.5)=150+1.0×18×(1.5-0.5)=168kPa
(2)确定基础底面积
按中心荷载作用计算基底面积
p
k=
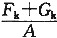
计算 p
k=f
a时的基底面积
则 f
a=
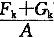
其中 G
k=γ
GdA
A=
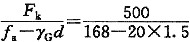
=3.62m
2 答案B。
本题考点是:轴心荷载作用时基础底面处平均压力计算及地基承载力深度与宽度修正。
图中给出了持力层地基承载力特征值f
ak=150kPa,当基础宽度大于3m或埋置深度大于0.5m时,地基承载力特征值,尚应按下式修正:
f
a=f
ak+η
bγ(b-3)+η
dγ
m(d-0.5) 式中 f
a——修正后的地基承载力特征值;
f
ak——地基承载力特征值;
η
b、η
d——基础宽度和埋深的地基承载力修正系数;
γ——基础底面以下土的重度,地下水位以下取浮重度;
b——基础底面宽度(m),当基宽小于3m按3m取值,大于6m按6m取值;
γ
m——基础底面以上土的加权平均重度,地下水位以下取浮重度;
d——基础埋置深度(m)。
根据《建筑地基基础设计规范》,当轴心荷载作用时
p
k≤f
a 则计算 P
k=f
a时的基底面积
p
k=
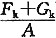
=f
a 其中 G
k=γ
GdA,F
k=500kN
解简单的一元一次方程,可得:
A=
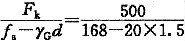
=3.62m
2 需注意的是,计算中γ
m应使用基础以上土的天然重度18kN/m
3,如使用饱和重度γ
sat=20kN/m
3,则为错误结果。
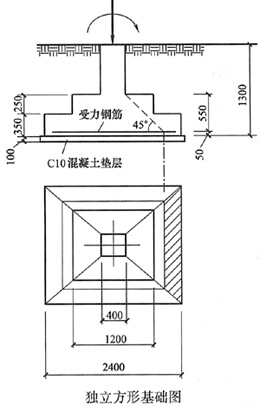
8. 如图所示(图中单位为mm),某建筑采用柱下独立方形基础,拟采用C20钢筋混凝土材料,基础分二阶,底面尺寸2.4m×2.4m,柱截面尺寸为0.4m×0.4m。基础顶面作用竖向力700kN,力矩87.5kN·m,问柱边的冲切力最接近下列哪个选项?
- A.95kN
- B.110kN
- C.140kN
- D.160kN
A B C D
C
计算偏心距e=M/F=87.5/700=0.125m<2.4/6=0.4m属小偏心
2.计算基底最大净反力p
jmax=
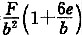
=700/2.4
2×(1+6×0.125/2.4)
=159.5kPa
3.基础有效高度h
o=0.55m,阴影宽度=2.4/2-0.4/2-0.55=0.45m
4.冲切力=p
jmax×A
l=159.5×
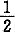
×0.45×(2.4+2.4-2×0.45)=139.96kN
本题考点是:计算偏心荷载作用下,方形扩展基础所承受的冲切力。
根据《建筑地基基础设计规范》,应按下列公式计算:
F
l=P
jA
l式中 p
j,——扣除基础自重及其上土重后相应于荷载效应基本组合时的地基土单位面积净反力,对偏心受压基础可取基础边缘处最大地基土单位面积净反力;
A
l——冲切验算时取用的部分基底面积;
F
l——相应于荷载效应基本组合时作用在A
l上的地基土净反力设计值。
因此,本题需计算两个参数,一是基础边缘处最大地基土单位面积净反力,一是冲切验算时取用的部分基底面积,也就是图中阴影部分的面积。
在计算基础边缘处最大地基土单位面积净反力之前,首先应进行偏心状态判断,计算偏心距e=M/F=87.5/700=0.125m<2.4/6=0.4m属小偏心。反力分布为梯形,计算公式如下:
p
kmax=
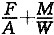
其中 M=F·e,l=b,W=
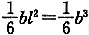
代入上式,得 p
jmax=
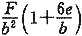
冲切破坏锥体的底面落在基础底面以内,计算柱与基础交接处的冲切力,A
l即为阴影部分面积。这是个梯形,由图中可以得出,基础有效高度h
o=0.55m,则阴影宽度=2.4/2-0.4/2-0.55=0.45m,梯形下底为2.4m,上底为2.4-2×0.45=1.5m,则梯形面积为A
l=
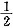
×0.45×(2.4+2.4-2×0.45)
梯形上底计算也可取柱宽加两倍基础有效高度:0.4+2×0.55=1.5m
10. 桩基承台如图所示(尺寸以mm计),已知柱轴力F=12000kN,力矩M=1500kN·m,水平力H=600kN(F、M和H均对应荷载效应基本组合),承台及其上填土的平均重度为20kN/m
3。试按《建筑桩基技术规范》JGJ 94—2008计算图示虚线截面处的弯矩设计值最接近下列哪一数值?
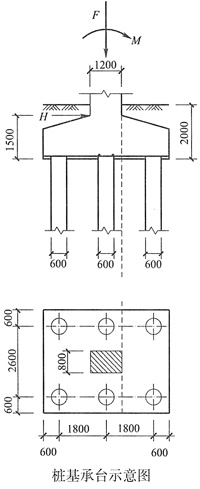
- A. 4800kN·m
- B. 5300kN·m
- C. 5600kN·m
- D. 5900kN·m
A B C D
C
[解析] 首先应清楚该题属于桩基础承台结构的抗弯承载力验算。根据《建筑桩基技术规范》JGJ 94—2008第5.9.1条与第5.9.2条及公式(5.9.2-2)计算如下:
先计算右侧两基桩净反力设计值:
(1)右侧两根基桩的净反力:
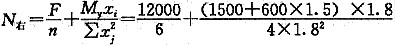
=2333KN
(2)弯矩设计值:M
Y=∑N
iχ
i=2×2333×(1.8-0.6)=5599kN·m
该题考察内容为桩基结构承载力计算,故题中给的荷载条件为传至承台顶面的荷载效应基本组合。考点为桩基承台抗弯承载力验算时,要取基桩的净反力计算。根据试验研究及理论分析,柱下独立桩基承台抗弯承载力验算,一般取在柱边和承台变阶处的正截面弯矩设计值进行计算。因由承台及其上填土的自重及其引起的基桩和基底反力对验算截面产生的弯矩大小相等,方向相反,故可不必计算,题中给出的承台及其上填土的平均重度参数属于“干扰”条件。
该题的关键为正确计算由外部荷载引起的基桩净反力,进而计算由其产生的对计算截面的弯矩。由于题中无特殊说明,故应理解为一般建筑物和受水平力(包括力矩与水平剪力)较小的高层建筑群桩基础,且没给出桩长等条件,不必考虑承台底地基土分担荷载的作用,可直接按《建筑桩基技术规范》JGJ 94—2008第5.1.1条和公式(5.1.1-1)计算群桩中基桩的桩顶作用效应。
12. 某抗拔基桩桩顶拔力为800kN,地基土为单一的黏土,桩侧土的抗压极限侧阻力标准值为50kPa,抗拔系数λ取为0.8,桩身直径为0.5m,桩顶位于地下水位以下,桩身混凝土重度为25kN/m
3,按《建筑桩基技术规范》JGJ 94—2008计算,群桩基础呈非整体破坏情况下,基桩桩长至少不小于下列哪一个选项?
A B C D
D
[解析] 该题考查内容为桩基抗浮承载力计算,计算抗拔侧阻力时,应注意乘以抗拔系数λ,桩身混凝土自重计算时应扣除水浮力,同时应注意题中给定的群桩基础呈非整体破坏的条件,根据《建筑桩基技术规范》JGJ 94—2008第5.4.5条,做如下计算:
(1)G
p=
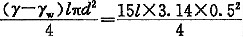
=2.94l
(2)T
uk=∑λ
iq
siku
il
i=0.8×50×3.14×0.5l=62.8l
(3)N
k≤T
uk/2+G
p,800≤62.8l/2+2.94l,800≤34.34l,l≥23.3m
基础的抗浮设计是当前实际工程中经常遇到的,而抗浮桩方案经常被采用。抗浮桩群桩基础的破坏形式分为整体破坏和非整体破坏两类,实际设计时,两种破坏形式均应验算。该题中已给定呈非整体破坏的条件,故只需验算一种情况就可以了。题中问题没有直接要求验算抗浮承载力,而是问需要的桩长,将桩长作为未知数,通过满足承载力要求的算式可解出桩长。
解题过程中有两点需要注意:①因抗拔极限侧阻力标准值与抗压极限侧阻力标准值不同,计算抗拔侧阻力时,应注意乘以抗拔系数λ;②基桩抗拔承载力时应计入桩身自重,但位于地下水位以下的桩身部分应扣除浮力后计入,同时应注意,因桩身自重属于有利于抗浮作用的一种恒载,故不需要像土对桩的侧阻力一样除以2后作为抗浮承载力特征值。
13. 某端承桩单桩基础桩身直径d=600mm,桩端嵌入基岩,桩顶以下10m为欠固结的淤泥质土,该土有效重度为8.0kN/m
3,桩侧土的抗压极限侧阻力标准值为20kfa,负摩阻力系数ξ
n为0.25,按《建筑桩基技术规范》JGJ 94—2008计算,桩侧负摩阻力引起的下拉荷载最接近于下列哪一选项?

- A.150kN
- B.190kN
- C.250kN
- D.300kN
A B C D
B
[解析] 该题考查内容为桩基负摩阻力计算,考点有两个,一个是中性点的确定;另一个是桩侧负摩阻力标准值的计算。据题中给出的嵌岩桩条件和欠固结的淤泥质土层厚度,确定中性点深度l
n;计算桩侧负摩阻力标准值时,需先计算欠固结的淤泥质土层的平均竖向有效应力,然后再乘以该土层负摩阻力系数。根据《建筑桩基技术规范》JGJ 94—2008第5.4.3条与第5.4.4条,计算如下:
(1)查表5.4.4-2,桩端嵌入基岩,l
n/l
o=1,l
n=l
o=10m
(2)

=

=40.0KPa
(3)
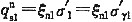
=0.25×40=10.0KPa<20KPa 取
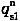
=10.0KPa
(4)

=3.14×0.6×10×10×=188.4KN
遇有下列条件时,桩周土层产生的沉降通常会超过基桩的沉降,计算基桩承载力时应计入桩侧负摩阻力:
(1)桩穿越较厚松散填土、自重湿陷性黄土、欠固结土、液化土层进入相对较硬土层时;
(2)桩周存在软弱土层,邻近桩侧地面承受局部较大的长期荷载,或地面大面积堆载(包括填土)时;
(3)由于降低地下水位,使桩周土有效应力增大,并产生显著压缩沉降时。
对于摩擦型基桩可取桩身计算中性点以上侧阻力为零;对于端承型基桩应计算负摩阻力引起基桩的下拉荷载
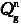
。当无实测资料时,可按《建筑桩基技术规范》JGJ 94—2008第5.4.3条与第5.4.4条规定计算。
14. 某建筑场地地层分布及参数(均为特征值)如图所示,拟采用水泥土搅拌桩复合地基。已知基础埋深2.0m,搅拌桩长8.0m,桩径600mm,等边三角形布置。经室内配比试验,水泥加固土试块强度为1.0MPa,桩身强度折减系数η=0.3,桩间土承载力折减系数β=0.6,按《建筑地基处理技术规范》JGJ 79—2002计算,要求复合地基承载力特征值达到100kPa,则搅拌桩间距宜取下列哪个选项?
A B C D
B
[解析] 按桩身侧摩阻力及桩端阻力计算:R
a=πd∑q
sil+αq
pA
p 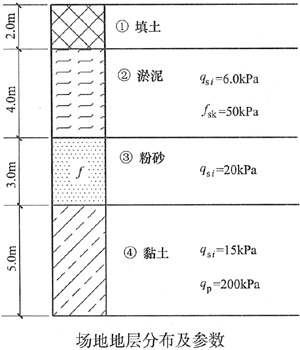
=3.14×0.6×(6.0×4.0+20.0×3.0+15.0×1.0)+(0.4~0.6)×200×3.14×0.3
2 =186.52+(0.4~0.6)×56.52
=209~220.43kN
如果忽略了系数α,则结果为243.04kN
桩身强度折减计算:
R
a=ηf
cuA
p=0.3×1.0×1000×3.14×0.3
2 =84.78kN
以上两者取小值,R
a=84.78kN
反算置换率:
m=
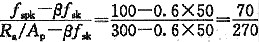
=25.9%
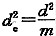
≈1.39,d
e=1.18m,s=1.18/1.05=1.12m
本题第一个考点是取用单桩承载力,从桩身强度折减计算和按桩身侧摩阻力及桩端阻力计算得到的单桩承载力中选用较小值。
根据题干中搅拌桩长为8.0m,基础埋深2.0m,考生应该能从图中得知搅拌桩顶位于淤泥层顶面,桩端进入黏土层1.0m,并从图中给出的各土层的侧阻力和黏土层的端阻力计算出单桩承载力,其中端阻力前乘以系数α是对的,不乘系数或系数取1.0也可以,不影响计算结果,计算时,可以忽略桩顶垫层厚度的影响。
第二个考点是根据计算出的单桩承载力按复合地基承载力公式求置换率,然后是按等边三角形布桩求桩间距。
本题是复合地基最基本的计算,工程师应该熟练掌握。
15. 某工程,地表淤泥层厚12.0m,淤泥层重度为16kN/m
3。已知淤泥的压缩试验数据如下表所示。地下水位与地面齐平。采用堆载预压法加固,先铺设厚1.0m的砂垫层,砂垫层重度为20kN/m
3,堆载土层厚2.0m,重度为18kN/m
3。沉降经验系数ξ取1.1,假定地基沉降过程中附加应力不发生变化,按《建筑地基处理技术规范》JGJ 79—2002估算淤泥层的压缩量最接近下列哪个选项?
压缩试验数据
| 压力p(kPa) | 12.5 | 25.0 | 50.0 | 100.0 | 200.0 | 300.0 |
| 孔隙比e | 2.108 | 2.005 | 1.786 | 1.496 | 1.326 | 1.179 |
A B C D
C
[解析] 根据规范第5.2.12条
淤泥层中点自重应力为:γh=(16-10)×6.0=36.0kPa
查表得相应孔隙比e
1=1.909
淤泥层中点自重应力与附加应力之和为:36.0+20×1.0+18×2.0=92.0kPa
查表得相应孔隙比e
2=1.542
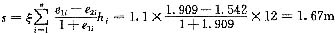
本题是根据室内压缩试验结果求固结沉降量,第一个考点是根据自重应力和附加应力求淤泥固结前后的孔隙比,注意水下应该用有效重度,根据应力大小在表中插值求得孔隙比;第二个考点是根据规范公式(5.2.12)求固结沉降量。
实际工程中,一般做起始压力为100kPa的压缩试验,如果该工程要做预压法加固,应该要求试验室做小起始压力的试验,才能满足沉降计算的要求,沉降经验系数ξ各个地区应该根据当地淤泥性质和工程经验选取,本试题在题于中建议选取1.1。
17. 砂土地基,天然孔隙比e
o=0.892,最大孔隙比e
max=0.988,最小孔隙比e
min=0.742。该地基拟采用挤密碎石桩加固,按等边三角形布桩,碎石桩直径为0.50m,挤密后要求砂土相对密度D
rl=0.886,问满足要求的碎石桩桩距(修正系数ξ取1.0)最接近下面哪个选项?
A B C D
C
[解析] 依据公式(8.2.2-1),S=0.95ξd·
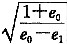
依据公式(8.2.2-3)先求上式中的e
1 e
1=e
max-D
rl(e
max-e
min)=0.988-0.886(0.988-0.742)=0.770
S=0.95×1.0×0.5×
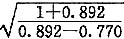
=0.95×1.0×0.5×3.938=1.87
取S≈1.80m
松散的砂土地基常用挤密碎石桩进行加固,挤密加固设计的控制指标是砂土的孔隙比,从天然孔隙比挤密到符合设计要求的孔隙比。因此本题第一个考点是根据规范公式(8.2.2-3),按题意挤密后要求达到的已知相对密度求挤密后的孔隙比;第二个考点就是根据规范公式(8.2.2-1),已知加固前后的孔隙比、砂石桩直径求桩间距。
本题是砂土挤密加固常见的基本计算,考生应知道相对密度的含义。
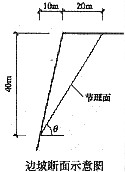
18. 某很长的岩质边坡的断面形状如图所示。岩体受一组走向与边坡平行的节理面所控制,节理面的内摩擦角为35°,黏聚力为70kPa,岩体重度为23kN/m
3。请验算边坡沿节理面的抗滑稳定系数最接近下列哪个选项?
A B C D
B
单位长度的不稳定岩体(即节理面以上岩体)体积V:V=1/2×20×40=400m
3/m
2.单位长度的滑面面积A:A=L=[(10+20)
2+40
2]
1/2=50m
2/m
3.不稳定岩体自重:W=V
γ=400×23=9200kN/m
4.节理面与水平方向间的夹角:θ=tan
-1(40/30)=53.1°
5.节理面上自重力的分解:垂直于节理面的力:N=Wcosθ=9200×cos53.1°=5524kN/m
平行于节理面的力:T=Wsinθ=9200×sin53.1°=7357kN/m
6.抗滑稳定安全系数:根据库仑公式,可以计算不稳定岩体沿节理面滑动的安全系数:
F
s=
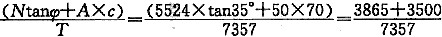
=1.0
直线(平面)滑动面是岩土体极限平衡分析中最简单的一种情况,由于它具有较强的实用性,计算量适中,能够反映岩土体破坏的基本机理,在注册岩土考试的案例题中成为最常见的题型之一。
直线(平面)滑动面常发生在无黏性土坡或者土工结构物中,也会发生在具有简单结构面的岩体中,以及各种构造物与岩土体间的界面处。其计算分析涉及岩土力学中最基本原理之一——摩尔—库仑强度准则,具体的应用是库仑公式:
τ
f=c+σ
ntanφ
两侧乘以滑动面面积,则变成:
S=cA+Ntanφ
此题是一种最简单的情况,在掌握了其基本原理以后,关键在于几何角度和尺寸的计算以及力的分解。由于一些从事设计的工程技术人员平时总是使用软件,或者使用规范的现成公式计算,基本计算能力下降,常有计算错误或者超时的情况。所以对于力的分解、几何尺寸换算和静力平衡等基本计算要多练习,更熟练。
19. 一个坡角为28°的均质土坡,由于降雨,土坡中地下水发生平行于坡面方向的渗流,利用圆弧条分法进行稳定分析时,其中第i条块高度为6m,作用在该条块底面上的孔隙水压力最接近于下面哪一数值?

- A.60kPa
- B.53kPa
- C.47kPa
- D.30kPa
A B C D
C
[解析] 如下图,由于产生沿着坡面的渗流,坡面线为一流线,过第i条底部中点的等势线为ab线,以过a点的水平线为基线,由于同一等势线上的总水头相等,b点的位置水头为ad=h
w,压力水头为0,a点的位置水头为0,则压力水头为h
w,水头高度h
w为:
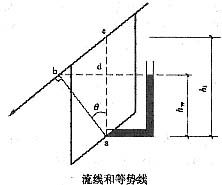
h
w=
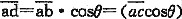
cosθ=h
icos
2θ=6cos
228°=4.68m
孔隙水压力=h
w·γ
w=4.68×10=46.8kPa
这道题的考点就在于渗流。土中水的渗流是土力学理论和土工实践中的一个基本课题。除在水利水电工程领域外,对其他各种土木工程行业也都是十分重要的。在稳定渗流中,绘制流网是简单可靠的方法。可用它确定渗流场中的渗流的流速、压力和水力梯度的分布,分析土体的稳定性和变形。
在静水位以下,各点的总势能都是相等的,亦即其重力势(位置水头)与压力势(压力水头)之和是相等的,所以自上而下水压力是线性分布的。而在稳定渗流情况下,需要确定等势线,在同一等势线上,各点的重力势(位置水头)与压力势(压力水头)之和是相等的,因而等势线是确定孔隙水压力的关键。
此题的解决,首先根据条件确定流线,由于是沿坡渗流,所有的流线都平行于坡面线,根据正交性,等势线必须垂直于流线,那么过此土条中点a的等势线为ab,如果以a点的位置水头为0,则b点的位置水头为ad=ab×cos28°,其中ab=ac×cos28°=6×cos28°,则h
w=ad=6×cos
228°=4.68m。
20. 重力式挡土墙墙高8m,墙背垂直、光滑,填土与墙顶平,填土为砂土,γ=20kN/m
3,内摩擦角φ=36°该挡土墙建在岩石边坡前,岩石边坡坡脚与水平方向夹角为θ=70°,岩石与砂填土间摩擦角为18°计算作用于挡土墙上的主动土压力最接近于下列哪个数值?
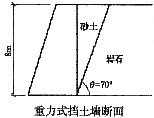
- A.166kN/m
- B.298kN/m
- C.157kN/m
- D.213kN/m
A B C D
B
[解析] 楔体自重W=γV=20×
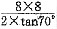
=233kN/m E
a=Wtan52°=298kN/m
这是一种墙后填土受限的情况,亦即填土的范围小于根据朗肯或库伦土压力确定的滑动面。这时不能直接套用这些土压力理论的公式计算主动(或被动)土压力,而是通过实际上可能的滑动面计算最大(或最小)土压力,作为主动(或被动)土压力。
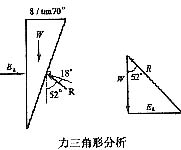
在这道题中,墙背垂直、光滑,填土与墙顶平,符合朗肯土压力理论的使用条件。但岩体界面与水平向间的夹角为70°,大于根据朗肯土压力理论的45°+φ/2=63°,并且岩土之间的摩擦角δ
R又小于砂土韵内摩擦角φ,因而对应于最大土压力的滑动面不可能在土体内部,而是在岩土间的界面。
如果用朗肯土压力理论计算:
K
a=tan
2(45°-φ/2)=tan
227°=0.26
E
a=
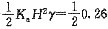
×64×20=166kN/m
可见它远比298kN/m要小,因为主动土压力是所有对应的滑动面中产生最大土压力的情况,所以E
a=Wtan52°=298kN/m是解答。
在这类问题中,如果砂土之后是原状的黏土(如题图所示),这时墙上的主动土压力需要经过搜索才能确定。亦即分别假定滑动面通过砂土、黏土和界面,找到最大土压力则为主动土压力。可见这种解决方法,实际上是库伦土压力理论方法,亦即考虑滑动土体的楔体平衡。尽管“墙背垂直、光滑,填土与墙顶平”,似乎符合朗肯土压力理论的使用条件。
有人常常对自己的计算能力没有信心,偏爱规范。对于类似的问题,《建筑边坡工程技术规范》GB 50330—2002的式(6.2.8-1)也可以使用。

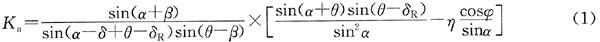
式中
η=
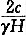
(2)
对于题20,式(1)中:β=0°,α=90°,δ=0°,δ
R=18°,θ=70°,η=0°
将上面这些参数代入式(1),就可以计算出:
K
a=
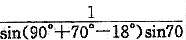
×
sin(90°+70°)sin(70°-18°)=0.467
E
a=K
aH
2γ/2=0.467×64×20/2=298kN/m
可见结果是一样的,但这种一切计算都必须找到规范的做法是不应提倡的,除非考题指定规范外,能够用土力学基本原理解决的,应尽量自己解决,不要过分依赖规范。
22. 在饱和软黏土地基中开挖条形基坑,采用8m长的板桩支护。地下水位已降至板桩底部。坑边地面无荷载。地基土重度为γ=19kN/m
3。通过十字板现场测试得地基土的抗剪强度为30kPa。按照《建筑地基基础设计规范》GB50007—2002规定,为满足基坑抗隆起稳定性要求,此基坑最大开挖深度不能超过下列哪一个选项?
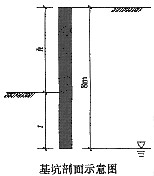
A B C D
B
[解析] 根据《建筑地基基础设计规范》GB 50007—2002附录V,
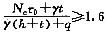
,τ
o=c
u=30kPa,N
c=5.14,q=0.h+t=8m
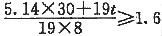
,19t≥89,t=4.68m,h=3.32m
关于软黏土基坑坑底隆起的验算各种规范基本都是用坑底地基土的承载力进行的,但是所用的承载力理论和土的强度指标不尽相同。《建筑地基基础设计规范》GB 50007—2002附录V给出的公式(V.0.1)属于普朗特尔—瑞斯纳(Prandtl-Reissner)公式,即对于φ
u,=0°的饱和软黏土,N
c=2+π=5.14,N
q=1.0。
此题的命题有一个特点,那就是反向的问题。它不是要你按照给定的条件用式(V.0.1)计算基坑坑底隆起的安全系数,而是“按照《建筑地基基础设计规范》GB 50007—2002规定”计算基坑最大开挖深度。而所谓的“规定”就是
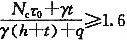
,亦即按规范的规定取抗隆起安全系数K
h=1.6。在注册考试的考题中经常有这种逆向思考与计算的情况,应特别注意。
23. 基坑锚杆拉拔试验时,已知锚杆水平拉力T=400kN,锚杆倾角α=15°,锚固体直径D=150mm,锚杆总长度为18m,自由段长度为6m。在其他因素都已考虑的情况下,锚杆锚固体与土层的平均摩阻力最接近下列哪个数值?
- A.49kPa
- B.73kPa
- C.82kPa
- D.90kPa
A B C D
B
[解析] 锚固段长度:l=18-6=12m
轴向拉力:N=
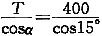
=414KN
锚固体与土层的平均摩阻力:
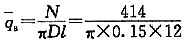
=73KPa
这也是一道反算的考题,即已知锚杆水平拉力反算锚固体与地基土间的平均摩阻力。需注意的是,考题给出的是水平拉力T,要通过N=
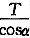
计算锚杆的轴向力N。如果直接采用T计算虽然也可选择答案(B),但那是错误的答案,当然在试卷复审时是不会给分的。
由于计算量较小,基本概念简单清楚,类似此题的锚杆方面的考题,几乎每年都有。这个试验结果的解题过程并不涉及规范,根据土力学的基本概念即可求解,试验时所施加的荷载是标准值,极限状态时起控制作用的一般是锚固体与岩土体间的极限摩阻力,基本公式为
N
u,k=πDm∑q
sikL
i式中 N
u,k——锚杆轴向抗拔极限承载力标准值;
L
i——锚杆在第i层土层中的锚固段长度;
D
m——锚固体直径;
q
sik——锚固段与第i层土层间的极限摩阻力。
以前的规范中,对锚杆的设计,有采用分项系数方法的,锚杆的拉力和锚固体的抗拔力都采用设计值;近年来出版与修订的有些规范,设计方法采用定值设计的安全系数法,荷载组合采用标准值,即锚杆的拉力采用标准值;锚固体的抗拔力也采用标准值,即极限值除以安全系数,其值为:N
k=N
uk/K
t,K
t为锚固体拉拔安全系数。
25. 斜坡上有一矩形截面的岩体,被一走向平行坡面、垂直层面的张裂隙切割至层面(如图所示),岩体重度γ=24kN/m
3,层面倾角α=20°,岩体的重心铅垂延长线距O点d=0.44m,在暴雨充水至张裂隙顶面时,该岩体倾倒稳定系数K最接近下列哪一选项?(不考虑岩体两侧及底面阻力和扬压力)
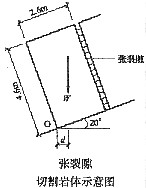
A B C D
B
[解析] 从下图所示可知,岩体重力ω是抗倾覆力,张裂隙中的静水压力f是倾覆力,岩体倾覆稳定系数为:
K=
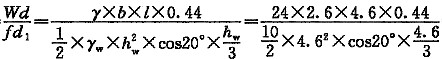
=0.83
该题的考点为倾覆稳定系数的概念,倾覆稳定系数为抗倾覆力矩和倾覆力矩的比值。
在本题中,由于不考虑岩体两侧及底面阻力和扬压力,倾覆力只有张裂隙中的静水压力f,岩体重力ω是抗倾覆力。解题的关键点在于张裂隙中静水压力的计算,须注意,张裂隙底部的水头高度是h
wcos20°,而不是h
w。因此静水压力值为γ
wh
wcos20°而非γ
wh
w,其中h
w为题图中给出的4.6m。
26. 如图所示,边坡岩体由砂岩夹薄层页岩组成,边坡岩体可能沿软弱的页岩层面发生滑动。已知页岩层面抗剪强度参数c=15kPa,φ=20°,砂岩重度γ=25kN/m
3。设计要求抗滑安全系数为1.35,问每米宽度滑面上至少需增加多少法向压力才能满足设计要求?
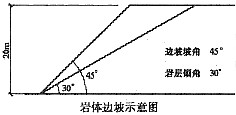
- A.2180kN
- B.1970kN
- C.1880kN
- D.1730kN
A B C D
B
[解析] 取1m宽度计算:
①滑体体积V=
×20×20(cot30°-cot45°)=146.4m
3 ②滑体重量W=γV=25×146.4=3660kN
③假设施加法向力f
F=
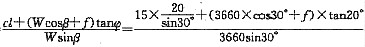
=1.35
f=1969KN
本题为平面滑动问题,下滑力为重力沿滑面的分量,抗滑力取决于滑面处的抗剪强度,符合库仑定律,即:τ=σtanφ+c。增加坡面正压力是提高坡面抗滑强度的重要手段,此时的正压力由重力垂直坡面的分量(ω·cosβ)和所施加的正压力(f)两部分组成。依次计算即可得到正确答案。注意在计算中不要忘记沿滑面分布的黏聚力的作用。
27. 某黄土试样的室内双线法压缩试验数据如下表所示。其中一个试样保持在天然湿度下分级加荷至200kPa,下沉稳定后浸水饱和;另一个试样在浸水饱和状态下分级加荷至200kPa。按此表计算黄土湿陷起始压力最接近下列哪个选项的数据?
室内双线法压缩试验数据
| 压力p(kPa) | 0 | 50 | 100 | 150 | 200 | 200浸水饱和 |
天然湿度下试样高度
hp(mm) | 20.00 | 19.79 | 19.53 | 19.25 | 19.00 | 18.60 |
|
浸水饱和状态下试样高度 (mm) (mm) | 20.00 | 19.58 | 19.26 | 18.92 | 18.60 | |
- A.75kPa
- B.100kPa
- C.125kPa
- D.150kPa
A B C D
C
[解析] 根据《湿陷性黄土地区建筑规范》GB 50025—2004第2.1.8条、4.3.5条及条文说明,湿陷起始压力下
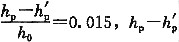
=0.015×20=0.3mm
当p=100kPa时,h
p-
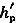
=0.27mm。当p=150kPa时,h
p-
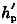
=0.33mm。
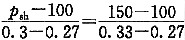
,p
sh=125kPa
规范规定湿陷起始压力为湿陷性黄土浸水饱和,开始出现湿陷时的压力。而又把湿陷系数δ
s=0.015作为判定黄土湿陷的界限标准。据此标准,并根据双线法压缩试验记录的各级压力和相应压力下的天然状态下与浸水饱和状态下的试样高度之差(在湿陷起始压力附近)呈直线关系,因此可以用内插的方法确定黄土的湿陷起始压力。
30. 某灌注桩,桩径1.2m,桩长60m,采用声波透射法检测桩身完整性,两根钢制声测管中心间距为0.9m,管外径为50mm,壁厚2mm,声波探头外径28mm。水位以下某一截面平测实测声时为0.206ms,试计算该截面处桩身混凝土的声速最接近下列哪一选项?
[注:声波探头位于测管中心;声波在钢材中的传播速度为5420m/s,在水中的传播速度为1480m/s;仪器系统延迟时间为0s。]
- A.4200m/s
- B.4400m/s
- C.4600m/s
- D.4800m/s
A B C D
B
[解析] (1)声波在钢管中的传播时间
t
刚=
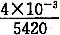
=0.738×10
-6s
(2)声波在水中的传播时间
t
水=
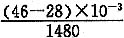
=12.162×10
-6s
(3)声波在钢管中和水中的传播时间之和
t'=t
钢+t
水=12.900×10
-6s=12.900×10
-3ms
(4)两个测管外壁之间的净距离
l=0.9-0.05=0.85m
(5)声波在混凝土中的传播时间
t
ci=0.206-0-12.900×10
-3=0.1931ms=1.931×10
-4s
(6)该截面混凝土声速
υ
i=
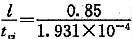
=4402m/s
声波透射法也是桩身混凝土介质状况检测的一种方法,尤其对于大直径超长桩。此题主要考查考生对声波在检测过程中如何传播和混凝土声速计算的掌握情况。
根据题干,声波在各种介质(钢管、水、混凝土)中的传播距离是已知或可以计算出来的,也告诉了声波在钢材中的传播速度为5420m/s,在水中的传播速度为1480m/s,这样就可以计算出来声波在钢材中、水中和混凝土中的传播时间,从而计算出混凝土中的声速。解题时需要注意:①题干中告知声波探头位于测管中心;②题干中告知仪器系统延迟时间为0s;③声波传播距离与时间单位的换算。
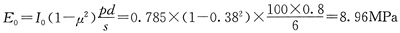
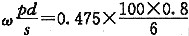 =6.33MPa
=6.33MPa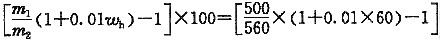 ×100=42.9%
×100=42.9%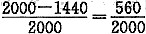 =28%,大于25%,属混合土;
=28%,大于25%,属混合土;
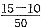 =0.1
=0.1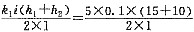 =6.25m3/d
=6.25m3/d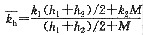 =17.86m/d
=17.86m/d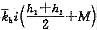 ×1=17.86×0.1×17.5=31.25m3/d
×1=17.86×0.1×17.5=31.25m3/d =1.0,
=1.0,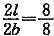 =1.0,查表得αo=0.336
=1.0,查表得αo=0.336 ×0.336×400=33.6kPa
×0.336×400=33.6kPa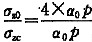 =4
=4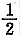 l和
l和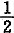 面积下的角点的
面积下的角点的
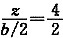 =2,
=2,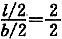 =1,查表得
=1,查表得 =0.084
=0.084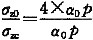 =4
=4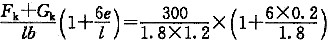 =231.48KPa
=231.48KPa
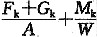
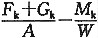
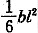
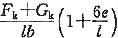
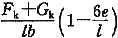
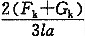
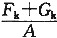 计算 pk=fa时的基底面积
计算 pk=fa时的基底面积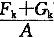 其中 Gk=γGdA
其中 Gk=γGdA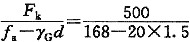 =3.62m2 答案B。
=3.62m2 答案B。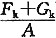 =fa
=fa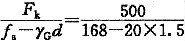 =3.62m2
=3.62m2
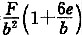 =700/2.42×(1+6×0.125/2.4)
=700/2.42×(1+6×0.125/2.4)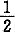 ×0.45×(2.4+2.4-2×0.45)=139.96kN
×0.45×(2.4+2.4-2×0.45)=139.96kN
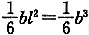 代入上式,得 pjmax=
代入上式,得 pjmax=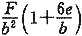
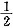 ×0.45×(2.4+2.4-2×0.45)
×0.45×(2.4+2.4-2×0.45)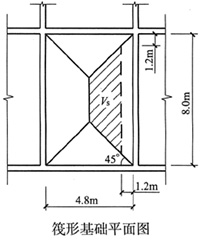

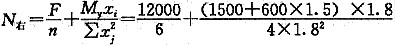 =2333KN
=2333KN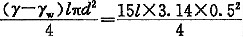 =2.94l
=2.94l
 =
= =40.0KPa
=40.0KPa 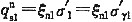 =0.25×40=10.0KPa<20KPa 取
=0.25×40=10.0KPa<20KPa 取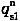 =10.0KPa
=10.0KPa =3.14×0.6×10×10×=188.4KN
=3.14×0.6×10×10×=188.4KN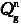 。当无实测资料时,可按《建筑桩基技术规范》JGJ 94—2008第5.4.3条与第5.4.4条规定计算。
。当无实测资料时,可按《建筑桩基技术规范》JGJ 94—2008第5.4.3条与第5.4.4条规定计算。
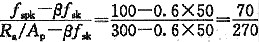 =25.9%
=25.9%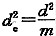 ≈1.39,de=1.18m,s=1.18/1.05=1.12m
≈1.39,de=1.18m,s=1.18/1.05=1.12m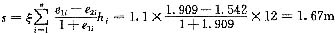
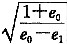
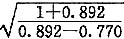 =0.95×1.0×0.5×3.938=1.87
=0.95×1.0×0.5×3.938=1.87
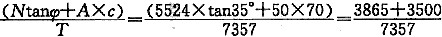 =1.0
=1.0

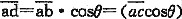 cosθ=hicos2θ=6cos228°=4.68m
cosθ=hicos2θ=6cos228°=4.68m
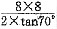 =233kN/m Ea=Wtan52°=298kN/m
=233kN/m Ea=Wtan52°=298kN/m
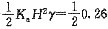 ×64×20=166kN/m
×64×20=166kN/m
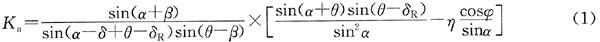
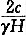 (2)
(2)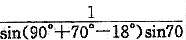 ×
×
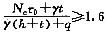 ,τo=cu=30kPa,Nc=5.14,q=0.h+t=8m
,τo=cu=30kPa,Nc=5.14,q=0.h+t=8m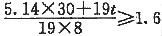 ,19t≥89,t=4.68m,h=3.32m
,19t≥89,t=4.68m,h=3.32m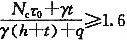 ,亦即按规范的规定取抗隆起安全系数Kh=1.6。在注册考试的考题中经常有这种逆向思考与计算的情况,应特别注意。
,亦即按规范的规定取抗隆起安全系数Kh=1.6。在注册考试的考题中经常有这种逆向思考与计算的情况,应特别注意。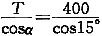 =414KN
=414KN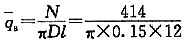 =73KPa
=73KPa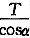 计算锚杆的轴向力N。如果直接采用T计算虽然也可选择答案(B),但那是错误的答案,当然在试卷复审时是不会给分的。
计算锚杆的轴向力N。如果直接采用T计算虽然也可选择答案(B),但那是错误的答案,当然在试卷复审时是不会给分的。
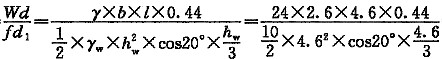 =0.83
=0.83
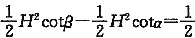 ×20×20(cot30°-cot45°)=146.4m3
×20×20(cot30°-cot45°)=146.4m3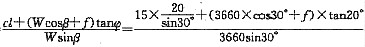 =1.35
=1.35 (mm)
(mm)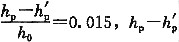 =0.015×20=0.3mm
=0.015×20=0.3mm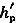 =0.27mm。当p=150kPa时,hp-
=0.27mm。当p=150kPa时,hp-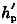 =0.33mm。
=0.33mm。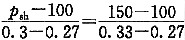 ,psh=125kPa
,psh=125kPa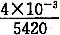 =0.738×10-6s
=0.738×10-6s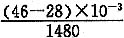 =12.162×10-6s
=12.162×10-6s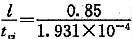 =4402m/s
=4402m/s