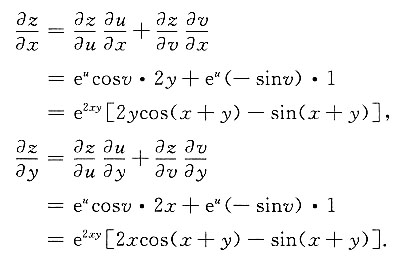一、单项选择题2. 设函数f(x)在x
0处可导,则
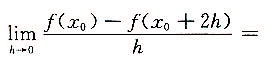
______
A.2f'(x
0)
B.-2f'(x
0)
C.
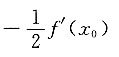
D.
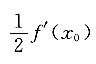
A B C D
B
[解析] 因为
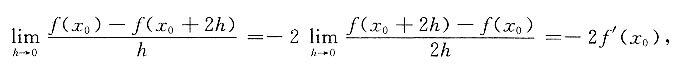
故应选B.
3. 设函数f(xy,x-y)=x
2+y
2,则

______
- A.2x+2y
- B.2+2y
- C.2x-2y
- D.2-2y
A B C D
B
[解析] 因为f(xy,x-y)=x
2+y
2=(x-y)
2+2xy,所以f(x,y)=y
2+2x,
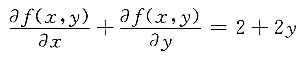
,故应选B.
5. 5人排成一行,甲、乙两人排在一起的概率P=______
A.
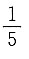
B.

C.
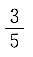
D.
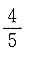
A B C D
B
[解析] 事件总数为
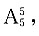
甲、乙两人排在一起的事件总数为
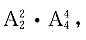
因此甲、乙两人排在一起的概率

.故应选B.
二、填空题1. 设y=sin(lnx
2),则y'=______.
[解析]
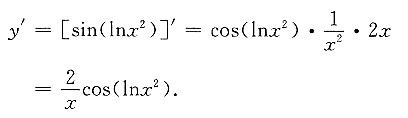
2. 若函数
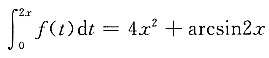
,则f(x)=______.
3. 函数f(x)=x
3-27x+2在[0,1]上的最大值为______.
2
[解析] 因为f'(x)=3x2-27,
当0<x<1时,f'(x)<0,所以,f(x)在[0,1]上单调减少,最大值为f(0)=2.
4. 曲线
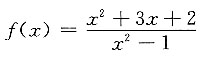
的垂直渐近线有______条.
1
[解析] 因为
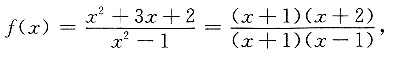
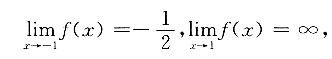
只有x=1一条垂直渐近线.
5.
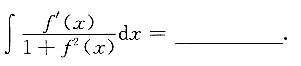
arctanf(x)+C
[解析]

6. 设z=e
-x-(x-2y)tan(xy),则
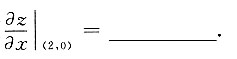
-e-2
[解析] z(x,0)=e
-x,所以
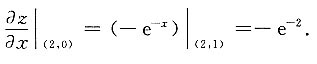
7. 已知E(X)=-1,D(X)=3,则E[3(X
2-2)]=______.
6
[解析] E(X2)-[E(X)]2=D(X),即E(X2)=[E(X)]2+D(X)=(-1)2+3=4,E[3(X2-2)]=3E(X2-2)=3E(X2)-3·2=12-6=6.
8. 设A,B为三阶方阵,|A|=4,AB=E,则|B|=______.
[解析] 由题意可知,AB=E,则|AB|=|A||B|=|E|,即4·|B|=1,
故
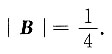
9. 以y=C
1e
-3x+C
2xe
-3x为通解的二阶常系数齐次线性微分方程为______.
y"+6y'+9y=0
[解析] 由y=C1e-3x+C2xe-3x为通解知,特征方程有二重特征根r=-3,特征方程为(r+3)2=0,即r2+6r+9=0,所以微分方程为y"+6y'+9y=0.
10. 点M(3,2,-1)到平面x+y+z-1=0的距离为______.
[解析]
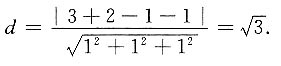
三、解答题1. 求极限
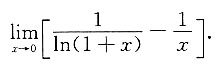
2. 已知
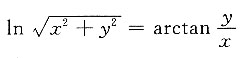
确定y是x的函数,求
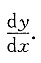
方程两边对x求导,得
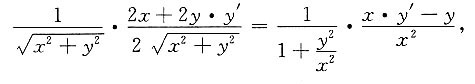
整理,得x+y·y'=x·y'-y,
从而
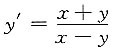
,所以

3. 求定积分
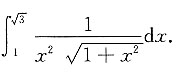
4. 设成本函数C(Q)=54+18Q+6Q
2,试求平均成本最低时的产量.
平均成本为
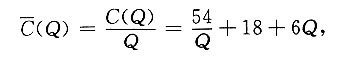
对其求导数,得
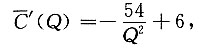
令
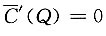
,得Q=3;由
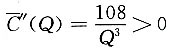
,所以Q=3是平均成本
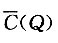
的极小值点,也就是平均成本最低时的产量.
5. 在曲面z=xy上求一点,使这点处的法线垂直于平面x+3y+z+9=0,并写出法线方程.
设所求点为M(x
0,y
0,z
0),
曲面在该点处的法线的方向向量为n={y
0,x
0,-1),平面的法向量为{1,3,1),
按题意,有
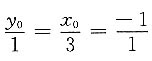
,求得x
0=-3,y
0=-1,
z
0=x
0y
0=3,所以所求点为(-3,-1,3),
法线方程为
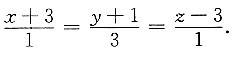
6. 计算
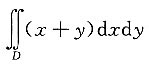
,其中D是由x+y=1,x-y=1及x=0所围成的区域.
积分区域如图所示,

则D={(x,y)|0≤x≤1,x-1≤y≤1-x},
所以
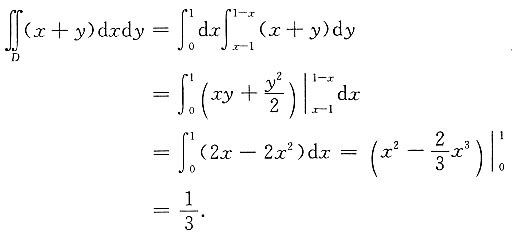
7. 求微分方程y"-4y'+13y=0满足初始条件y|
x=0=0,y'|
x=0=3的特解.
特征方程为r
2-4r+13=0,
解得特征根为r
1,2=2±3i,
故方程的通解为y=e
2x(C
1cos3x+C
2sin3x),
且有y'=e
2x[(2C
1+3C
2)cos3x+(2C
2-3C
1)sin3x],
代入初始条件得
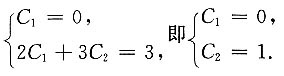
所以所求特解为y=e
2xsin3x.
8. 求向量组α
1=(1,0,-1,0),α
2=(0,1,1,2),α
3=(2,3,5,8),α
4=(1,1,-2,1)的秩和极大无关组.
将向量组写成列向量的形式构成的矩阵为

因此可知A的列秩为3,即α
1,α
2,α
3,α
4的秩为3,且A的极大无关组为α
1,α
2,α
3或α
1,α
2,α
4.
9. 求线性方程组
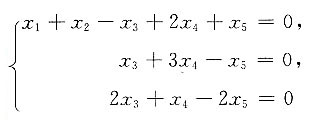
的通解.
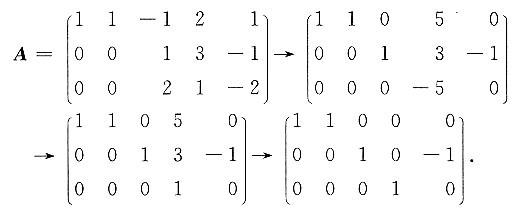
同解方程组为
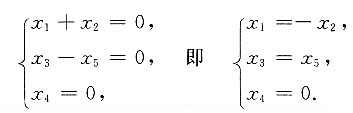
分别取x
2=1,x
5=0和x
2=0,x
5=1可得基础解系
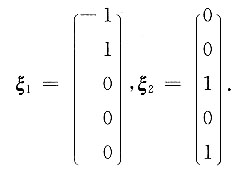
于是,线性方程组的通解为ξ=k
1ξ
1+k
2ξ
2,k
1,k
2为任意常数.
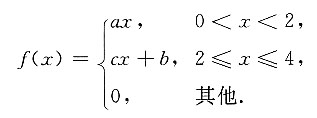
已知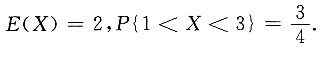 求:
求:10. a,b,c;
由
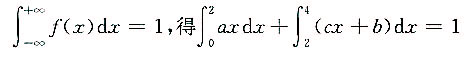
,即
2a+6c+2b=1. ①
由E(X)=2,得
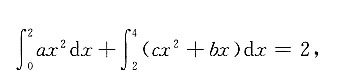
即
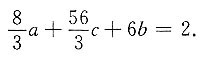
②
由
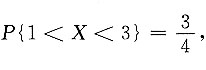
得
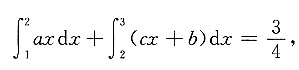
即

③
解①②③联立的方程组得:
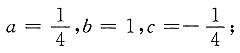
12. 设z=e
ucosy,u=2xy,v=x+y,求
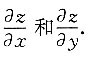
由复合函数求偏导数法则,得