一、单项选择题3. 若f(u)可导,且y=f(ln
2x),则
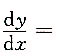
______
A.f'(ln
2x)
B.2lnx·f'(ln
2x)
C.
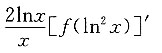
D.
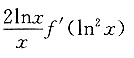
A B C D
D
[解析] 利用复合函数求导方法,得
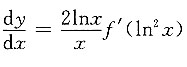
,故选D.
4. 设函数y=y(x)由参数方程
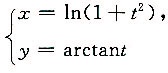
确定,则
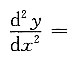
______
A.
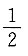
B.
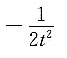
C.
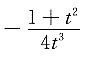
D.
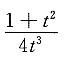
A B C D
C
[解析]
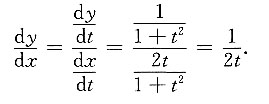
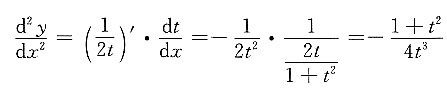
,应选C.
7. 若积分
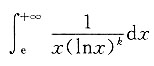
收敛,则k满足______
A B C D
A
[解析] 当k≠1时,
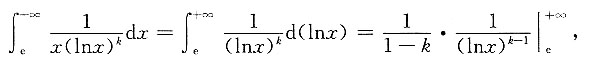
要使该积分收敛,则
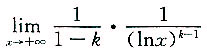
存在,故k>1;
当k=1时,
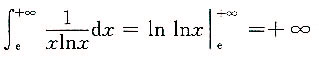
,积分发散.故选A.
8. 设z=ln(x
2+y
2),则
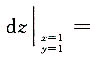
______
A.dx+dy
B.2xdx+2ydy
C.2dx+2dy
D.
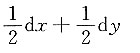
A B C D
A
[解析] 因为
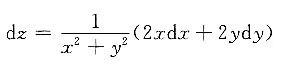
,所以
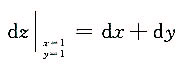
.故应选A.
9. 设y
1,y
2是微分方程y"+p(x)y'+q(x)y=0的两个解,则y=C
1y
1+C
2y
2(C
1,C
2为任意常数)是______
- A.该方程通解
- B.该方程的解
- C.该方程的特解
- D.不一定是方程的解
A B C D
B
[解析] 由二阶线性齐次微分方程的解的结构知y=C1y1+C2y2只能说是方程的解,不能保证为通解,故应选B.
二、填空题1. 设f(x)=2x+5,则f
-1[f(x)-1]=______.
[解析] 因为
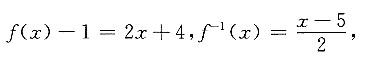
所以
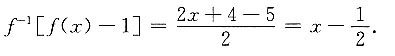
2. 若函数
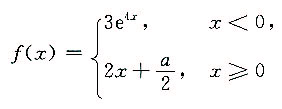
在x=0处连续,则a=______.
3.
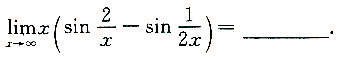
[解析]
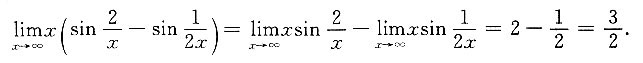
4. 函数f(x)=x
4-2x
2+5在
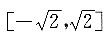
上的最大值为______.
5
[解析] f'(x)=4x
3-4x,令f'(x)=0得x=0,-1,1,
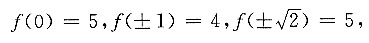
从而f(x)在
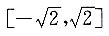
上的最大值为5.
5. 设f(x)=x(x+1)(x+2)…(x+2015),则f'(0)=______.
2015!
[解析]
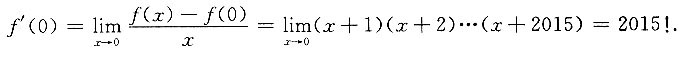
6. 曲线y=xe
-x的拐点是______.
(2,2e-2)
[解析] 因为y'=(1-x)e-x,y"=(x-2)e-x,令y"=0得x=2,
当x<2时,y"<0,当x>2时,y">0,
故拐点坐标为(2,2e-2).
7.
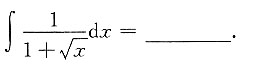
[解析]
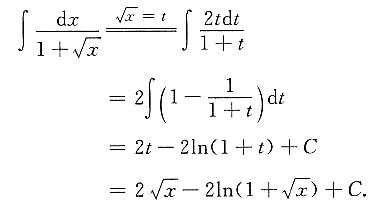
8. 当x>1时,有
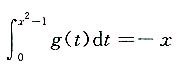
,且g(x)是连续函数,则g(3)=______.
[解析] 两边求导得g(x
2-1)·2x=-1,
即

取x=2,得
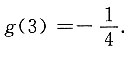
9. 已知a={-1,1,2},b={3,0,4),则a在b上的投影为Prj
ba=______.
1
[解析] a在b上的投影为
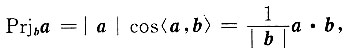
而
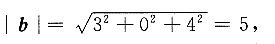
a·b=(-1)·3+1×0+2·4=5,
因此Prj
ba=1.
10. 设
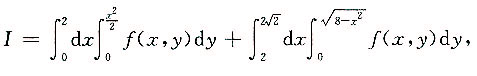
则交换积分次序后,I可以化为______.
[解析] 画出积分区域如图.
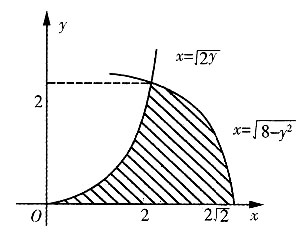
交换积分次序得
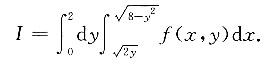
三、解答题1. 已知
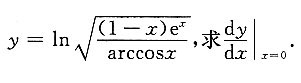
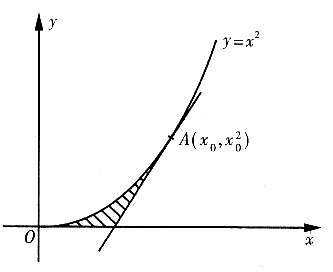
2. 过曲线y=x
2(x≥0)上某点A作切线,若切线、曲线、z轴围成的面积为
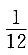
,求该图形绕x轴旋转一周所得旋转体的体积.
设A点坐标为
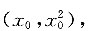
由y'=2x得切
线方程为
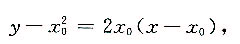
即
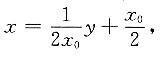
由
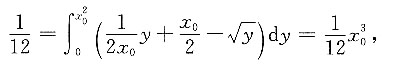
得x
0=1,切点A(1,1).
切线方程为2x-y-1=0,
切线与x轴交点为
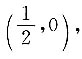
所求旋转体的体积
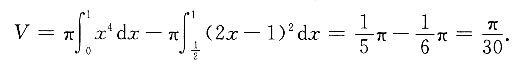
3. 求过点(2,-1,3)与直线
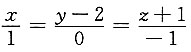
垂直,又与平面4x+3y=0平行的直线方程.
因为s
1={1,0,-1),n={4,3,0},
由题设知所求直线的方向向量
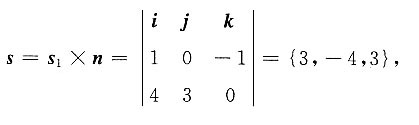
又因直线过点(2,-1,3),所以所求直线方程为
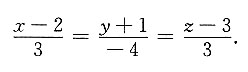
4. 设z=f(e
xsiny,ln(x+y)),其中,f(u,v)为可微函数,求
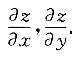
设u=e
xsiny,v=ln(x+y),则z=f(u,v),
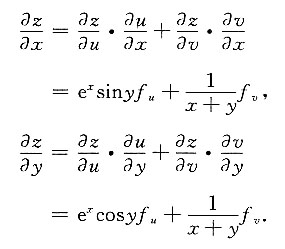
5. 求
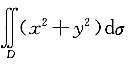
,其中D为y=x,y=x+a,y=a和y=3a(a>0)为边的平行四边形.
首先画出积分区域D.把它看作Y型.则
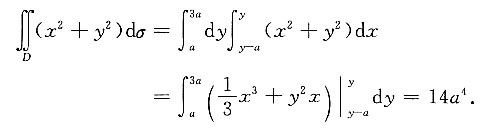
6. 求微分方程y'+ycosx=e
-sinx满足初始条件y(0)=-1的特解.
微分方程的通解为
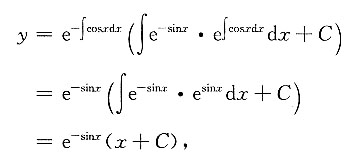
又y(0)=-1,即-1=e
-sin0(0+C),得C=-1,
所以所求特解为y=e
-sinx(x-1).
7. 将函数
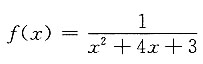
展开成(x-1)的幂级数.