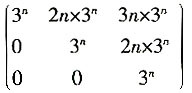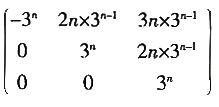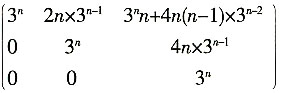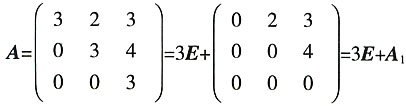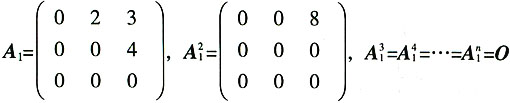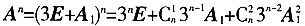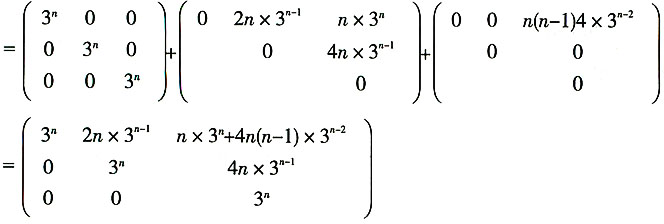一、单项选择在每小题给出的4个选项中,只有1项正确。2. 已知x为实数,且
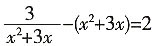
,那么x
2+3x的值为______。
A B C D
A
[解析] 设y=x
2+3x,则原方程变为
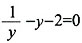
,即y
2+2y-3=0,解得y
1=1,y
2=-3,又因
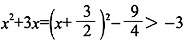
,故舍去-3,x
2+3x等于1,故正确答案为A。
4. 已知等比数列{a
n)的公比q>1(n∈N),第17项的平方等于第24项,则使
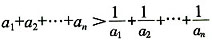
成立的n的取值范围为______。
A B C D
C
[解析] 由已知
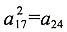
,知(a
1q
16)
2=a
1q
23。
因q>1,a
1≠0,得a
1=q
-9。
又

,故
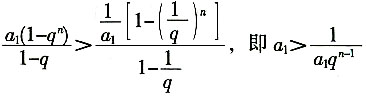
将a
1=q
-9代入得q
-18>q
1-n,n>19且n∈N。
故C为正确答案。
5. (3-2x)
4的二项展开式中,x
2项的系数是______。
A B C D
D
[解析] 由二项式定理,(3-2x)
4的二项展开式的第k项为
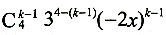
,令x
k-1=x
2,得k=3,
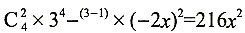
,于是x
2项的系数为216,故选D。
6. 计划展出10幅不同的画,其中1幅水彩画、4幅油画、5幅国画,排成一行陈列,要求同一品种的画必须连在一起,且水彩画不能放在两端,那么不同的陈列方法有______种。
A.
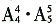
B.
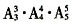
C.
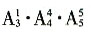
D.
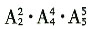
A B C D
D
[解析] 将油画、国画分别看作整体,有
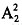
种排法,而油画内有
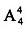
种排法,国画内有
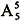
种排法,故共有
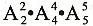
种排法,故选D。
7. 已知(x+i)
3是一个实数,则实数x=______。
A.
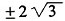
B.
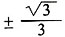
C.
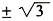
D.
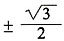
A B C D
B
[解析] (x+i)
3=x
3+3x
2i+3xi
2+i
3=(x
3-3x)+i(3x
2-1)它是一个实数,所以3x
2-1=0,即
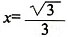
或
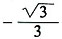
,故选B。
8. 在△ABC中,若c-a等于AC边上的高h,则
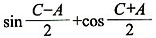
等于______。
A.-1
B.
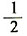
C.
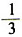
D.1
A B C D
D
[解析]
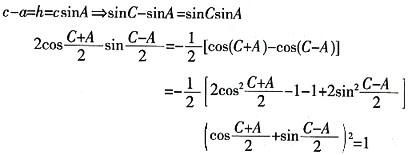
又c-a>0,故C>A,

,选D。
9. 把x-2y+c=0按向量a=(-1,2)平移,得到的直线与圆x
2+y
2+2x-4y=0相切,则c等于______。
A.
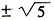
B.10或0
C.±5
D.13或5
A B C D
C
[解析] x′=x+1 y′=y+2,直线方程变为(x+1)-2(y-2)+c=0,即x-2y+5+c=0, 由
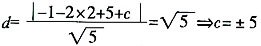
,故选C。
11. 设x→0时,e
x2-(ax
2+bx+c)是比x
2高阶的无穷小,其中a,b,c是常数,则______。
- A.a=1,b=2,c=0
- B.a=c=1,b=0
- C.a=c=2,b=0
- D.a=b=1,c=0
A B C D
B
[解析] 由题设
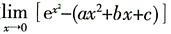
,所以c=1。
又因为
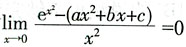
即
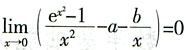
要使上式成立,需b=0,a=1,因此选B。
12. 已知,圆的周长为6π,则夹角60°的扇形的面积为______。
A.

B.π
C.
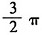
D.2π
A B C D
C
[解析] 设圆的半径为r,则由l=2πr,得r=3,于是圆的面积A=πr
2=9π。
故所求扇形的面积为
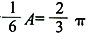
,C为正确答案。
13.
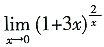
=______。
A B C D
D
[解析] 本题考查重要极限
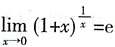
,对函数
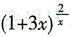
进行适当变形,利用公式
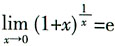
即可完成。
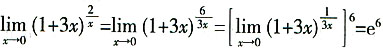
故D为正确答案。
14. 设
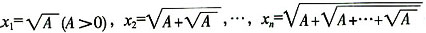
,则
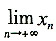
=______。
A.

B.
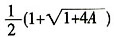
C.
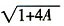
D.
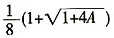
A B C D
B
[解析] (1)先证{x
n}单调增加
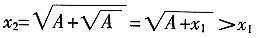
,假设当n=k时,有x
k>x
k-1,那么由A+x
k>A+x
k-1,知

,即x
k+1>x
k,故对任意的n=k+1,有x
n>x
n-1成立,由数学归纳法知{x
n}单调增加。
(2)再证数列{x
n)有上界
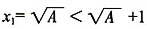
,设当n=k时,有
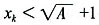
,那么当n=k+1时,
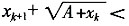
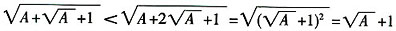
,因此有上界,从而{x
n}单调递增有上界,由单调有界定理知{X
n}收敛。
(3)再求
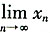
设
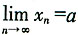
,对
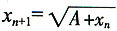
两端取极限,得
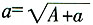
,解得
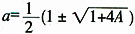
,由(1)知a>0,因此
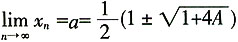
,故选B。
17. 由
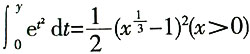
所确定的函数y=y(x)的极值为______。
A B C D
A
[解析] 在方程两边对x求导,得
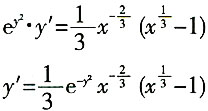
令y′=0(x>0),得驻点x=1。
当0<x<1时,y′<0,函数y(x)单调减少;当x>1时,y′>0,函数y(x)单调增加。
因此,y(x)在x=1处有极小值y(1),且
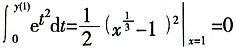
由此可得,极小值为y(1)=0,故选A。
18. 双曲线

在点p
0(x
0,y
0)处的切线及x=a(a为切线在x轴上的截距)所围图形的面积为A(右图中阴影部分),则以下选项中正确的是______。
- A.x0越大,面积A越大
- B.面积A与x0无关,恒为常数
- C.x0越大,面积A越小
- D.面积A不是x0的单调函数
A B C D
B
[解析] 切线斜率为
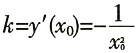
,所以切线方程为
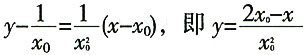
当y=0时,x=a=2x
0,所以有
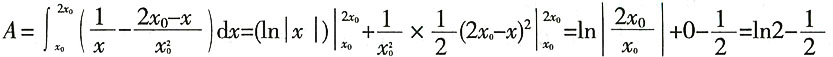
由以上论证,可得出B为正确答案。
20. 设

,则
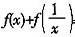
=______。
A.
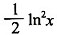
B.

C.ln
2x
D.
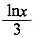
A B C D
A
[解析] 设
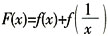
,由已知可得

故
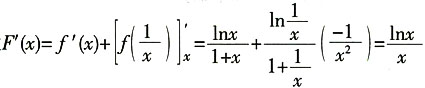
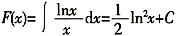
F(1)=f(1)+C=0,得C=0
故
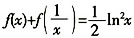
,A为正确答案。
21. 三阶行列式

的值为______。
A.(1+a
1)(1+a
2)(1+a
3)
B.
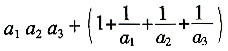
C.

D.以上均不正确
A B C D
B
[解析] 用拆项法计算三阶行列式D
3中每个元素为二数之和,共拆成8个行列式,其中不为0的行列式有4个,即
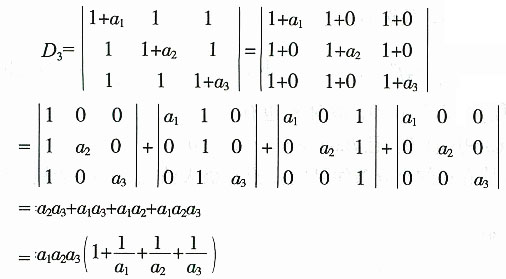
故B为正确答案。
22. 设A为n阶矩阵,A
*是A的伴随矩阵,若|A|=a≠0,则|2A
*|=______。
A.2a
n-1 B.2
na
n-1 C.2
na
n+1 D.

A B C D
B
[解析] 利用|rA|=|rnA|及|A*|=|A|n-1,可知B为正确答案。
24. 设x
1、x
2是非齐次线性方程组Ax=B的两个不同解,η
1、η
2是其导出组Ax=0的基础解系,c
1、c
2为任意常数,则方程组Ax=B的通解是______。
- A.(x1-x2)/2+c1η1+c2η2
- B.(x1+x2)/2+c1η1+c2(η1+η2)
- C.x1-x2+c1η1+c2(η1+η2)
- D.(x1-x2)/2+c1x1+c2(η1+η2)
A B C D
B
[解析] 因为(x1+x2)/2是Ax=B的一个解,η1,η2是导出组Ax=O的解,所以η1+η2也是Ax=0的解,易证η1,η1+η2线性无关,故η1,η1+η2也是Ax=0的一个基础解系,所以(x1+x2)/2+C1η1+C2(η1+η2)是方程组Ax=B的通解。
A、C、D中不含Ax=B的特解,故B为正确答案。
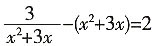 ,那么x2+3x的值为______。
,那么x2+3x的值为______。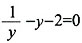 ,即y2+2y-3=0,解得y1=1,y2=-3,又因
,即y2+2y-3=0,解得y1=1,y2=-3,又因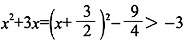 ,故舍去-3,x2+3x等于1,故正确答案为A。
,故舍去-3,x2+3x等于1,故正确答案为A。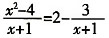 去分母并化简后得到的方程是______。
去分母并化简后得到的方程是______。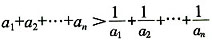 成立的n的取值范围为______。
成立的n的取值范围为______。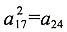 ,知(a1q16)2=a1q23。
,知(a1q16)2=a1q23。 ,故
,故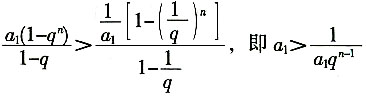
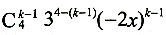 ,令xk-1=x2,得k=3,
,令xk-1=x2,得k=3,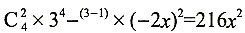 ,于是x2项的系数为216,故选D。
,于是x2项的系数为216,故选D。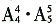
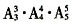
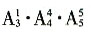
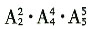
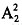 种排法,而油画内有
种排法,而油画内有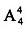 种排法,国画内有
种排法,国画内有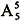 种排法,故共有
种排法,故共有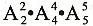 种排法,故选D。
种排法,故选D。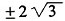
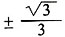
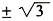
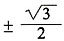
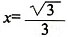 或
或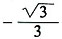 ,故选B。
,故选B。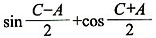 等于______。
等于______。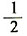
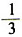
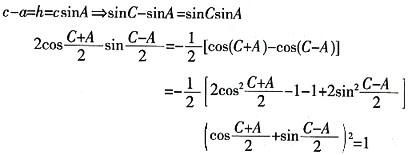
 ,选D。
,选D。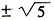
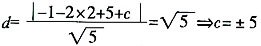 ,故选C。
,故选C。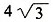 ,则焦点到AB的距离为______。
,则焦点到AB的距离为______。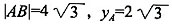 ,直线AB的方程为x=3,焦点(1,0)到AB的距离为2,故选C。
,直线AB的方程为x=3,焦点(1,0)到AB的距离为2,故选C。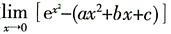 ,所以c=1。
,所以c=1。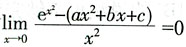
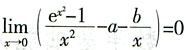

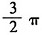
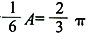 ,C为正确答案。
,C为正确答案。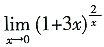 =______。
=______。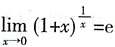 ,对函数
,对函数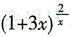 进行适当变形,利用公式
进行适当变形,利用公式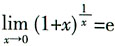 即可完成。
即可完成。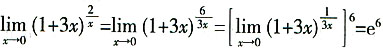
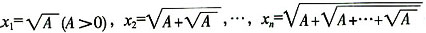 ,则
,则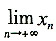 =______。
=______。
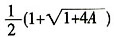
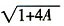
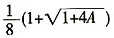
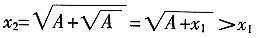 ,假设当n=k时,有xk>xk-1,那么由A+xk>A+xk-1,知
,假设当n=k时,有xk>xk-1,那么由A+xk>A+xk-1,知 ,即xk+1>xk,故对任意的n=k+1,有xn>xn-1成立,由数学归纳法知{xn}单调增加。
,即xk+1>xk,故对任意的n=k+1,有xn>xn-1成立,由数学归纳法知{xn}单调增加。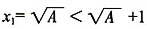 ,设当n=k时,有
,设当n=k时,有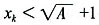 ,那么当n=k+1时,
,那么当n=k+1时,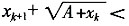
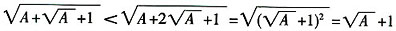 ,因此有上界,从而{xn}单调递增有上界,由单调有界定理知{Xn}收敛。
,因此有上界,从而{xn}单调递增有上界,由单调有界定理知{Xn}收敛。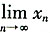
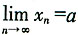 ,对
,对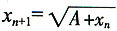 两端取极限,得
两端取极限,得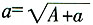 ,解得
,解得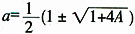 ,由(1)知a>0,因此
,由(1)知a>0,因此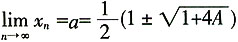 ,故选B。
,故选B。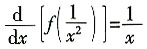 ,则
,则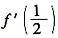 =______。
=______。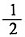
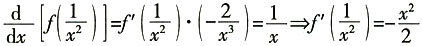 ,取
,取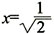 ,则
,则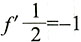 ,故选C。
,故选C。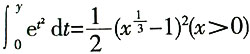 所确定的函数y=y(x)的极值为______。
所确定的函数y=y(x)的极值为______。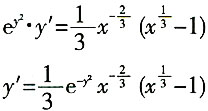
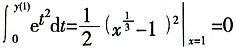
 在点p0(x0,y0)处的切线及x=a(a为切线在x轴上的截距)所围图形的面积为A(右图中阴影部分),则以下选项中正确的是______。
在点p0(x0,y0)处的切线及x=a(a为切线在x轴上的截距)所围图形的面积为A(右图中阴影部分),则以下选项中正确的是______。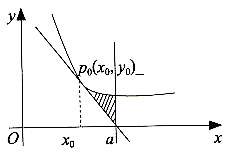
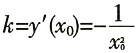 ,所以切线方程为
,所以切线方程为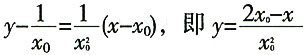
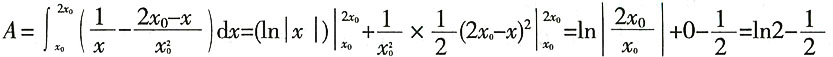
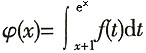 ,则φ″(0)=______。
,则φ″(0)=______。 ,则
,则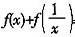 =______。
=______。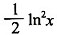

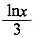
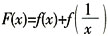 ,由已知可得
,由已知可得
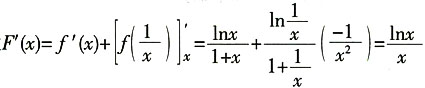
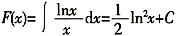
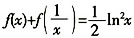 ,A为正确答案。
,A为正确答案。 的值为______。
的值为______。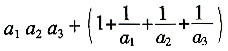

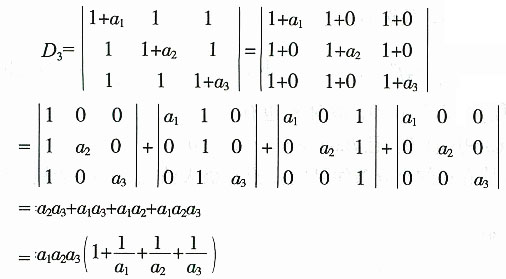

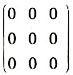
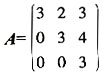 ,则An=______。
,则An=______。