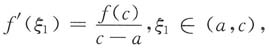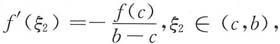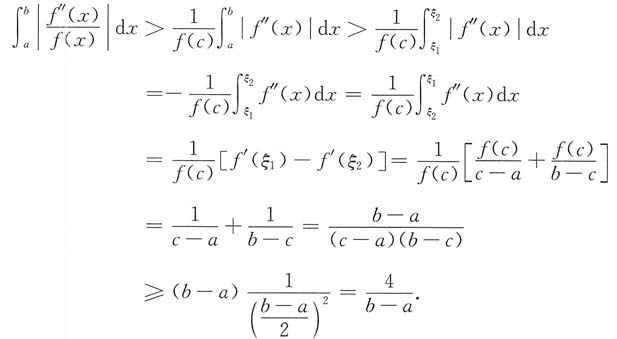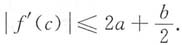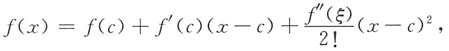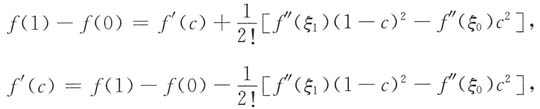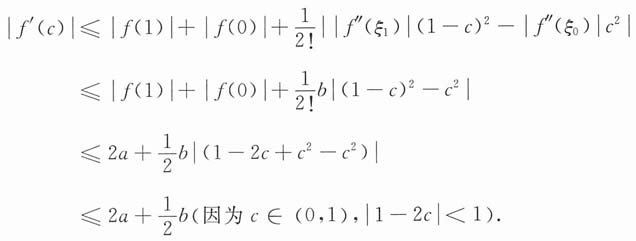一、选择题2. 对无穷级数
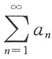
和
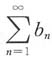
,下列命题成立的是______
A.
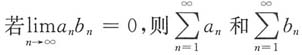
中至少一个收敛.
B.
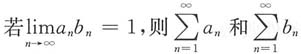
中至少一个发散.
C.若
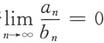
,则
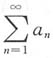
收敛时
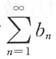
收敛.
D.若
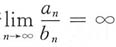
,则
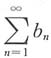
发散时
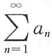
发散.
A B C D
B
[解析] 对选项A:取
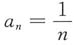
,b
n=1,则
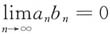
,但
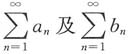
均发散,故排除A.
对选项C:取
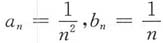
,则
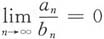
,且
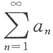
收敛,但
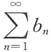
发散,故排除C.
对选项D:取
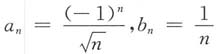
,则
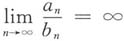
,且
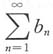
发散,但
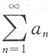
收敛.
故排除D.
对选项B:用反证法.若级数
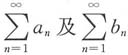
均收敛,则
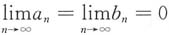
,从而
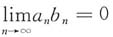
,与假设条件矛盾.因此,若
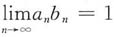
,则
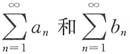
中至少一个发散,即选项B正确.
3. 设曲线L:f(x,y)=1(f(x,y)具有一阶连续偏导数),过第Ⅱ象限内的点M和第Ⅳ象限内的点N,Γ为L上从点M到点N的一段弧,则下列积分小于零的是______
A.
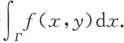
B.
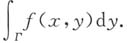
C.
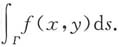
D.
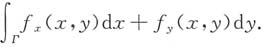
A B C D
B
[解析] 在Γ上f(x,y)=1,M在第Ⅱ象限,N在第Ⅳ象限,因此M点的纵坐标y
M大于N点的纵坐标y
N,因此
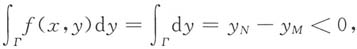
故应选B.
4. 在力场
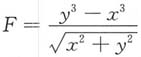
的作用下,一质点沿圆周x
2+y
2=1逆时针运动一周所作的功为______
A.
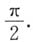
B.
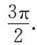
C.
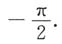
D.
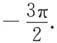
A B C D
D
[解析] 所求功为
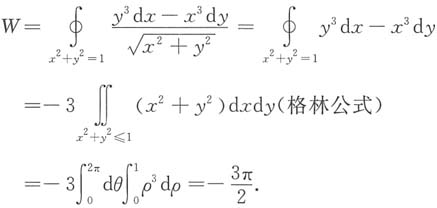
故选D.
5. 设
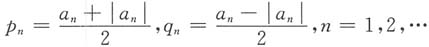
,则下列命题正确的是______
A.若
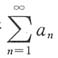
条件收敛,则
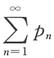
与
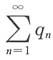
都收敛.
B.若
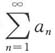
绝对收敛,则
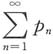
与
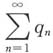
都收敛.
C.若
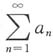
条件收敛,则
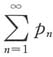
与
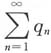
的敛散性都不定.
D.若
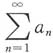
绝对收敛,则
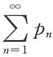
与
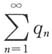
的敛散性都不定.
A B C D
B
[解析]
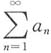
绝对收敛,即
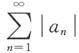
收敛,则级数
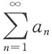
收敛,由收敛级数的运算性质,得级数
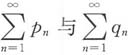
都收敛.故应选B.
6. 设u
n>0,n=1,2,…,若
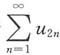
发散,
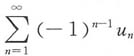
收敛,则下列结论正确的是______
A.
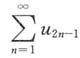
收敛,

发散.
B.
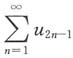
发散,
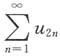
收敛.
C.

收敛.
D.

收敛.
A B C D
D
[解析] 由于
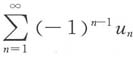
收敛,又
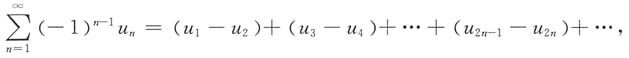
由性质收敛级数加括号不改变其收敛性知,级数

收敛,故应选D.
如令
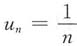
,显然
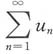
发散,
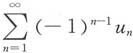
收敛.
但是级数
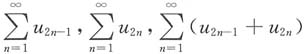
均发散,可排除A、B、C.
7. 设a
n>0(n=1,2,3,…),且
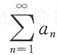
收敛,常数

,则级数
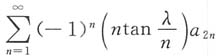
______
- A.绝对收敛.
- B.条件收敛.
- C.发散.
- D.敛散性与λ有关.
A B C D
A
[解析] 由于
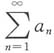
为正项级数且收敛,则级数
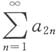
收敛,而
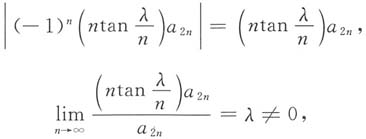
则

收敛,故
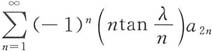
绝对收敛.
9. 设φ
1(x),φ
2(x),φ
3(x)为二阶非齐次线性方程y"+a
1(x)y'+a
2(x)y=f(x)的三个线性无关解,则该方程的通解为______
- A.C1[φ1(x)+φ2(x)]+C2φ3(x).
- B.C1[φ1(x)-φ2(x)]+C2φ3(x).
- C.C1[φ1(x)+φ2(x)]+C3[φ1(x)-φ3(x)].
- D.C1φ1(x)+C2φ2(x)+C3φ3(x),其中C1+C2+C3=1.
A B C D
D
[解析] 因为φ1(x),φ2(x),φ3(x)为方程y"+a1(x)y'+a2(x)y=f(x)的三个线性无关解,所以φ1(x)-φ3(x),φ2(x)-φ3(x),为方程y"+a1(x)y'+a2(x)y=0的两个线性无关解,于是方程y"+a1(x)y'+a2(x)y=f(x)的通解为
C1[φ1(x)-φ3(x)]+C2[φ2(x)-φ3(x)]+φ3(x),
即C1φ1(x)+C2φ2(x)+C3φ3(x),其中C3=1-C1-C2或C1+C2+C3=1,选D.
10. 设二阶常系数齐次线性微分方程y"+by'+y=0的每一个解y(x)都在区间(0,+∞)上有界,则实数b的取值范围是______
- A.[0,+∞).
- B.(-∞,0).
- C.(-∞,4].
- D.(-∞,+∞).
A B C D
A
[解析] 因为特征方程为λ
2+bλ+1=0,其判别式为Δ=b
2-4.
当b≠±2时,微分方程的通解为
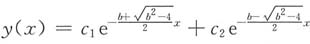
.所以
当b
2-4>0时,要使解y(x)在(0,+∞)上有界,只需要

,即b>2;
当b
2-4<0时,要使解y(x)在(0,+∞)上有界,只需要

的实部大于或等于零,即0≤b<2;
当b=2时,解y(x)=(c
1+c
2x)e
-x在区间(0,+∞)上有界;
当b=-2时,解y(x)=(c
1+c
2x)e
x在区间(0,+∞)上无界;
综上所述,当且仅当b≥0时,微分方程y"+by'+y=0的每一个解y(x)都在区间(0,+∞)上有界,故选A.
二、解答题1. 设f(x),g(x)在[a,b]上连续,在(a,b)内二阶可导,f(a)=f(b)=0,f'
+(a)f'
-(b)>0,且g(x)≠0(x∈[a,b]),g"(x)≠0(a<x<b),证明:存在ξ∈(a,b),使得
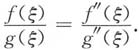
不失一般性,设f'
+(a)>0,f'
-(b)>0.
由f'
+(a)>0知,存在x
1∈(a,b),使得f(x
1)>f(a)=0;
由f'
-(b)>0知,存在x
2∈(a,b),使得f(x
2)<f(b)=0;
因为f(x
1)f(x
2)<0,所以由零点定理,存在c∈(a,b),使得f(c)=0.
令
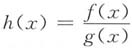
,显然h(x)在[a,b]上连续,有h(a)=h(c)=h(b)=0.
存在ξ
1∈(a,c),ξ
2∈(c,b),使得h'(ξ
1)=h'(ξ
2)=0.
而
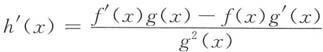
,所以
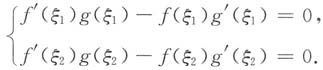
令φ(x)=f'(x)g(x)-f(x)g'(x),则φ(ξ
1)=φ(ξ
2)=0.
由罗尔定理,存在
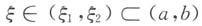
,使得φ'(ξ)=0,而
φ'(x)=f"(x)g(x)-f(x)g"(x),
所以
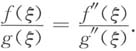
2. 证明:对0<x<a,存在0<θ<1,使得
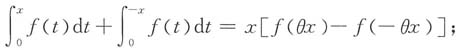
令
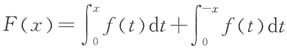
,显然F(x)在[0,x]上可导,且F(0)=0,由微分中值定理,存在0<θ<1,使得F(x)=F(x)-F(0)=F'(θx)x,即
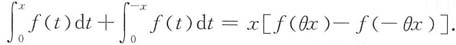
3. 求
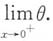
注意题设条件中有f'(0)=2,观察上式右边,要想出现f'(0)项,则须出现
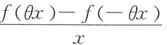
项,因此将上式两边同除以x
2并取极限,得
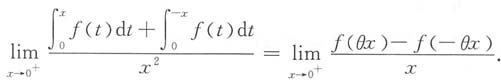
又
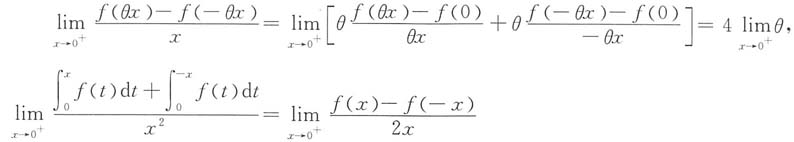
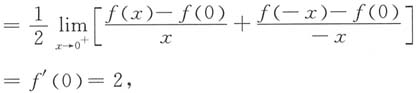
于是
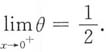
4. 设f(x)在[a,b]上连续,在(a,b)内可导,且f(a)=f(b)=1,试证存在两点ε,η∈(a,b),使得(e
2a+e
a+b+e
2b)[f(ξ)+f'(ξ)]=3e
3η-ξ.
对于这类问题的证明,关键是找对辅助函数.通常我们利用原函数法来求辅助函数,先对要证明的结果进行分析
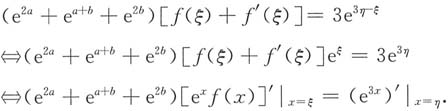
先对g(x)=e
3x用拉格朗日中值定理,再对F(x)=e
xf(x)用拉格朗日中值定理,然后乘以常数(e
2a+e
a+b+e
2b)可得待证的等式.
令g(x)=e
3x,则g(x)=e
3x在[a,b]上满足拉格朗日中值定理条件.
由拉格朗日中值定理,存在点η∈(a,b),使得
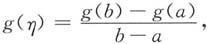
即
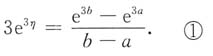
令F(x)=e
xf(x),由拉格朗日中值定理,存在点ξ∈(a,b),使得
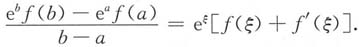
由f(b)=f(a)=1,可得
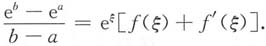
两边同时乘以(e
2a+e
a+b+e
2b),得
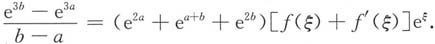
代入式①,可得(e
2a+e
a+b+e
2b)[f(ξ)+f'(ξ)]=3e
3η-ξ.
5. 设函数f(x)在[a,b]上连续,在(a,b)内可微,若a≥0,证明在(a,b)内存在三个数x
1,x
2,x
3,使
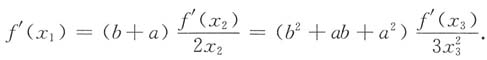
观察原等式可得
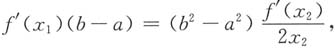
而由拉格朗日中值定理
f'(x
1)(b-a)=f(b)-f(a),
则有
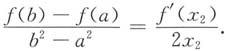
设g(x)=x
2,当a≥0时,f(x)和g(x)在[a,b]上满足柯西中值定理,故

使
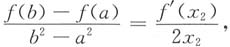
即

分析同上,对于右边等式,可设φ(x)=x
3,当a≥0时,f(x)和φ(x)在[a,b]上满足柯西定理的条件,故
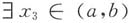
,使
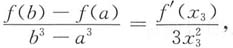
即
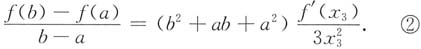
同样地,由拉格朗日中值定理知,必
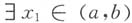
,使
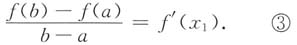
综合式①、②、③可得
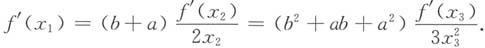
即得所证.
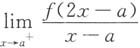 存在,证明:
存在,证明:6. 在(a,b)内,f(x)>0;
由x→a时,x-a→0,f'(x)在[a,b]上连续,及
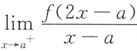
存在,且连续函数在某点的极限值等于该函数在此点的函数值.
故
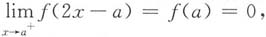
而f'(x)>0,所以f(x)在[a,b]上严格单调递增,故
f(x)>f(a)=0.
7.

解法一:使用柯西中值定理
令g(x)=x
2,
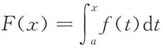
,则F'(x)=f(x),故在[a,b]上,g(x)与F(x)满足柯西定理的条件,存在ξ∈(a,b),使
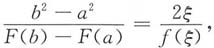
即得所证.
解法二:使用罗尔定理
令
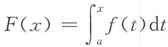
,设
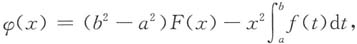
则φ(x)在[a,b]上连续,在(a,b)内可导,且
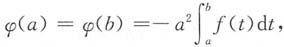
故φ(x)在[a,b]上满足罗尔定理条件,存在ξ∈(a,b),使
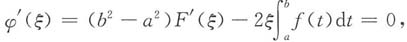
由F'(x)=f(x)及
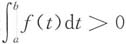
,即得所证.
8. 存在ξ≠η∈(a,b),使
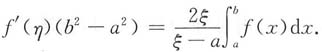
由第二小题中结论可知
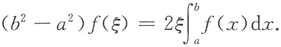
而f(a)=0,故在[a,ξ]上由拉格朗日中值定理知
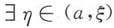
,使f(ξ)=f'(η)(ξ-a),
代入上式得
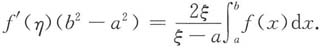
9. 设a
1,a
2,…,a
n为常数,且
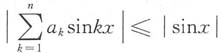
,
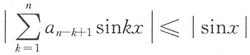
,试证明
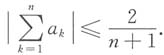
记
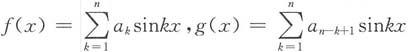
,显然,函数f(x)、g(x)连续,且
f(0)=g(0)=0,
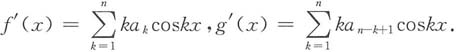
对任意一点x,函数f(x)与g(x)分别在[0,x]或[x,0]上应用拉格朗日中值定理有
f(x)-f(0)=f'(ξ
1)x,g(x)-g(0)=g'(ξ
2)x,
其中ξ
1,ξ
2在0与x之间,因此由题设条件得
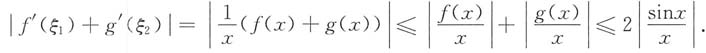
对上式两边令x→0,有ξ
1→0,ξ
2→0,使得
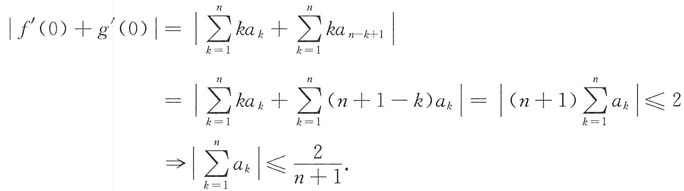
原结论成立.
10. 设函数f(x)在区间[a,b]上具有三阶连续导数,求证:存在ξ∈(a,b),使得
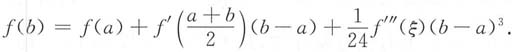
在带拉格朗日余项的泰勒公式
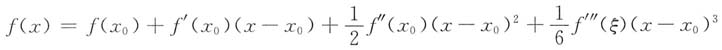
中分别取x=a与x=b,并取
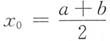
,可得
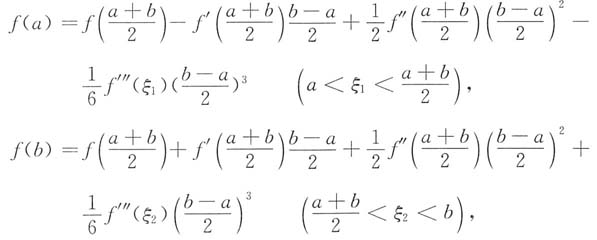
两式相减得
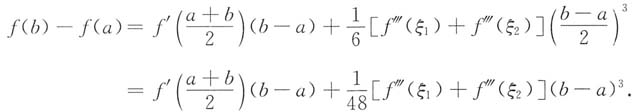
当f'"(ξ
1)=f'"(ξ
2)时取ξ=ξ
1(或ξ=ξ
2),否则由f'"(x)的连续性知存在ξ∈(ξ
1,ξ
2),
使得
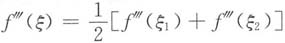
,代入上式即得存在
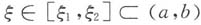
,使得
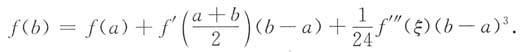
11. 已知a≤x≤b时,f'(x)>0,f"(x)>0,证明:
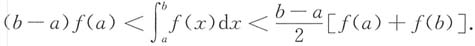
先证明左半边不等式.
由积分中值定理得
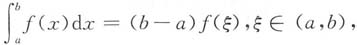
又因为f'(x)>0,所以f(ξ)>f(a).
所以
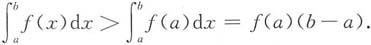
再证明右半边不等式.
可尝试构造函数并用单调性证明之.
设
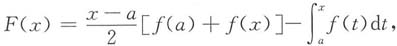
则
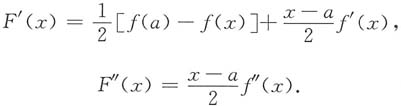
由f"(x)>0,知F"(x)>0,故F'(x)单调增加,F'(x)>F'(a)=0.
所以F(x)单调递增,F(b)>F(a)=0,即
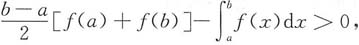
所以
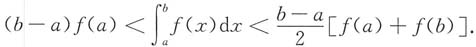
12. 已知f(x)在[a,b]上有连续的二阶导数,且f"(x)<0,f(a)=f(b)=0.试证:在(a,b)内f(x)>0,且
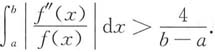
由f"(x)<0司知,f(x)在[a,b]上是凸函数,由凸函数性质知,f(x)在(a,b)内的图形位于(a,f(a))和(b,f(b))之间的线段之上,即x轴之上,所以在(a,b)内f(x)>0.
由上可知,存在一点c∈(a,b),使得
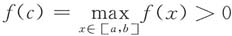
,由拉格朗日中值定理得
f(c)-f(a)=f'(ξ
1)(c-a),即
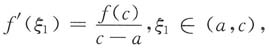
f(b)-f(c)=f'(ξ
2)(b-c),即
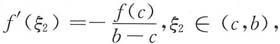
则
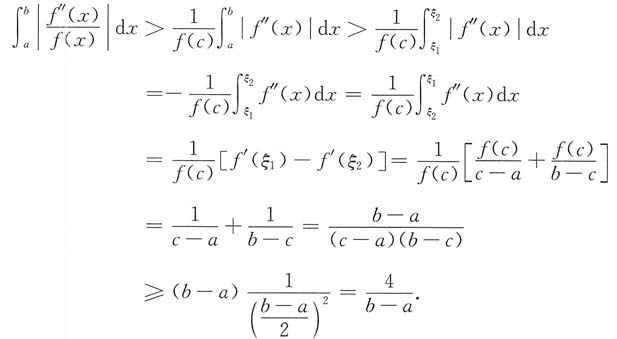
13. 设f(x)在[0,1]上具有二阶导数,且满足条件|f(x)|≤a,|f"(x)|≤b,其中a,b都是非负常数,c是(0,1)内任意一点,证明:
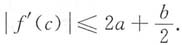
由于问题中涉及f(x)与其导致、二阶导数的关系,可考虑用勒公式证明之.f(x)在c处的泰勒展开式为
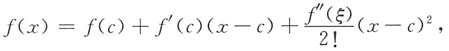
其中ξ在c与x之间.
取x=0,1得

两式相减得
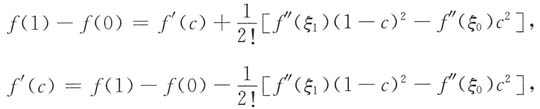
由此
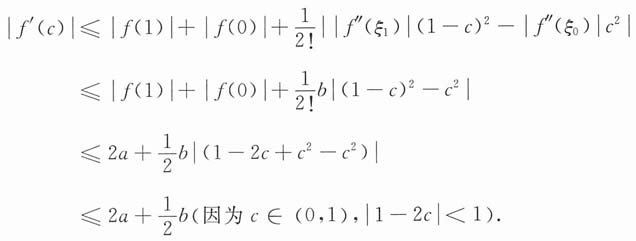
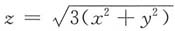 与
与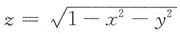 围成的空间区域,三重积分
围成的空间区域,三重积分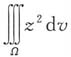 在球坐标系下化为累次积分是______
在球坐标系下化为累次积分是______
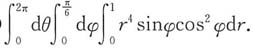
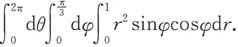
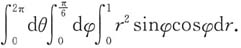
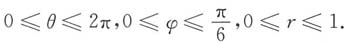
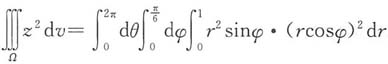
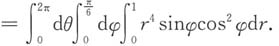
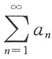 和
和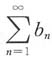 ,下列命题成立的是______
,下列命题成立的是______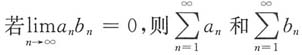 中至少一个收敛.
中至少一个收敛.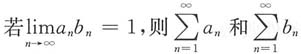 中至少一个发散.
中至少一个发散.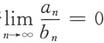 ,则
,则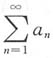 收敛时
收敛时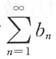 收敛.
收敛.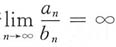 ,则
,则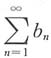 发散时
发散时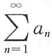 发散.
发散.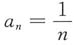 ,bn=1,则
,bn=1,则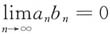 ,但
,但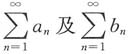 均发散,故排除A.
均发散,故排除A.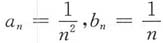 ,则
,则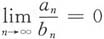 ,且
,且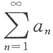 收敛,但
收敛,但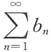 发散,故排除C.
发散,故排除C.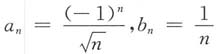 ,则
,则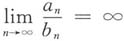 ,且
,且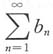 发散,但
发散,但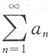 收敛.
收敛.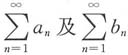 均收敛,则
均收敛,则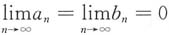 ,从而
,从而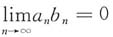 ,与假设条件矛盾.因此,若
,与假设条件矛盾.因此,若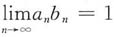 ,则
,则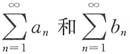 中至少一个发散,即选项B正确.
中至少一个发散,即选项B正确.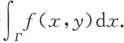
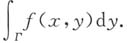
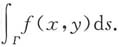
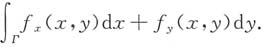
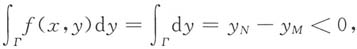
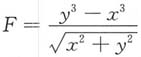 的作用下,一质点沿圆周x2+y2=1逆时针运动一周所作的功为______
的作用下,一质点沿圆周x2+y2=1逆时针运动一周所作的功为______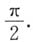
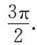
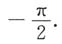
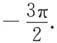
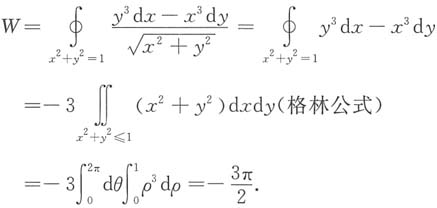
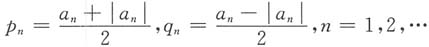 ,则下列命题正确的是______
,则下列命题正确的是______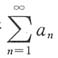 条件收敛,则
条件收敛,则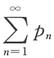 与
与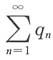 都收敛.
都收敛.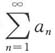 绝对收敛,则
绝对收敛,则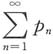 与
与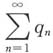 都收敛.
都收敛.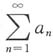 条件收敛,则
条件收敛,则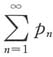 与
与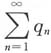 的敛散性都不定.
的敛散性都不定.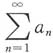 绝对收敛,则
绝对收敛,则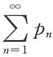 与
与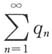 的敛散性都不定.
的敛散性都不定.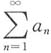 绝对收敛,即
绝对收敛,即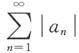 收敛,则级数
收敛,则级数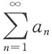 收敛,由收敛级数的运算性质,得级数
收敛,由收敛级数的运算性质,得级数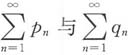 都收敛.故应选B.
都收敛.故应选B.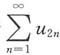 发散,
发散,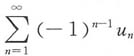 收敛,则下列结论正确的是______
收敛,则下列结论正确的是______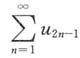 收敛,
收敛, 发散.
发散.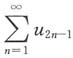 发散,
发散,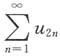 收敛.
收敛. 收敛.
收敛. 收敛.
收敛.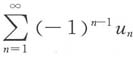 收敛,又
收敛,又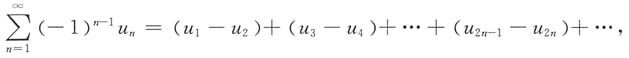 由性质收敛级数加括号不改变其收敛性知,级数
由性质收敛级数加括号不改变其收敛性知,级数 收敛,故应选D.
收敛,故应选D.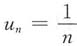 ,显然
,显然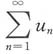 发散,
发散,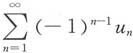 收敛.
收敛.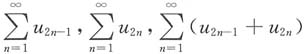 均发散,可排除A、B、C.
均发散,可排除A、B、C.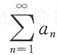 收敛,常数
收敛,常数 ,则级数
,则级数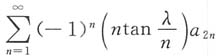 ______
______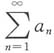 为正项级数且收敛,则级数
为正项级数且收敛,则级数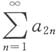 收敛,而
收敛,而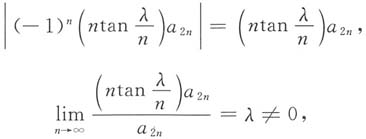
 收敛,故
收敛,故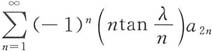 绝对收敛.
绝对收敛. ,级数
,级数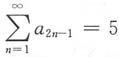 ,则级数
,则级数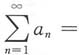 ______
______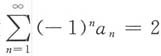 ,级数
,级数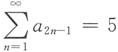 ,则级数
,则级数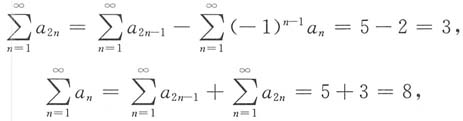
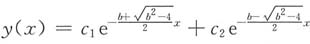 .所以
.所以 ,即b>2;
,即b>2; 的实部大于或等于零,即0≤b<2;
的实部大于或等于零,即0≤b<2;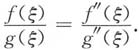
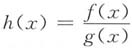 ,显然h(x)在[a,b]上连续,有h(a)=h(c)=h(b)=0.
,显然h(x)在[a,b]上连续,有h(a)=h(c)=h(b)=0.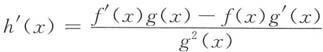 ,所以
,所以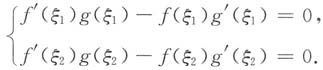
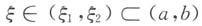 ,使得φ'(ξ)=0,而
,使得φ'(ξ)=0,而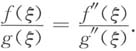
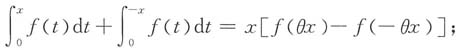
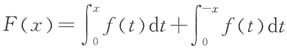 ,显然F(x)在[0,x]上可导,且F(0)=0,由微分中值定理,存在0<θ<1,使得F(x)=F(x)-F(0)=F'(θx)x,即
,显然F(x)在[0,x]上可导,且F(0)=0,由微分中值定理,存在0<θ<1,使得F(x)=F(x)-F(0)=F'(θx)x,即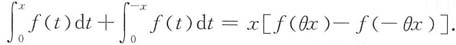
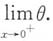
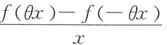 项,因此将上式两边同除以x2并取极限,得
项,因此将上式两边同除以x2并取极限,得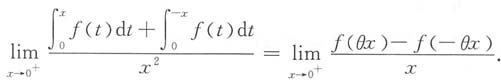
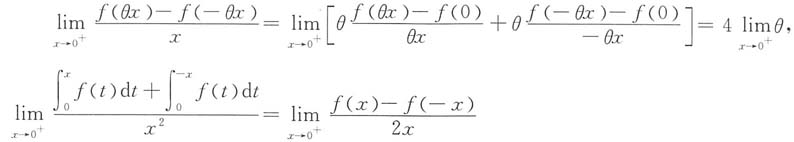
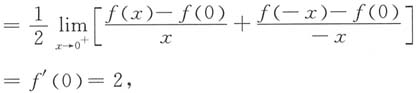
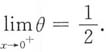
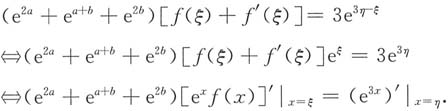
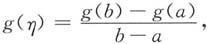
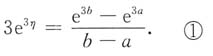
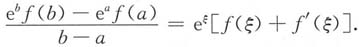
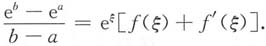
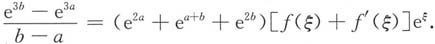
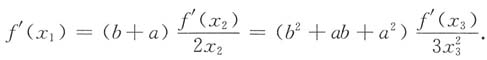
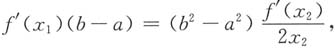
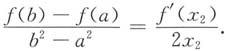

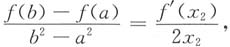

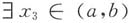 ,使
,使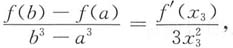
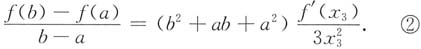
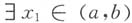 ,使
,使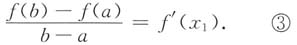
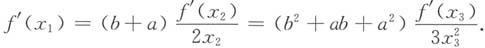
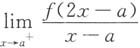 存在,证明:
存在,证明: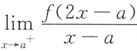 存在,且连续函数在某点的极限值等于该函数在此点的函数值.
存在,且连续函数在某点的极限值等于该函数在此点的函数值.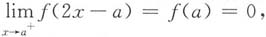

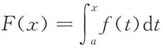 ,则F'(x)=f(x),故在[a,b]上,g(x)与F(x)满足柯西定理的条件,存在ξ∈(a,b),使
,则F'(x)=f(x),故在[a,b]上,g(x)与F(x)满足柯西定理的条件,存在ξ∈(a,b),使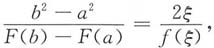
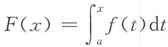 ,设
,设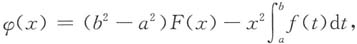
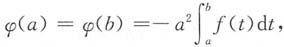
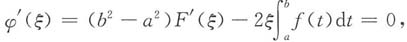
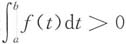 ,即得所证.
,即得所证.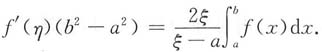
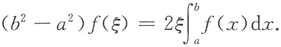
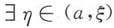 ,使f(ξ)=f'(η)(ξ-a),
,使f(ξ)=f'(η)(ξ-a),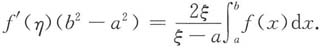
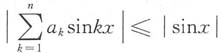 ,
,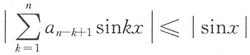 ,试证明
,试证明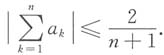
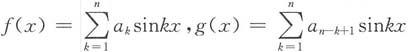 ,显然,函数f(x)、g(x)连续,且
,显然,函数f(x)、g(x)连续,且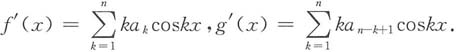
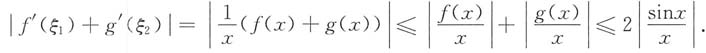
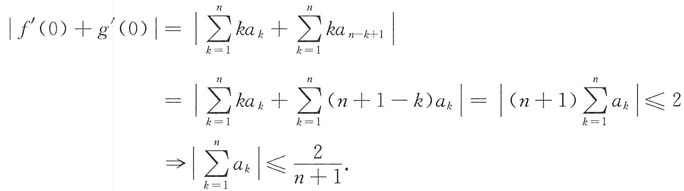
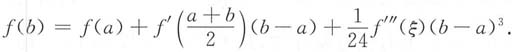
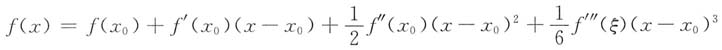
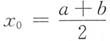 ,可得
,可得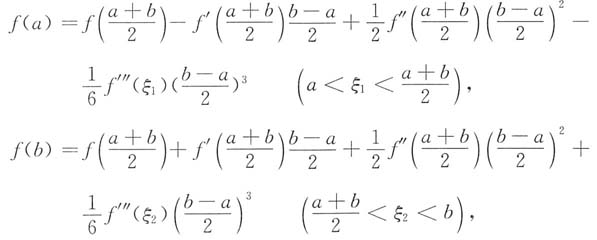
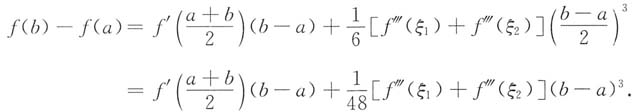
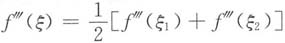 ,代入上式即得存在
,代入上式即得存在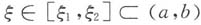 ,使得
,使得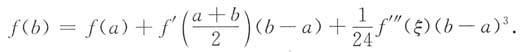
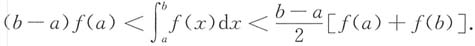
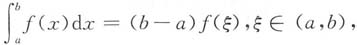
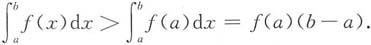
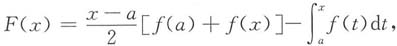
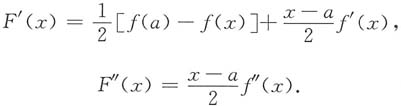
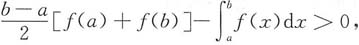
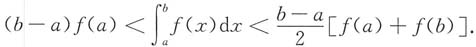
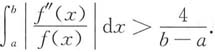
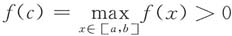 ,由拉格朗日中值定理得
,由拉格朗日中值定理得