一、选择题2. 设X~P(λ),P
1,P
2分别为随机变量X取偶数和奇数的概率,则______
- A.P1=P2.
- B.P1<P2.
- C.P1>P2.
- D.P1,P2大小关系不定.
A B C D
C
[解析] 若X~P(λ),则
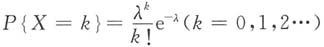
,其中X取偶数的概率为
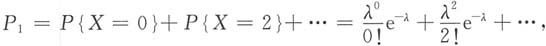
X取奇数的概率为

于是
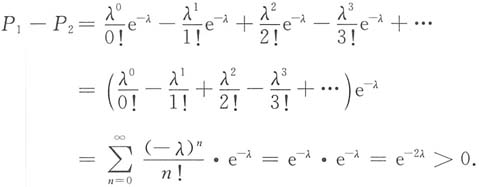
应选C.
3. 设随机变量X的密度函数为f(x),且f(-x)=f(x),F(x)是X的分布函数,则对于任意实数a,有______
A.
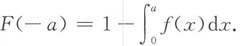
B.
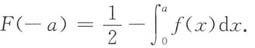
C.F(-a)=F(a).
D.F(-a)=2F(a)-1.
A B C D
B
[解析] 概率密度f(x)为偶函数,于是对于任意实数a,有F(-a)=1-F(a)成立;利用区间可加性得
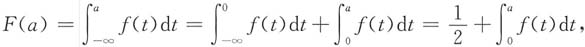
结合上面的等式,于是得
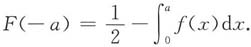
应选B.
4. 设二维随机变量(X,Y)在区域D:x
2+y
2≤9a
2(a>0)上服从均匀分布,p=P{X
2+9Y
2≤9a
2},则
A.p的值与a无关,且
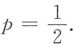
B.p的值与a无关,且
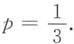
C.p的值随a值的增大而增大.
D.p的值随a值的增大而减小.
A B C D
B
[解析] 因为(X,Y)在区域D:x
2+y
2≤9a
2上服从均匀分布,
所以(X,Y)的联合密度函数为
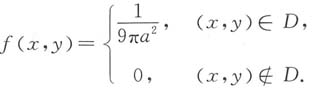
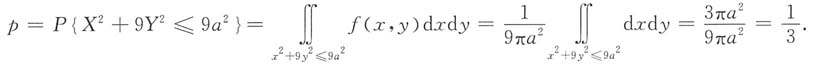
故选B.
6. 已知总体X的期望E(X)=0,方差D(X)=σ
2.X
1,…,X
n是来自总体X的简单随机样本,其均值为
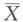
,则下面可以作为σ
2无偏估计量的是______
A.
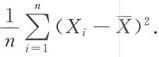
B.
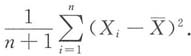
C.
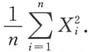
D.
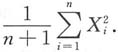
A B C D
C
[解析] 由于E(X)=0,D(X)=E(X
2)=σ
2,则

所以选择C.对于A,B选项,由E(S
2)=σ
2,知
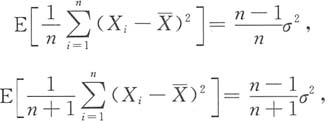
均不是σ
2的无偏估计量.
8. 设X
1,X
2,…,X
n是来自总体X的简单随机样本,
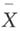
是样本均值,C为任意常数,则______
A.
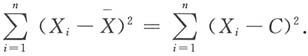
B.

C.
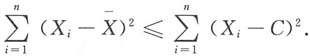
D.
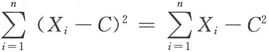
A B C D
C
[解析]
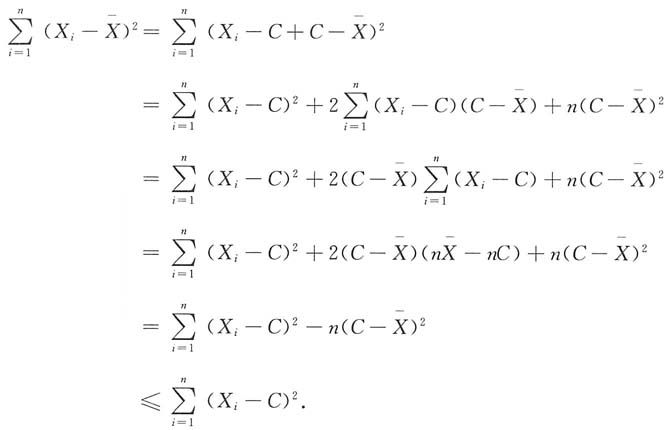
故选C.
9. 设总体X服从正态分布N(0,σ
2),X
1,X
2,…,X
10是来自X的简单随机样本,统计量
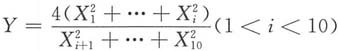
服从F分布,则i等于______
A B C D
B
[解析] 因为X
1,X
2,…,X
10是来自X的简单随机样本,故独立同分布于N(0,σ
2)
因此
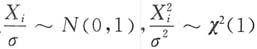
,则有

又
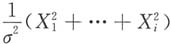
与
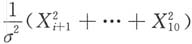
相互独立,故
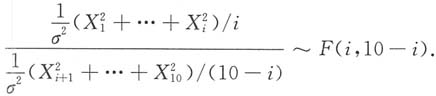
与Y比较,得
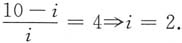
故选B.
二、解答题1. 每次从1,2,3,4,5中任取一个数,且取后放回,用b
i表示第i次取出的数(i=1,2,3),三维列向量b=(b
1,b
2,b
3)
T,三阶方阵

,求线性方程组Ax=b有解的概率.
对增广矩阵
作初等行变换有
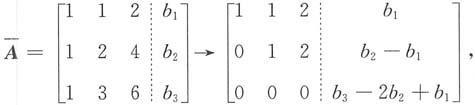
于是Ax=b有解的充要条件是
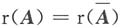
,即b
3-2b
2+b
1=0,其中b
1,b
2,b
3相互独立,且分布律相同:
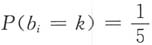
,k=1,2,3,4,5,i=1,2,3.
所以Ax=b有解的概率为
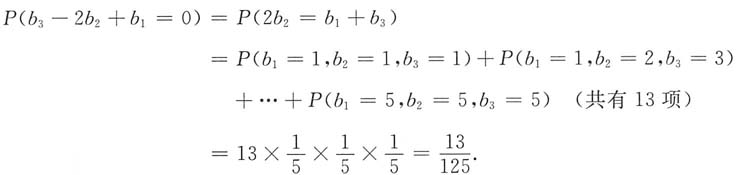
求:2. 甲、乙投球次数X
1与X
2的分布;
每次投篮是相互独立的与其他几次无关.
事件X1=n表示“甲投了n次”,即“甲、乙各自在前n-1次没有投进,在第n次时甲投进或乙投进”,所以
P{X1-n}=(q1q2)n-1(p1+q1p2),n=1,2,…其中:qi=1-pi,i=1,2.
事件“X2=m”表示“乙投了m次”,即“甲、乙前m-1次均没有投进,甲在第m次也没有投进,乙在第m次投进”,或“甲、乙前m次均没有投进,甲在第m+1次投进”.
特殊地,当m=0时,表示甲第一次就投中,所以
P{X2=m}=(q1q2)m-1(q1p2+q1q2p1)=q1(p2+q2p1)(q1q2)m-1,m=1,2,…
3. 若使甲、乙两人赢得比赛的概率相同,则p
1,p
2满足什么条件?
设事件A表示“甲获胜”,则总投篮次数为奇数.当X
1+X
2=2n-1时,意味着甲、乙前n-1次都未投进,甲在第n次投进,于是有P{X
1+X
2=2n-1}=p
1(q
1q
2)
n-1,则
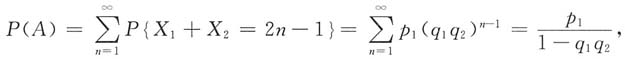
若甲、乙两人赢得比赛的概率相同,则
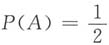
,可得
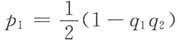
,即
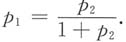
4. 设随机变量X在区间(0,1)上服从均匀分布,又
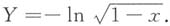
求Y的概率密度f
Y(y)与分布函数F
Y(y).
解法一:应用单调函数公式法先求Y的概率密度f
Y(y).
由于X在(0,1)内取值
所以
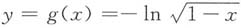
的值域为(0,+∞),且y=g(x)在(0,1)单调.
因此其反函数
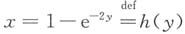
在(0,+∞)内单调可导,其导数h'(y)=2e
-2y,在其定义域(0,+∞)内恒不为零.
又因为X的概率密度
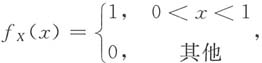
所以Y的概率密度
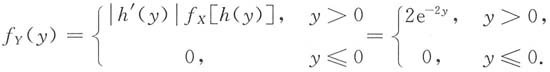
因此可见Y服从参数为2的指数分布,其分布函数为
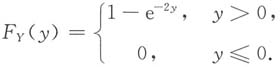 解法二:
解法二:用分布函数法先求出Y的分布函数F
Y(y).
当y≤0时,F
Y(y)=0;
当y>0时,0<x=1-e
-2y<1,
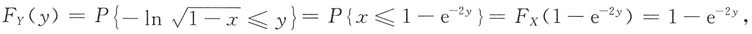
最后一步是由于X服从(0,1)上的均匀分布.
故所求Y的分布函数为
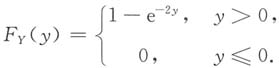
将F
Y(y)对y求导,得
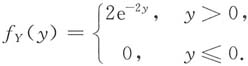
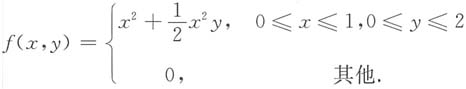
试求:5. (X,Y)的分布函数;
①当x≤0或y≤0时,f(x,y)=0,故F(x,y)=0.
②当0<x≤1,0<y≤2时,
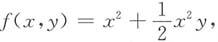
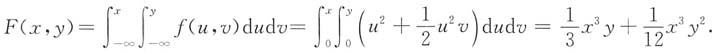
③当0<x≤1,y>2时,
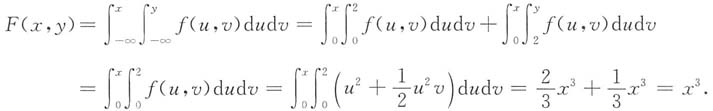
④当x>1,0<Y≤2时,
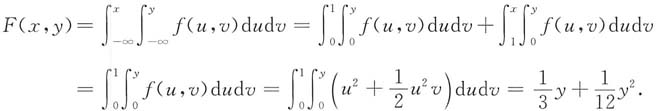
⑤当x>1,y>2时,
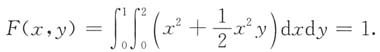
综上所述,分布函数为
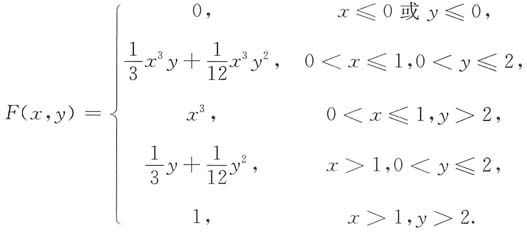
6. (X,Y)的边缘分布密度;
当0≤x≤1时,
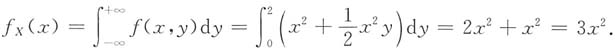
当0≤y≤2时,
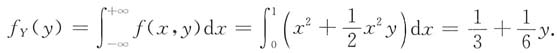
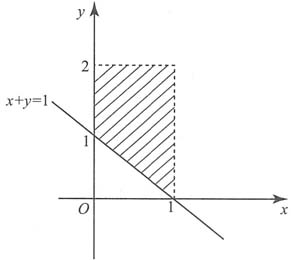
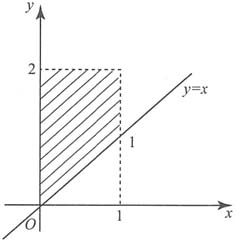
7. 概率P{X+Y>1},P{Y>X}及
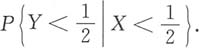
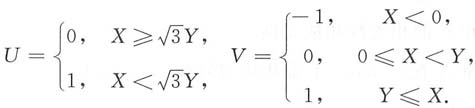
8. 求(U,V)的联合分布律;
由题设可知
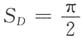
,故
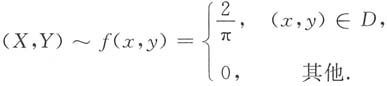
(U,V)的可能值为(0,0),(0,-1),(0,1),(1,-1),(1,0),(1,1).
则
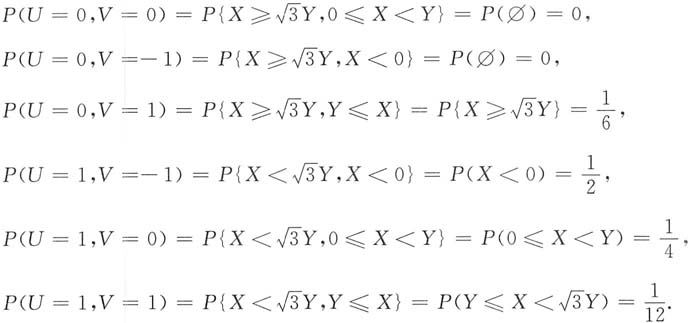
(U.V)的联合分布律为

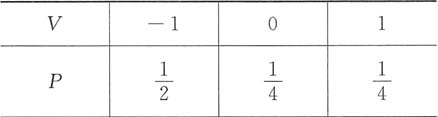
9. 求关于V的边缘分布律;
由(U,V)的联合分布律得V的边缘分布律为
11. 设随机变量X的概率密度为
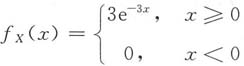
,求随机变量
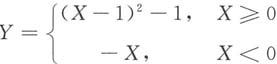
的分布函数F
Y(y).
记
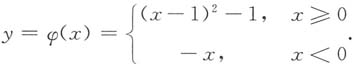
如下图所示,φ(x)在[0,+∞)内最小值为-1,无最大值,在[0,+∞)左端点处的值为0.y=-1,0将y轴分成(-∞,-1),[-1,0),[0,+∞)三个区间.
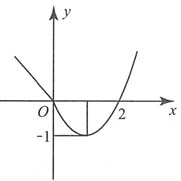
当y∈(-∞,-1)时,F
Y(y)=0.
当y∈[-1,0)时,纵坐标为y的水平直线关于曲线y=φ(x)内的集合在x轴上的投影与[0,+∞)的交集为
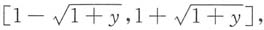
F
Y(y)=f
X(x)在
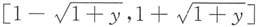
上的积分为
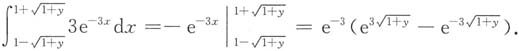
当y∈[0,+∞)时,纵坐标为y的水平直线关于曲线y=φ(x)内的集合在x轴的投影与[0,+∞)的交集为
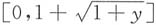
,此时
F
Y(y)=f
X(x)在
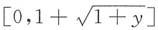
上的积分为
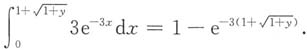
综上所述,y的分布函数为
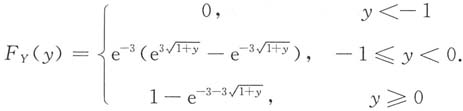
12. 求(X,Y)的联合概率密度,并问X与Y是否独立;
根据题设X在(0,2)上服从均匀分布,其密度函数为
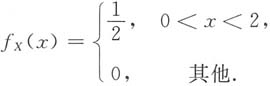
而变量Y,在X=x(1<-x<2)的条件下,在区间(1,x)上服从均匀分布,所以其条件概率密度为
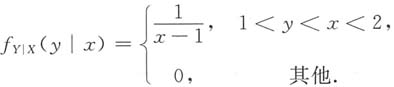
再根据条件概率密度的定义,可得联合概率密度
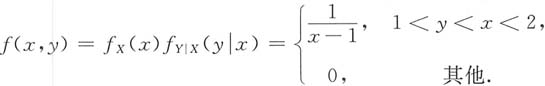
又
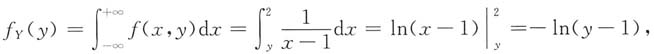
所以
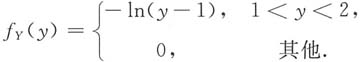
由于f
X(x)f
Y(y)≠f(x,y),所以X与Y不独立.
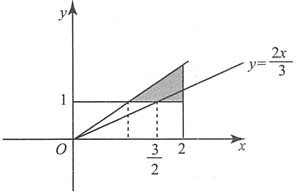
13. 求P{3Y≤2X};
如下图所示,
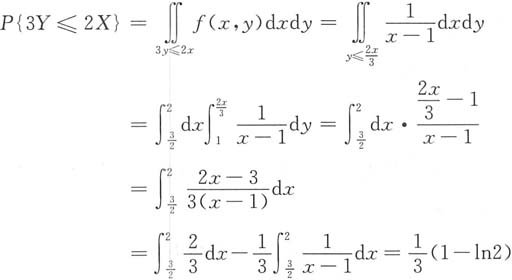
14. 记Z=X-Y,求Z的概率密度f
Z(z).
已知(x,y)~f(x,y),则Z=X-Y的取值范围为0<Z<1.当0<z<1时,Z=X-Y的分布函数为
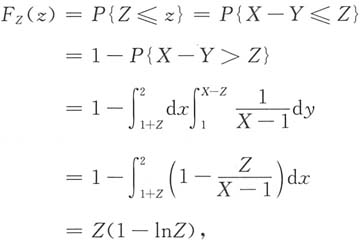
则
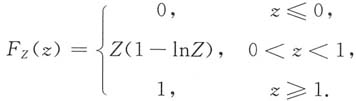
故
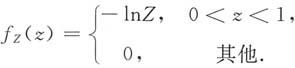
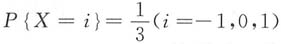 ,Y的概率密度函数为
,Y的概率密度函数为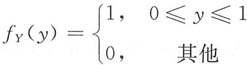 ,设Z=X+Y.
,设Z=X+Y.
求:15.
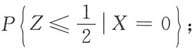
16. Z的概率密度函数.
F
Z(z)=P{Z≤z}=P{X+Y≤z}=P{X=-1,Y≤z+1}+P{X=0,Y≤z}+P{X=1,Y≤z-1}.因为X与Y相互独立,故
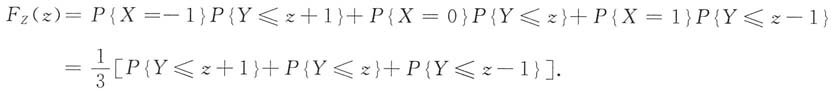
①当z+1<0(z-1<-2),即z<-1时,f
Y(y)=0,从而F
Z(z)=0;
②当0≤z+1<1(-2≤z-1<-1),即-1≤z<0时,
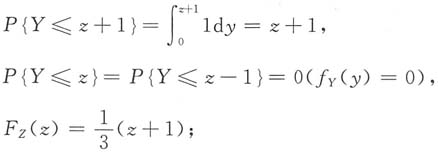
③当-1≤z-1<0(1≤z+1<2),即0≤z<1时,

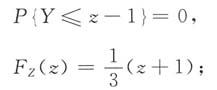
④当0≤z-1<1(2≤z+1<3),即1≤z<2时,
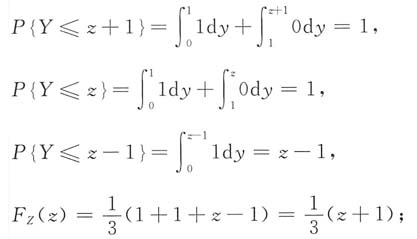
⑤当1≤z-1(3≤z+1),即z≥2时,
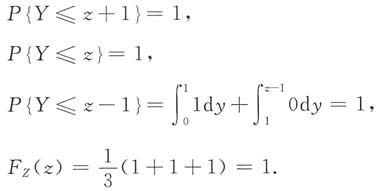
综上

故
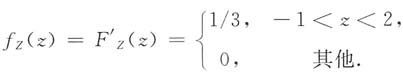
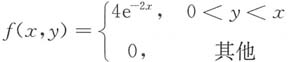 ,令随机变量U=X+Y,V=X-Y.
,令随机变量U=X+Y,V=X-Y.
求:17. U的分布函数F
1(u);
当u<0时,F
1(u)=0;
当u≥0时,
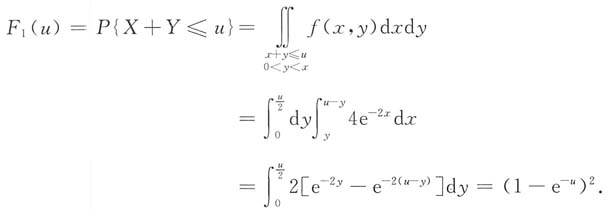
故U的分布函数F
1(u)为
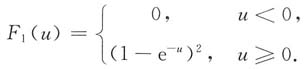
18. V的分布函数F
2(v);
当v<0时,F
2(v)=0;
当v≥0时,

故V的分布函数F
2(v)为
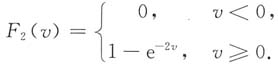
19. P{U≤u,V≥v}(u>v>0),并判断U与V是否独立.
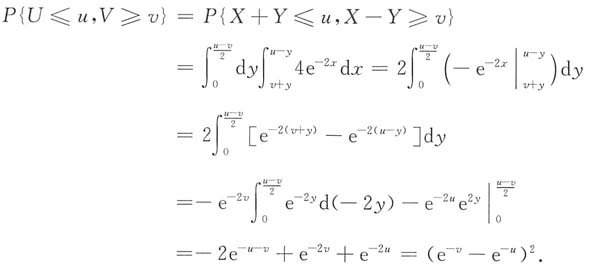
当u>0,v>0时,P{U≤u}P{V≥v}=F
1(u)·[1-F
2(v)]=e
-2v(1-e
-u)
2≠P{U≤u,V≥v},从而可知,U与V不独立.
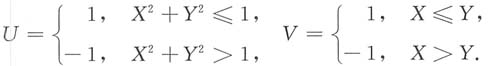
求:20. U和V的联合概率分布;
(U,V)的可能取值为(-1,-1),(-1,1),(1,-1,),(1,1),如下图.
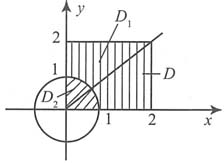
依题意知,X与Y的联合概率密度为
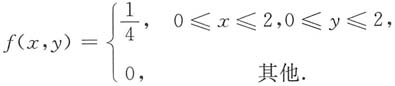
则有
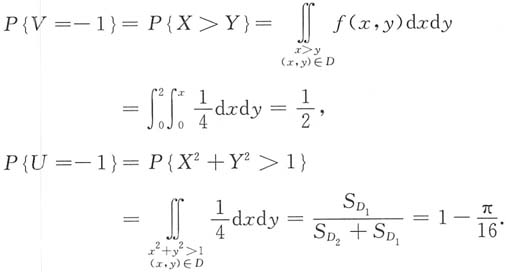
同理
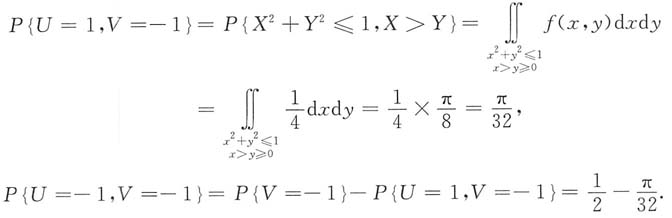
类似地可以计算出其他P
ij的值:
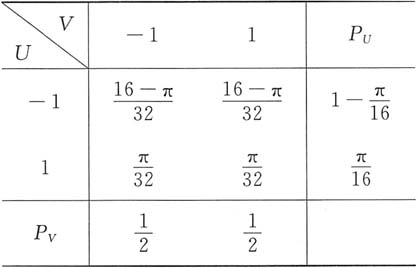
21. 讨论U和V的相关性和独立性.
从(U,V)的联合分布与边缘分布可以计算出

所以E(UV)=E(U)·E(V),U与V不相关;又因为P{U=u,V=v}=P{U=u}·P{V=v},所以U与V相互独立.
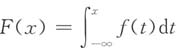 ,由此可知正确答案是B.
,由此可知正确答案是B.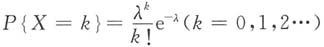 ,其中X取偶数的概率为
,其中X取偶数的概率为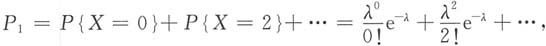

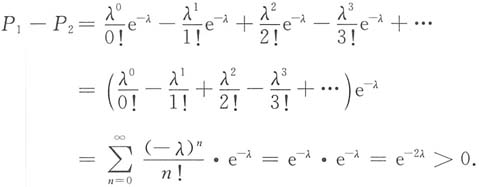
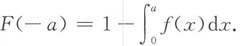
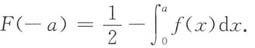
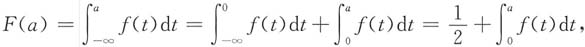 结合上面的等式,于是得
结合上面的等式,于是得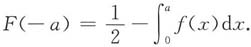 应选B.
应选B.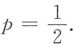
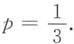
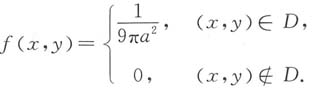
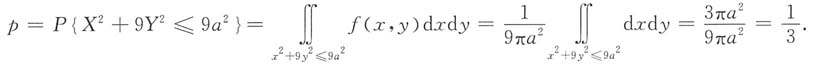

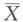 ,则下面可以作为σ2无偏估计量的是______
,则下面可以作为σ2无偏估计量的是______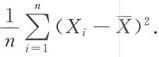
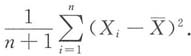
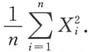
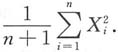

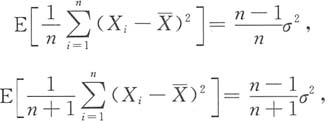
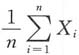 依概率收敛于其数学期望,只要{Xn,n≥1}满足______
依概率收敛于其数学期望,只要{Xn,n≥1}满足______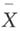 是样本均值,C为任意常数,则______
是样本均值,C为任意常数,则______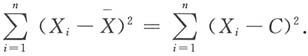

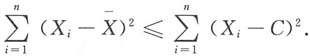
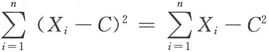
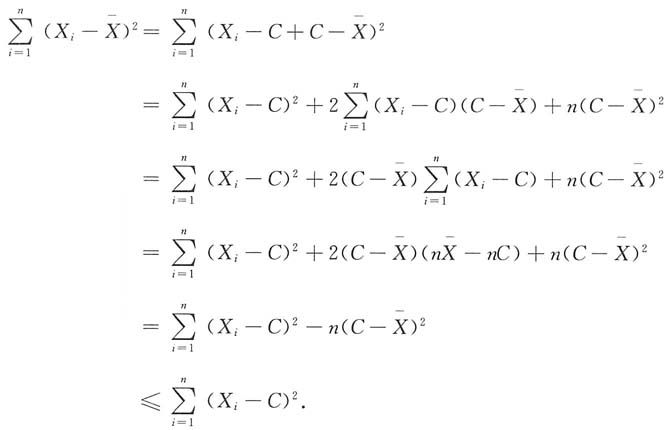
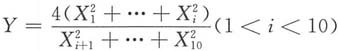 服从F分布,则i等于______
服从F分布,则i等于______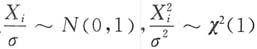 ,则有
,则有 又
又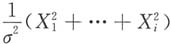 与
与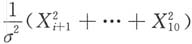 相互独立,故
相互独立,故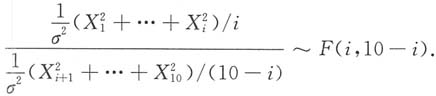 与Y比较,得
与Y比较,得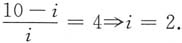
 ,求线性方程组Ax=b有解的概率.
,求线性方程组Ax=b有解的概率.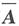 作初等行变换有
作初等行变换有
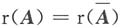 ,即b3-2b2+b1=0,其中b1,b2,b3相互独立,且分布律相同:
,即b3-2b2+b1=0,其中b1,b2,b3相互独立,且分布律相同: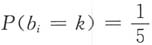 ,k=1,2,3,4,5,i=1,2,3.
,k=1,2,3,4,5,i=1,2,3.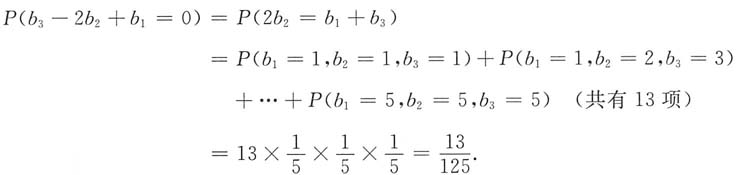
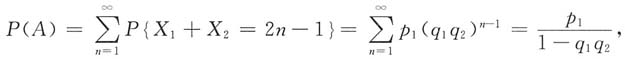
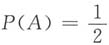 ,可得
,可得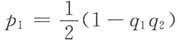 ,即
,即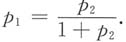
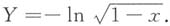
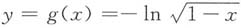 的值域为(0,+∞),且y=g(x)在(0,1)单调.
的值域为(0,+∞),且y=g(x)在(0,1)单调.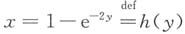 在(0,+∞)内单调可导,其导数h'(y)=2e-2y,在其定义域(0,+∞)内恒不为零.
在(0,+∞)内单调可导,其导数h'(y)=2e-2y,在其定义域(0,+∞)内恒不为零.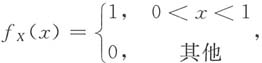 所以Y的概率密度
所以Y的概率密度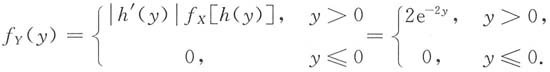 因此可见Y服从参数为2的指数分布,其分布函数为
因此可见Y服从参数为2的指数分布,其分布函数为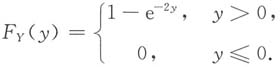
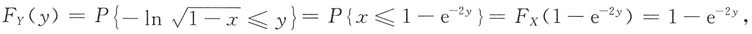 最后一步是由于X服从(0,1)上的均匀分布.
最后一步是由于X服从(0,1)上的均匀分布.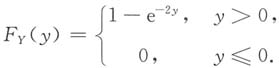 将FY(y)对y求导,得
将FY(y)对y求导,得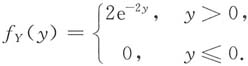
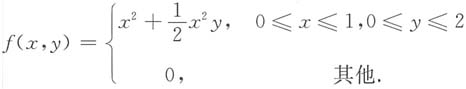
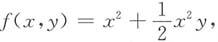
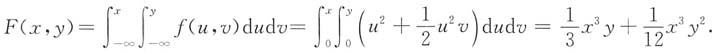
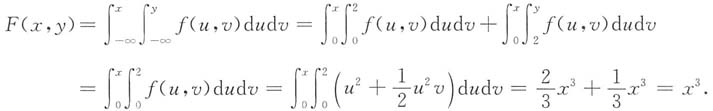
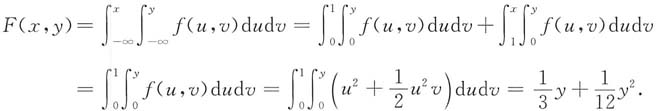
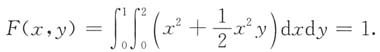
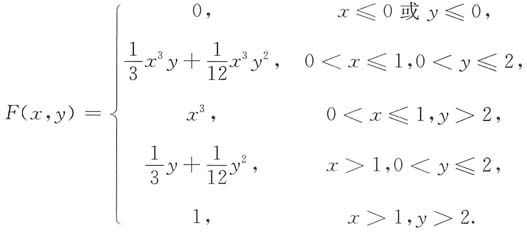
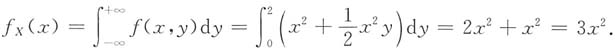
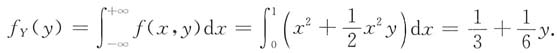
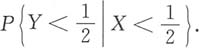
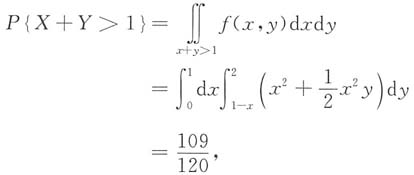
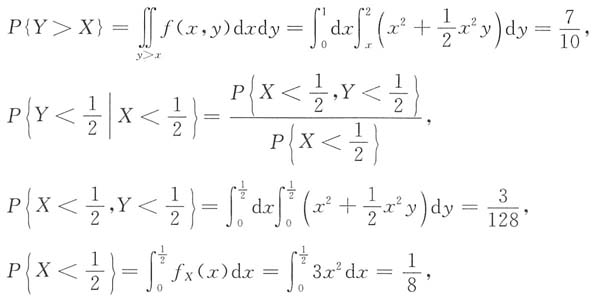
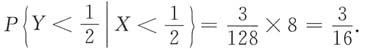
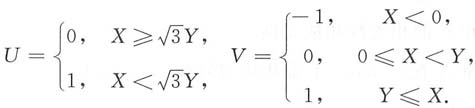
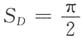 ,故
,故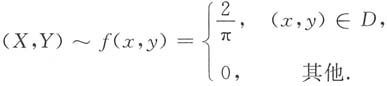 (U,V)的可能值为(0,0),(0,-1),(0,1),(1,-1),(1,0),(1,1).
(U,V)的可能值为(0,0),(0,-1),(0,1),(1,-1),(1,0),(1,1).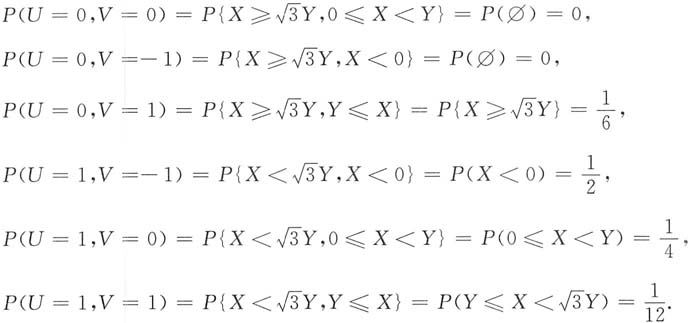 (U.V)的联合分布律为
(U.V)的联合分布律为

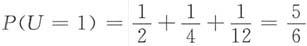 ,所以
,所以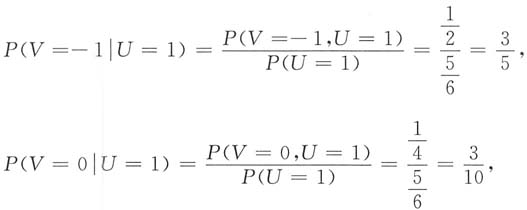
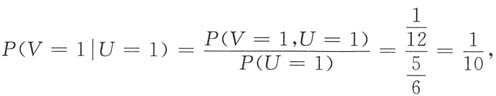 所以所求V的分布律为
所以所求V的分布律为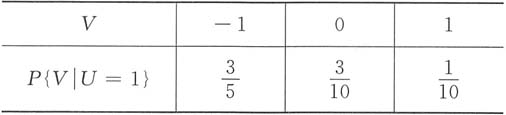
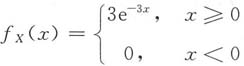 ,求随机变量
,求随机变量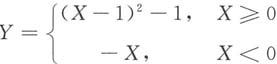 的分布函数FY(y).
的分布函数FY(y).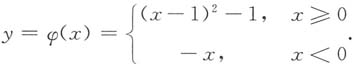

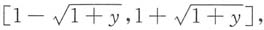
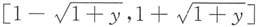 上的积分为
上的积分为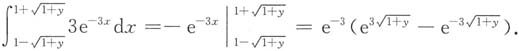
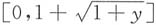 ,此时
,此时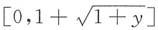 上的积分为
上的积分为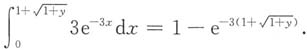 综上所述,y的分布函数为
综上所述,y的分布函数为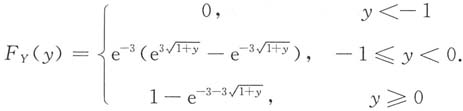
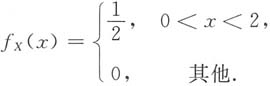
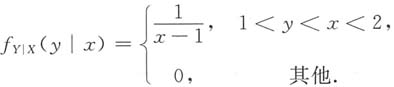 再根据条件概率密度的定义,可得联合概率密度
再根据条件概率密度的定义,可得联合概率密度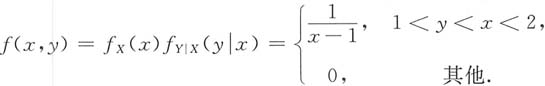
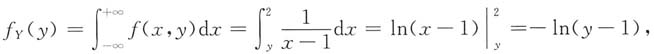 所以
所以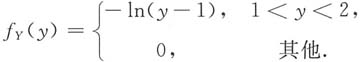 由于fX(x)fY(y)≠f(x,y),所以X与Y不独立.
由于fX(x)fY(y)≠f(x,y),所以X与Y不独立.
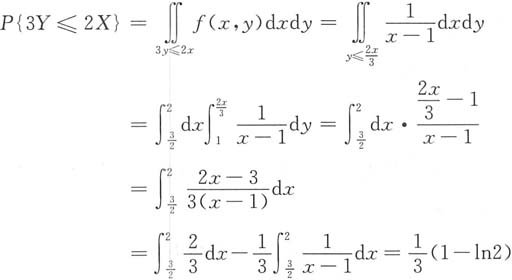
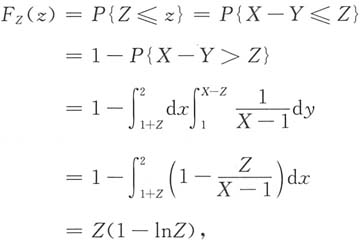
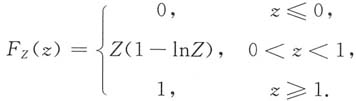
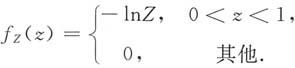
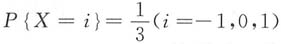 ,Y的概率密度函数为
,Y的概率密度函数为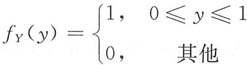 ,设Z=X+Y.
,设Z=X+Y.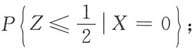
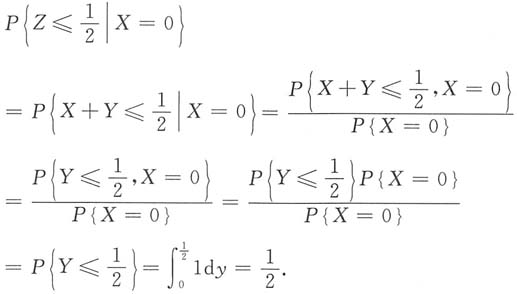
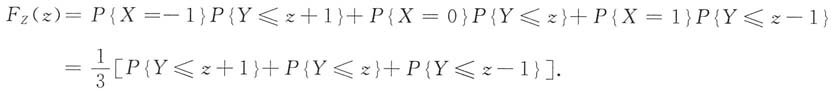
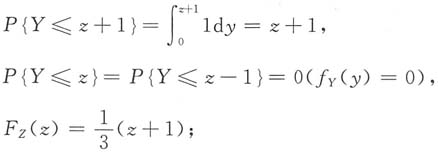

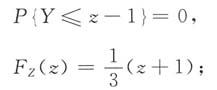
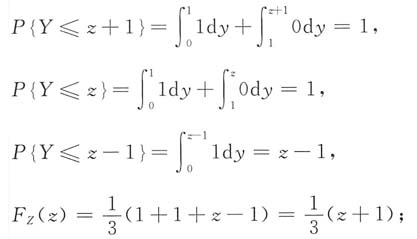
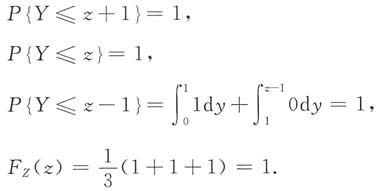
 故
故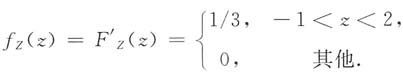
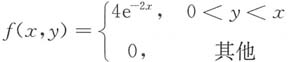 ,令随机变量U=X+Y,V=X-Y.
,令随机变量U=X+Y,V=X-Y.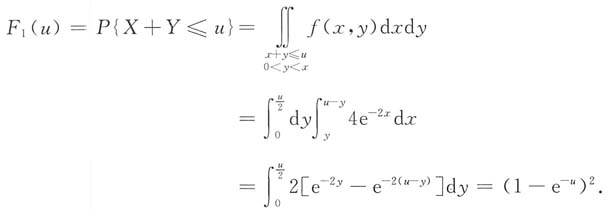 故U的分布函数F1(u)为
故U的分布函数F1(u)为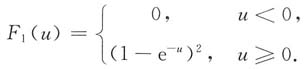

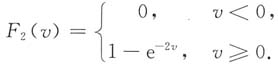
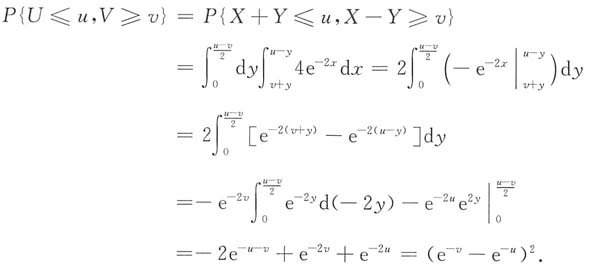
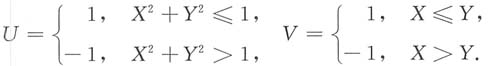

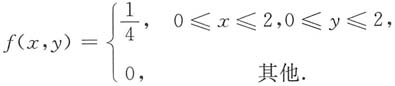 则有
则有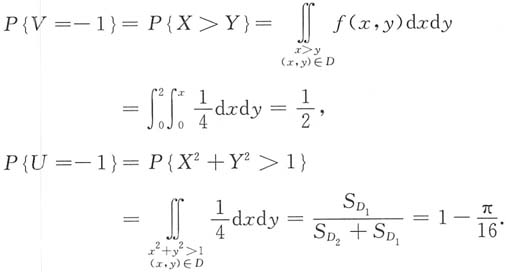
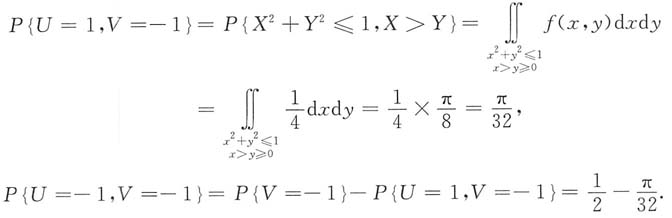

 所以E(UV)=E(U)·E(V),U与V不相关;又因为P{U=u,V=v}=P{U=u}·P{V=v},所以U与V相互独立.
所以E(UV)=E(U)·E(V),U与V不相关;又因为P{U=u,V=v}=P{U=u}·P{V=v},所以U与V相互独立.