一、选择题下列每题给出的四个选项中,只有一个选项是符合题目要求的.
1. 设f(x)=ln(1+x
2)-x
2,

,则当x→0时f(x)是g(x)的______
- A.低阶无穷小量.
- B.高阶无穷小量.
- C.同阶但不等价的无穷小量.
- D.等价无穷小量.
A B C D
D
[解析]
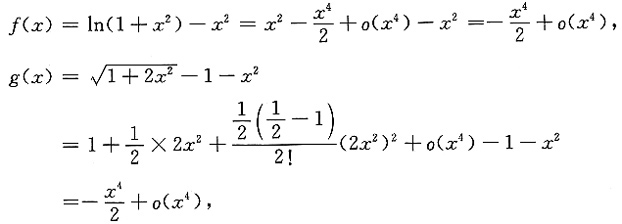
则
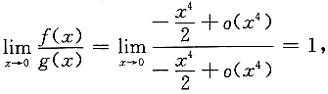
所以,当x→0时,f(x)是g(x)的等价无穷小量.
8. 已知r(A)=r
1,且方程组AX=α有解,r(B)=r
2,且BY=β无解,设A=(α
1,α
2,…,α
n),B=(β
1,β
2,…,β
n),且r(α
1,α
2,…,α
n,α,β
1,β
2,…,β
n,β)=r,则______
- A.r=r1+r2.
- B.r>r1+r2.
- C.r=r1+r2+1.
- D.r≤r1+r2+1.
A B C D
D
[解析] 由题设
r(α1,α2,…,αn,α)=r1,
r(β1,β2,…,βn,β)=r2+1,
故r(α1,α2,…,αn,α,β1,β2,…,βn,β)≤r(α1,α2,…,αn,α)+r(β1,β2,…,βn,β)
=r1+r2+1.
二、填空题1.

=______.
2. 设y"-2y'+ay=3e
-x的特解形式为Axe
-x,则其通解为______.
[解析] 因为方程有特解Axe
-x,所以-1为特征方程r
2-2r+a=0的一个特征根,即
(-1)
2-2×(-1)+a=0

a=-3,
所以特征方程为
λ
2-2λ-3=0,得λ
1=-1,λ
2=3.
齐次方程y"-2y'+ay=0的通解为
y=C
1e
-x+C
2e
3x(C
1,C
2为任意常数).
再把Axe
-x代入原方程,得
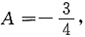
所以原方程的通解为
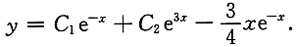
3.
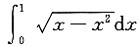
=______.
4. 设有一半椭球形水池,池口是半径为a的圆,若以每秒v单位的速度向池内注水,则水深增加的速度
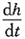
与水深h的关系是______.
[解析] 如图,建立坐标系,设水深为h的水面圆的半径为x,则椭圆方程为
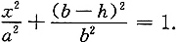
此时,池中水量增量微元为
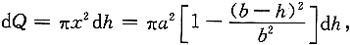
从而
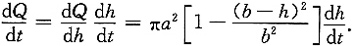
由于
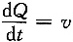
,故有
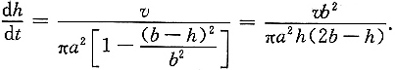
5. 设区域D={(x,y)|0≤x≤1,0≤y≤1),f(x)为D上的正值连续函数,a,b为常数,则
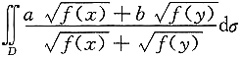
=______.
6. 已知二次型
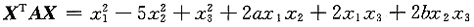
的秩为2,(2,1,2)
T是A的特征向量,那么经正交变换后二次型的标准形是______.
[解析] 求二次型X
TAX在正交变换下的标准形,也就是求二次型矩阵A的特征值.
设α
1=(2,1,2)
T,根据特征值定义Aα=λα得
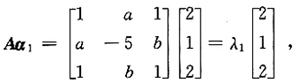
即
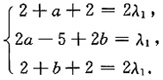
解出a=b=2,λ
1=3.
又r(X
TAX)=2,知|A|=0,于是λ
2=0是A的特征值.
再由∑a
ii=∑λ
i,有1+(-5)+1=3+0+λ
3,于是λ
3=-6是A的特征值.
因此,正交变换下二次型的标准形为

.
三、解答题共94分.解答应写出文字说明、证明过程或演算步骤.
1. 已知函数f(x)在(0,+∞)内可导,f(x)>0,
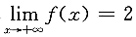
,且满足
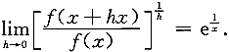
求f(x).
[解析]
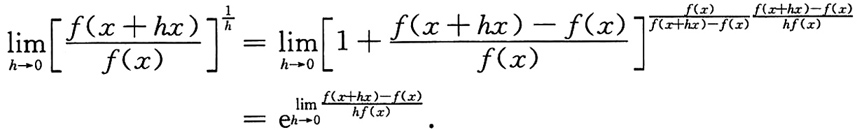
由导数定义,有
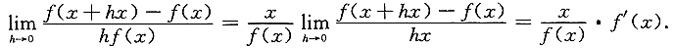
由已知得
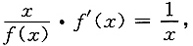
即
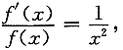
积分得
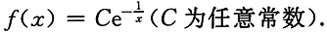
又
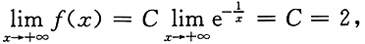
则
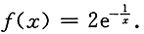
2. 设f(x)在(a,+∞)内可导,且
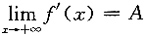
,求证:
若A>0,则
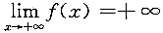
;若A<0,则

;
[解析] 联系f(x)与f'(x)的是拉格朗日中值定理,取x
0∈(a,+∞),
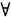
x>x
0有
f(x)=f(x
0)+f'(ξ)(x-x
0)(x
0<ξ<x). ①
因
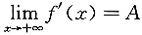
,若A>0,由极限的不等式性质可得,
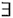
X>a,当x>X时,
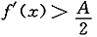
.现取定x
0>X,当x>x
0时,由于ξ>x
0>x,有
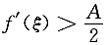
,于是由式①得
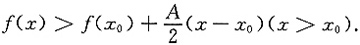
又因为
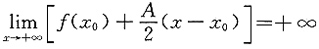
,所以

若A<0,考察h(x)=-f(x),则h'(x)=-f'(x),从而
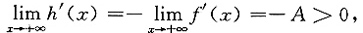
由已证结论知
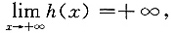
于是
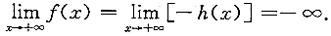
3. 设g(x)在[a,+∞)上连续,且
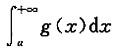
收敛,又
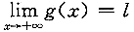
,求证l=0.
[解析] 记
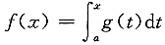
,则f(x)在[a,+∞)内可导且
f'(x)=g(x),
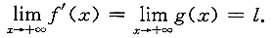
若l≠0,则l>0或l<0,由(Ⅰ)中结论得
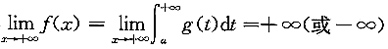
,与
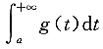
收敛矛盾.因此l=0.
4. 设函数z=f(x,y)在点(1,1)处可微,且
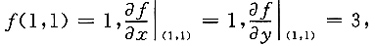
φ(x)=f[x,xf(x,x)],求
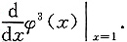
[解析] φ(1)=f(1,1)=1,

归结为求φ'(1).
根据复合函数求导法得
φ'(x)=f'
1[x,xf(x,x)]+f'
2[x,xf(x,x)]·
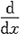
[xf(x,x)]
=f'
1[x,xf(x,x)]+f'
2[x,xf(x,x)]·{f(x,x)+x[f'
1(x,x)+f'
2(x,x)]),
φ'(1)=f'
1(1,1)+f'
2(1,1)[1+f'
1(1,1)+f'
2(1,1)],
又
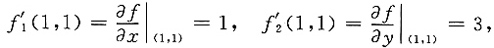
所以
φ'(1)=1+3×(1+1+3)=16,

5. 设曲线L位于xOy平面的第一象限内,L上任意一点M处的切线与y轴总相交,交点为A,已知|MA|=|OA|,且L经过点(1,1),求L的方程.
[解析] 设点M的坐标为(x,y),则切线MA:Y-y=y'(X-x),令X=0,则Y=y-y'x,故点A的坐标为(0,y-y'x).
由|MA|=|OA|得
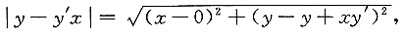
即
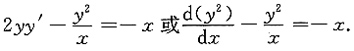
这是一阶线性非齐次方程,解得
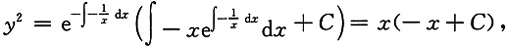
因为曲线经过点(1,1),所以C=2.
再由曲线在第一象限内,得曲线方程为
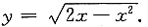
6. 设f(x)在[0,a]上有一阶连续导数,证明:至少存在一点ξ∈[0,a],使得

[解析] 所给问题为f(x)的定积分与f'(ξ)之间的关系,可以考虑成其原函数
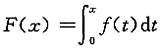
与F"(ξ)之间的关系,从而利用二阶泰勒公式来证明.
如果认定为考查f(x)与f'(ξ)之间的关系,也可以利用拉格朗日中值定理(一阶泰勒公式)来证明.
也可以利用积分中值定理
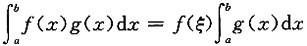
来证明.
思路一:
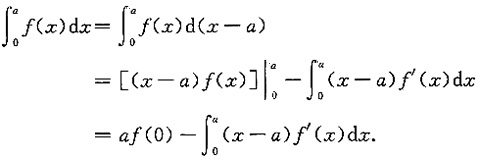
因为f'(x)连续,x-a≤0(x∈[0,a]),故由积分中值定理知,至少存在一点ξ∈[0,a],使得
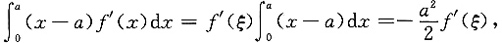
于是
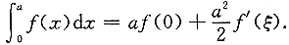
思路二:令
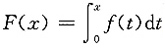
,则F(x)可用麦克劳林公式表示为
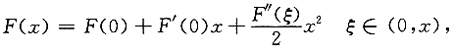
即
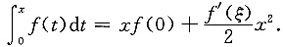
令x=a,得
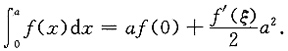
7. 求水池中原来水的体积;
[解析] 如图,建立直角坐标系,以球心为坐标原点,向上作为y轴正向.取区间[y,y+dy],在此区间上,体积微元
dV=πx
2dy,
其中
x
2=4
2-y
2,
所以
dV=π(16-y
2)dy,
水的体积为
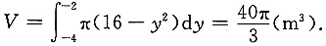

8. 求抽水至少需要做多少功.
[解析] 提升体积微元的水所需的功为
dW=(6-y)ρgπ(16-y
2)dy,
所以,将水全部提升至地面上方6m处,需做功
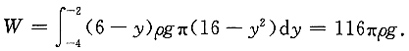
9. 计算
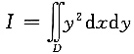
,其中D是由直线x=-2,y=2,x轴及曲线
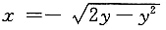
所围成.
[解析] 积分区域如图所示.
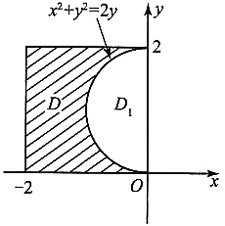
选择先x后y的积分次序,得
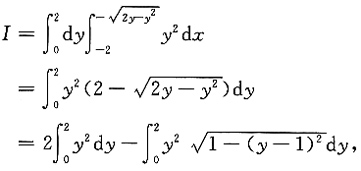
令t=y-1,得
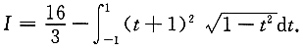
利用对称区间上奇偶函数积分性质及定积分几何意义,可得
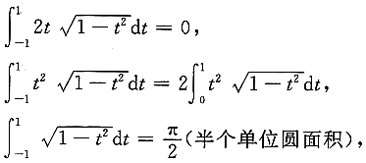
所以
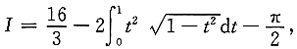
令t=sinθ,得
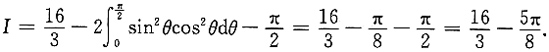
10. 证明:至少存在一个非零向量可同时由α
1,α
2和β
1,β
2线性表示;
[解析] 因为α
1,α
2,β
1,β
2线性相关,所以存在不全为零的常数k
1,k
2,l
1,l
2,使得
k
1α
1+k
2α
2+l
1β
1+l
2β
2=0

k
1α
1+k
2α
2=-l
1β
1-l
2β
2.
令
γ=k
1α
1+k
2α
2=-l
1β
1-l
2β
2,
因为α
1,α
2与β
1,β
2都线性无关,k
1,k
2及l
1,l
2不全为零,所以γ≠0.
11. 设
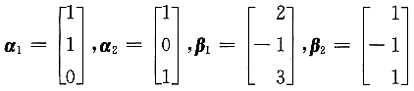
,求出可由两组向量同时线性表示的向量.
[解析] 令k
1α
1+k
2α
2+l
1β
1+l
2β
2=0,用初等变换法解此齐次方程组
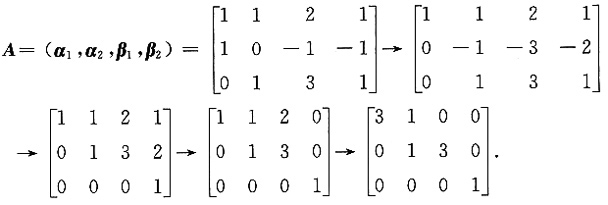
则
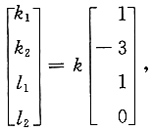
所以
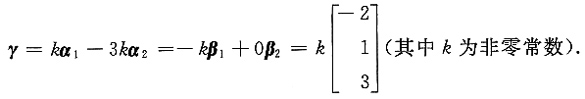
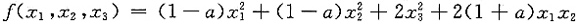 的秩为2.
的秩为2.12. 求a的值;
[解析] 二次型对应矩阵为
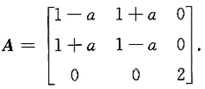
由二次型的秩为2,知
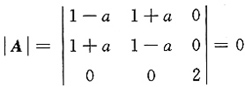
,得a=0.
13. 求正交变换x=Qy,把f(x
1,x
2,x
3)化成标准形;
[解析] 当a=0时,
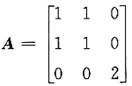
,可求出特征值为λ
1=λ
2=2,λ
3=0.
解(2E-A)x=0,得特征向量为
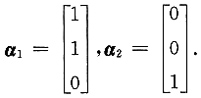
解(0E-A)x=0,得特征向量为
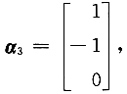
由于α
1,α
2,α
3已经正交,直接将α
1,α
2,α
3单位化,得
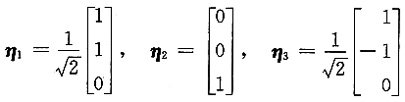
令Q=[η
1,η
2,η
3],即为所求的正交变换矩阵,由x=Qy,可化原二次型为标准形
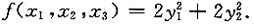
14. 求方程f(x
1,x
2,x
3)=0的解.
[解析] 由
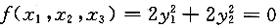
,得y
1=0,y
2=0,y
3=k(k为任意常数),从而所求解为
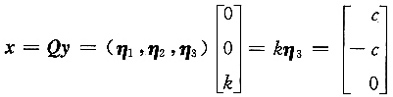
,其中c为任意常数.
 ,则当x→0时f(x)是g(x)的______
,则当x→0时f(x)是g(x)的______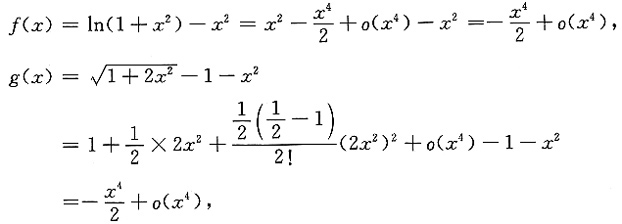
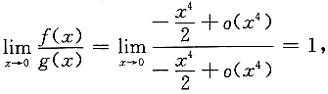
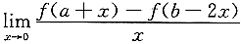 =______.
=______.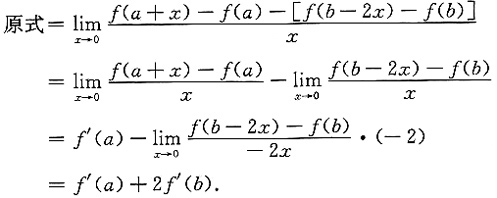
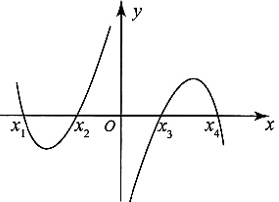

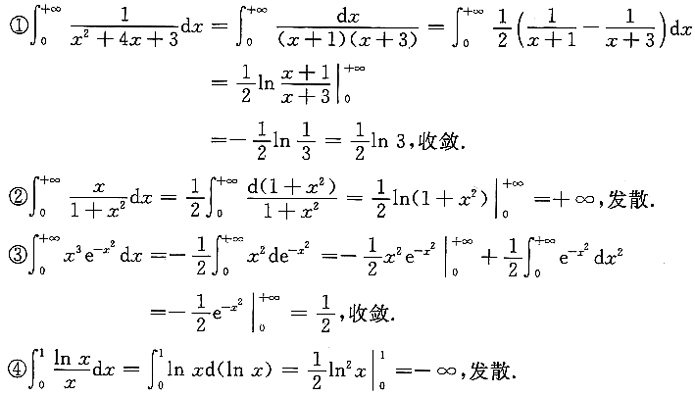
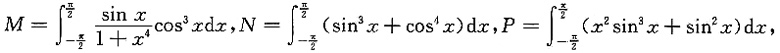 则有______
则有______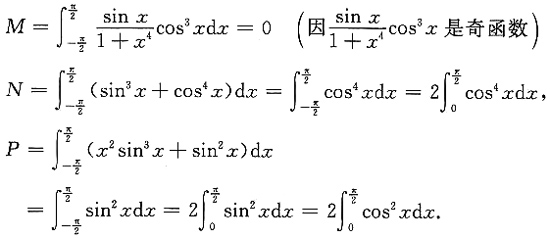
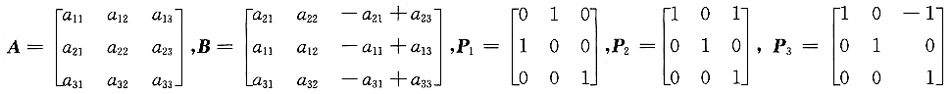 ,其中A可逆,那么B-1=______
,其中A可逆,那么B-1=______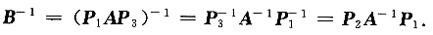
 =______.
=______.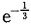

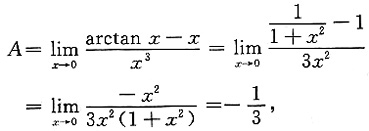
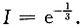
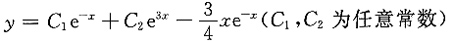
 a=-3,
a=-3,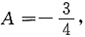
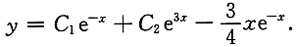
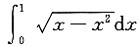 =______.
=______.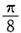
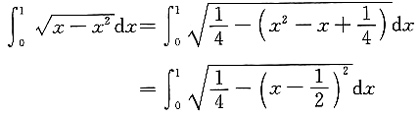
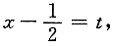
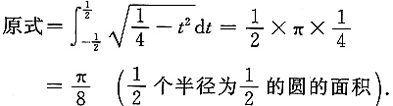
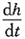 与水深h的关系是______.
与水深h的关系是______.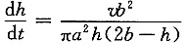
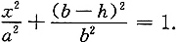
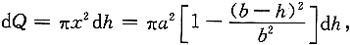
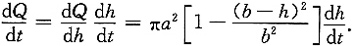
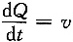 ,故有
,故有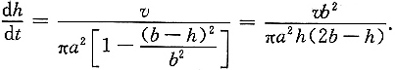
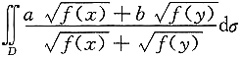 =______.
=______.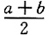
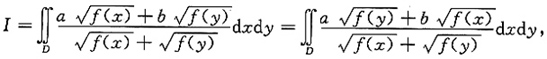
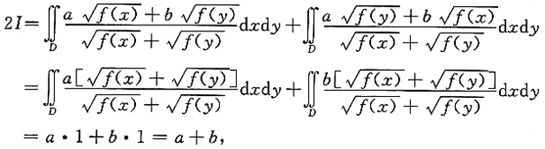
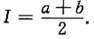
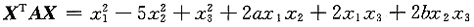 的秩为2,(2,1,2)T是A的特征向量,那么经正交变换后二次型的标准形是______.
的秩为2,(2,1,2)T是A的特征向量,那么经正交变换后二次型的标准形是______.
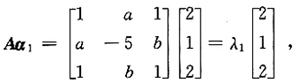
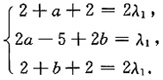
 .
.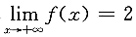 ,且满足
,且满足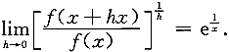
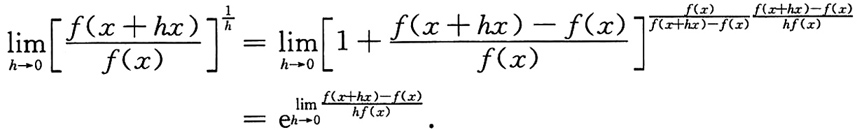
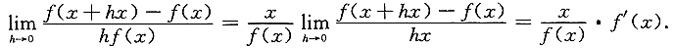
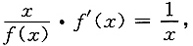
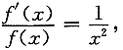
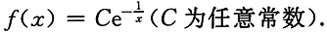
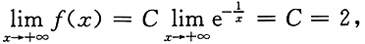
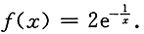
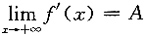 ,求证:
,求证: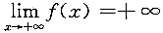 ;若A<0,则
;若A<0,则 ;
;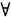 x>x0有
x>x0有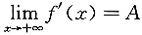 ,若A>0,由极限的不等式性质可得,
,若A>0,由极限的不等式性质可得,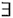 X>a,当x>X时,
X>a,当x>X时,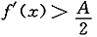 .现取定x0>X,当x>x0时,由于ξ>x0>x,有
.现取定x0>X,当x>x0时,由于ξ>x0>x,有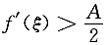 ,于是由式①得
,于是由式①得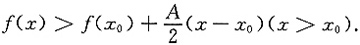
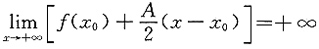 ,所以
,所以
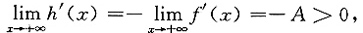
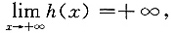
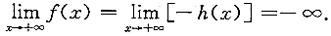
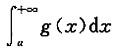 收敛,又
收敛,又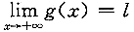 ,求证l=0.
,求证l=0.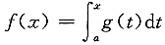 ,则f(x)在[a,+∞)内可导且
,则f(x)在[a,+∞)内可导且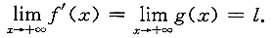
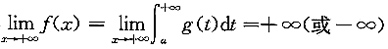 ,与
,与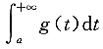 收敛矛盾.因此l=0.
收敛矛盾.因此l=0.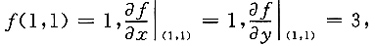 φ(x)=f[x,xf(x,x)],求
φ(x)=f[x,xf(x,x)],求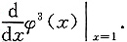

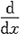 [xf(x,x)]
[xf(x,x)]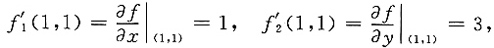

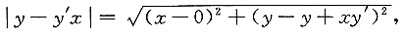
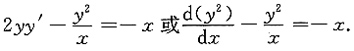
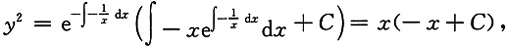
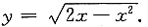

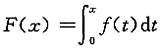 与F"(ξ)之间的关系,从而利用二阶泰勒公式来证明.
与F"(ξ)之间的关系,从而利用二阶泰勒公式来证明.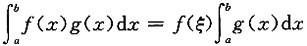 来证明.
来证明.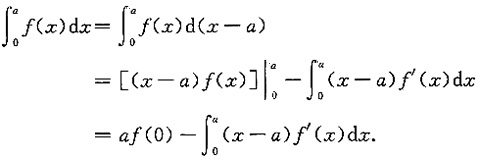
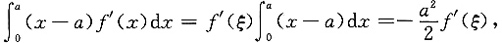
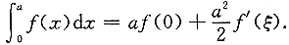
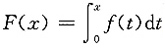 ,则F(x)可用麦克劳林公式表示为
,则F(x)可用麦克劳林公式表示为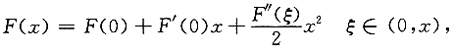
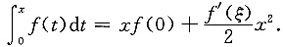
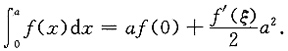
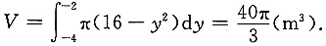

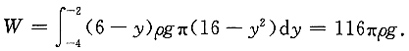
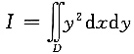 ,其中D是由直线x=-2,y=2,x轴及曲线
,其中D是由直线x=-2,y=2,x轴及曲线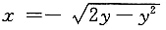 所围成.
所围成.
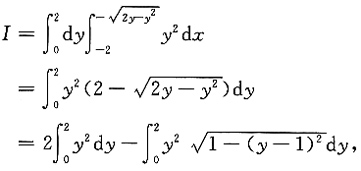
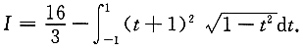
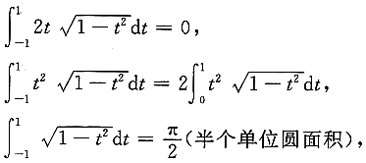
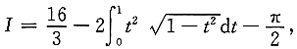
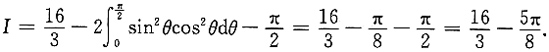
 k1α1+k2α2=-l1β1-l2β2.
k1α1+k2α2=-l1β1-l2β2.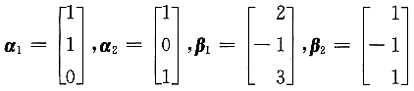 ,求出可由两组向量同时线性表示的向量.
,求出可由两组向量同时线性表示的向量.

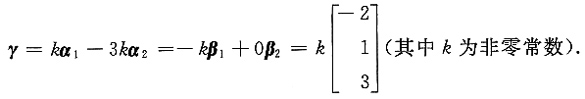
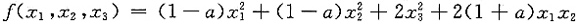 的秩为2.
的秩为2.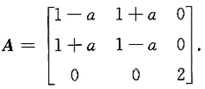
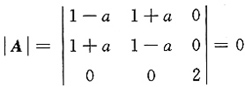 ,得a=0.
,得a=0.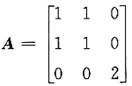 ,可求出特征值为λ1=λ2=2,λ3=0.
,可求出特征值为λ1=λ2=2,λ3=0.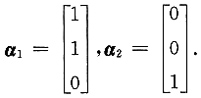
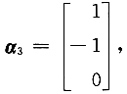
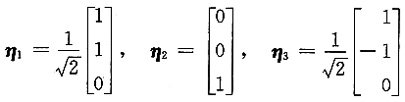
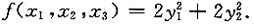
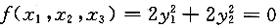 ,得y1=0,y2=0,y3=k(k为任意常数),从而所求解为
,得y1=0,y2=0,y3=k(k为任意常数),从而所求解为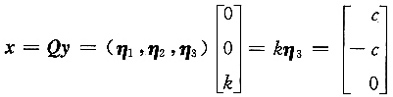 ,其中c为任意常数.
,其中c为任意常数.