选择题1. 有以下命题:

①

②

③

④

则以上命题中正确的个数是
A B C D
B
[解析] 举反例说明①,②,③均错,例如.

则
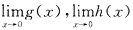
均不

,但

故②,③不正确.
若取f(x)=0,则

,故①也不正确.
按题设,易知
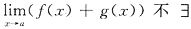
.(否则,若

,则
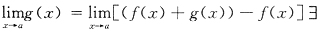
,矛盾).故④正确.选(B)
2. 设

,则下列命题中不正确的是
A.

B.

C.

D.

A B C D
B
[解析] 易知,两个正无穷大量之和与之积均是正无穷大量,即(A)、(D)正确.又正无穷大量与有界量之和仍为正无穷大量,即(C)也正确.因此,(B)不正确.选(B).
我们知道,当A=0时,

是未定式(无穷大量与无穷小量之积).因此(B)不正确.
3. 下列叙述正确的是
A.如果f(x)在x
0某邻域内无界,则

B.如果

,则f(x)在x
0某邻域内无界.
C.

不存在,则

D.如果

,则

A B C D
B
[解析] 因为

,所以,对于任意M>0,存在δ>0,当0<|x-x
0|<δ时,|f(x)|>M由此可得f(x)在x
0的某邻域内无界,因此选(B).
举反例说明(A)、(C)、(D)均不成立.设


,则x
n→0,y
n→0(n→∞)
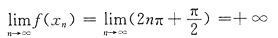
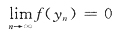

f(x)在x=0邻域无界,但x→0时f(x)不是无穷大量.也说明

.
此例说明A,C不正确.
若令f(x)=o(常数函数),则

,但

无定义,故D不正确.
因此选B.
4. 设有下列命题
①数列{x
n}收敛(即

极限

,则x
n有界.
②数列极限

其中l为某个确定的正整数.
③数列

④数列极限

则以上命题中正确的个数是
A B C D
C
[解析] 若极限

,则x
n有界.这是我们应熟悉的基本定理,即①正确.关于②,③的正确性,从直观上理解即可.
x
n:x
1,x
2,x
3,…,x
n,…
x
n+l:x
1+l,x
2+l,x
3+l,…,x
n+1,…
x
n中去掉前l项即x
n+l.
x
2n-1:x
1,x
3,x
5,…,x
2n-1,…
x
2n:x
2,x
4,x
6,…,x
2n,…
它们一起涵盖了x
n的所有项.
命题④是错的.例如

,但

因此选C.
5. 设x
n≤z
n≤y
n且

,则
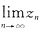
- A.存在且等于零.
- B.存在但不一定等于零.
- C.不一定存在.
- D.一定不存在.
A B C D
C
[解析] 由

.
又因

.但不保证
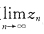
存在.例如,
取

,

,此时有x
n≤z
n≤y
n 且
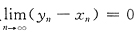
,但当n→∞时,z
n的极限不存在,因此选C.
6. 下列命题中正确的是
A.若

,当0<|x-x
0|<δ时f(x)≥g(x).
B.若

使得当0<|x-x
0|<δ时有f(x)>g(x)且

均

,则A
0>B
0.
C.若
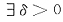
,当0<|x-x
0|<δ时
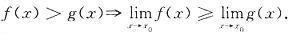
D.若
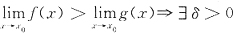
,当0<|x-x
0|<δ时有f(x)>g(x).
A B C D
D
[解析] D正确.D正是极限的不等式性质中所述的结论.A的错误在于由

不能判断x
0附近f(x)与g(x)的大小关系.由(B)的条件只能得A
0≥B
0.在C中没假设极限存在.选D.
8. 若

,则

为
A.0.
B.3.
C.

D.∞.
A B C D
C
[解析] 因为

又

所以

选C.
对sin3x
2用泰勒公式.由

令t=3x
2得

于是
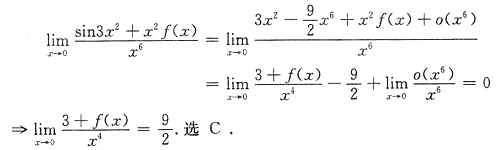
11. 下列各题计算过程中正确无误的是
A.

B.

C.

D.
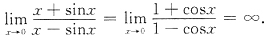
A B C D
D
[解析] A是错的.因为n是正整数,对数列没有导数概念,不能直接用洛必达法则.
B是错的.因为

已不是未定式,不能用洛必达法则.
C也是错的.用洛必达法则求

型极限

时,若

不存在,也不为∞,则法则失效,不能推出原极限不存在,事实上该极限是存在的.因此选D.
D是正确的.
用洛必达法则求

型极限

时,
若

(有限数),则

.
若

,D正是后一种情形.
A,B,C的正确解法是:
A.

B.

C.

12. 设x→0时ax
2+bx+c=cosx是比x
2高阶无穷小,其中a,b,c为常数,则
A.

B.
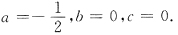
C.

D.
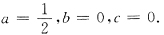
A B C D
C
[解析] 由题意得

得c=1
又因为
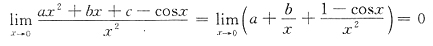
所以 b=0,

.因此选C.
因
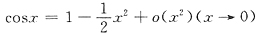
,于是

.
因此,

,b=0,c=1.选C.
13. 当x→0时下列无穷小中阶数最高的是
A.
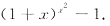
B.

C.
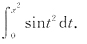
D.

A B C D
C
[解析] 逐一分析它们的阶.
A.(考察等价无穷小)
(1+x)
x2-1~ln[(1+x)
x2-1+1]=x
2ln(1+x)~x
3(x→0),

(1+x)
x2-1是x的3阶无穷小.
B.(考察等价无穷小).

是x的1阶无穷小.
C.(待定阶数法).

是x的6阶无穷小.
D.(待定阶数法或泰勒公式法)

是x的2阶无穷小.
或用泰勒公式.已知
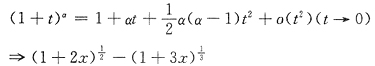

是x的2阶无穷小.
因此选C.
14. 设x→a时f(x)与g(x)分别是x-a的n阶与m阶无穷小,则下列命题中,正确的个数是
①f(x)g(x)是x-a的n+m阶无穷小.
②若n>m,则

是x-a的n-m阶无穷小.
③若n≤m,则f(x)+g(x)是x-a的a阶无穷小.
④若f(x)连续,则

是x-a的n+1阶无穷小.
A B C D
C
[解析] 此类问题要逐一分析,按无穷小阶的定义:

是(x-a)的n+m阶无穷小;
又,若n>m,

是(x-a)的n-m阶无穷小;
因此①,②正确.再考察

由此得,当n<m时f(x)+g(x)是x-a的n阶无穷小.
当n=m时f(x)+g(x)是x-a的n阶(A+B≠0)或高于n阶(A+B=0)的无穷小.
例如,x→0时,sinx与-x均是x的一阶无穷小,但

即sinx+(-x)是x的三阶无穷小;
因此③不正确.
最后考察

是x-a的n+1阶无穷小.因此④正确.选C.
15. 以下极限等式(若右端极限存在,则左端极限存在且相等)成立的个数是
(1)设

且f
1(x)~f
2(x)(x→a),又

,则

(2)设

,f
i(x)>0,(0<|x-a|<δ),i=1,2,且f
1(x)~f
2(x),g
1(x)~g
2(x)(x→a),则
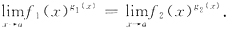
(3)设
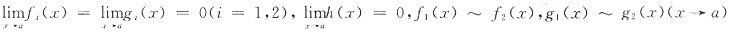
又

,则

A B C D
D
[解析] 要逐一分析.我们证明(1),(2),(3)成立.
关于(1)

其中

这里ln(1+f
i(x))~f
i(x))(x→a,i=1,2)
关于(2)

关于(3)可直接证明:

因此

选D.
16. 设f(x)对一切x
1,x
2满足f(x
1+x
2)=f(x
1)+f(x
2),f(x)在x=0连续.设x
0≠0为任意实数,则
- A.limf(x)不存在.
- B.limf(x)存在,但f(x)在x0不连续.
- C.f(x)在x0连续.
- D.f(x)在x0的连续性不确定.
A B C D
C
[解析] 按定义考察f(x)在x
0的连续性,即考察

.由条件得
f(x
0+Δx)=f(x
0)+f(Δx)
又由f(x)在x=0连续
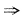

f(x)在x
0是否连续,取决于f(0)是否为零。由
f(x
1+x
2)=f(x
1)+f(x
2)
若令x
2=0
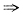
f(x
1)=f(x
1)+f(0)

f(0)=0
因此

f(x)在x
0连续.选C.
17. 设

则
- A.x=0与x=1都是f(x)的第一类间断点.
- B.x=0与x=1都是f(x)的第二类间断点.
- C.x=0是f(x)的第一类间断点,x=1是f(x)的第二类间断点.
- D.x=0是f(x)的第二类间断点,x=1是f(x)的第一类间断点.
A B C D
C
[解析]
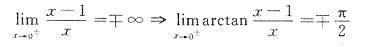
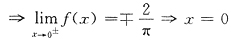
是f(x)的第一类间断点.
又
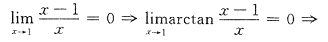
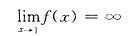

x=1是f(x)的第二类间断点.
因此选C.
18. 设数列极限函数

,则f(x)的定义域I和f(x)的连续区间J分别是
- A.I=(-∞,+∞),J=(-∞,+∞).
- B.1=(-1,+∞),J=(-1,1)∪(1,+∞).
- C.I=(-1,+∞),J=(-1,+∞).
- D.I=(-1,1),J=(-1,1).
A B C D
B
[解析] |x|<1时,

x=1时

x>1时

x≤-1时

x=1时

无定义.
因此,f(x)在x≤-1无定义.

f(x)的连续区间是
J=(-1,1)∪(1,+∞).
19. 设f(x)在点x
0的某邻域内有定义,且f(x)在x
0间断,则在点x
0处必定间断的函数是
- A.f(x)sinx.
- B.f(x)+sinx.
- C.f2(x).
- D.|f(x)|.
A B C D
B
[解析] 若f(x)+sinx在x=x
0连续

f(x)=(f(x)+sinx)-sinx
在x=x
0连续,与已知矛盾.因此f(x)+sinx在x
0必间断.选B.
举反例说明A,C,D不对.
设

则f(x)在x=0间断,

在x=0连续.
若设

在x=0间断,但
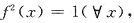

在x=0均连续,因此不选A,C,D.
20. “f(x)在x
0点连续”是|f(x)|在x
0点连续的
- A.充分条件,但不是必要条件.
- B.必要条件,但不是充分条件.
- C.充分必要条件.
- D.既不是充分,也不是必要条件.
A B C D
A
[解析] 由“若

,则

”可得“如果

,则

”因此,f(x)在x
0连续,则|f(x)|在x
0连续,但|f(x)|在x
0处连续,f(x)在x
0处不一定连续.
如

在x=0不连续,但|f(x)|=1在x=0处连续.于是应选A.
21. 设f(x)=g(x)φ(x),其中g(x),φ(x)在x=x
0邻域U有定义,g(x)在x=x
0连续,φ(x)在x=x
0不连续,但在U有界,则g(x
0)=0是f(x)在x=x
0连续的.
- A.充要条件.
- B.充分非必要条件.
- C.必要非充分条件.
- D.既非充分也非必要条件.
A B C D
A
[解析] 若g(x
0)=0,由假设条件:

,φ(x)在x
0邻域∪有界


f(x)在x=x
0连续.
若f(x)在x=x
0连续,可证g(x
0)=0,若g(x
0)≠0,

在x=x
0连续,与已知矛盾.因此g(x
0)=0.选A.
22. f(x)在x
0处存在左、右导数,则f(x)在x
0点
A B C D
B
[解析] 直接从条件出发,由f'+(x
0),f'-(x
0)均

在x=x
0既左又右连续,
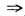
(x)在x=x
0连续,因此选B.
23. 下列命题中正确的个数是
①φ(x)在x=x
0连续,f(u)在u
0=φ(x
0)连续,则f(φ(x))在x=x
0连续.
②φ(x)在x=x
0连续,f(u)在u
0=φ(x
0不连续,f(φ(x))在x=x
0不连续.
③φ(x)在x=x
0不连续,f(u)在u
0=φ(x
0连续,则f(φ(x))在x=x
0不连续.
④φ(x)在x=x
0不连续,f(u)在u
0=φ(x
0不连续,则f(φ(x))在x=x
0可能连续.
A B C D
B
[解析] 在复合函数连续性问题的结论中,只有一个结论是确定的,即结论①是正确的,其余情形则结论不确定,因而②,③是错误的,而④是正确的.因此选B.
24. 设

,则
- A.f(x)在(-∞,0]有界,在[0,+∞)无界.
- B.f(x)在(-∞,0]无界,在[0,+∞)有界.
- C.f(x)在(-∞,0],[0,+∞)均有界.
- D.f(x)在(-∞,0],[0,+∞)均无界.
A B C D
B
[解析] 显然f(x)在(-∞,+∞)可导,为考察f(x)在[0,+∞)或(-∞,0]的有界性问题,我们需要求极限

.
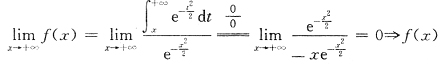
在[0,+∞)有界
注意

无界.
因此选B.
25. 设f(x)在[a,+∞)连续,则“

”是f(x)在[a,+∞)无界的
- A.充分非必要条件.
- B.必要非充分条件.
- C.充要条件.
- D.既非充分又非必要条件.
A B C D
C
[解析] 若

x
n∈[a,+∞)使得

,

,则f(x)在[a,+∞)无界.若f(x)在[a,+∞)有界,即|f(x)|≤M(x∈[a,+∞))

|f(x
n)|≤M与

矛盾.
若f(x)在[a,+∞)无界
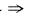
对
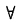
自然数n,f(x)在[n,+∞)无界

x
n∈[n,+∞),

.因此选C.
26. 下列函数中在[1,+∞)无界的是
A.

B.

C.

D.

A B C D
C
[解析] 直接指出某函数在[1,+∞)无界.取x
n=n
2π
2,
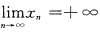
,对于C.
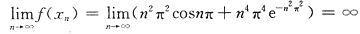
,

C中f(x)在[1,+∞)无界.
指出三个函数在[1,+∞)有界.对于A,B,D中f(x)均在[1,+∞)连续,又
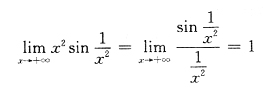
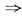
A有界.
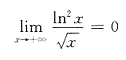

有界

有界,即B在[1,+∞)有界.
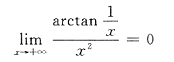

D在[1,+∞)有界.因此选C.
27. 设α是实数

,f(x)在x=1处可导,则α的取值为
- A.α<-1.
- B.-1≤α<0.
- C.0≤α<1.
- D.α≥1.
A B C D
A
[解析] 显然,f'-(1)=0.由右导数定义

(当α+1≥0时该极限不存在).
因此,仅当α+1<0,即α<-1时,f'(1)存在(f'(1)=0).因此选A.

不存在,但

是有界量,又

要使

存在,必须

,此处利用了无穷小量与有界量的乘积是无穷小量.
29. 设f(x)有二阶连续导数,且f(0)=f'(0)=0,f"(x)>0,又设u=u(x)是曲线y=f(x)在点(x,f(x))处的切线在x轴上的截距,则
A.1.
B.2.
C.

D.0.
A B C D
B
[解析] 任取x
0≠0,则曲线y=f(x)在x
0处的切线方程为y-f(x
0)=f'(x
0)(x-x
0),令y=0得它在x轴上截距为:

.因此,曲线y=f(x)在点(x,f(x))的切线在z轴上的截距为

,下求
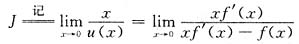

由于

于是

方法2 直接用洛必达法则求这个

型极限
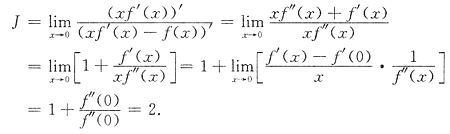
因此选B.
方法3 用泰勒公式

代入得

因此选B.
34. 设y=f(x)在(a,b)可微,则下列结论中正确的个数是
①

与Δx是同阶无穷小.
②df(x)只与x∈(a,b)有关.
③Δy=f(x+Δx)-f(x),则dy≠Δy.
④Δx→0时,dy-Δy是Δx的高阶无穷小.
A B C D
B
[解析] 要逐一分析.
因为
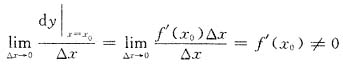

与Δx是同阶无穷小,①正确.
df(x)=f'(x)Δx,df(x)与x∈(a,b)及Δx有关,故②不正确.
当y=f(x)为一次函数:f(x)=ax+b,

dy=aΔx-Δy.故③不正确.
由可微概念,
f(x+Δx)-f(x)=f'(x)Δx+o(Δx)(Δx→0)
即Δy-dy=0(Δx)(Δx→0)故④正确.因此,选B.
36. 设f(x)在x=0可导,且

,则f'(0)=
A.ln2.
B.

C.1.
D.2.
A B C D
B
[解析] 由条件

.再由f(x)的连续性

f(0)=0.
现用等价无穷小因子替换

选B.
37. 设f(x)在x=x
0连续且满足
f(x)=2(x-x
0)+o((x-x
0)) (x→x
0)
则y=f(x)在x=x
0处的微分

当x→x
0时是(x-x
0)的
- A.同阶非等价无穷小.
- B.等价无穷小.
- C.高阶无穷小.
- D.低阶无穷小.
A B C D
A
[解析] 按题设

.于是,题设可写成
f(x)-f(x
0)=2(x-x
0)+o((x-x
0))(x→x
0)
按微分的定义

因此选A.
38. 设x=y-εsiny(0<ε<1为常数),它的反函数是y=y(x),则

A.

B.

C.

D.

A B C D
C
[解析] 用反函数求导法先求出

再由复合函数求导法得

选C.
39. 设

,则
- A.f(x)在x=x0。处必可导且f'(x0)=a.
- B.f(x)在x=x0处必连续,但未必可导.
- C.f(x)在x=x0处必有极限但未必连续.
- D.以上结论都不对.
A B C D
D
[解析] 首先将f(x)在x=x
0处的左右导数

与f'(x)在x=x
0处的左右极限

区分开来.
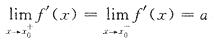
,只能得出

,但不能保证f(x)在x
0处可导,以及在x=x
0处连续和极限存在.
例如

显然,x≠0时,f'(x)=1因此

但

因而
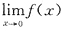
不存在,因此f(x)在x=0处不连续,不可导.
因此选D.
40. 设

为大于零的常数,h(x)在x
0无定义,

均存在,则g(x
0)=a,g'
-(x
0)=b是f(x)在x
0可导的
- A.充分非必要条件.
- B.必要非充分条件.
- C.充分必要条件.
- D.非充分非必要条件.
A B C D
C
[解析] 首先考察f(x)在x=x
0的连续性.
f(x)在x=x
0连续
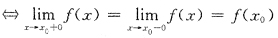

,则g(x)在x=x
0左连续).

补充定义h(x
0)=a,则

当g(x
0)=a时

因此在题设条件下,f(x)在x=x
0可导

.选C.
41. 以下四个结论中正确的是:
- A.设f(x)在[-a,a]是偶函数,f'+(0)存在,则f'(0)存在.
- B.设f(x)在[-a,a]是偶函数,则x=0是f(x)的极值点.
- C.设f(x)在[-a,a]是奇函数,f'+(0)存在,则f'(0)存在.
- D.设f(x)在x=x0可导,则曲线y=f(x)在(x0,f(x0))处存在切线,反之亦然.
A B C D
C
[解析] C是正确的.
设f(x)在[-a,a]是奇函数

f(0)=0.因存在
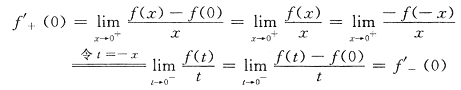

.选C.
A,B,D不正确.
如下图所示,f(x)在[-a,a]是偶函数,

,故f'(0)不存在.

如

,在[-a,a]是偶函数,但x=0不是极值点.

在x=0有垂直于x轴的切线,

在x=0不可导.
因此,A,B,D不正确,选C.
43. 设连续函数F(x)=g(x)φ(x),x=a是φ(x)的跳跃间断点,g'(a)存在,则g(a)=0,g'(a)=0是F(x)在x=a处可导的
- A.充分必要条件.
- B.充分非必要条件.
- C.必要非充分条件.
- D.非充分非必要条件.
A B C D
A
[解析] 因φ(x)在x=a不可导,所以不能对F(x)用乘积的求导法则,用定义求F'(a).题设φ(x)以x=a为跳跃间断点,则存在
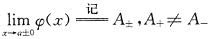
.
当g(a)=0时

这表明,g(a)=0时,F'(a)存在

下面证明若F'(a)存在则g(a)=0.
反证法,若g(a)≠0,
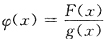
,由商的求导法则,φ(x)在x=a处可导,这与题设矛盾,所以选A.
44. 函数f(x)-(x
2+x-2)|sin2πx在

区间上不可导点的个数是
A B C D
B
[解析] 设g(x)=x
2+x-2,φ(x)=|sin2πx|,显然g(x)处处可导,φ(x)处处连续,有不可导点.
由类似可证:若g(x)在x=a处可导,φ(x)在x=a处连续但不可导,则当g(a)≠0时g(x)φ(x)在x=a处不可导,当g(a)=0时,g(x)φ(x)在x=a处可导,且

,只须考察φ(x)不可导点处g(x)是否为零.
φ(x)=|sin2πx|的图形如下图所示,在

内只有不可导点x=0,

,1,其余均可导.

因为g(0)=-2≠0,

,g(1)=0.
所以f(x)=g(x)φ(x)在

处不可导,在x=1可导,其余点均可导.因此选B.
45. 如下四个函数中,在x=0处可导的函数是
A.

B.f(x)=arctan|x|.
C.
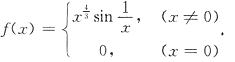
D.

A B C D
C
[解析] 已知|x|,

在x=0不可导.又x→0时,e
|x|-1~|x|,arctan|x|~|x|,

.
对A、B

对D

即A,B,D在x=0不可导.选C.
按导数定义,对C直接计算

选C.
47. 设

处处可导,则(a,b)等于
A.a任意,

B.

C.

D.

A B C D
B
[解析] 显然,x<0与x>0时对
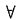
a,b之值f(x)均可导.关键是x=0处.
注意

首先要使f(x)在x=0连续.
由
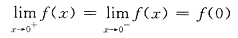
得

此时

再定b使f(x)在x=0可导.

由

得
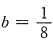
.因此选B.
48. 设

可出,则(b,c)=
A.(2,1).
B.(1,0).
C.
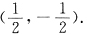
D.(3,2).
A B C D
A
[解析] |x|≠1时显然可导.由于f(x)是偶函数,故只须考察x=1.
首先要求f(x)在x=1连续,即

即

又


即4-2b=0
因此,b=2,c=1.选A.
49. 设直线y=ax+b同时与曲线y=x
2及

相切,则常数a=______,b=______.
- A.a=-4,b=-4.
- B.a=-3,b=-4.
- C.a=-4,b=-3.
- D.a=-3,b=-3.
A B C D
A
[解析] 设y=ax+b与y=x
2的切点为

与

的切点为

.
曲线y=x
2在

处的切线方程是

曲线

在切点

处的切线方程是

于是常数a,b同时满足
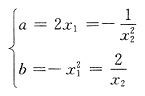

因此a=-4,b=-4.选A.
50. 在曲线

上任一点P(x,y)处作切线,该切线分别交x轴与y轴于A和B(如下图所示),则

A.

B.

C.

D.

的大小关系与P的位置有关.
A B C D
B
[解析] 任意点

处的切线方程是

即

其中(X,Y)为切线上点的坐标,分别令Y=0,X=0得A与B的坐标为(2x,0),

,于是

即

应选B.

 ②
②
 ④
④

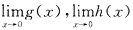 均不
均不 ,但
,但
 ,故①也不正确.
,故①也不正确.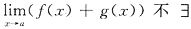 .(否则,若
.(否则,若 ,则
,则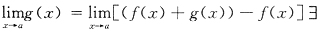 ,矛盾).故④正确.选(B)
,矛盾).故④正确.选(B) ,则下列命题中不正确的是
,则下列命题中不正确的是



 是未定式(无穷大量与无穷小量之积).因此(B)不正确.
是未定式(无穷大量与无穷小量之积).因此(B)不正确.
 ,则f(x)在x0某邻域内无界.
,则f(x)在x0某邻域内无界. 不存在,则
不存在,则
 ,则
,则
 ,所以,对于任意M>0,存在δ>0,当0<|x-x0|<δ时,|f(x)|>M由此可得f(x)在x0的某邻域内无界,因此选(B).
,所以,对于任意M>0,存在δ>0,当0<|x-x0|<δ时,|f(x)|>M由此可得f(x)在x0的某邻域内无界,因此选(B).
 ,则xn→0,yn→0(n→∞)
,则xn→0,yn→0(n→∞)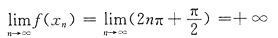
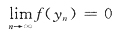
 f(x)在x=0邻域无界,但x→0时f(x)不是无穷大量.也说明
f(x)在x=0邻域无界,但x→0时f(x)不是无穷大量.也说明 .
. ,但
,但 无定义,故D不正确.
无定义,故D不正确. 极限
极限 ,则xn有界.
,则xn有界. 其中l为某个确定的正整数.
其中l为某个确定的正整数.

 ,则xn有界.这是我们应熟悉的基本定理,即①正确.关于②,③的正确性,从直观上理解即可.
,则xn有界.这是我们应熟悉的基本定理,即①正确.关于②,③的正确性,从直观上理解即可. ,但
,但
 ,则
,则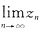
 .
. .但不保证
.但不保证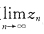 存在.例如,
存在.例如, ,
, ,此时有xn≤zn≤yn
,此时有xn≤zn≤yn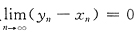 ,但当n→∞时,zn的极限不存在,因此选C.
,但当n→∞时,zn的极限不存在,因此选C. ,当0<|x-x0|<δ时f(x)≥g(x).
,当0<|x-x0|<δ时f(x)≥g(x). 使得当0<|x-x0|<δ时有f(x)>g(x)且
使得当0<|x-x0|<δ时有f(x)>g(x)且 均
均 ,则A0>B0.
,则A0>B0.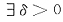 ,当0<|x-x0|<δ时
,当0<|x-x0|<δ时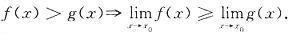
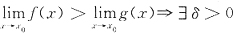 ,当0<|x-x0|<δ时有f(x)>g(x).
,当0<|x-x0|<δ时有f(x)>g(x). 不能判断x0附近f(x)与g(x)的大小关系.由(B)的条件只能得A0≥B0.在C中没假设极限存在.选D.
不能判断x0附近f(x)与g(x)的大小关系.由(B)的条件只能得A0≥B0.在C中没假设极限存在.选D.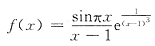 ,则当x→1时有
,则当x→1时有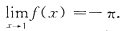
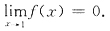
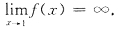
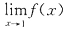 不存在,且
不存在,且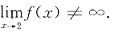
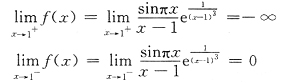
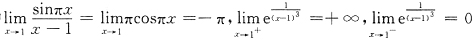 .
. ,因而
,因而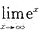 不存在.
不存在. ,则
,则 为
为


 选C.
选C.

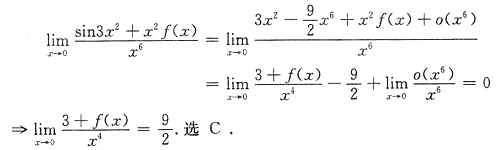
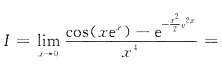
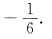
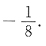
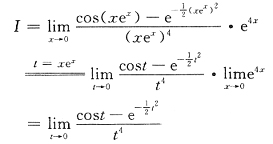
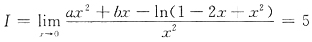 ,则
,则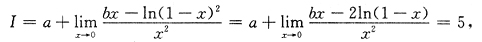
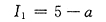
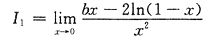



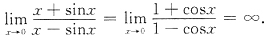
 已不是未定式,不能用洛必达法则.
已不是未定式,不能用洛必达法则. 型极限
型极限 时,若
时,若 不存在,也不为∞,则法则失效,不能推出原极限不存在,事实上该极限是存在的.因此选D.
不存在,也不为∞,则法则失效,不能推出原极限不存在,事实上该极限是存在的.因此选D. 型极限
型极限 时,
时, (有限数),则
(有限数),则 .
. ,D正是后一种情形.
,D正是后一种情形.



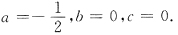

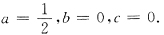

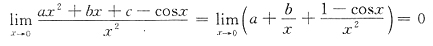
 .因此选C.
.因此选C.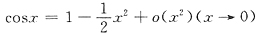 ,于是
,于是 .
. ,b=0,c=1.选C.
,b=0,c=1.选C.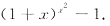

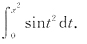

 (1+x)x2-1是x的3阶无穷小.
(1+x)x2-1是x的3阶无穷小. 是x的1阶无穷小.
是x的1阶无穷小. 是x的6阶无穷小.
是x的6阶无穷小. 是x的2阶无穷小.
是x的2阶无穷小.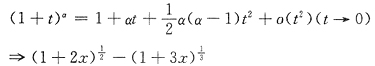
 是x的2阶无穷小.
是x的2阶无穷小. 是x-a的n-m阶无穷小.
是x-a的n-m阶无穷小. 是x-a的n+1阶无穷小.
是x-a的n+1阶无穷小. 是(x-a)的n+m阶无穷小;
是(x-a)的n+m阶无穷小; 是(x-a)的n-m阶无穷小;
是(x-a)的n-m阶无穷小;

 是x-a的n+1阶无穷小.因此④正确.选C.
是x-a的n+1阶无穷小.因此④正确.选C. 且f1(x)~f2(x)(x→a),又
且f1(x)~f2(x)(x→a),又 ,则
,则
 ,fi(x)>0,(0<|x-a|<δ),i=1,2,且f1(x)~f2(x),g1(x)~g2(x)(x→a),则
,fi(x)>0,(0<|x-a|<δ),i=1,2,且f1(x)~f2(x),g1(x)~g2(x)(x→a),则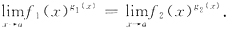
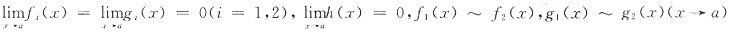 又
又 ,则
,则

 这里ln(1+fi(x))~fi(x))(x→a,i=1,2)
这里ln(1+fi(x))~fi(x))(x→a,i=1,2)


 .由条件得
.由条件得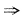

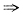
 f(0)=0
f(0)=0
 则
则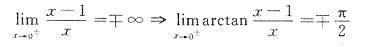
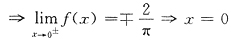 是f(x)的第一类间断点.
是f(x)的第一类间断点.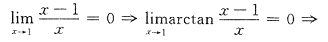
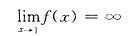
 x=1是f(x)的第二类间断点.
x=1是f(x)的第二类间断点. ,则f(x)的定义域I和f(x)的连续区间J分别是
,则f(x)的定义域I和f(x)的连续区间J分别是



 无定义.
无定义.
 f(x)=(f(x)+sinx)-sinx
f(x)=(f(x)+sinx)-sinx 则f(x)在x=0间断,
则f(x)在x=0间断, 在x=0连续.
在x=0连续. 在x=0间断,但
在x=0间断,但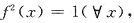
 在x=0均连续,因此不选A,C,D.
在x=0均连续,因此不选A,C,D. ,则
,则 ”可得“如果
”可得“如果 ,则
,则 ”因此,f(x)在x0连续,则|f(x)|在x0连续,但|f(x)|在x0处连续,f(x)在x0处不一定连续.
”因此,f(x)在x0连续,则|f(x)|在x0连续,但|f(x)|在x0处连续,f(x)在x0处不一定连续. 在x=0不连续,但|f(x)|=1在x=0处连续.于是应选A.
在x=0不连续,但|f(x)|=1在x=0处连续.于是应选A. ,φ(x)在x0邻域∪有界
,φ(x)在x0邻域∪有界
 f(x)在x=x0连续.
f(x)在x=x0连续.
 在x=x0既左又右连续,
在x=x0既左又右连续,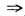 (x)在x=x0连续,因此选B.
(x)在x=x0连续,因此选B. ,则
,则 .
.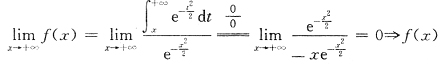 在[0,+∞)有界
在[0,+∞)有界 无界.
无界. ”是f(x)在[a,+∞)无界的
”是f(x)在[a,+∞)无界的 xn∈[a,+∞)使得
xn∈[a,+∞)使得 ,
, ,则f(x)在[a,+∞)无界.若f(x)在[a,+∞)有界,即|f(x)|≤M(x∈[a,+∞))
,则f(x)在[a,+∞)无界.若f(x)在[a,+∞)有界,即|f(x)|≤M(x∈[a,+∞)) |f(xn)|≤M与
|f(xn)|≤M与 矛盾.
矛盾. 对
对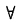 自然数n,f(x)在[n,+∞)无界
自然数n,f(x)在[n,+∞)无界 xn∈[n,+∞),
xn∈[n,+∞), .因此选C.
.因此选C.



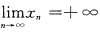 ,对于C.
,对于C.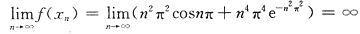 ,
, C中f(x)在[1,+∞)无界.
C中f(x)在[1,+∞)无界.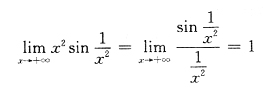
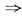 A有界.
A有界.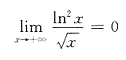
 有界
有界 有界,即B在[1,+∞)有界.
有界,即B在[1,+∞)有界.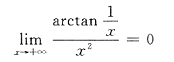
 D在[1,+∞)有界.因此选C.
D在[1,+∞)有界.因此选C. ,f(x)在x=1处可导,则α的取值为
,f(x)在x=1处可导,则α的取值为 (当α+1≥0时该极限不存在).
(当α+1≥0时该极限不存在). 不存在,但
不存在,但 是有界量,又
是有界量,又
 存在,必须
存在,必须 ,此处利用了无穷小量与有界量的乘积是无穷小量.
,此处利用了无穷小量与有界量的乘积是无穷小量.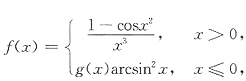 ,其中g(x)是有界函数,则f(x)在x=0处
,其中g(x)是有界函数,则f(x)在x=0处
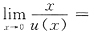

 .因此,曲线y=f(x)在点(x,f(x))的切线在z轴上的截距为
.因此,曲线y=f(x)在点(x,f(x))的切线在z轴上的截距为 ,下求
,下求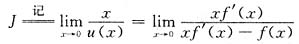



 型极限
型极限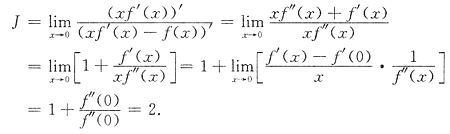


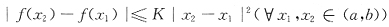 则
则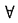 x,x0∈(a,b)有
x,x0∈(a,b)有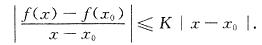
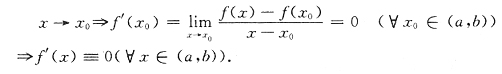 选D.
选D.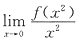 存在是f(x)在x=0可导的
存在是f(x)在x=0可导的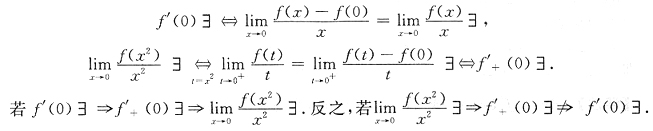 因此选B.
因此选B.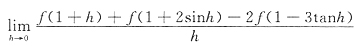 等于
等于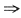 f'(1)=f'(4),我们可由f'(1)可得极限值I.
f'(1)=f'(4),我们可由f'(1)可得极限值I.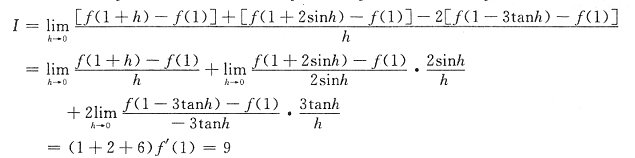
 与Δx是同阶无穷小.
与Δx是同阶无穷小.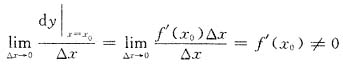
 与Δx是同阶无穷小,①正确.
与Δx是同阶无穷小,①正确. dy=aΔx-Δy.故③不正确.
dy=aΔx-Δy.故③不正确. ,则f'(0)=
,则f'(0)=
 .再由f(x)的连续性
.再由f(x)的连续性 f(0)=0.
f(0)=0.
 当x→x0时是(x-x0)的
当x→x0时是(x-x0)的 .于是,题设可写成
.于是,题设可写成







 ,则
,则 与f'(x)在x=x0处的左右极限
与f'(x)在x=x0处的左右极限 区分开来.
区分开来.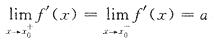 ,只能得出
,只能得出 ,但不能保证f(x)在x0处可导,以及在x=x0处连续和极限存在.
,但不能保证f(x)在x0处可导,以及在x=x0处连续和极限存在. 显然,x≠0时,f'(x)=1因此
显然,x≠0时,f'(x)=1因此

 不存在,因此f(x)在x=0处不连续,不可导.
不存在,因此f(x)在x=0处不连续,不可导. 为大于零的常数,h(x)在x0无定义,
为大于零的常数,h(x)在x0无定义, 均存在,则g(x0)=a,g'-(x0)=b是f(x)在x0可导的
均存在,则g(x0)=a,g'-(x0)=b是f(x)在x0可导的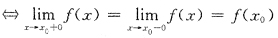
 ,则g(x)在x=x0左连续).
,则g(x)在x=x0左连续).


 .选C.
.选C. f(0)=0.因存在
f(0)=0.因存在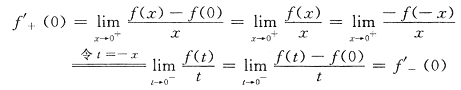
 .选C.
.选C. ,故f'(0)不存在.
,故f'(0)不存在.
 ,在[-a,a]是偶函数,但x=0不是极值点.
,在[-a,a]是偶函数,但x=0不是极值点. 在x=0有垂直于x轴的切线,
在x=0有垂直于x轴的切线, 在x=0不可导.
在x=0不可导.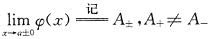 .
.

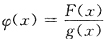 ,由商的求导法则,φ(x)在x=a处可导,这与题设矛盾,所以选A.
,由商的求导法则,φ(x)在x=a处可导,这与题设矛盾,所以选A. 区间上不可导点的个数是
区间上不可导点的个数是 ,只须考察φ(x)不可导点处g(x)是否为零.
,只须考察φ(x)不可导点处g(x)是否为零. 内只有不可导点x=0,
内只有不可导点x=0, ,1,其余均可导.
,1,其余均可导.
 ,g(1)=0.
,g(1)=0. 处不可导,在x=1可导,其余点均可导.因此选B.
处不可导,在x=1可导,其余点均可导.因此选B.
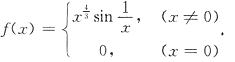

 在x=0不可导.又x→0时,e|x|-1~|x|,arctan|x|~|x|,
在x=0不可导.又x→0时,e|x|-1~|x|,arctan|x|~|x|, .
.


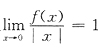 ,则
,则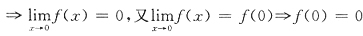 .
.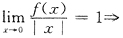
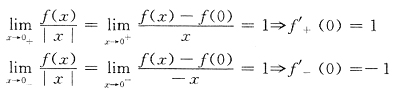





 a,b之值f(x)均可导.关键是x=0处.
a,b之值f(x)均可导.关键是x=0处.
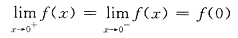



 得
得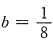 .因此选B.
.因此选B. 可出,则(b,c)=
可出,则(b,c)=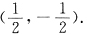




 相切,则常数a=______,b=______.
相切,则常数a=______,b=______. 与
与 的切点为
的切点为 .
. 处的切线方程是
处的切线方程是
 在切点
在切点 处的切线方程是
处的切线方程是
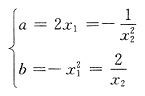

 上任一点P(x,y)处作切线,该切线分别交x轴与y轴于A和B(如下图所示),则
上任一点P(x,y)处作切线,该切线分别交x轴与y轴于A和B(如下图所示),则



 的大小关系与P的位置有关.
的大小关系与P的位置有关. 处的切线方程是
处的切线方程是
 其中(X,Y)为切线上点的坐标,分别令Y=0,X=0得A与B的坐标为(2x,0),
其中(X,Y)为切线上点的坐标,分别令Y=0,X=0得A与B的坐标为(2x,0), ,于是
,于是

