选择题1. 设曲线y=lnx与曲线

在点(x
0,y
0)处有公切线,则常数k与切点分别为
A.

B.

C.
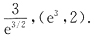
D.
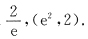
A B C D
D
[解析] 由题设知,(x
0,y
0)同时满足
与

①

②
由②得

,代入①得y
0=lnx
0=2

(x
0,y
0)=(e
2,2),

.
因此选D.
3. 设f(x)在x
0可导,且f'(x
0)>0,则
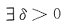
,使得
- A.f(x)在(x0-δ,x+δ)单调上升.
- B.f(x)>f(x0),x∈(x0-δ,x0+δ),x≠x0.
- C.f(x)>f(x0),x∈(x0,x0+δ).
- D.f(x)<f(x0),x∈(x0,x0+δ).
A B C D
C
[解析] 由条件出发,按导数定义

及极限的不等式性质可知,

,当x∈(x
0-δ,x
0+δ),x≠x
0时,
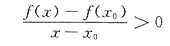

当x∈(x
0,x
0+δ)时f(x)-f(x
0)>0,当x∈(x
0-δ,x
0)时f(x)-f(x
0)<0.
因此选C.
4. 下列函数f(x)中,导函数f'(x)在x=0处不连续的是
A.

B.

C.

D.

A B C D
A
[解析] 关于A,当x≠0时,

而

不存在

f'(x)在x=0不连续.选A.
B,C,D中的三个,f(x)在x=0均连续,
直接求出

类似可证B,C函数f'(x)在x=0连续.因此选A.
5. 设f(x)一阶可导,f(x)>0,f'(x)>0,则当Δx>0时
A.

B.

C.

D.

A B C D
A
[解析] 由积分中值定理

∈(x,x+Δx)使得

(f'(x)>0

f(x)是单调增加的).
因此选A.
由定积分的几何意义来分析,曲线y=f(x)在
x轴上方且单调增加

是曲边梯形ABCD的面积,f(x)Δx是矩形BCDE的面积,因
此

.选A.

6. 设f(x)对一切x∈(-∞,+∞)满足方程(x-1)f"(x)+2(x-1)[f'(x)]
3=1-e
1-x,且f(x)在x-a(a≠1)处f'(a)=0,则x=a
- A.是_f(x)的极小值点.
- B.是f(x)的极大值点.
- C.不是f(x)的极值点.
- D.是f(x)的拐点.
A B C D
A
[解析] 因f'(a)=0于是有(a-1)f"(a)=1-e
1-a。
显然

所以,x=a是极小值点.选A.
8. 函数

的最大值为
A.

B.

C.

D.

A B C D
A
[解析] f(x)为奇函数,f(x)<0(x<0),f(x)>0(x>0).只须在区间[0,+∞)上分析f(x)的单调性.
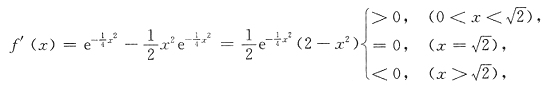

f(x)在[0,+∞)上的最大值为

它也是f(x)在(-∞,+∞)上的最大值.选A.
9. 59设f(x)在[a,+∞)连续,又f(x)在[a,x
0]单调上升,在[x
0,+∞)单调下降,

,则f(x)在[a,+∞)上相应的值域是
- A.[f(a),f(x0)].
- B.[l,f(x0)].
- C.(l,f(x0)].
- D.以上均不对.
A B C D
D
[解析] 由题设y=f(x)有两种可能的图形,由图形可看出f(x)的值域.

f(a)>l时f(x)的值域是(l,f(x
0)] f(a)≤l时f(x)的值域是[f(a),f(x
0)].
因此选D.
因f(x)在[a,x
0]单调上升
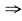
f(a)≤f(x)≤f(x
0)(a≤x≤x
0).
因f(x)在[x
0,+∞)单调下降且

(x
0≤x<+∞).
现设f(a)≤l,则
f(a)≤f(x)≤f(x
0)(x∈[a,+∞))
反之,对

μ∈f(a),f(x
0)],由连续函数介值定理,至少存在一点
x*∈[a,x
0]

[a,+∞),f(x*)=μ.
因此f(x)相应的值域是[f(a),f(x
0)].
当f(a)>l时,则
l<f(x)≤f(x
0)(x∈[a,+∞))
反之,对

μ∈(l,f(x
0)],由于

,

x
1>x
0,f(x
1)<μ
0).
由连续函数介值定理 x*∈(x0,x1)
x*∈(x0,x1)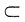 [a,+∞),f(x*)=μ.
[a,+∞),f(x*)=μ.
因此f(x)相应的值域是(l,f(x0)].
综上所述,当f(a)≤l时f(x)的值域是[f(a),f(x0)],当f(a)>l时,f(x)的值域是(l,f(x0)].因此选D.
11. 设f(x)处处可导,则下面命题正确的是
A.若
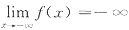
,则必有

B.

,则必有

C.

,则必有

D.

,则必有

A B C D
12. 设f(x)在(0,+∞)二阶可导,满足f(0)=0,f"(x)<0(x>0),又设b>a>0,则a<x<b时恒有
- A.af(x)>xf(a).
- B.bf(x)>xf(b).
- C.xf(x)>bf(b).
- D.xf(x)>af(a).
A B C D
B
[解析] 将A,B分别改写成
A:

,B:

于是,若能证明

或xf(x)的单调性便可选得结论.

令g(x)=xf'(x)-f(x),

g(0)=0,g'(x)=xf"(x)<0(x>0)

g(x)<0(x>0)
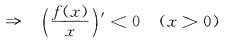

在(0,+∞)单调下降.
当a<x<b时,

.选B.
13. 设f(x)在(1-δ,1+δ)内存在导数,f'(x)单调减少,且f(1)=f'(1)=1,则
- A.在(1-δ,1)和(1,1+δ)内均有f(x)<x.
- B.在(1-δ,1)和(1,1+δ)内均有f(x)>x.
- C.在(1-δ,1)内有f(x)<x,在(1,1+δ)内有f(x)>x.
- D.在(1-δ,1)内有f(x)>x,在(1,1+δ)内有f(x)<x.
A B C D
A
[解析] 为考察f(x)与x之间的关系,设F(x)=f(x)-x,则F'(x)=f'(x)-1,F'(x)在(1-δ,1+δ)单调减少,F'(1)=0,F(1)=0.
当x∈(1-δ,1)时F'(x)>F'(1)=0,因此F(x)在(1-δ,1]内单调递增,F(x)<F(1)=0即在(1-δ,1),F(x)<0.
当x∈(1,1+δ)时,F'(x)<F'(1)=0,因此F(x)在[1,1+δ)内单调递减,F(x)<F(1)=0,即在(1,1+δ)内F(x)<0.因此,选A.
f'(x)在(1-δ,1+δ)严格单调减少

f(x)在(1-δ,1+δ)是凸的

在此区间上,y=f(x)在点(1,f(1))即(1,1)处的切线y-1=f'(1)(x-1)即y=x在此曲线的上方(除切点外).因此
f(x)<x(x∈(1-δ,1+δ),x≠1)
15. 设

,则
- A.x=0是f(x)的极值点,但(0,1)不是曲线y=f(x)的拐点.
- B.x=0不是f(x)的极值点,但(0,1)是曲线y=f(x)的拐点.
- C.x=0是f(x)的极值点,且(0,1)是曲线y=f(x)的拐点.
- D.x=0不是f(x)的极值点,(0,1)也不是曲线y=f(x)的拐点.
A B C D
C
[解析] 显然f(x)在(-∞,+∞)连续.只须考祭f在x=0某空心邻域如

,x≠0时f'(x)与f"(x)的变化.

由此可得x=0是f(x)的极值点,且(0,1)是曲线y=f(x)的拐点.因此选C.
由y=cosx,

的图形可得y=f(x)的图形.

因此选C.
16. 设f(x)具有二阶连续导数,且

,则
- A.f(1)是f(x)的极大值.
- B.f(1)是f(x)的极小值.
- C.(1,f(1))是曲线f(x)的拐点坐标.
- D.f(1)不是f(x)的极值,(1,f(1))也不是曲线f(x)的拐点坐标.
A B C D
B
[解析] 因

,由极限的保号性质,存在δ>0,当0<|x-1|<δ时

,又因(x-1)
2>0(x≠1),所以当0<|x-1|<δ时,f"(x)>0,因此f'(x)在(1-δ,1+δ)单调递增,从而当1-δ<x<1,f'(x)<f'(1)=0,当1<x<1+δ,f'(x)>f'(1)=0,由取得极值的充分条件,f(1)是f(x)的极小值.因此选B.
特殊选取f(x)满足:

.
取

,则f(x)满足题中条件,f(x)在x=1处取极小值,而其余均不正确.因此选B.
17. 设f(x)在(-∞,+∞)可导,x
0≠0,(x
0,f(x
0))是y=f(x)的拐点,则
A.x
0必是f'(x)的驻点.
B.(-x
0,-f(x
0))必是y=-f(-x)的拐点.
C.(-x
0,-f(-x
0))必是y=-f(x)的拐点.
D.对
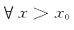
与x<x
0,y=f(x)的凹凸性相反.
A B C D
B
[解析] ](x
0,f(x
0))是y=f(x)的拐点,f"(x
0)不一定存在,所以不选A.拐点是函数的局部性质,(x
0,f(x
0))是y=f(x)的拐点,只能保证在x
0的一个邻域内,y=f(x)的凹凸性相反,所以不选D.曲线y=-f(x)与y=f(x)关于x轴对称,(x
0,f(x
0))是y=f(x)的拐点,不能保证(-x
0,-f(-x
0))是y=f(x)的拐点.例如y=f(x)=(x-1)
3,只有拐点(1,0),但(-1,-f(-1))不是y=-f(x)=-(x-1)
3的拐点.所以不选C.因此选B.
从几何上分析也很简单,y=f(x)与y=-f(-x)的图形关于原点对称.x
0≠0,(x
0,f(x
0))是y=f(x)的拐点

是y=-f(-x)的拐点.因此选B.
18. 设函数f(x)在(-∞,+∞)上有定义,则下述命题中正确的是
A.若f(x)在(-∞,+∞)上可导且单调增加,则对一切x∈(-∞,+∞),都有f'(x)>0.
B.若f(x)在点x
0处取得极值,则f'(x
0)=0.
C.若f"(x
0)=0,则(x
0,f(x
0))是曲线y=f(x)的拐点坐标.
D.若f'(x
0)=0,f"(x
0)=0,
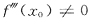
,则x
0一定不是f(x)的极值点.
A B C D
D
[解析] 若在(-∞,+∞)上f'(x)>0,则一定有f(x)在(-∞,+∞)上单调增加,但可导函数f(x)在(-∞,+∞)单调增加,只能有f'(x)≥0(即可能在某些点上f'(x)=0).例如f(x)=x
3在(-∞,+∞)上单调增加,f'(0)=0.因此不选A.
f(x)若在x
0处取得极值,且f'(x
0)存在,则有f'(x
0)=0,但当f(x)在x
0处取得极值,在x
0处不可导,就得不到f'(x
0)=0,例如f(x)=|x|在x
0=0处取得极小值,它在x
0=0处不可导,因此不选B.
如果f(x)在x
0处二阶导数存在,且(x
0,f(x
0))是曲线的拐点坐标,则f"(x
0)=0,反之不一定,例如f(x)=x
4在x
0=0处f"(0)=0,但f(x)在(-∞,+∞)没有拐点,因此不选C.由上分析,应选D.
可以证明D是正确的.
不妨设

.由带皮亚诺余项的泰勒公式得

当x→x
0时o(1)为无穷小量.由极限的保号性质

,当0<|x-x
0|<δ时,
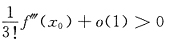

时f(x)-f(x
0)<0,x
0<x<x
0+δ时f(x)-f(x
0)>0.
因此f(x
0)不是f(x)的极值.
19. 设f(x)在[a,b]可导,又

,则
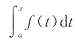
在(a,b)内
A B C D
C
[解析] 考察

,则F(a)-F(b)=0,且所给条件用F(x)表示即
F"(x)+(F'(x))
2-F(x)=0. (*)
若F(x)在(a,b)恒正,则F(x)在(a,b)取正最大值即

,x
0∈(a,b).由极大值点的性质

,F"(x
0)≤0.
但由(*)式得F"(x
0)=F(x
0)>0,这便矛盾.
若F(x)在(a,b)恒负,则

,于是同样得矛盾.
因此,A,B不对,同样D也不对.选C.
20. 设f(x),g(x)在(-∞,+∞)可导且

又a<b,f(a)=f(b)=0,则g(x)在[a,b]
- A.恒正.
- B.恒负.
- C.至少有一个零点.
- D.单调.
A B C D
C
[解析] 考察

若g(x)在[a,b]无零点
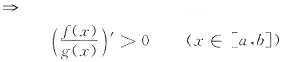

在[a,b]单调上升,与

矛盾.
因此g(x)在[a,b]至少有一个零点.应选C.
21. 函数y=f(x)在(-∞,+∞)连续,其二阶导函数的图形如下图所示,则y=f(x)的拐点的个数是

A B C D
C
[解析] 只须考察f"(x)=0的点与f"(x)不存在的点.
f"(x
1)=f"(x
4)=0,在x=x
1,x
4两侧f"(x)变号,故凹凸性相反,
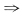
(x
1,f(x
1)),(x
4,f(x
4))是y=f(x)的拐点.
x=0处f"(0)不存在,但f(x)在x=0连续,在x=0两侧f"(x)变号,因此(0,f(0))也是y=f(x)的拐点.
虽然f"(x
3)=0,但在x=x
3。两侧f"(x)>0,y=f(x)是凹的.(x
3,f(x
3))不是y=f(x)的拐点.
因此总共有3个拐点.选C.
22. 设[0,+∞)区间上y=f(x)的导函数的图形如下图所示

则y=f(x)的拐点的个数是
A B C D
C
[解析] 只须考察f"(x)=0的点,这里就是f'(x)的驻点,即x=x
1,x
3,x
5,与f"(x)不
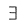
的点,这就是f'(x)的尖点x
4.
在x=x
1,x
6两侧f'(x)的单调性相反,故凹凸性相反,
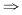
(x
1,f(x
1)),(x
6,f(x
6))是y=f(x)的拐点,在x=x
3处,虽f"(x
3)=0,但x=x
3两侧f'(x)均单调上升即x=x
3两侧y=f(x)均是凹的,(x
3,f(x
3))不是y=f(x)的拐点.虽然f"(x
4)不

,但f(x)在x=x
4连续,在x=x
4两侧f'(x)的单调性相反,故凹凸性相反,(x
4,f(x
4))也是y=f(x)的拐点.因此共有三个拐点.选C.
24. 设f(x)=x
3=3x
2-9x-8,则f(x)在(-∞,+∞)零点个数为
A B C D
A
[解析] (1)考察f(x)的单调性区间.
f'(x)=3x
2-6x-9
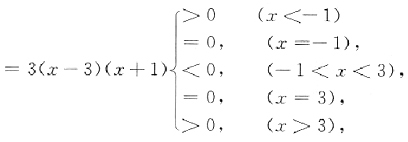

在(-∞,-1],[3,+∞)单调上升,在[-1,3]单调下降.
(2)极值点处函数值符号f(-1)=-3<0,f(3)<0
(3)边界处极限值.

.
综上分析,y=f(x)的图形如下图所示.当x∈(-∞,3]时f(x)<0,f(x)无零点.

当x∈[3,+∞)时f(x)单调上升,f(3)与

异号.

f(x)在(3,+∞)存在唯一零点

在(-∞,+∞)存在唯一零点.选A.
26. 函数f(x)在[1,2]有二阶导数,f(2)=0,F(x)=(x-1)
2f(x),则F"(x)在(1,2)上
- A.没有零点.
- B.必有零点.
- C.若有零点,必不止一个.
- D.若有零点必唯一.
A B C D
B
[解析] F(x)在[1,2]上连续,(1,2)内可导且F(1)=F(2),由罗尔定理,至少存在一点x
0∈(1,2]使F'(x
0)=0,又F'(x)=2(x-1)f(x)+(x-1)
2f'(x)

F'(x
0)=F'(1)

F'(x)在[1,x
0]上满足罗尔定理条件,所以,至少存在ξ(1,x
0)

(1,2)上使
F"(ξ)=0.因此选B.
由题设,无法判断F'(x)的单调性,也无法判定除x
0,x=1以外F'(x)是否还有零点,因此不选C和D.
27. 设f(x)=ax
3-6ax
2+b在区间[-1,2]上的最大值是3,最小值是-29,且a>0,则
- A.a=2,b=-29.
- B.a=3,b=2.
- C.a=2,b=3.
- D.以上都不对.
A B C D
C
[解析] 令f'(x)=3ax
2-12ax=3ax(x-4)=0得x
1=0,x
2=4(不合题意舍去)
f(0)=b,f(-1)=-7a+b,f(2)=-16a+b,由于a>0;所以,f(0)是最大值,f(2)是最小值.

所以选C.
28. 曲线
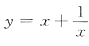
的点与单位圆x
2+y
2=1的点之间的最短距离为d,则
A.d=1.
B.

C.0<d<1.
D.

A B C D
B
[解析] 由对称性只须考察x>0,y>0的情形.因为任意给定曲线

上点M(x,y),它到单位圆周x
2+y
2=1的最短距离点是OM连线Ngat_立圆周的交点(见下图)单位圆x
2+y
2=1上各点到原点距离为1,所以只需考察曲线

上点M(x,y)到原点的距离的平方

的最小值即可.

令t=x
2,
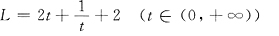


L的最小值是

于是

29. 设f(x)在[a,b]上有定义,在(a,b)内可导,则
A.当f(a)·f(b)<0时,

使f(ξ)=0.
B.对

,有

C.当f(a)=f(b)时
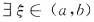
,使f'(ξ)=0.
D.

,使f(b)-f(a)=f'(ξ)(b-a).
A B C D
B
[解析] 我们已经知道,若f(x)在[a,b]连续,在(a,b)可导,则A、C、D均正确.这里只有f(x)在(a,b)可导,没假设在[a,b]连续,不能保证A,C,D正确.
例如,由

可知A不正确.
由

知C,D均不正确.
因此选B.
对

,f(x)在ξ点可导
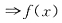
在ξ点连续

选B.
30. 设f(x)=xsinx+cosx,下列命题中正确的是
A.f(0)是极大值,

是极小值.
B.f(0)是极小值,

是极大值.
C.f(0),

均是极大值.
D.f(0),

均是极小值.
A B C D
B
[解析] 用极值的第一充分判别法
f'(x)=xcosx+sinx-sinx=xcosx
取δ>0充分小.

选B.
用极值的第二充分判别法.
f'(x)=xcosx,f"(x)=cosx-xsinx
f'(0)=0,f"(0)=1>0

f(0)为极小值.
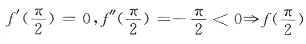
为极大值.选B.
31. 函数

- A.单调上升.
- B.单调下降.
- C.为常数.
- D.有两个单调性区间.
A B C D
C
[解析] 归结为求f'(x).
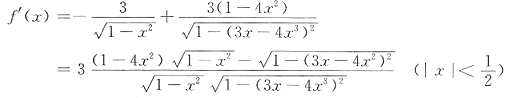
考察f'(x)的分子:
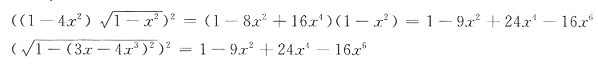

,又f(x)(初等函数)在定义域
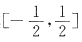
连续.

在

为常数.
选C.
32. 曲线

的斜渐近线为
A.

B.
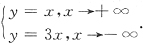
C.
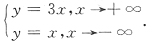
D.

A B C D
B
[解析]

x→+∞时的斜渐近线为y=x

x→-∞时的斜渐近线为y=3x.选B.
33. 设f(x)在[a,b]连续,在(a,b)二阶可导,又f(a)=f(b),f'(x)在[a,b)连续,f'+(a)<0,则
A.

B.

C.

D.

A B C D
C
[解析] 由罗尔定理

,f'(ξ
0)=0.现对f'(x)在[a,ξ
0]上用拉格朗日中值定理

,

因此选C.
特取f(x)=-x(1-x)=-x+x
3(x∈[0,1])

,f(0)=-1<0,f(0)=f(1)=0.f"(x)=2,f(x)<0=f(0)(x∈(0,1))
因此,A、B、D不对,选C.
34. 设f(x)在[0,+∞)上可导且有n个不同的零点:0<x
1<x
2<…<x
n,则f(x)+f'(x)在[0,+∞)内正确的性质是
- A.至少有n个零点.
- B.至少有n-1个零点.
- C.恰有n个零点.
- D.至多有n个零点.
A B C D
B
[解析] 注意f(x)+f'(x)与e
x(f(x)+f'(x))=(e
xf(x))'有相同的零点.
f(x)在[0,+∞)可导且有n个不同的零点

在[0,+∞)可导且有n个不同的零点.
由罗尔定理知,e
xf(x)的两个零点之间一定有(e
xf(x))'的一个零点.因此(e
xf(x))'至少有n-1个零点,即e
x(f(x)+f'(x))也就是f(x)+f'(x)至少有n-1个零点.
选B.
35. 设f(x)在[a,b]连续,在(a,b)二阶可导,又f(a)=f(b),f"(x)≠0(x∈(a,b)),则下列结论成立的是
A.在(a,b)内f'(x)≠0.
B.

C.

D.

A B C D
C
[解析] 由罗尔定理知,

,f'(ξ)=0.又f"(x)≠0(x∈(a,b))

f"(x)在(a,b)恒正或恒负

在(a,b)单调,

在(a,b)的零点是唯一的.选C.
36. 以下四个命题中,正确的是
- A.若f'(x)在(0,1)内连续,则f(x)在(0,1)内有界.
- B.若f(x)在(0,1)内连续,则f(x)在(0,1)内有界.
- C.若f'(x)在(0,1)内有界,则f(x)在(0,1)内有界.
- D.若f(x)在(0,1)内有界,则f'(x)在(0,1)内有界.
A B C D
C
[解析] 举例否定错误的命题.
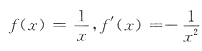
,它们在(0,1)均连续且无界.A,B不正确.

在(0,1)有界,但

在(0,1)无界.D不正确.应选C.
联系f'(x)与f(x)的是拉格朗日中值定理.取定x
0∈(0,1),则由拉格朗日中值定理知,对

在x与x
0之间使得
f(x)-f(x
0)=f'(ξ)(x-x
0)
于是
|f(x)|≤|f(x
0)|+|f'(ξ)||x-x
0|≤|f(x
0)|+M(x∈(0,1))
其中|f"(x)|≤M(x∈(0,1)).因此f(x)在(0,1)有界.选C.
37. 设f(x)在(a,+∞)可导,则f'(x)在(a,+∞)有界是f(x)在(a,+∞)有界的
- A.必要非充分条件.
- B.充分非必要条件.
- C.充分且必要条件.
- D.既非充分也非必要条件.
A B C D
D
[解析] 设f(x)=x,则f'(x)=1在(a,∞)有界,但f(x)在(a,+∞)无界.
设f(x)=sinx
2,则f(x)在(a,+∞)有界,但f'(x)=2xcosx
2在(a,+∞)无界

时

。
因此选D.
38. 设f(x)在[a,b]连续,在(a,b)内有二阶导数,且f(a)=f(b)=0,f(c)>0,其中a<c<b,则以下命题正确的是
A.至少

一点ξ∈(a,b),使得f"(ξ)>0.
B.至少

一点ξ∈(a,b),使得f"(ξ)=0.
C.至少

一点ξ∈(a,b),使得f"(ξ)<0.
D.对

A B C D
C
[解析] 分别在[a,c],[c,b]上用拉格朗日中值定理,

,ξ
2∈(c,b)使得

在[ξ
1,ξ
2]上再对f'(x)用拉格朗日中值定理
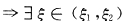
使得
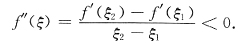
即C成立.选C.
取f(x)=x(1-x),x∈[0,1]

f(0)=f(1)=0,f(x)>0(x∈(0,1)),f"(x)=-2.由此知A,B不正确.若取f(x)如图所示,则知D不对.因此,选C.

39. 设f(x)在(a,b)可导,x
0∈(a,b)是f'(x)的间断点,则该间断点一定是
A.可去间断点. B.跳跃间断点.
C.无穷型间断点. D.非无穷型第二类间断点.
注:若

中有一个为∞,称x
0是g(x)的无穷型间断点.
A B C D
D
[解析] 判断f'(x)的间断点x
0的类型就要考察

若

均存在
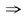

由于
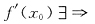
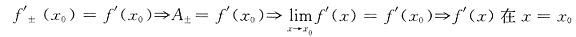
连续,与已知矛盾.

A,B不正确.
若

,与

矛盾.同理,若

,与

矛盾.因此C不正确.选D.
40. 设f(x)在x=0四阶可导,且在x=0某邻域

在x=0连续,则必有f
(4)(0)=
A B C D
C
[解析] 由题设,即

即

即

与f(x)在x=0的四阶麦克劳林公式

相比较得
f(0)=f'(0)=f
(2)(0)=f
(3)(0)=0
f
(4)(0)=2·4!=48.选C.
41. 考察下列叙述:
①设f
2(x)在x=x
0连续,则f(x)在x=x
0连续.
②设f(x)在x=x
0连续,则|f(x)|在x=x
0连续.
③设|f(x)|在[a,b]可积,则f(x)在[a,b]可积.
④设f(x)在[a,b]有界,只有有限个间断点,则|f(x)|在[a,b]可积,即在[a,b]存在定积分.
我们可知
- A.只有①,②正确.
- B.只有②,③正确.
- C.只有②,④正确.
- D.只有③,④正确.
A B C D
C
[解析] 由题目的设置可知,这四个命题中有两个是正确的,两个是错误的.
由“

,则

”可得“若

,则

”,因此,若f(x)在x=x
0连续,则|f(x)|在x=x
0连续,即②正确.
由f(x)在[a,b]有界,只有有限个间断点,则|f(x)|在[a,b]也有界,也只有有限个间断点(因f(x)的连续点必是|f(x)|的连续点),因而|f(x)|在[a,b]可积即④正确.选C.
①是不正确的,例如,

在x=0间断,但f
2(x)=1在x=0。连续.③也是错的,例如
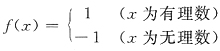
,则

不存在(易构造两个积分和有不同的极限),但|f(x)|=1在[a,b]可积.因此,只能是②,④正确,选C.
42. 下列函数在指定区间上不存在定积分的是
A.

B.

C.
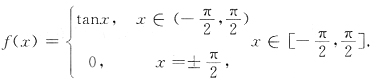
D.

A B C D
C
[解析] f(x)在[a,b]
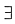
定积分的必要条件是f(x)在[a,b]有界.因此,若f(x)在[a,b]无界,则f(x)在[a,b]不

定积分.
函数C在

无界

在

不

定积分.选C.
f(x)在[a,b]可积的充分条件是:f(x)在[a,b]有界,至多有有限个间断点.

A,B,D函数在指定区间可积.因此选C.
44.

A.π.
B.

C.
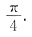
D.

A B C D
B
[解析] 分母先配方后再作平移变换

选B.
先改写成

选B.
[分析3]令x=sin
2t,则

选B.
45. 在下列定积分中,积分值等于零的是
A.

B.

C.

D.

A B C D
C
[解析] A项x
7sin
9x是偶函数

B项

为奇函数
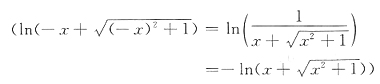

为偶函数

选C.
分析C

选C.
46. 下列用牛顿—莱布尼兹公式计算定积分的作法中,错误的作法一共有
(1)

(2)

(3)

(4)

A B C D
D
[解析] 必须逐一分析
(1)
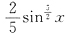
仅在

上是被积函数的原函数,在

上的原函数是

.因此这里的作法是错误的.
(2)

在x=0无定义,在[-1,1]上无界,不存在定积分,这里错误地应用了牛顿—莱布尼兹公式.
(3)

不是整个区间[0,π]上的原函数,它在

无定义,只是

与

上的原函数,不能在[0,π]上用牛顿—莱布尼兹公式.
(4)

在x=0无定义,可任意补充定义f(0)后,

仍不是f(x)在整个区间[-1,1]上的原函数,因为它在x=0无定义,因此不能在[-1,1]上用牛顿—莱布尼兹公式.
因此选D.
47. 下列结论正确的是
A.

B.

C.

D.

A B C D
A
[解析]
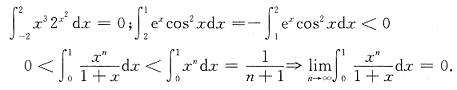
因此,B、C、D不正确.选A.

48.

A.

B.

C.

D.

A B C D
A
[解析]

,被积函数以π为周期,由周期函数的积分性质
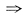

因此选A.
49. 设F(x)是f(x)在(a,b)上的一个原函数,则f(x)+F(x)在(a,b)上
- A.可导.
- B.连续.
- C.存在原函数.
- D.是初等函数.
A B C D
C
[解析] 因F(x)是f(x)在(a,b)上的一个原函数,所以F'(x)=f(x),因此F(x)在(a,b)上连续,于是F(x)在(a,b)上存在原函数,从而f(x)+F(x)在(a,b)上存在原函数.因此选C.
函数f(x)在(a,b)上存在原函数,f(x)在(a,b)上不连续,例如
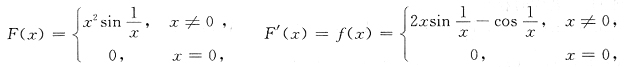
显然f(x)在x=0处不连续.函数f(x)在(a,b)上存在原函数,又因F(x)在(a,b)上连续,因此F(x)+f(x)在(a,b)不连续,所以不选B从而也不选A.
f(x)+F(x)不一定是初等函数,例如f(x)=e
x2在(-∞,+∞)上存在一个原函

数F(x),它不是初等函数

F(z)+f(x)不是初等函数,因此不选D.
50. 设

则在区间(-1,1)上
- A.f(x)与g(x)都存在原函数.
- B.f(x)与g(x)都不存在原函数.
- C.f(x)存在原函数,g(x)不存在原函数.
- D.f(x)不存在原函数,g(x)存在原函数.
A B C D
D
[解析] 这是讨论原函数的存在性问题.我们知道,若F(x)在(a,b)连续,则F(x)在(a,b)一定存在原函数,这里g(x)在(-1,1)连续,所以g(x)在(-1,1)存在原函数.
余下的是f(x)在(-1,1)是否存在原函数(x=0是f(x)的间断点).
方法1 f(x)在[0,1)的原函数为

,在(-1,0)的原函数为sinx+C
2,在x=0处该原函数必连续:
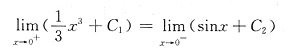

C
1=C
2.若f(x)在(-1,1)存在原函数则应是

但此F(x)在x=0不可导,因为

因此f(x)在(-1,1)不存在原函数.选D.
方法2 因x=0是f(x)的第一类间断点,所以f(x)在(-1,1)有第一类间断点,

f(x)在(-1,1)不存在原函数.选D.
 在点(x0,y0)处有公切线,则常数k与切点分别为
在点(x0,y0)处有公切线,则常数k与切点分别为

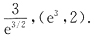
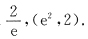
 ①
① ②
② ,代入①得y0=lnx0=2
,代入①得y0=lnx0=2 (x0,y0)=(e2,2),
(x0,y0)=(e2,2), .
.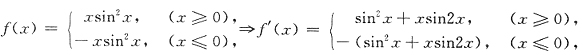
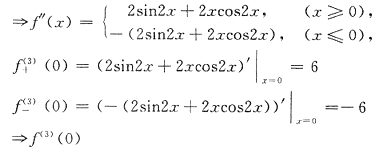 不存在.因此n=2.选C.
不存在.因此n=2.选C.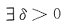 ,使得
,使得
 ,当x∈(x0-δ,x0+δ),x≠x0时,
,当x∈(x0-δ,x0+δ),x≠x0时,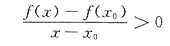
 当x∈(x0,x0+δ)时f(x)-f(x0)>0,当x∈(x0-δ,x0)时f(x)-f(x0)<0.
当x∈(x0,x0+δ)时f(x)-f(x0)>0,当x∈(x0-δ,x0)时f(x)-f(x0)<0.




 不存在
不存在 f'(x)在x=0不连续.选A.
f'(x)在x=0不连续.选A.




 ∈(x,x+Δx)使得
∈(x,x+Δx)使得
 f(x)是单调增加的).
f(x)是单调增加的). 是曲边梯形ABCD的面积,f(x)Δx是矩形BCDE的面积,因
是曲边梯形ABCD的面积,f(x)Δx是矩形BCDE的面积,因 .选A.
.选A.
 所以,x=a是极小值点.选A.
所以,x=a是极小值点.选A.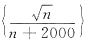 中的最大项n为
中的最大项n为 ,x≥1,求f(x)在[1,+∞)上的最大值点:
,x≥1,求f(x)在[1,+∞)上的最大值点: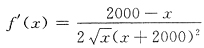 ,令f'(x)=0,得x=2000,当1≤x<2000时,f'(x)>0,f(x)↗,当x>2000时f'(x)<0,f(x)↘,因此在x=2000是f(x)的最大值点.n=2000是该数列的最大项.选D.
,令f'(x)=0,得x=2000,当1≤x<2000时,f'(x)>0,f(x)↗,当x>2000时f'(x)<0,f(x)↘,因此在x=2000是f(x)的最大值点.n=2000是该数列的最大项.选D. 的最大值为
的最大值为



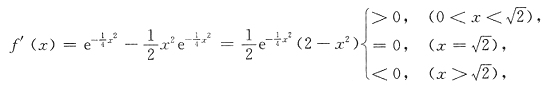
 f(x)在[0,+∞)上的最大值为
f(x)在[0,+∞)上的最大值为
 ,则f(x)在[a,+∞)上相应的值域是
,则f(x)在[a,+∞)上相应的值域是
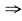 f(a)≤f(x)≤f(x0)(a≤x≤x0).
f(a)≤f(x)≤f(x0)(a≤x≤x0). (x0≤x<+∞).
(x0≤x<+∞). μ∈f(a),f(x0)],由连续函数介值定理,至少存在一点
μ∈f(a),f(x0)],由连续函数介值定理,至少存在一点 [a,+∞),f(x*)=μ.
[a,+∞),f(x*)=μ. μ∈(l,f(x0)],由于
μ∈(l,f(x0)],由于 ,
, x1>x0,f(x1)<μ
x1>x0,f(x1)<μ x*∈(x0,x1)
x*∈(x0,x1)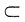 [a,+∞),f(x*)=μ.
[a,+∞),f(x*)=μ.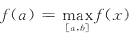 ,则
,则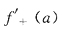
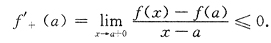 选D.
选D. 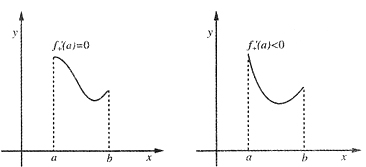
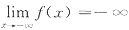 ,则必有
,则必有
 ,则必有
,则必有
 ,则必有
,则必有
 ,则必有
,则必有
 ,B:
,B:
 或xf(x)的单调性便可选得结论.
或xf(x)的单调性便可选得结论.
 g(0)=0,g'(x)=xf"(x)<0(x>0)
g(0)=0,g'(x)=xf"(x)<0(x>0) g(x)<0(x>0)
g(x)<0(x>0)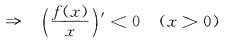
 在(0,+∞)单调下降.
在(0,+∞)单调下降. .选B.
.选B. f(x)在(1-δ,1+δ)是凸的
f(x)在(1-δ,1+δ)是凸的 在此区间上,y=f(x)在点(1,f(1))即(1,1)处的切线y-1=f'(1)(x-1)即y=x在此曲线的上方(除切点外).因此
在此区间上,y=f(x)在点(1,f(1))即(1,1)处的切线y-1=f'(1)(x-1)即y=x在此曲线的上方(除切点外).因此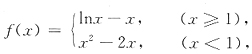 则
则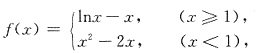
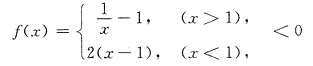
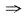 f(x)在(-∞,+∞)单调下降.
f(x)在(-∞,+∞)单调下降.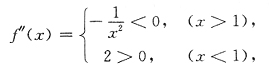
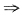 (1,f(1))是y=f(x)的拐点.选C.
(1,f(1))是y=f(x)的拐点.选C. ,则
,则 ,x≠0时f'(x)与f"(x)的变化.
,x≠0时f'(x)与f"(x)的变化.
 的图形可得y=f(x)的图形.
的图形可得y=f(x)的图形.
 ,则
,则 ,由极限的保号性质,存在δ>0,当0<|x-1|<δ时
,由极限的保号性质,存在δ>0,当0<|x-1|<δ时 ,又因(x-1)2>0(x≠1),所以当0<|x-1|<δ时,f"(x)>0,因此f'(x)在(1-δ,1+δ)单调递增,从而当1-δ<x<1,f'(x)<f'(1)=0,当1<x<1+δ,f'(x)>f'(1)=0,由取得极值的充分条件,f(1)是f(x)的极小值.因此选B.
,又因(x-1)2>0(x≠1),所以当0<|x-1|<δ时,f"(x)>0,因此f'(x)在(1-δ,1+δ)单调递增,从而当1-δ<x<1,f'(x)<f'(1)=0,当1<x<1+δ,f'(x)>f'(1)=0,由取得极值的充分条件,f(1)是f(x)的极小值.因此选B. .
. ,则f(x)满足题中条件,f(x)在x=1处取极小值,而其余均不正确.因此选B.
,则f(x)满足题中条件,f(x)在x=1处取极小值,而其余均不正确.因此选B.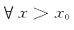 与x<x0,y=f(x)的凹凸性相反.
与x<x0,y=f(x)的凹凸性相反. 是y=-f(-x)的拐点.因此选B.
是y=-f(-x)的拐点.因此选B.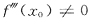 ,则x0一定不是f(x)的极值点.
,则x0一定不是f(x)的极值点. .由带皮亚诺余项的泰勒公式得
.由带皮亚诺余项的泰勒公式得
 ,当0<|x-x0|<δ时,
,当0<|x-x0|<δ时,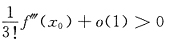
 时f(x)-f(x0)<0,x0<x<x0+δ时f(x)-f(x0)>0.
时f(x)-f(x0)<0,x0<x<x0+δ时f(x)-f(x0)>0. ,则
,则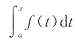 在(a,b)内
在(a,b)内 ,则F(a)-F(b)=0,且所给条件用F(x)表示即
,则F(a)-F(b)=0,且所给条件用F(x)表示即 ,x0∈(a,b).由极大值点的性质
,x0∈(a,b).由极大值点的性质 ,F"(x0)≤0.
,F"(x0)≤0. ,于是同样得矛盾.
,于是同样得矛盾.


 在[a,b]单调上升,与
在[a,b]单调上升,与 矛盾.
矛盾.
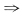 (x1,f(x1)),(x4,f(x4))是y=f(x)的拐点.
(x1,f(x1)),(x4,f(x4))是y=f(x)的拐点.
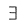 的点,这就是f'(x)的尖点x4.
的点,这就是f'(x)的尖点x4. (x1,f(x1)),(x6,f(x6))是y=f(x)的拐点,在x=x3处,虽f"(x3)=0,但x=x3两侧f'(x)均单调上升即x=x3两侧y=f(x)均是凹的,(x3,f(x3))不是y=f(x)的拐点.虽然f"(x4)不
(x1,f(x1)),(x6,f(x6))是y=f(x)的拐点,在x=x3处,虽f"(x3)=0,但x=x3两侧f'(x)均单调上升即x=x3两侧y=f(x)均是凹的,(x3,f(x3))不是y=f(x)的拐点.虽然f"(x4)不 ,但f(x)在x=x4连续,在x=x4两侧f'(x)的单调性相反,故凹凸性相反,(x4,f(x4))也是y=f(x)的拐点.因此共有三个拐点.选C.
,但f(x)在x=x4连续,在x=x4两侧f'(x)的单调性相反,故凹凸性相反,(x4,f(x4))也是y=f(x)的拐点.因此共有三个拐点.选C.
 ,所以,x=0为曲线的垂直渐近线,
,所以,x=0为曲线的垂直渐近线,
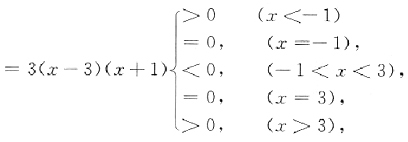
 在(-∞,-1],[3,+∞)单调上升,在[-1,3]单调下降.
在(-∞,-1],[3,+∞)单调上升,在[-1,3]单调下降. .
.
 异号.
异号. f(x)在(3,+∞)存在唯一零点
f(x)在(3,+∞)存在唯一零点 在(-∞,+∞)存在唯一零点.选A.
在(-∞,+∞)存在唯一零点.选A. F'(x0)=F'(1)
F'(x0)=F'(1) F'(x)在[1,x0]上满足罗尔定理条件,所以,至少存在ξ(1,x0)
F'(x)在[1,x0]上满足罗尔定理条件,所以,至少存在ξ(1,x0) (1,2)上使
(1,2)上使
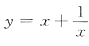 的点与单位圆x2+y2=1的点之间的最短距离为d,则
的点与单位圆x2+y2=1的点之间的最短距离为d,则

 上点M(x,y),它到单位圆周x2+y2=1的最短距离点是OM连线Ngat_立圆周的交点(见下图)单位圆x2+y2=1上各点到原点距离为1,所以只需考察曲线
上点M(x,y),它到单位圆周x2+y2=1的最短距离点是OM连线Ngat_立圆周的交点(见下图)单位圆x2+y2=1上各点到原点距离为1,所以只需考察曲线 上点M(x,y)到原点的距离的平方
上点M(x,y)到原点的距离的平方 的最小值即可.
的最小值即可.
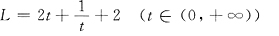

 L的最小值是
L的最小值是

 使f(ξ)=0.
使f(ξ)=0. ,有
,有
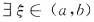 ,使f'(ξ)=0.
,使f'(ξ)=0. ,使f(b)-f(a)=f'(ξ)(b-a).
,使f(b)-f(a)=f'(ξ)(b-a). 可知A不正确.
可知A不正确. 知C,D均不正确.
知C,D均不正确. ,f(x)在ξ点可导
,f(x)在ξ点可导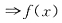 在ξ点连续
在ξ点连续 选B.
选B. 是极小值.
是极小值. 是极大值.
是极大值. 均是极大值.
均是极大值. 均是极小值.
均是极小值.
 f(0)为极小值.
f(0)为极小值.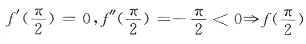 为极大值.选B.
为极大值.选B.
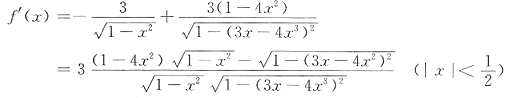
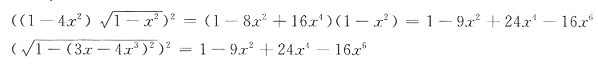
 ,又f(x)(初等函数)在定义域
,又f(x)(初等函数)在定义域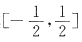 连续.
连续. 在
在 为常数.
为常数. 的斜渐近线为
的斜渐近线为
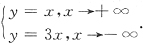
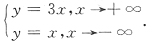







 ,f'(ξ0)=0.现对f'(x)在[a,ξ0]上用拉格朗日中值定理
,f'(ξ0)=0.现对f'(x)在[a,ξ0]上用拉格朗日中值定理 ,
,
 ,f(0)=-1<0,f(0)=f(1)=0.f"(x)=2,f(x)<0=f(0)(x∈(0,1))
,f(0)=-1<0,f(0)=f(1)=0.f"(x)=2,f(x)<0=f(0)(x∈(0,1)) 在[0,+∞)可导且有n个不同的零点.
在[0,+∞)可导且有n个不同的零点.


 ,f'(ξ)=0.又f"(x)≠0(x∈(a,b))
,f'(ξ)=0.又f"(x)≠0(x∈(a,b)) f"(x)在(a,b)恒正或恒负
f"(x)在(a,b)恒正或恒负 在(a,b)单调,
在(a,b)单调, 在(a,b)的零点是唯一的.选C.
在(a,b)的零点是唯一的.选C.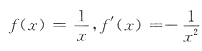 ,它们在(0,1)均连续且无界.A,B不正确.
,它们在(0,1)均连续且无界.A,B不正确. 在(0,1)有界,但
在(0,1)有界,但 在(0,1)无界.D不正确.应选C.
在(0,1)无界.D不正确.应选C. 在x与x0之间使得
在x与x0之间使得 时
时 。
。 一点ξ∈(a,b),使得f"(ξ)>0.
一点ξ∈(a,b),使得f"(ξ)>0. 一点ξ∈(a,b),使得f"(ξ)=0.
一点ξ∈(a,b),使得f"(ξ)=0. 一点ξ∈(a,b),使得f"(ξ)<0.
一点ξ∈(a,b),使得f"(ξ)<0.
 ,ξ2∈(c,b)使得
,ξ2∈(c,b)使得
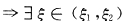 使得
使得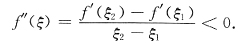
 f(0)=f(1)=0,f(x)>0(x∈(0,1)),f"(x)=-2.由此知A,B不正确.若取f(x)如图所示,则知D不对.因此,选C.
f(0)=f(1)=0,f(x)>0(x∈(0,1)),f"(x)=-2.由此知A,B不正确.若取f(x)如图所示,则知D不对.因此,选C.
 中有一个为∞,称x0是g(x)的无穷型间断点.
中有一个为∞,称x0是g(x)的无穷型间断点. 若
若 均存在
均存在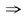

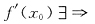
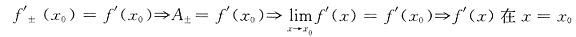 连续,与已知矛盾.
连续,与已知矛盾. A,B不正确.
A,B不正确. ,与
,与 矛盾.同理,若
矛盾.同理,若 ,与
,与 矛盾.因此C不正确.选D.
矛盾.因此C不正确.选D.




 ,则
,则 ”可得“若
”可得“若 ,则
,则 ”,因此,若f(x)在x=x0连续,则|f(x)|在x=x0连续,即②正确.
”,因此,若f(x)在x=x0连续,则|f(x)|在x=x0连续,即②正确. 在x=0间断,但f2(x)=1在x=0。连续.③也是错的,例如
在x=0间断,但f2(x)=1在x=0。连续.③也是错的,例如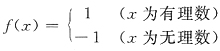 ,则
,则 不存在(易构造两个积分和有不同的极限),但|f(x)|=1在[a,b]可积.因此,只能是②,④正确,选C.
不存在(易构造两个积分和有不同的极限),但|f(x)|=1在[a,b]可积.因此,只能是②,④正确,选C.

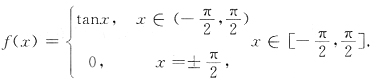

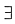 定积分的必要条件是f(x)在[a,b]有界.因此,若f(x)在[a,b]无界,则f(x)在[a,b]不
定积分的必要条件是f(x)在[a,b]有界.因此,若f(x)在[a,b]无界,则f(x)在[a,b]不 定积分.
定积分. 无界
无界 在
在 不
不 定积分.选C.
定积分.选C. A,B,D函数在指定区间可积.因此选C.
A,B,D函数在指定区间可积.因此选C.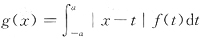 ,则在[-a,a]上
,则在[-a,a]上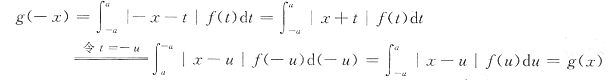


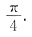









 为奇函数
为奇函数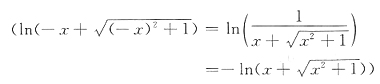
 为偶函数
为偶函数





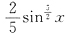 仅在
仅在 上是被积函数的原函数,在
上是被积函数的原函数,在 上的原函数是
上的原函数是 .因此这里的作法是错误的.
.因此这里的作法是错误的. 在x=0无定义,在[-1,1]上无界,不存在定积分,这里错误地应用了牛顿—莱布尼兹公式.
在x=0无定义,在[-1,1]上无界,不存在定积分,这里错误地应用了牛顿—莱布尼兹公式. 不是整个区间[0,π]上的原函数,它在
不是整个区间[0,π]上的原函数,它在 无定义,只是
无定义,只是 与
与 上的原函数,不能在[0,π]上用牛顿—莱布尼兹公式.
上的原函数,不能在[0,π]上用牛顿—莱布尼兹公式. 在x=0无定义,可任意补充定义f(0)后,
在x=0无定义,可任意补充定义f(0)后, 仍不是f(x)在整个区间[-1,1]上的原函数,因为它在x=0无定义,因此不能在[-1,1]上用牛顿—莱布尼兹公式.
仍不是f(x)在整个区间[-1,1]上的原函数,因为它在x=0无定义,因此不能在[-1,1]上用牛顿—莱布尼兹公式.



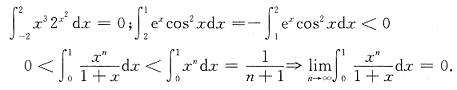






 ,被积函数以π为周期,由周期函数的积分性质
,被积函数以π为周期,由周期函数的积分性质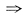

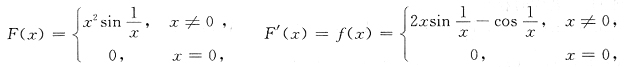
 数F(x),它不是初等函数
数F(x),它不是初等函数 F(z)+f(x)不是初等函数,因此不选D.
F(z)+f(x)不是初等函数,因此不选D. 则在区间(-1,1)上
则在区间(-1,1)上 ,在(-1,0)的原函数为sinx+C2,在x=0处该原函数必连续:
,在(-1,0)的原函数为sinx+C2,在x=0处该原函数必连续: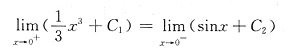
 C1=C2.若f(x)在(-1,1)存在原函数则应是
C1=C2.若f(x)在(-1,1)存在原函数则应是

 f(x)在(-1,1)不存在原函数.选D.
f(x)在(-1,1)不存在原函数.选D.