选择题1. 已知α
1,α
2是非齐次线性方程组Ax=b的两个不同的解,那么
α
1-α
2,3α
1-α
2,
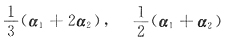
中,仍是线性方程组Ax=b特解的共有
A B C D
B
[解析] 由于Aα
1=b,Aα
2=b,那么
A(3α
1-2α
2)=3Aα
1-2Aα
2=3b-2b=b,
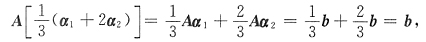
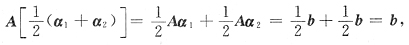
可知3α
1-2α
2,
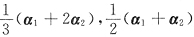
均是Ax=b的解.
而A(α
1-α
2)=Aα
1-Aα
2=b-b=0,所以α
1-α
2是Ax=0的解,不是Ax=b的解,故应选B.
2. 已知α
1,α
2,α
3是非齐次线性方程组Ax=b的三个不同的解,那么下列向量
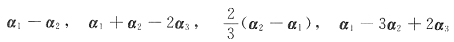
中是导出组Ax=0解的向量共有
A B C D
A
[解析] 由Aα
i=b(i=1,2,3)有
A(α
1-α
2)=Aα
1-Aα
2=b-b=0
A(α
1+α
2-2α
3)=Aα
1+Aα
2-2Aα
3=b+b-2b=0
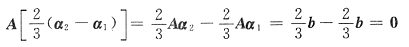
A(α
1-3α
2+2α
3)=Aα
1-3Aα
2+2Aα
3=b-3b+2b=0
所以,α
1-α
2,α
1+α
2-2α
3,
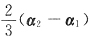
,α
1-3α
2+2α
3均是齐次方程组Ax=0的解.
4. 去看待已知α
1=(1,1,-1)
T,α
2=(1,2,0)
T是齐次方程组Ax=0的基础解系,那么下列向量中Ax=0的解向量是
- A.(1,-1,3)T.
- B.(2,1,-3)T.
- C.(2,2,-5)T.
- D.(2,-2,6)T.
A B C D
B
[解析] 记选项A,B,C,D中向量分别是ξ
1,ξ
2,ξ
3,ξ
4,因ξ
1,ξ
4成比例,如果A是Ax=0的解,则D必是Ax=0的解.因此A、D均不是Ax=0的解.
由于α
1,α
2是Ax=0的基础解系,那么α
1,α
2可表示Ax=0的任何一个解ξ,亦即方程组x
1α
1+x
2α
2=ξ必有解.因为

可见第2个方程组无解,即ξ
3=(2,2,-5)
T不能由α
1,α
2线性表出.故C不成立,应选B.
5. 已知α
1,α
2,α
3是线性非齐次方程组Ax=b三个解向量.则下列向量中仍是Ax=b的解是
A.α
1-α
2-α
3.
B.aα
1+(1-a)α
2-α
3.
C.

D.aα
1-2α
2-3aα
3.
A B C D
C
[解析] 因Aα
i=b,i=1,2,3,故
A项A(α
1-α
2-α
3)=b-b-b=-b≠b.
B项A(aα
1+(1-a)α
2-α
3)=ab+(1-a)b-b-0≠b.
C项
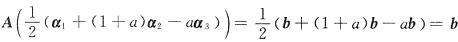
.
D项A(aα
1-2α
2-3aα
3)=ab-2b-3ab=-2(1+a)b≠b.
故应选C.
6. 设η
1,η
2,η
3,η
4是齐次线性方程组Ax=0的基础解系,则Ax=0的基础解系还可以是
- A.η1-η2,η2+η3,η3-η4,η4+η1.
- B.η1+η2,η2+η3+η4,η1-η2+η3.
- C.η1-η2,η2+η3,η3+η4,η4+η1.
- D.η1-η2,η2-η3,η3+η4,η4+η1.
A B C D
D
[解析] 由已知条件知Ax=0的基础解系由四个线性无关的解向量所构成.现在B中仅三个解向量,个数不合要求故B不是基础解系.
A和C中,都有四个解向量,但因为
(η
1-η
2)+(η
2+η
3)-(η
3-η
4)-(η
4+η
1)=0
(η
1+η
2)-(η
2+η
3)+(η
3-η
4)-(η
4+η
1)=0说明A、C中的解向量组均线性相关,因而A、C也均不是基础解系.
用排除法可知D入选.或者盲接地,由
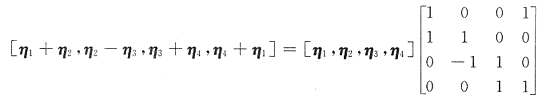
因为
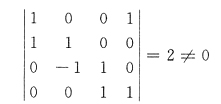
知η
1+η
2,η
2-η
3,η
3+η
4,η
4+η
1线性无关,又因η
1+η
2,η
2-η
3,η
3+η
4,η
4+η
1均是Ax=0的解.且解向量个数为4,所以D是基础解系.
7. 设A是m×n矩阵,A
T是A的转置,若η
1,η
2,…,η
s是齐次方程组A
Tx=0的基础解系,则秩r(A)=
A B C D
C
[解析] 由于A是m×n矩阵,知AT是n×m矩阵,那么ATx=0是n个方程m个未知数的齐次线性方程组,从而m-r(AT)=t.又因r(A)=r(AT),所以r(A)=m-t,即应当选C.
8. 要使α
1=(2,1,1)
T,α
2=(1,-2,-1)
T都是齐次线性方程组Ax=0的解,只要系数矩阵A为
A.

B.
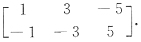
C.
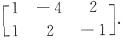
D.
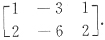
A B C D
B
[解析] 因为α1、α2线性无关,所以Ax=0至少有两个线性无关的解,故
n-r(A)≥2 即r(A)≤3-2=1
因此排除A、C
对于B和D,因为α2不是方程组D的解,因此排除D.故应选B.
12. 设Ax=b有通解k
1ξ
1+k
2ξ
2+η=k
1(1,0,1)
T+k
2(-1,3,2)
T.则下列向量中不是Ax=b的解向量的是
- A.α1=(3,-5,-4)T.
- B.α2=(0,4,2)T.
- C.α3=(3,-2,-1)T.
- D.α4=(3,1,-1)T.
A B C D
D
[解析] 若α
i是Ax=b的解,α
i∈k
1ξ
1+k
2ξ
2+η,,即方程组ξ
1x
1+ξ
2x
2+η=α
i有解.
即ξ
1x
1+ξ
2x
2+η=α
i-η有解.
将ξ
1,ξ
2,α
1-η,α
2-η,α
3-η,α
4-η,合并成矩阵,并作初等行变换,得

显然α
4-η不能由ξ
1,ξ
2线性表出,即α
4不包含于k
1ξ
1+k
2ξ
2+η之中,应选D.
14. 设α
1,α
2,α
3,α
4,α
5都是四维列向量,A=[α
1,α
2,α
3,α
4],非齐次线性方程组Ax=α
5有通解kξ+η=k(1,-1,2,0)
T+(2,1,0,1)
T,则下列关系式中不确的是
- A.2α1+α2+α4-α5=0.
- B.α5-α4-2α3-3α1=0.
- C.α1-α2+2α3-α5=0.
- D.α5-α4+4α3-3α2=0.
A B C D
C
[解析] 方程组有通解kξ+η知
α
5=[α
1,α
2,α
3,α
4][kξ+η]
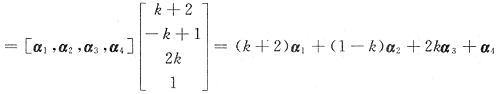
即α
5-(k+2)α
1-(1-k)α
2-2kα
3-α
4=0,其中k是任意常数,即α
1,α
2,α
3,α
4,α
5线性相关,上式线性组合为零中不能没有α
4,选项C中没有α
4,故C不正确.故应选C
当k=0时A成立.
k=1时B成立.
k=-2时D成立.
故A、B、D均是正确的.
15. 已知方程组
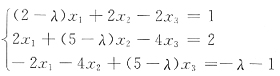
有两个不同的解,则λ=
A B C D
C
[解析] 线性方程组Ax=b有两个不同的解
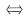
Ax=b有无穷多解
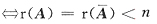
.由于本题的系数矩阵比较复杂,故可以由|A|=0来排查.因为

所以本题中方程组有无穷多解的必要条件是|A|=0,故可排除A与D.
至于λ=1,还是λ=10?可以对增广矩阵代入特殊值后消元处理.例如,把λ=1代人原方程组,有
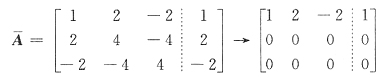
因为
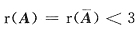
,故知A一1时方程组有无穷多解,即选C.
16. 设A为秩是r的m×n矩阵,非齐次线性方程组Ax=b有解的充分条件是
A B C D
A
[解析] 因为A是m×n矩阵,r(A)=m说明A的行向量组线性无关,那么其延伸组必线性无关,故增广矩阵(A,b)的m个行向量也必线性无关.因此,
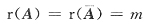
,即方程组Ax=b必有解.但方程组有解时,并不要求秩必为优.所以A是充分条件.那么B、C、D错在何处?
当m=n时,A是秩为r的n阶矩阵,由于增广矩阵的秩不能保证必是r,因此推导不出方程组必有解;
当r(A)=n时,增广矩阵的秩
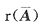
有可能是n+1,因此不能保证Ax=b必有解.(注意A是m×n矩阵,m有可能大于n)你能举个反例吗?
当方程个数小于未知数个数时,Ax=b是否有解仍是不确定的.所以B、C、D均不是方程组有解的充分条件.
17. 设A为m×n矩阵,下列命题中正确的是
- A.若A中有n阶子式不为零,则Ax=0仅有零解.
- B.若A中有n阶子式不为零,则Ax=b必有唯一解.
- C.若A中有m阶子式不为零,则Ax=0仅有零解.
- D.若A中有m阶子式不为零,则Ax=b必有唯一解.
A B C D
A
[解析] A是m×n矩阵,若A中有n阶子式不为零,而A中又不存在n+1阶子式,故必有r(A)=n.同理,若A中有m阶子式不为零,则必有r(A)=m,本题就是考查秩与方程组解之间的关系.
对于A,因为r(A)=n,而Ax=0是n个未知数的齐次方程组,所以Ax=0必只有零解.即A正确.
关于B,当r(A)=n时,增广矩阵A的秩有可能是n+1,所以Ax=b可能无解.即B不正确.为此,请思考下例
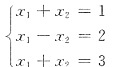
有r(A)=2,
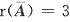
,方程组无解.
至于C和D,r(A)=m说明A的行向量组线性无关,那么其延伸组必线性无关,所以
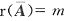
.因此,方程组Ax=b必有解.但是否必有唯一解?Ax=0是否只有零解都是不确定的.例如,
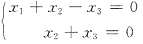
有非零解
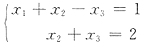
有无穷多解
仅当m=n时,C、D才正确.
18. 已知4阶方阵A=[α
1,α
2,α
3,α
4],α
1,α
2,α
3,α
4均为四维列向量,其中α
1,α
2线性无关,若α
1+2α
2-α
3=β,α
1+α
2+α
3+α
4=β,2α
1+3α
2+α
3+2α
4=β,k
1,k
2为任意常数,那么Ax=β的通解为
A.
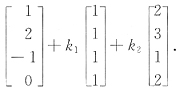
B.
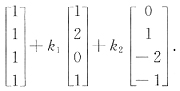
C.
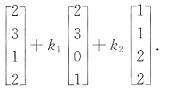
D.
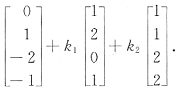
A B C D
B
[解析] 由α
1+2α
2-α
3=β知

即γ
1=(1,2,-1,0)
T是Ax=β的解.同理γ
2=(1,1,1,1)
T,γ
3=(2,3,1,2)
T也均是Ax=β的解.那么
η
1=γ
1-γ
2=(0,1,-2,-1)
T ,η
2=γ
3-γ
2=(1,2,0,1)
T是导出组Ax=0的解,并且它们线性无关.于是Ax=0至少有两个线性无关的解向量,有n-r(A)≥2,即r(A)≤2,又因为α
1、α
2线性无关,有r(A)=r(α
1,α
2,α
3,α
4)≥2.所以必有r(A)=2,从而n-r(A)=2,因此η
1,η
2就是Ax=0的基础解系,根据解的结构B人选.
19. 设A为n阶矩阵,A
T是A的转置矩阵,对于线性方程组(Ⅰ)Ax=0和(Ⅱ)A
TAx=0,必有
- A.(Ⅰ)的解是(Ⅱ)的解,(Ⅱ)的解也是(Ⅰ)的解.
- B.(Ⅰ)的解是(Ⅱ)的解,(Ⅱ)的解不是(Ⅰ)的解.
- C.(Ⅱ)的解是(Ⅰ)的解,(Ⅰ)的解不是(Ⅱ)的解.
- D.(Ⅱ)的解不是(Ⅰ)的解,(Ⅰ)的解也不是(Ⅱ)的解.
A B C D
A
[解析] 如果α是(Ⅰ)的解,有Aα=0,可得
A
TAα=A
T(Aα)=A
T0=0
即α是(Ⅱ)的解.故(Ⅰ)的解必是(Ⅱ)的解.
反之,若α是(Ⅱ)的解,有A
TAα=0,用α
T左乘可得
(Aα)
T(Aα)=(α
TA
T)(Aα)=α
T(A
TAα)=α
T0=0
若设Aα=(b
1,b
2,…,b
n)
T,那么
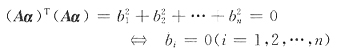
即Aα=0.亦即α是(Ⅰ)的解.因此(Ⅱ)的解也必是(Ⅰ)的解.所以应选A.
21. 设A是n阶矩阵,对于齐次线性方程组(Ⅰ)A
nx=0和(Ⅱ)A
n+1x=0,现有四个命题
(1)(Ⅰ)的解必是(Ⅱ)的解. (2)(Ⅱ)的解必是(Ⅰ)的解.
(3)(Ⅰ)的解不是(Ⅱ)的解. (4)(Ⅱ)的解不是(Ⅰ)的解.
以上命题中正确的是
- A.(1)(2)
- B.(1)(4)
- C.(3)(4)
- D.(2)(3)
A B C D
A
[解析] 若Anα=0,则An+1α=A(Anα)=A0=0,即若α是(Ⅰ)的解,则α必是(Ⅱ)的解,可见命题(1)正确.
下面的问题是选A还是选B?即(2)与(4)哪一个命题正确?
如果An+1α=0,而Anα≠0,那么对于向量组α,Aα,A2α,…,Anα,一方面有:
若kα+k1Aα+k2A2α+…+knAnα=0,用An左乘上式的两边,并把An+1α=0,An+2α=0,……代人,得kAnα=0,
由于Anα≠0而知必有k=0.类似地用An-1左乘可得k1=0,……
因此,α,Aα,A2α,…,Anα线性无关.但另一方面,这是n+1个n维向量它们必然线性相关,两者矛盾.故An+1α=0时,必有Anα=0,即(Ⅱ)的解必是(Ⅰ)的解.因此命题(2)正确.
故命题(1),(2)正确,即Anx=0和An+1x=0也是同解方程,应选A.
22. 设矩阵A=
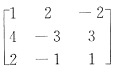
,那么矩阵A的三个特征值是
- A.1,0,-2.
- B.1,1,-3.
- C.3,0,-2.
- D.2,0,-3.
A B C D
D
[解析] 由特征值的性质:
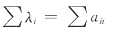
现在
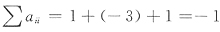
,故可排除C.
显然,矩阵A中第2、第3两列成比例,易知行列式|A|=0,故λ=0必是A的特征值,因此可排除B.
对于A和D的选择,若选项A正确,则A应有λ=1.但说明λ=1不是矩阵A的特征值.故可排除A,由排除法知应选D.
23. 已知A是4阶矩阵,A*是A的伴随矩阵,若A*的特征值是1,-1,2,4,那么不可逆矩阵是
- A.A-E.
- B.2A-E.
- C.A+2E.
- D.A-4E.
A B C D
C
[解析] 根据
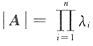
,可知A可逆的充分必要条件是λ
i≠0(i=1,2,…,n)
法一 由A*的特征值是1,-1,2,4知|A*|=-8,又因|A*|=|A|
n-1而知|A|
3=-8,于是|A|=-2,故A的特征值λ≠0,则A*的特征值
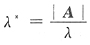
,从而
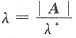
,故,矩阵A的特征值是:
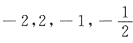
.
因此,A-E的特征值是-3,1,-2,
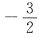
,2A-E的特征值-5,3,-3,-2;A-4E的特征值-6,-2,-5,
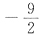
,因为特征值均非0,矩阵A-E,2A-E,A-4E均可逆.
但矩阵A+2E的特征值为0,4,1,
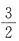
含有0,所以矩阵A+2E不可逆.故应选C.
法二 由法一知|A|=-2,对各选项矩阵左乘A*,对C,有
A*(A+2E)=A*A+2A*=|A|E+2A*=-2E+2A*有特征值0,-4,2,6.
故A*(A+2E)不可逆,因A*可逆,知A+2E不可逆,故应选C.
24. 已知A是n阶可逆矩阵,那么与A有相同特征值的矩阵是
A B C D
A
[解析] 由Aα=λα,α≠0可得到:
A
2α=λ
2α,
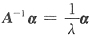
, (A-E)α=(λ-1)α
说明A
2,A
-1,A-E与A的特征值是不一样的(但A的特征向量也是它们的特征向量)由排除法,知应选A.或
由于|λE-AT|=|(λE-A)
T|=|λE-A|
A与A
T有相同的特征多项式,所以A与A
T有相同的特征值.
25. 矩阵
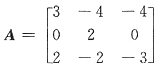
有一个特征向量是
- A.(1,0,-1)T.
- B.(3,3,-6)T.
- C.(4,-1,2)T.
- D.(1,1,-2)T.
A B C D
C
[解析] 若α是A的特征向量,那么kα(k≠0)仍是A的特征向量.因此,如果B正确,必有D正确.所以B、D均不正确,故排除B和D.由Aα=λα,α≠0知α与Aα的对应分量应当成比例.
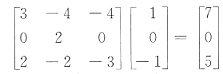
因为(1,0,-1)
T与(7,0,5)
T坐标不成比例,所以(1,0,-1)
T不是A的特征向量,所以A不正确,用排除法可知应选C,或直接逐项验算,其中C
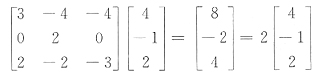
知(4,-1,2)
T是A的特征向量.故应选C.
27. 设A是n阶矩阵,P是n阶可逆矩阵,n维列向量α是矩阵A的属于特征值λ的特征向量,那么在下列矩阵中
(1)A
2 (2)P
-1AP (3)A
T (4)
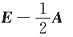
α肯定是其特征向量的矩阵共有
A B C D
B
[解析] 由Aα=λα,α≠0,有A
2α=A(λα)=λAα=λ
2a,α≠0
即α必是A
2属于特征值λ
2的特征向量.
又
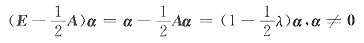
知α必是矩阵

属于特征值
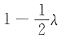
的特征向量.
关于(2)和(3)则不一定成立.这是因为
(P
-1AP)(P
-1α)=P
-1Aα=λP
-1α
按定义,矩阵P
-1AP的特征向量是P
-1α.由于P
-1α与α不一定共线,因此α不一定还是P
-1AP的特征向量,即相似矩阵的特征向量是不一样的.
线性方程组(λE-A)x=0与(λE-A
T)x=0不一定同解,所以α不一定是第二个方程组的解,即α不一定是A
T的特征向量.因此α肯定是其特征向量的矩阵有两个,故应选B.
28. 设A是n阶矩阵,下列命题中正确的是
- A.若α是AT的特征向量,那么α是A的特征向量.
- B.若α是A*的特征向量,那么α是A的特征向量.
- C.若α是A2的特征向量,那么α是A的特征向量.
- D.若α是2A的特征向量,那么α是A的特征向量.
A B C D
D
[解析] 若α是2A的特征向量,即(2A)α=λα,α≠0.
那么
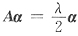
,所以α是矩阵A属于特征值
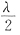
的特征向量.即D正确.由于(λE-A
T)x=0,(λE-A*)x=0,(λE-A
2)x=0分别与(μE-A)x=0不一定有相同的解,所以α不一定是A的特征向量.如取
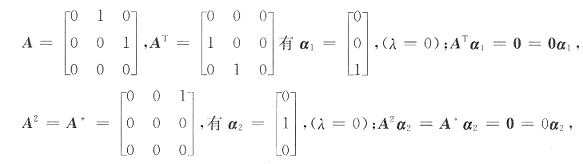
但
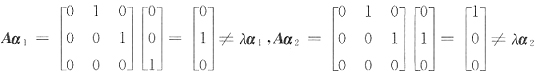
即α
1,α
2均不是A的特征向量.
30. 设A是三阶矩阵,其特征值是1,3,-2,相应的特征向量依次为α
1,α
2,α
3,若P=[α
1,2α
3,-α
2],则P
-1AP=
A.
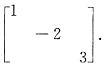
B.

C.
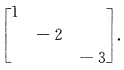
D.
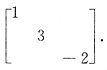
A B C D
A
[解析] 由Aα2=3α2,有A(-α2)=3(-α2),即当α2是矩阵A属于特征值λ=3的特征向量时,-α2仍是矩阵A属于特征值λ=3的特征向量.同理2α3仍是矩阵A属于特征值λ=-2的特征向量.
当P-1AP=A时,P由A的特征向量所构成,A由A的特征值所构成,且P与A的位置是对应一致的.现在,矩阵A的特征值是1,3,-2,故对角矩阵A应当由1,3,-2构成,因此排除B、C.由于2α3是属于λ=-2的特征向量,所以-2在对角矩阵A中应当是第2列,故应选A.
31. 已知
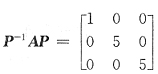
,α
1是矩阵A属于特征值λ=1的特征向量,α
2与α
3是矩阵A属于特征值λ=5的特征向量.那么矩阵P不能是
- A.[α1,-α2,α3].
- B.[α1,α2+α3,α2-2α3].
- C.[α1,α3,α2].
- D.[α1+α2,α1-α2,α3].
A B C D
D
[解析] 若
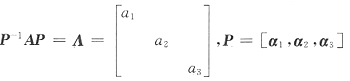
则有AP=PA
即
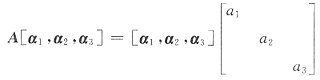
即[Aα
1,Aα
2,Aα
3]=[a
1α
1,a
2α
2,a
3α
3]
可见α
i是矩阵A属于特征值α
i,的特征向量(i=1,2,3),又因矩阵P可逆,因此α
1,α
2,α
3线性无关.
若α是属于特征值λ的特征向量,则-α仍是属于特征值λ的特征向量,故A正确.
若α,β是属于特征值λ的特征向量,则2α+3β,…仍是属于特征值λ的特征向量.本题中,α
2,α
3是属于λ=5的线性无关的特征向量,故α
2+α
3,α2-2α
3仍是λ=5的特征向量,并且α
2+α
3,α
2-2α
3线性无关,故B正确.
关于C,因为α
2,α
3均是λ=5的特征向量,所以α
2与α
3谁在前谁在后均正确.即C正确.
由于α
1,α
2是不同特征值的特征向量,因此α
1+α2,α
1-α
2不再是矩阵A的特征向量,故D错误.
32. 已知矩阵
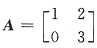
,那么下列矩阵中
(1)

(2)
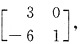
(3)
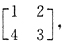
(4)
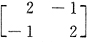
与矩阵A相似的矩阵个数为
A B C D
C
[解析] 二阶矩阵A有两个不相等的特征值1和3,因此
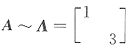
,那么只要和矩阵A有相同的特征值它就一定和∧相似,也就一定与A相似.
(1)与(2)分别是上三角与下三角矩阵,特征值是1和3,所以它们均与A相似,又
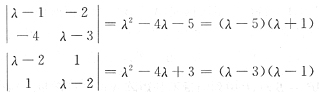
可见(4)亦与A相似.而(3)与A不相似,故与A相似的矩阵有三个,应选C.
33. 下列矩阵中,不能相似对角化的矩阵是
A.

B.

C.

D.

A B C D
D
[解析] A是实对称矩阵,实对称矩阵必可以相似对角化.
B是下三角矩阵,主对角线元素就是矩阵的特征值,因而矩阵有三个不同的特征值,所以矩阵必可以相似对角化.
C是秩为1的矩阵,Ax=0有二个线性无关解,是A的对应于λ=0特征向量.λ=0至少是A的二重特征值,又

,故λ=0是二重特征值A相似于对角阵或由|λE-A|=λ
3-4λ
2,知矩阵的特征值是4,0,0.对于二重根λ=0,由秩
r(0E-A)=r(A)=1
知齐次方程组(0E-A)x=0的基础解系有3-1=2个线性无关的解向量,即λ=0有两个线性无关的特征向量.从而矩阵必可以相似对角化.由排除法,知应选D.或
D是上三角矩阵,主对角线上的元素1,1,-1就是矩阵的特征值,对于二重特征值λ=1,由秩

知齐次方程组(E-A)x=0只有3-2=1个线性无关的解,亦即λ=1只有一个线性无关的特征向量,故矩阵必不能相似对角化.所以应当选D.
34. 下列矩阵中,A和B相似的是
A.
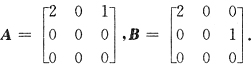
B.
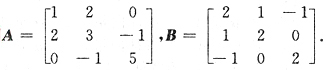
C.
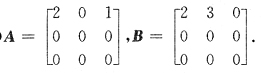
D.
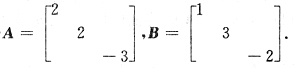
A B C D
C
[解析] 根据A和B相似的必要条件
(1)r(A)=r(B) (2)|A|=|B| (3)λ
A=λ
B (4)
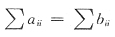
易见A秩不等、B主对角线之和不等、D行列式、或主对角线之和或特征值不等.均不相似所以应选C.实际上,对于C由

知矩阵A的特征值为2,0,0.又因秩r(0E-A)=1,有n-r(0E-A)=2.即齐次方程组(QE-A)x=0有2个线性无关的解,亦即λ=0有两个线性无关的特征向量.从而
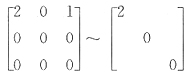
类似地

因此
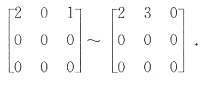
35. 设A是三阶矩阵,B=
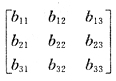
是三阶可逆阵,且
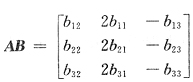
,则A~
A.
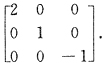
B.

C.

D.
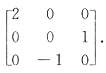
A B C D
C
[解析] 由
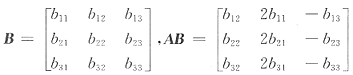
知AB可由B作列变换得到.将B的1、2列互换再将第2列乘2,第3列乘-1,得AB,即

B是可逆阵,两边左乘B
-1,得
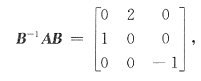
故
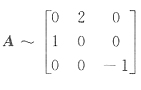
,应选C.
37. 设A、B、C、D都是n阶矩阵,且A~C,B~D,则必有
A.(A+B)~(C+D).
B.
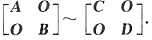
C.AB~CD.
D.
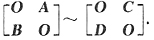
A B C D
B
[解析] A~C,即存在可逆阵P,使P
-1AP=C.B~D,即存在可逆阵Q,使Q
-1BQ=D,故存在可逆阵
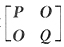
,使得
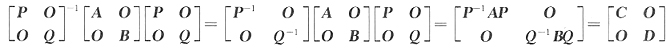
得

,应选B.
A、C、D显然不成立.
38. 已知A是n阶可逆矩阵,若A~B,则下列命题中
(1)AB~BA (2)A
2~B
2 (3)A
-1~B
-1 (4)A
T~B
T 正确的命题共有
A B C D
A
[解析] 由于矩阵A可逆,有
A-1(AB)A=BA
按相似定义知AB~BA.即命题(1)正确.
因为A~B,故存在可逆矩阵P使P-1AP=B,那么
B2=(P-1AP)(P-1AP)=P-1A2P
B-1=(P-1AP)-1=P-1A-1(P-1)-1=P-1A-1P
BT=(P-1AP)T=PTAT(P-1)T=[(P-1)T]-1AT(P-1)T
按相似定义知命题(2)(3)(4)也均正确.故应选A.
41. n阶矩阵A和B具有相同的特征值是A与B相似的
- A.充分必要条件.
- B.必要而非充分条件.
- C.充分而非必要条件.
- D.既非充分也非必要条件.
A B C D
B
[解析] 由A~B,即存在可逆矩阵P使P
-1AP=B知
|λE-B|=|λE-P
-1AP|=|P
-1(λE-A)P|
=|P
-1||λE-A||P|=|λE-A|
即A与B有相同的特征值.
侣当A,B有相同特征值时,A与B不一定相似,例如
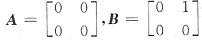
虽然A,B有相同的特征值λ
1=λ
2=0,但由于r(A)≠r(B),A,B不可能相似.所以,相似的必要条件是A.B有相同的特征值.故应选B
43. n阶矩阵A具有n个线性无关的特征向量是A与对角矩阵相似的
- A.充分必要条件.
- B.充分而非必要条件.
- C.必要而非充分条件.
- D.既不充分也不必要条件.
A B C D
A
[解析] 若
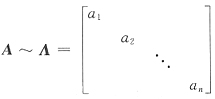
,则有可逆矩阵P使P
-1AP=A或AP=PA令P=[γ
1,γ
2,…,γ
n],即有

从而有
Aγ
i=α
iγ
i i=1,2,…,n
由P可逆,有γ
i≠0,且γ
1,γ
2,…,γ
n线性无关.按定义知γ
1,γ
2,…γ
n是A的n个线性无关的特征向量.
反之,若A有n个线性无关的特征向量α
1,α
2,…,α
n,满足
Aα
i=λ
iα
i,i=1,2,…,n
那么,用分块矩阵有
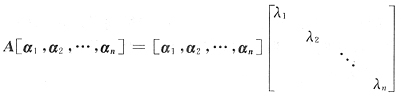
由于矩阵P=[α
1,α
2,…,α
n]可逆.故P
-1AP=A.即A与对角矩阵A相似.
44. 设三阶矩阵A的特征值是0,1,-1,则下列命题中不正确的是
- A.矩阵A-E是不可逆矩阵.
- B.矩阵A+E和对角矩阵相似.
- C.矩阵A属于1与-1的特征向量相互正交.
- D.方程组Ax=0的基础解系由一个向量构成.
A B C D
C
[解析] 因为矩阵A的特征值是0,1,-1,因此矩阵A—E的特征值是-1,0,-2.由于λ=0是矩阵A—E的特征值,所以A—E不可逆.命题A正确.
因为矩阵A+E的特征值是1,2,0,矩阵A+E有三个不同的特征值,所以A+E可以相似对角化.命题B正确.(或由A~∧
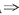
A+E~∧+E而知A+E可相似对角化)
因为矩阵A有三个不同的特征值,知
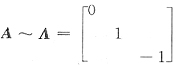
因此,r(A)=r(A)=2,从而齐次方程组Ax=0的基础解系由n-r(A)=3-2=1个解向量构成,即命题D正确.
C的错误在于,若A是实对称矩阵,则不同特征值的特征向量相互正交,而一般n阶矩阵,不同特征值的特征向量仅仅线性无关并不正交,这两个定理的差异要搞清楚.
45. 设
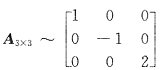
,B=A
3-2A
2-A+5E.刚B=
A B C D
D
[解析] A~∧,故存在可逆阵P,使得P
-1AP=∧,即A=P∧P
-1代入B,得
B=A
3-2A
2-A+5E=(PPP
-1)
3-2(P∧P
-1)
2-P∧P
-1-5PP
-1 =P(∧
3-2∧
2-∧+5E)P
-1 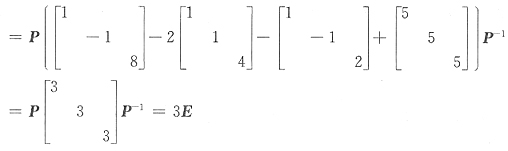
故选D.
46. 二次型
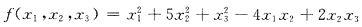
的标准形可以是
A.
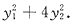
B.
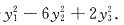
C.
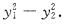
D.
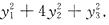
A B C D
A
[解析] 用配方法,有
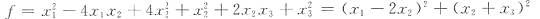
可见二次型的正惯性指数p=2,负惯性指数q=0.与选项A相同,因此,A是二次型的标准形.故应选A.所用坐标变换是:

与
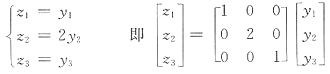
即经坐标变换
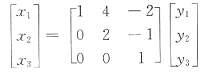
有
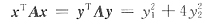
或直接令
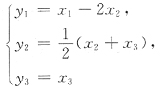
即
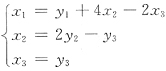
有
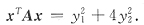
47. 二次型f(x
1,x
2,x
3)=(x
1+x
1)
2+(2x
1+3x
1+x
3)
2=5(x
2+x
3)
2的规范形是
A.
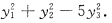
B.
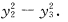
C.
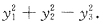
D.
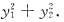
A B C D
B
[解析] 二次型的规范形中,平方项的系数只能是1,-1,0.故应当排除A
只要求出二次型的正、负惯性指数就可以确定二次型的规范形.通常可以求二次型矩阵的特征值或用配方法化二次型为标准形来实现.
二次型f经整理为
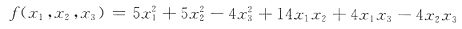
由于
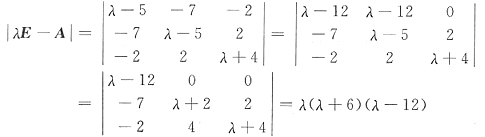
故矩阵A的特征值是12,-6,0.因此二次型正惯性指数p=1,负惯性指数q=1,故应选B.
本题中,若令
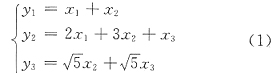
而认为规范形是
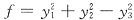
就不正确了.因为行列式

所以上述变换(1)不是坐标变换,(即不是可逆线性变换.)当然
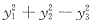
也就不是规范形了.
48. 下列矩阵中,正定矩阵是
A.

B.

C.

D.

A B C D
C
[解析] 二次型正定的必要条件是:a
ii>0.
在D中,由于a
33=0,易知f(0,0,1)=0,与X≠0,X
TAX>0相矛盾.
二次型正定的充分必要条件是顺序主子式全大于零.在A中,二阶主子式
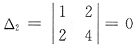
在B中,三阶主子式Δ
3=|A|=-1.
因此A、B、D均不是正定矩阵.故应选C.
51. 设
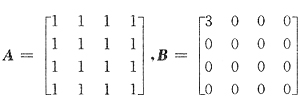
,则A与B有关系
- A.合同且相似.
- B.合同但不相似.
- C.相似但不合同.
- D.不相似也不合同.
A B C D
B
[解析] A,B均是实对称阵,
A有特征值λ
1=λ
2=λ
3=0,λ
4=4
B有特征值μ
1=μ
2=μ
3=0,μ
4=3.
故A,B不相似,但A,B的正惯性指数均为p=1,负惯性指数为0,故A,B合同,应选B.
52. 与二次型
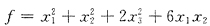
的矩阵A既合同又相似的矩阵是
A.
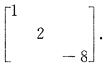
B.
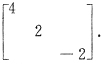
C.
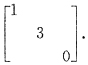
D.
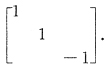
A B C D
B
[解析] 二次型x
TAx经正交变换x=Qy化为新的二次型y
TBy,由于x
TAx=(Qy)
TA(Qy)=y
T(Q
TAQ)y,则有Q
TAQ=B即原二次型矩阵A和新二次型矩阵B合同,又因Q是正交矩阵Q
T=Q
-1,故
QTAQ=Q
-1AQ=B
故A和B又相似
因此在正交变换下,二次型矩阵A与B不仅合同而且相似.
因为两个实对称矩阵相似的充分必要条件是有相同的特征值,现在
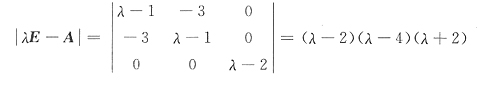
知矩阵A的特征值是2,4,-2.和对角阵B的特征值相同,所以应当选B.
53. 设A,B均n阶实对称矩阵,若A与B合同,则
- A.A与B有相同的特征值.
- B.A与B有相同的秩.
- C.A与B有相同的特征向量.
- D.A与B有相同的行列式.
A B C D
B
[解析] 按定义,若存在可逆矩阵C使C
TAC=B,则称A与B合同.
因为矩阵C可逆,故有r(A)=r(C
TAC)=r(B)即B正确.
注意,若
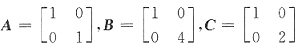
,则有C
TAC=B,即A与B合同.
此时A的特征值是1,1,B的特征值是1,4;(3,2)
T是A的特征向量,但不是B的特征向量;
|A|=1,|B|=4亦不相同.说明A、C、D均不正确.
54. 下列二次型中正定二次型是
- A.f1=(x1-x2)2+(x2-x3)2+(x3-x1)2.
- B.f2=(x1+x2)2+(x2-x3)2+(x3+x1)2.
- C.f3=(x1+x2)2+(x2+x3)2+(x3-x4)2+(x4-x1)2.
- D.f4=(x1+x2)2+(x2+x3)2+(x3+x4)2+(x4-x1)2.
A B C D
D
[解析] 由定义f=x
TAx正定
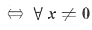
,均有x
TAx>0,反之,若存在X≠0,使得f=x
TAx≤0
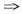
则f或A不正定.
A项因f
1(1,1,1)=0,故A不正定.
B项因f
2(-1,1,1)=0,故B不正定.
C项因f
3(1,-1,1,1)=0,故C不正定.
由排除法,应选D.
55. 设A是n阶实对称矩阵,将A的i列和j列对换得到B,再将B的i行和j行对换得到C,则A与C
- A.等价但不相似.
- B.合同但不相似.
- C.相似但不合同.
- D.等价,合同且相似
A B C D
D
[解析] 将初等行、列变换,用左、右乘初等阵表出,由题设
AE
ij=B,E
ijB=C.
C=E
ijB=E
ijAE
ij 因
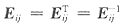
,故
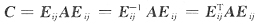
,故即

,C~A,且

,故应洗D.
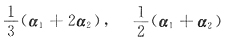
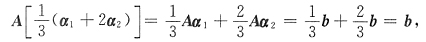
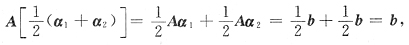
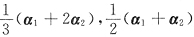 均是Ax=b的解.
均是Ax=b的解.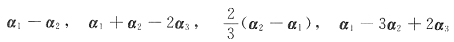
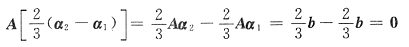
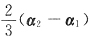 ,α1-3α2+2α3均是齐次方程组Ax=0的解.
,α1-3α2+2α3均是齐次方程组Ax=0的解.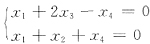 的基础解系是
的基础解系是

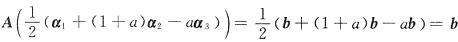 .
.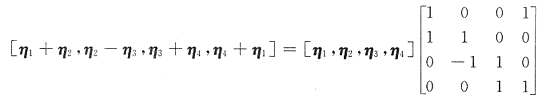
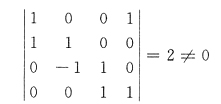

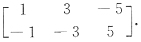
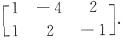
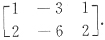
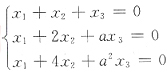 有非零解的
有非零解的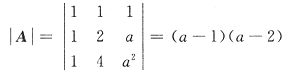
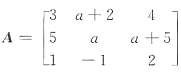 ,若齐次方程组Ax=0的任一非零解均可以用α=(2,0,-1)T线性表出,那么必有a=
,若齐次方程组Ax=0的任一非零解均可以用α=(2,0,-1)T线性表出,那么必有a=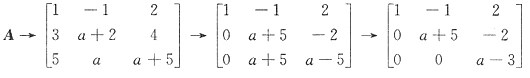

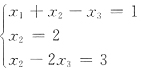
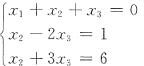
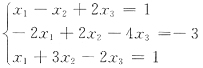
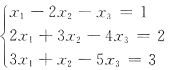
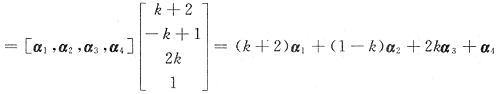
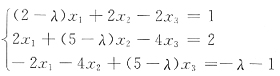
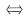 Ax=b有无穷多解
Ax=b有无穷多解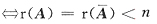 .由于本题的系数矩阵比较复杂,故可以由|A|=0来排查.因为
.由于本题的系数矩阵比较复杂,故可以由|A|=0来排查.因为
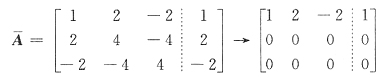
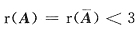 ,故知A一1时方程组有无穷多解,即选C.
,故知A一1时方程组有无穷多解,即选C.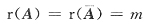 ,即方程组Ax=b必有解.但方程组有解时,并不要求秩必为优.所以A是充分条件.那么B、C、D错在何处?
,即方程组Ax=b必有解.但方程组有解时,并不要求秩必为优.所以A是充分条件.那么B、C、D错在何处?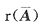 有可能是n+1,因此不能保证Ax=b必有解.(注意A是m×n矩阵,m有可能大于n)你能举个反例吗?
有可能是n+1,因此不能保证Ax=b必有解.(注意A是m×n矩阵,m有可能大于n)你能举个反例吗?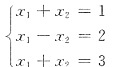
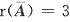 ,方程组无解.
,方程组无解.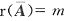 .因此,方程组Ax=b必有解.但是否必有唯一解?Ax=0是否只有零解都是不确定的.例如,
.因此,方程组Ax=b必有解.但是否必有唯一解?Ax=0是否只有零解都是不确定的.例如,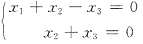 有非零解
有非零解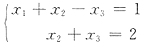 有无穷多解
有无穷多解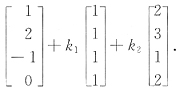

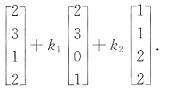
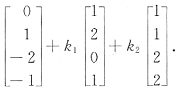

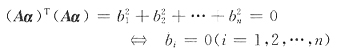
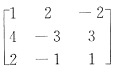 ,那么矩阵A的三个特征值是
,那么矩阵A的三个特征值是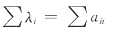
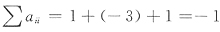 ,故可排除C.
,故可排除C.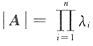 ,可知A可逆的充分必要条件是λi≠0(i=1,2,…,n)
,可知A可逆的充分必要条件是λi≠0(i=1,2,…,n)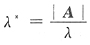 ,从而
,从而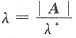 ,故,矩阵A的特征值是:
,故,矩阵A的特征值是: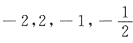 .
.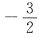 ,2A-E的特征值-5,3,-3,-2;A-4E的特征值-6,-2,-5,
,2A-E的特征值-5,3,-3,-2;A-4E的特征值-6,-2,-5,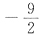 ,因为特征值均非0,矩阵A-E,2A-E,A-4E均可逆.
,因为特征值均非0,矩阵A-E,2A-E,A-4E均可逆. 含有0,所以矩阵A+2E不可逆.故应选C.
含有0,所以矩阵A+2E不可逆.故应选C.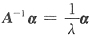 , (A-E)α=(λ-1)α
, (A-E)α=(λ-1)α 有一个特征向量是
有一个特征向量是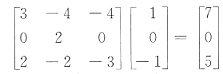
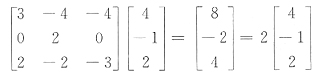
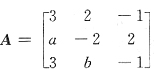 的特征向量,则
的特征向量,则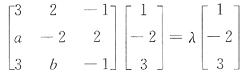
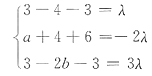
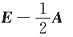
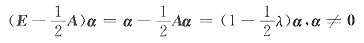
 属于特征值
属于特征值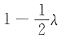 的特征向量.
的特征向量.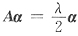 ,所以α是矩阵A属于特征值
,所以α是矩阵A属于特征值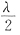 的特征向量.即D正确.由于(λE-AT)x=0,(λE-A*)x=0,(λE-A2)x=0分别与(μE-A)x=0不一定有相同的解,所以α不一定是A的特征向量.如取
的特征向量.即D正确.由于(λE-AT)x=0,(λE-A*)x=0,(λE-A2)x=0分别与(μE-A)x=0不一定有相同的解,所以α不一定是A的特征向量.如取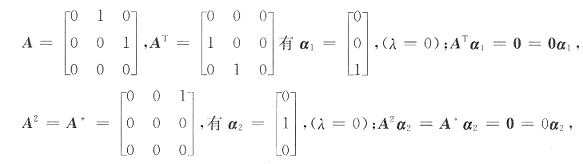
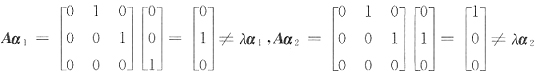
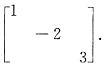

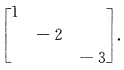
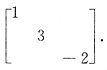
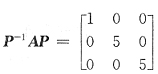 ,α1是矩阵A属于特征值λ=1的特征向量,α2与α3是矩阵A属于特征值λ=5的特征向量.那么矩阵P不能是
,α1是矩阵A属于特征值λ=1的特征向量,α2与α3是矩阵A属于特征值λ=5的特征向量.那么矩阵P不能是
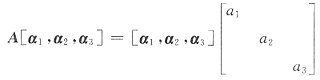
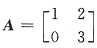 ,那么下列矩阵中
,那么下列矩阵中
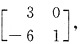
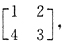
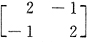
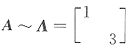 ,那么只要和矩阵A有相同的特征值它就一定和∧相似,也就一定与A相似.
,那么只要和矩阵A有相同的特征值它就一定和∧相似,也就一定与A相似.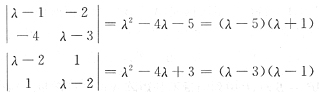




 ,故λ=0是二重特征值A相似于对角阵或由|λE-A|=λ3-4λ2,知矩阵的特征值是4,0,0.对于二重根λ=0,由秩
,故λ=0是二重特征值A相似于对角阵或由|λE-A|=λ3-4λ2,知矩阵的特征值是4,0,0.对于二重根λ=0,由秩
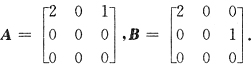
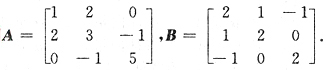
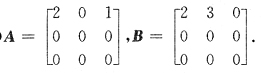
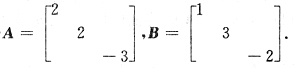
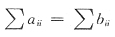

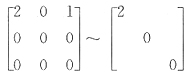


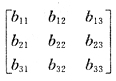 是三阶可逆阵,且
是三阶可逆阵,且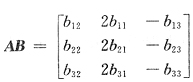 ,则A~
,则A~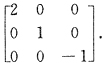


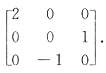
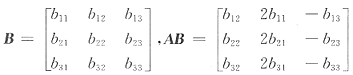 知AB可由B作列变换得到.将B的1、2列互换再将第2列乘2,第3列乘-1,得AB,即
知AB可由B作列变换得到.将B的1、2列互换再将第2列乘2,第3列乘-1,得AB,即
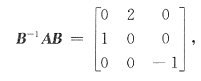
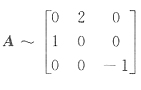 ,应选C.
,应选C.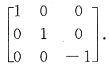



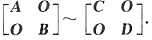
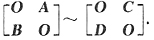
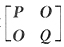 ,使得
,使得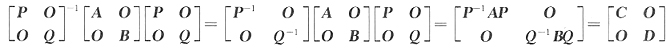
 ,应选B.
,应选B.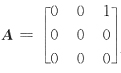 ,r(A)=1,但λ=0是三重特征值.故应选B.
,r(A)=1,但λ=0是三重特征值.故应选B.
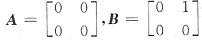
 ,则有可逆矩阵P使P-1AP=A或AP=PA令P=[γ1,γ2,…,γn],即有
,则有可逆矩阵P使P-1AP=A或AP=PA令P=[γ1,γ2,…,γn],即有
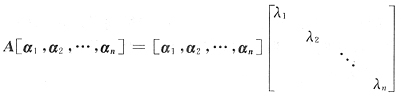
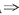 A+E~∧+E而知A+E可相似对角化)
A+E~∧+E而知A+E可相似对角化)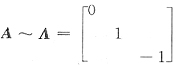
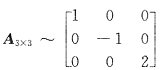 ,B=A3-2A2-A+5E.刚B=
,B=A3-2A2-A+5E.刚B=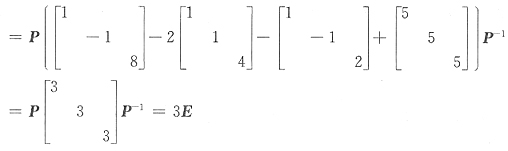
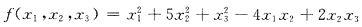 的标准形可以是
的标准形可以是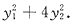
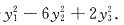
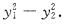
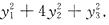
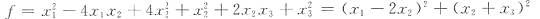



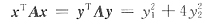
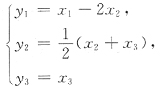
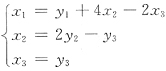 有
有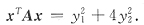
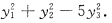
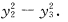
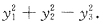
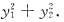
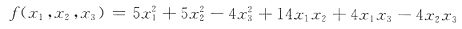
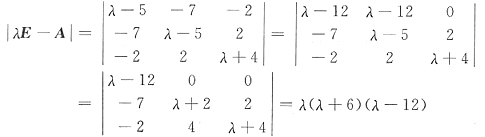
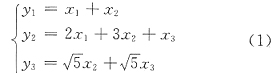
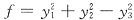 就不正确了.因为行列式
就不正确了.因为行列式
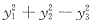 也就不是规范形了.
也就不是规范形了.



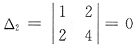
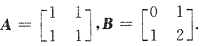
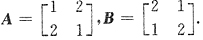
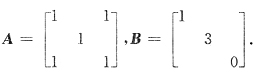
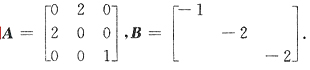
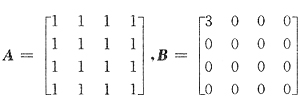 ,则A与B有关系
,则A与B有关系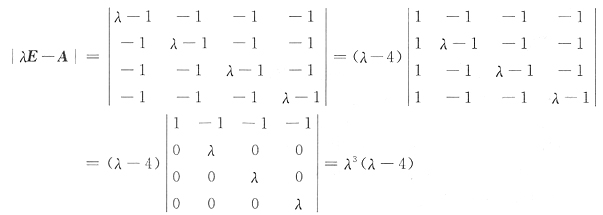
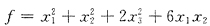 的矩阵A既合同又相似的矩阵是
的矩阵A既合同又相似的矩阵是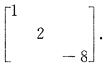
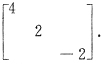
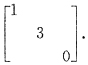
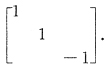
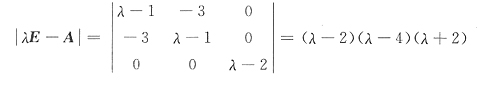
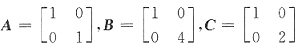 ,则有CTAC=B,即A与B合同.
,则有CTAC=B,即A与B合同.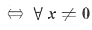 ,均有xTAx>0,反之,若存在X≠0,使得f=xTAx≤0
,均有xTAx>0,反之,若存在X≠0,使得f=xTAx≤0  则f或A不正定.
则f或A不正定.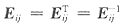 ,故
,故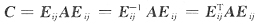 ,故即
,故即 ,C~A,且
,C~A,且 ,故应洗D.
,故应洗D. 