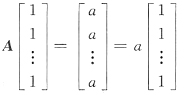
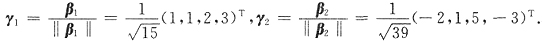填空题1.
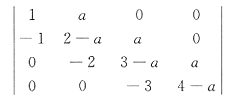
=______.
24
[解析] 在用按行(列)展开公式计算行列式的值时,应先用行列式的性质作恒等变形.以期减少计算量.将a
12=-1,a
23=-2,a
34=-3消为零,行列式变形成上三角行列式,计算得
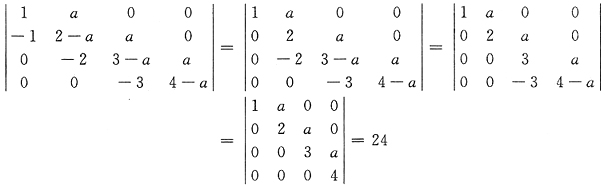
2.
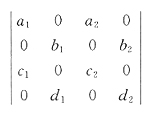
=______.
(a1c2-a2c1)(b1d2-b2d1)
[解析] 本题有较多的0,并有较好的规律性,应当有用拉普拉斯展开式的设想.
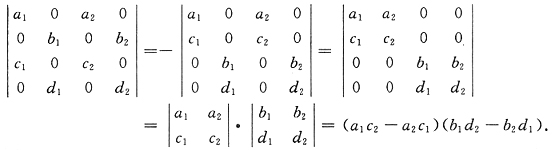
3. 行列式

=______.
120
[解析] 化成范德蒙行列式计算:将行列式第四行逐行加到第一行上,可提出公因子10再将第四行逐行相换至第二行得:

4. 行列式

=______.
4!3!2!(或288)
[解析] 第2、3、4行提出公因子2、3、4,再转置,得范德蒙行列式,直接代入范德蒙行列式的结果得
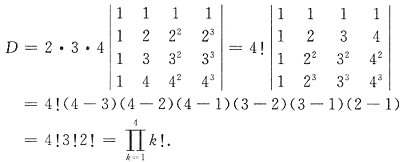
5. 若
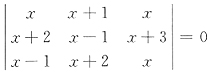
,则x=______.
[解析]
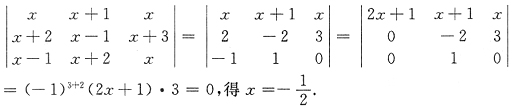
6. 方程
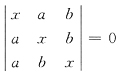
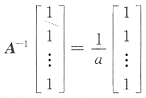
的根是______.
a,b,-(a+b)
[解析] 行列式的展开后是一元三次方程,应有三个根,由观察,当x=a时,一、二行相等,行列式为零,x=a是方程的根.同理x=b也是.(理由?)又行列式每行元素和为相等,且等于x+a+b,将第二、三列加到第一列,并提公因子,得
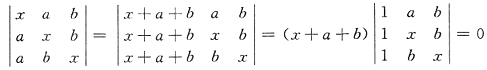
得x=-(a+b).故方程的三个根是a,b,-(a+b).
7. 设
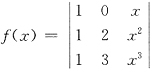
,则f(x+1)-f(x)=______.
6x2
[解析]
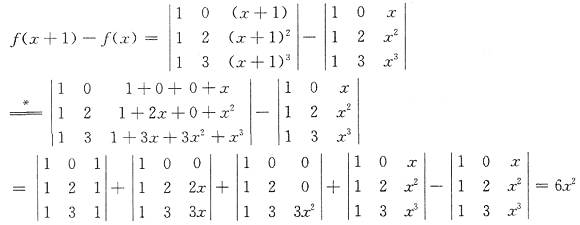
8. 在xoy平面上,平面曲线方程

,则平面曲线与x轴的交点的坐标是______.
(2,0),(3,0)
[解析] 曲线
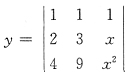
与x轴即y=0的交点为
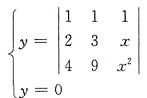
方程右端为范德蒙行列式,
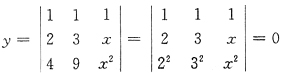
,得x=2,x=3,故曲线与x轴的交点坐标为(2,0),(3,0).
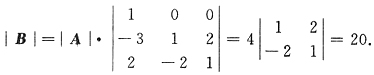
9. 设A=[α
1,α
2,α
3]是3阶矩阵,且|A|=4,若B=[α
1-3α
2+2α
3,α
2-2α
3,2α
2+α
3]则,则|B|=______.
20
[解析] 由行列式性质,将|B|用已知行列式|A|表出.
|B|=|α
1-3α
2+2α
3,α
2-2α
3,2α
2+α
3|
=|α
1-2α
2,α
2-2α
3,2α
2+α
3|
=|α
1-2α
2,α
2-2α
3,5α
3|
=5|α|-2α
2,α
2,α
3|
=5|α
1,α
2,α
3|=20
或者,利用分块矩阵乘法
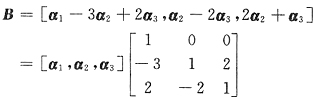
有
10. 设四阶方阵A=[α,γ
2,γ,γ
4],B=[β,γ
2,γ
3,γ
4],其中α,β,γ
2,γ
3,γ
4均为四维列向量,且|A|=4,|B|=-1,则|A-3B|=______.
-56
[解析] 因为
A-3B=[α,γ2,γ3,γ4]-[3β,3γ2,3γ3,3γ4]
=[α-3β,-2γ2,-2γ3,-2γ4]
故有
|A-3B|=|α-3β,-2γ2,-2γ3,-2γ4|
=-8|α-3β,γ2,γ3,γ4|
=-8(|α,γ2,γ3,γ4|-3|β,γ2,γ3,γ4|)
=-8(|A|-3|B|)=-56
11. 设四阶行列式
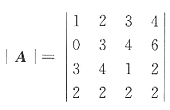
,则A
11+2A
21+A
31+2A
41=______.
-12
[解析] 因为代数余子式A
ij的值与元素a
ij的值无关.本题求第一列元素的代数余子式,故可构造一个新的行列式.把|A|中第1列换为所求和的代数余子式的系数,即

则|A|与|B|的第一列元素的代数余子式A
11,A
21,A
31,A
41是一样的,而对|B|按第1列展开就是
|B|=A
11+2A
21+A
31+2A
41 那么只要计算出行列式|B|的值也就求出本题代数余子式的和.易计算出A
11+2A
21+A
31+2A
41=|B|=-12.
12. 设α=(1,3,-2)
T,β=(2,0,0)
T,A=αβ
T,则A
3=______.
13. 设
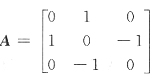
,则A
99=______.
[解析]
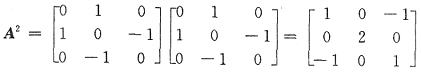
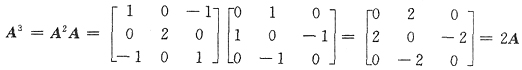
从而有A
5=A
3A
2=2A·A
2=2A
3=2
2A
…………

14. 若
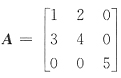
,则矩阵A的伴随矩阵A*=______.
[解析] 按定义,求出行列式|A|的代数余子式,有
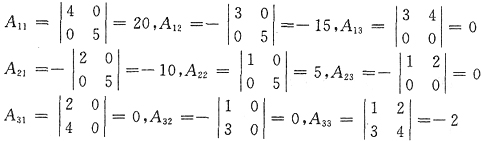
所以
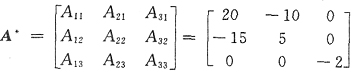
或者,由A
*=|A|A
-1,现在|A|=-10,
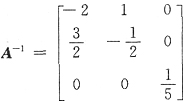
.
而得
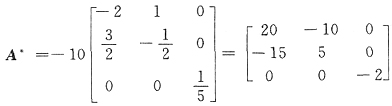
.
15. 已知α
1=(1,0,0)
T,α
2=(1,2,-1)
T,α
3=(-1,1,0)
T,Aα
1=(2,1)
T,Aα
2=(-1,1)
T,Aα
3=(3,-4)
T,则A=______.
[解析] 将Aα
1,Aα
2,Aα
3合并成矩阵,利用分块矩阵,有
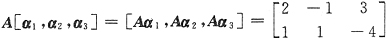
其中
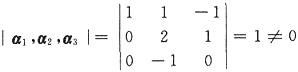
,[α
1,α
2,α
3]可逆,上式两边右乘A
-1 那么
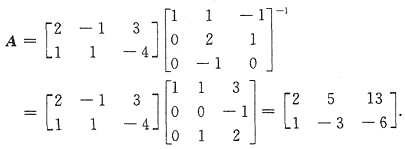
16. 设A=E+αβ
T,其中α,β是n维列向量,且α
Tβ=3,则(A+2E)
-1=______.
[解析] 先求出A满足的关系式,再利用逆矩阵的定义求(A+2E)
-1.因为
A
2=(E+αβ
T)(E+αβ
T)
=E+2αβ
T+αβ
Tαβ
T=E+2αβ
T+α(β
Tα)β
T=E+2αβ
T+α(α
Tβ)β
T =E+5αβ
T=5(E+αβ
T)-4E=5A-4E
即A
2-5A+4E=O
那么(A+2E)(A-7E)+18E=O
得
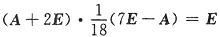
故
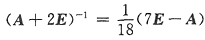
.
17. 设A是n阶矩阵,满足A
5=O,则E-A可逆,R(E-A)
-1=______.
E+A+A2+A3+A4
[解析] A5=O,故-A5=O,两边加E,得
E-A5=E
左边分解因式,有(E-A)(E+A+A2+A3+A4)=E,
故(E-A)-1可逆,且
(E-A)-1=E+A+A2+A3+A4.
18. 设
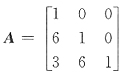
,B=(E-A)(E+2A)
-1,则(B-E)
-1=______.
[解析] (A+B)
-1没有运算法则.应当恒等变形将其化为乘积形式,本题用单位矩阵恒等变形之技巧.
因为B-E=(E-A)(E+2A)
-1-(E+2A)(E+2A)
-1 =[(E-A)-(E+2A)](E+2A)
-1 =-3A(E+2A)
-1 故
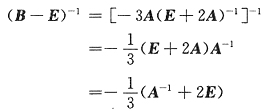
因为
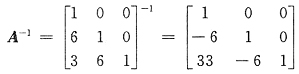
所以
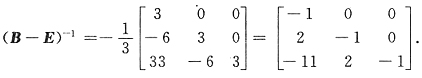
19. 四阶矩阵A和B满足2ABA
-1=AB+6E,若
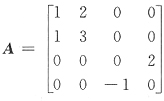
,则B=______.
[解析] 化简矩阵方程,左乘A
-1、右乘A有
2B=BA+6E
于是B(2E-A)=6E
所以
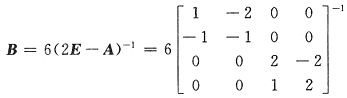
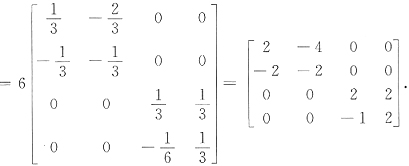
20. 设矩阵A的伴随矩阵
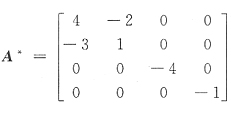
,则A=______.
[解析] 因为AA
*=|A|E,故A=|A|(A
*)
-1,由已知得|A
*|=-8,又|A
*|=|A|
3,得|A|=-2.
又
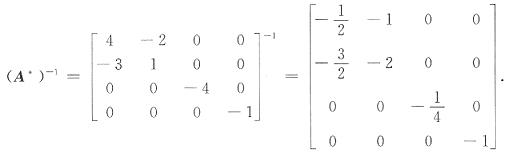
所以
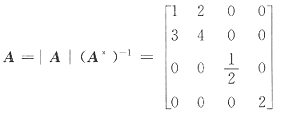
21. 设
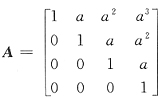
,A
ij是|A|中元素a
ij的代数余子式,则
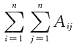
=______.
4-3a
[解析] 若能求得A
*,则A
*的全体元素之和即是|A|的全部代数余子式之和,由公式AA
*=|A|E,故A
*=|A|A
-1.
|A|=1

故
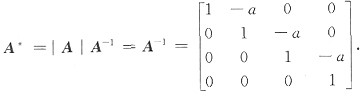
故
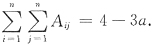
22. 已知三阶矩阵A的逆矩阵为
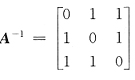
,则矩阵A的伴随矩阵A*的逆矩阵(A*)
-1=______.
[解析] 由AA
*=|A|E,有
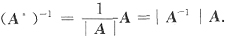
因为(A
-1)
-1=A,求出A
-1的逆矩阵就是求出矩阵A.
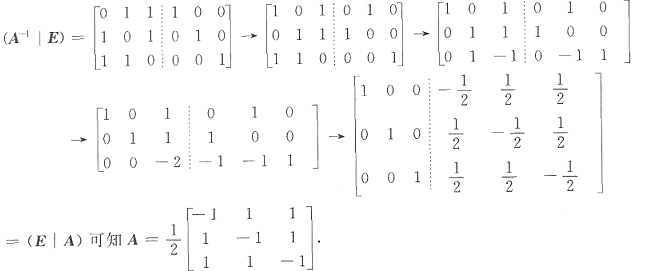
又因|A
-1|=2.故

23. 设A为n阶可逆矩阵,其每一行元素之和都等于a,则A
-1每一行元素之和为______.
[解析] 由于A的每一行元素之和为a,即

即
在等式两边左乘A
-1得

由于A可逆,则a≠0.从而
.故A
-1的每行元素之和为
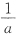
.
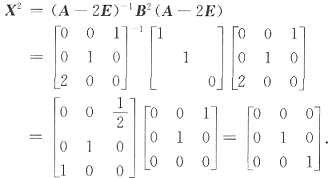
24. 已知
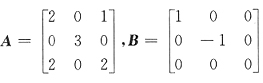
,若X满足AX+2B=BA+2X,那么X
2=______.
[解析] 由已知AX+2B=BA+2X,得
AX-2X=BA-2B,即(A-2E)X=B(A-2E)
由于
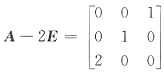
可逆,故X=(A-2E)
-1B(A-2E)
那么
25. 设
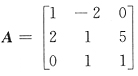
,B是三阶矩阵,则满足AB=O的所有的B=______.
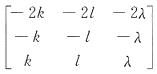
,其中k,l,λ是任意常数
[解析] 将B按列分块,设B=[β
1,β
2,β
3]则
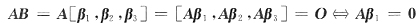
,Aβ
2=0,Aβ
3=0,故β
1,β
2,β
3都是齐次线性方程组Ax=0的解向量.
作齐次线性方程组Ax=0,并求出通解.
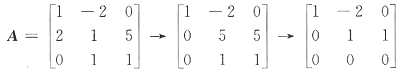
Ax=0有通解k[-2,-1,1]
T,取β
i,i=1,2,3为Ax=0的通解,再合并成B,得
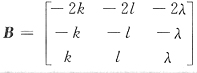
,其中k,l,λ是任意常数.
26. 若
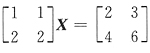
,则X=______.
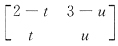
,t、u为任意实数
[解析] 由于矩阵
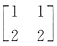
不可逆,故可设
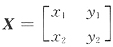
,于是
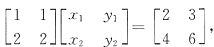
得方程组
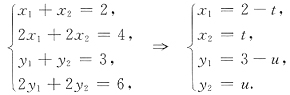
所以

,t,u是任意常数.
27. 已知

,则秩r(AB+2A)=______.
2
[解析] 由AB+2A=A(B+2E),而
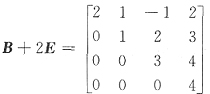
是可逆矩阵,故r(AB+2A)=r(A(B+2E))=r(A)
经初等变换矩阵的秩不变,易见
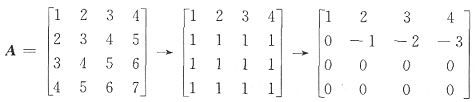
所以r(AB+2A)=2.
28. 设

,A*是A的伴随矩阵,则r(A*)*=______.
0
[解析] 根据
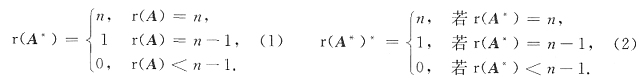
现在n=4,r(A)=3

r(A
*)=1
那么r(A
*)<n-1再利用伴随矩阵秩的关系式(2),就可看出r(A
*)
*=0.
29. 设A是五阶矩阵,A*是A的伴随矩阵,若η
1,η
2是齐次线性方程组Ax=0的两个分量不成比例的解,那么秩r(A*)=______.
0
[解析] 因为η1与η2的分量不成比例,所以η1,η2线性无关.因而齐次方程组Ax=0至少有两个线性无关的解,于是n-r(A)≥2,即有r(A)≤3.
又因为A是五阶矩阵,而r(A)≤3,故|A|中4阶子式必全为0,因此,代数余子式Aij恒为零,从而A*=0,所以秩r(A*)=0.
30. 设
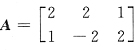
经初等行变换化成3阶梯形矩阵

初等变换过程如下.
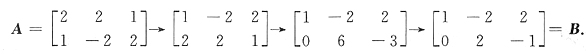
故知有可逆阵P,使得PA=B,其中P=______.
[解析] 初等行变换相当于左乘初等阵,将题设初等行变换的过程用左乘初等阵表出即可
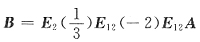
故
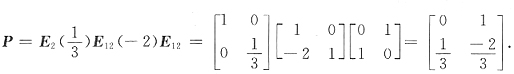
31. 设
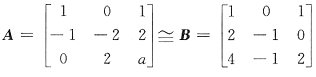
,则a=______.
32. 已知向量组α
1=(1,2,-1,1)
T,α
2=(2,0,t,0)
T,α
3=(0,-4.5,t)
T线性无关,则t的取值范围为______.
(-∞,+∞)
[解析] 由于向量的个数与维数不一样,不能用行列式去分析,而要用齐次方程组只有零解,或矩阵的秩等于n来进行分析.

由于
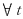
,恒有r(A)=3,所以向量组α
1,α
2,α
3必线性无关.
33. 设n维向量α
1,α
2,α
3满足2α
1-α
2+3α
3=0,β是任意n维向量,若β+α
1,β+α2,αβ+α
3线性相关,则a=______.
[解析] β+α
1,β+α
2,αβ+α
3线性相关,存在不全为零的数k
1,k
2,k
3,使得
k
1(β+α
1)+k
2(β+α
)+k
3(αβ+α
3)=0
整理得(k
1+k
2+k
3a)β+(k
1α
1+k
2α
2+k
3α
3)=0
因已知2α
1-α
2+3α
3=0,且β是任意向量,上式成立,只需取k
1=2,k
2=-1,k
3=3,则有2α
1-α
2+3α
3=0,且令β的系数为0,即k
1+k
2+ak
3-2-1+3a=0,即
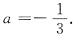
34. 已知α
1,α
2,α
3线性无关,若α
1+2α
2+α
3,α
1+aα
2,3α
2-aα
3线性相关,则a=______.
3或-1
[解析] 因为
α
1+2α
2+α
3,α
1+aα
2,3α
2-aα
3 线性相关,故有不全为0的x
1,x
2,x
3使
x
1(α
1+2α
2+α
3)+x
2(α
1+aα
2)+x
3(3α
2-aα
3)=0
即
(x
1+x
2)α
+(2x
1+ax
2+3x
)α
2+(x
1-αx
3)α
3=0
已知α
1,α
2,α
3线性无关,故必有
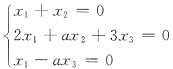
因为x
1,x
2,x
3不全为0,所以上述齐次方程组有非零解.系数行列式必为0,于是
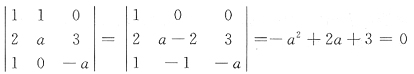
从而a=3或-1.
35. 向量组α
1=(1,-2,0,3)
T,α
2=(2,-5,-3,6)
T,α
3=(0,1,3,0)
T,α
4=(2,-1,4,7)
T的一个极大线性无关组是______
α1,α2,α4(不唯一)
[解析] 列向量作行变换,有
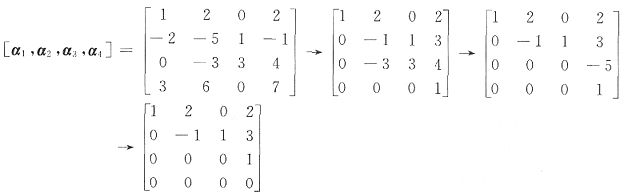
因为矩阵中有3个非零行,所以向量组的秩为3,又因非零行的第一个不等于零的数分别在1,2,4列,所以α
1,α
2,α
4是向量组α
1,α
2,α
3,α
4的一个极大线性无关组.
36. 已知向量β=(1,a,-1)
T可以由α
1=(a+2,7,1)
T,α
2=(1,-1,2)
T线性表出,则a=______.
3或-4
[解析] 因为对任何a,α
1,α
2分量不成比例,故线性无关,所以β可由α
1,α
2线性表出的充分必要条件是α
1,α
2,β线性相关.又因α
1,α
2,β是3个3维向量.故α
1,α
2,β线性相关的充分必要条件是行列式|α
1,α
2,β|=0.
由于
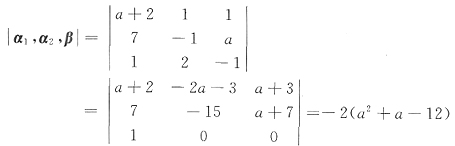
所以a=3或a=-4.
37. 已知α
1=(2,3,3)
T,α
2=(1,0,3)
T,α
3=(3,4,a+2)
T 若β1=(4,-3,15)
T可由α
1,α
2,α
3线性表出,β
2=(-2,-5,a)
T不能由α
1,α
2,α
3线性表出,则a=______.
2
[解析] β
1可由α
1,α
2,α
3线性表出,即方程组x
1α
1+x
2α
2+x
3α
3=β
1有解,β
2不能由α
1,α
2,α
3线性表出,即方程组y
1α
1+y
2α
2+y
3α
3=β
2无解.由于这两个方程组的系数矩阵是一样的,因此可联合起来加减消元.
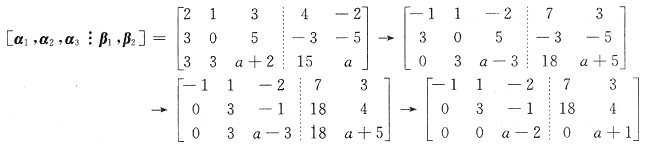
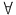
a,方程组
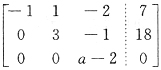
总有解,即β
1必可由α
1,α
2,α
3线性表出.
而方程组
在a=2时元解,即β
2在a=2时不能由α
1,α
2,α
3线性表出.故a=2.
38. 已知α
1=(1,4,2)
T,α
2=(2,7,3)
T,α
3=(0,1,a)
T可以表示任意一个三维向量,则a的取值为______.
a≠1
[解析] 三个3维向量α
1,α
2,α
3可表示任一个3维向量
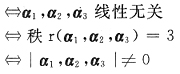
由
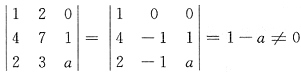
.
所以a≠1.
39. 与α
1=(1,2,3,-1)
T,α
2=(0,1,1,2)
T,α
3=(2,1,3,0)
T都正交的单位向量是______.
[解析] 向量α,β正交
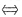
内积α
Tβ=0
设β=(x
1,x
2,x
3,x
4)
T与α
1,α
2,α
3均正交,那么
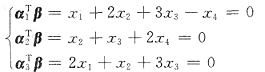
对齐次方程组Ax=0的系数矩阵作初等行变换,有
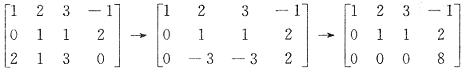
得到基础解系是β=(-1,-1,1,0)
T.将其单位化故即
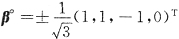
为所求.
40. 向量α
1=(1,1,2,3)
T,α
2=(-1,1,4,-1)
T的Schmidt正交规范化向量组是______.
[解析] 先正交化
β
1=α
1=(1,1,2,3)
T 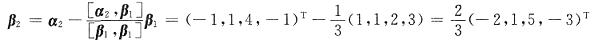
,取分量为整数得β
2=(-2,1,5,-3)
T 再单位化,有
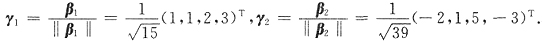
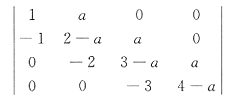 =______.
=______.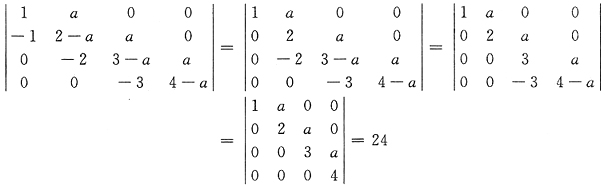
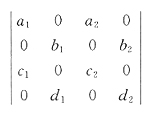 =______.
=______.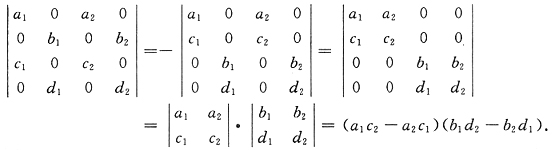
 =______.
=______.
 =______.
=______.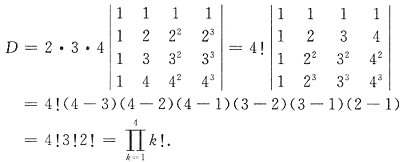
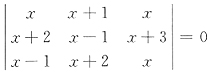 ,则x=______.
,则x=______.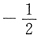
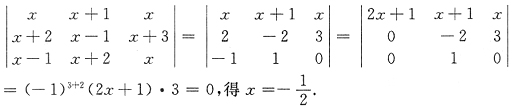
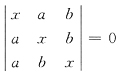 的根是______.
的根是______.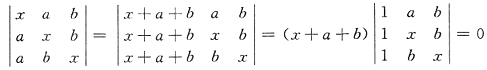
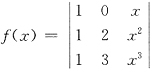 ,则f(x+1)-f(x)=______.
,则f(x+1)-f(x)=______.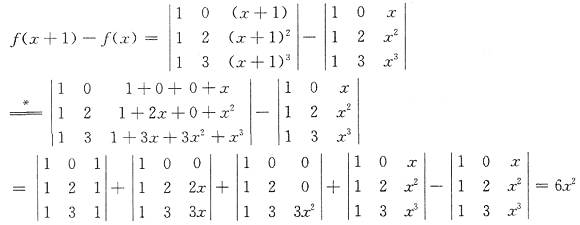
 ,则平面曲线与x轴的交点的坐标是______.
,则平面曲线与x轴的交点的坐标是______.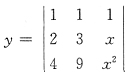 与x轴即y=0的交点为
与x轴即y=0的交点为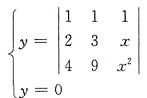
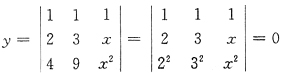 ,得x=2,x=3,故曲线与x轴的交点坐标为(2,0),(3,0).
,得x=2,x=3,故曲线与x轴的交点坐标为(2,0),(3,0).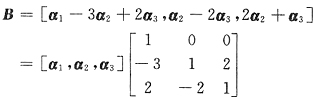

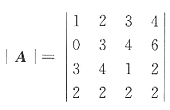 ,则A11+2A21+A31+2A41=______.
,则A11+2A21+A31+2A41=______.

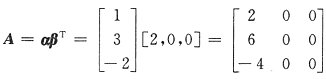
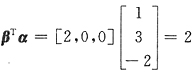
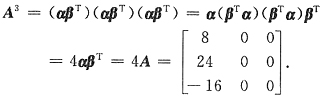
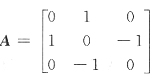 ,则A99=______.
,则A99=______.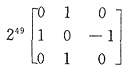
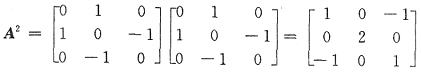
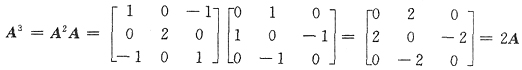

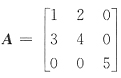 ,则矩阵A的伴随矩阵A*=______.
,则矩阵A的伴随矩阵A*=______.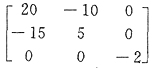
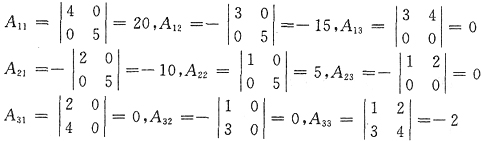
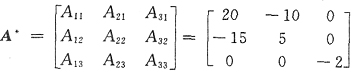
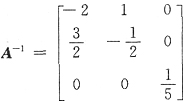 .
.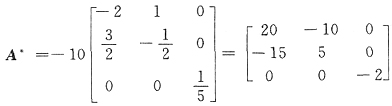 .
.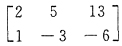
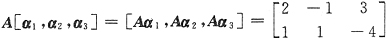
 ,[α1,α2,α3]可逆,上式两边右乘A-1
,[α1,α2,α3]可逆,上式两边右乘A-1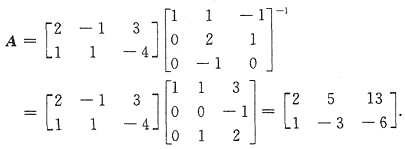
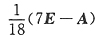
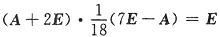
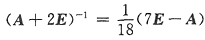 .
.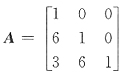 ,B=(E-A)(E+2A)-1,则(B-E)-1=______.
,B=(E-A)(E+2A)-1,则(B-E)-1=______.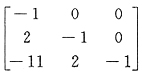
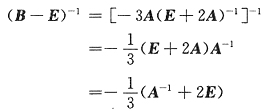
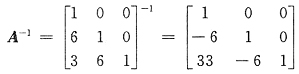
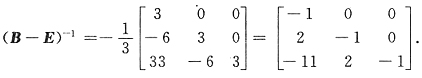
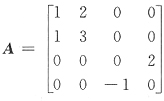 ,则B=______.
,则B=______.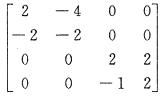
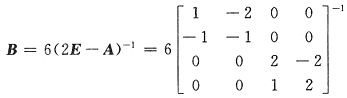
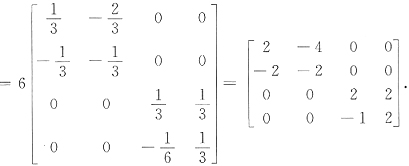
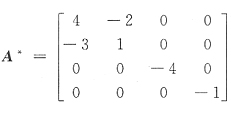 ,则A=______.
,则A=______.
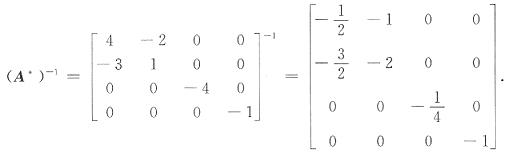
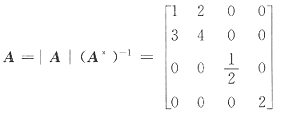
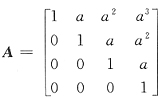 ,Aij是|A|中元素aij的代数余子式,则
,Aij是|A|中元素aij的代数余子式,则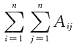 =______.
=______.
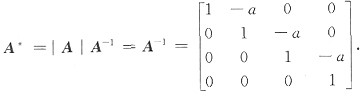
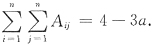
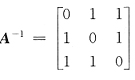 ,则矩阵A的伴随矩阵A*的逆矩阵(A*)-1=______.
,则矩阵A的伴随矩阵A*的逆矩阵(A*)-1=______.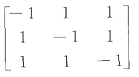
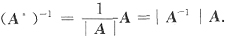


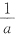



 .故A-1的每行元素之和为
.故A-1的每行元素之和为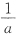 .
.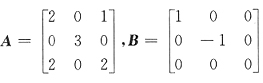 ,若X满足AX+2B=BA+2X,那么X2=______.
,若X满足AX+2B=BA+2X,那么X2=______.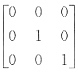
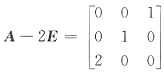 可逆,故X=(A-2E)-1B(A-2E)
可逆,故X=(A-2E)-1B(A-2E)
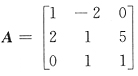 ,B是三阶矩阵,则满足AB=O的所有的B=______.
,B是三阶矩阵,则满足AB=O的所有的B=______.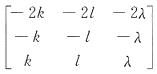 ,其中k,l,λ是任意常数
,其中k,l,λ是任意常数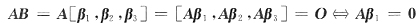 ,Aβ2=0,Aβ3=0,故β1,β2,β3都是齐次线性方程组Ax=0的解向量.
,Aβ2=0,Aβ3=0,故β1,β2,β3都是齐次线性方程组Ax=0的解向量.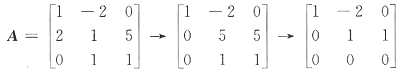
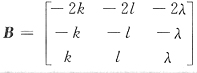 ,其中k,l,λ是任意常数.
,其中k,l,λ是任意常数.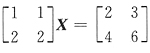 ,则X=______.
,则X=______.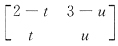 ,t、u为任意实数
,t、u为任意实数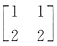 不可逆,故可设
不可逆,故可设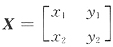 ,于是
,于是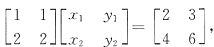
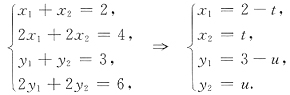
 ,t,u是任意常数.
,t,u是任意常数. ,则秩r(AB+2A)=______.
,则秩r(AB+2A)=______.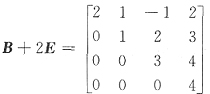

 ,A*是A的伴随矩阵,则r(A*)*=______.
,A*是A的伴随矩阵,则r(A*)*=______.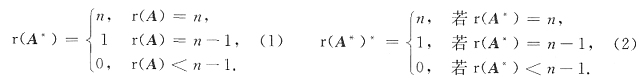
 r(A*)=1
r(A*)=1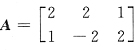 经初等行变换化成3阶梯形矩阵
经初等行变换化成3阶梯形矩阵 初等变换过程如下.
初等变换过程如下.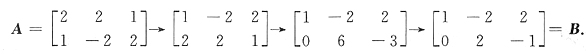
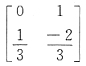
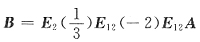
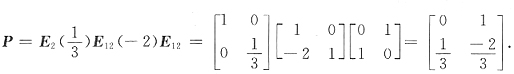
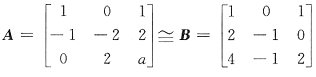 ,则a=______.
,则a=______.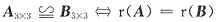
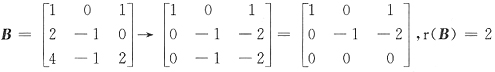


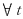 ,恒有r(A)=3,所以向量组α1,α2,α3必线性无关.
,恒有r(A)=3,所以向量组α1,α2,α3必线性无关.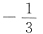
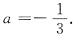
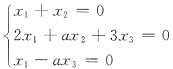
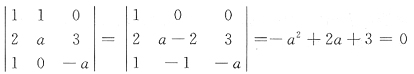

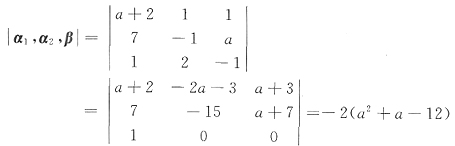
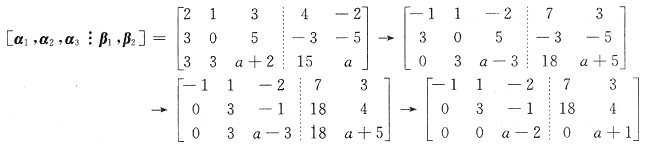
 a,方程组
a,方程组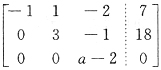 总有解,即β1必可由α1,α2,α3线性表出.
总有解,即β1必可由α1,α2,α3线性表出.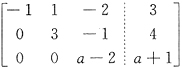 在a=2时元解,即β2在a=2时不能由α1,α2,α3线性表出.故a=2.
在a=2时元解,即β2在a=2时不能由α1,α2,α3线性表出.故a=2.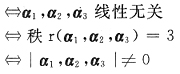
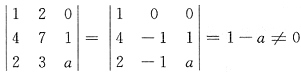 .
.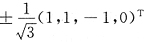
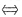 内积αTβ=0
内积αTβ=0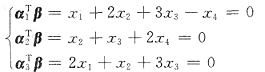
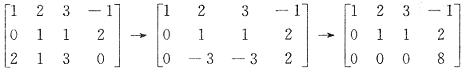
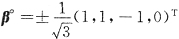 为所求.
为所求.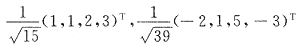
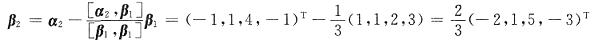 ,取分量为整数得β2=(-2,1,5,-3)T
,取分量为整数得β2=(-2,1,5,-3)T